円筒形のクロスフロー:圧力分布の測定とドラッグ係数の推定
概要
出典:デビッド・グオ、工学・技術・航空学部(CETA)、南ニューハンプシャー大学(SNHU)、マンチェスター、ニューハンプシャー州
円筒形の流れの圧力分布とドラッグ推定値は、何世紀にもわたって調査されてきました。理想的なインビシド電位流れ理論により、円柱の周囲の圧力分布は垂直対称です。円柱の上流および下流の圧力分布も対称であり、ゼロネットドラッグ力をもたらします。しかし、実験結果は、非常に異なる流れパターン、圧力分布、ドラッグ係数をもたらします。これは、理想的なインビシド電位理論が回転不動の流れを前提としているため、流れパターンを決定する際に粘度が考慮または考慮されないためです。これは現実とは大きく異なります。
このデモでは、風洞を利用して指定された対気速度を生成し、24ポートの圧力を持つシリンダーを使用して圧力分布データを収集します。このデモンストレーションでは、円形の円柱の周囲を流れる実際の流体の圧力が、理想化された流体の潜在的な流れに基づく予測結果とどのように異なるかを示します。ドラッグ係数も推定され、予測値と比較されます。
手順
1. シリンダー周辺の圧力分布の測定
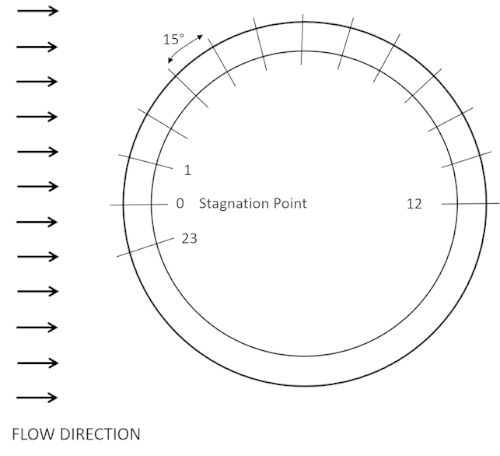
- 風洞のテストセクションの上部カバーを取り外し、ターンテーブルに24の内蔵ポートを備えたクリーンなアルミシリンダー(d =4インチ)を取り付けます(図3)。ポート 0 が上流に向かるようにシリンダを取り付けます (図 4a)。
- 上部カバーを交換し、0~23とラベル付けされた24本の圧力管を、マノメーターパネルの対応するポートに接続します。マノメーターパネルは着色された油で満たされるべきであるが、水中でマークされている必要があります。
- 風洞をオンにし、時速60マイルで走らせる、 24の圧力測定値をすべて記録し、計器を読み取ります。この対気速度では、レイノルズ数は 1.78 x 105です。期待されるフロー パターンを図 2dに示します。
結果
クリーンおよび乱れたシリンダの実験結果を、それぞれ表1および2に示す。データは、図6に示すように、理想的かつ実際の流れのための圧力係数、Cp、対角位置、θのグラフにプロットすることができる。