Flusso cilindrico incrociato: misurazione della distribuzione della pressione e stima dei coefficienti di resistenza
Panoramica
Fonte: David Guo, College of Engineering, Technology, and Aeronautics (CETA), Southern New Hampshire University (SNHU), Manchester, New Hampshire
Le distribuzioni di pressione e le stime di resistenza per il flusso cilindrico incrociato sono state studiate per secoli. Secondo la teoria del flusso potenziale inviscido ideale, la distribuzione della pressione attorno a un cilindro è verticalmente simmetrica. Anche la distribuzione della pressione a monte e a valle del cilindro è simmetrica, il che si traduce in una forza di resistenza netta zero. Tuttavia, i risultati sperimentali producono modelli di flusso, distribuzioni di pressione e coefficienti di resistenza molto diversi. Questo perché la teoria del potenziale inviscido ideale presuppone un flusso irrotazionale, il che significa che la viscosità non viene considerata o presa in considerazione quando si determina il modello di flusso. Questo differisce significativamente dalla realtà.
In questa dimostrazione, una galleria del vento viene utilizzata per generare una velocità dell'aria specificata e un cilindro con 24 porte di pressione viene utilizzato per raccogliere i dati di distribuzione della pressione. Questa dimostrazione illustra come la pressione di un fluido reale che scorre attorno a un cilindro circolare differisca dai risultati previsti in base al flusso potenziale di un fluido idealizzato. Anche il coefficiente di resistenza aerodinamica sarà stimato e confrontato con il valore previsto.
Procedura
1. Misurare la distribuzione della pressione attorno a un cilindro
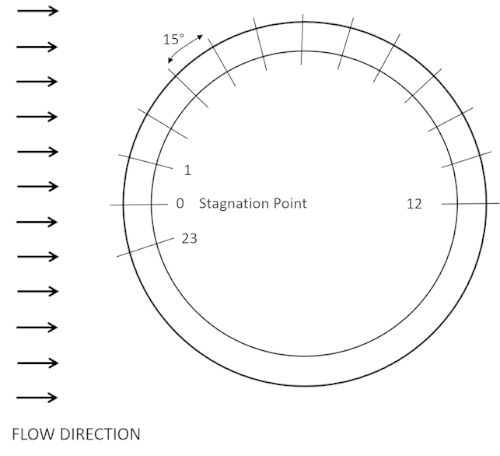
- Rimuovere il coperchio superiore della sezione di prova di una galleria del vento e montare un cilindro di alluminio pulito (d = 4 pollici) con 24 porte integrate su un giradischi (Figura 3). Installare il cilindro in modo che la porta zero sia rivolta a monte (Figura 4a).
- Sostituire il coperchio superiore e collegare i 24 tubi di pressione etichettati 0 - 23
Risultati
I risultati sperimentali per il cilindro pulito e disturbato sono mostrati rispettivamente nelle tabelle 1 e 2. I dati possono essere tracciati in un grafico del coefficiente di pressione, Cp, contro posizione angolare, θ, per il flusso ideale e reale come mostrato in Figura 6.