The rate of a reaction is affected by the concentrations of reactants. Rate laws (differential rate laws) or rate equations are mathematical expressions describing the relationship between the rate of a chemical reaction and the concentration of its reactants.

For example, in a generic reaction aA + bB ⟶ products, where a and b are stoichiometric coefficients, the rate law can be written as:

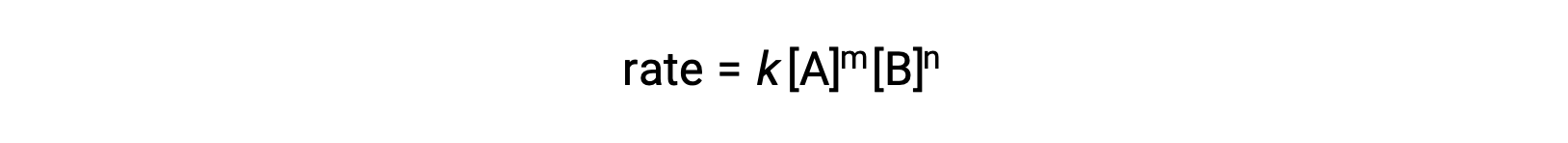
[A] and [B] represent the molar concentrations of reactants, and k is the rate constant, which is specific for a particular reaction at a specific temperature.

The exponents m and n are the reaction orders and are typically positive integers, though they can be fractions, negative, or zero.

The rate constant k and the reaction orders m and n are determined experimentally by observing how the rate of a reaction changes as the concentrations of the reactants are changed. The rate constant k is independent of the reactant concentrations, but varies with temperature.

The reaction orders in a rate law describe the mathematical dependence of the rate on reactant concentrations. Referring to the generic rate law (rate = k[A]^m[B]ⁿ), the reaction is m order with respect to A and n order with respect to B. For example, if m = 1 and n = 2, the reaction is first order in A and second order in B. The overall reaction order is simply the sum of orders for each reactant. For the example rate law here, the reaction is third order overall (1 + 2 = 3).

A common experimental approach to the determination of rate laws is the method of initial rates. This method involves measuring reaction rates for multiple experimental trials carried out using different initial reactant concentrations. Comparing the measured rates for these trials permits determination of the reaction orders and, subsequently, the rate constant, which together are used to formulate a rate law.

Rate laws may exhibit fractional orders for some reactants, and negative reaction orders are sometimes observed when an increase in the concentration of one reactant causes a decrease in reaction rate. It is important to note that rate laws are determined by experiment only and are not reliably predicted by reaction stoichiometry.

The reaction order determines the relationship between the reaction rate and the concentration of reactants or products.

In a zero-order reaction, the concentration of the reactants does not have any effect on the rate of the reaction, which remains constant throughout.
In a first-order reaction, the reaction rate is directly and linearly proportional to the change in reactant concentration. As the reactant concentration decreases, the reaction rate also decreases proportionally.
In second-order or higher-order reactions, the reaction rate is proportional to the exponential value of the reactants. Therefore, as the reaction progresses and the concentration of the reactants decreases, the reaction rate decreases exponentially.

This text is adapted from Openstax, Chemistry 2e, Section 12.3: Rate Laws.