While the differential rate law relates the rate and concentrations of reactants, a second form of rate law called the integrated rate law relates concentrations of reactants and time. Integrated rate laws can be used to determine the amount of reactant or product present after a period of time or to estimate the time required for a reaction to proceed to a certain extent. For example, an integrated rate law helps determine the length of time a radioactive material must be stored for its radioactivity to decay to a safe level.

Using calculus, the differential rate law for a chemical reaction can be integrated with respect to time to give an equation relating the reactant/product amount to the elapsed time of the reaction.

First-Order Reactions

Integration of the rate law for a simple first-order reaction (rate = k[A]) results in an equation describing the variation in reactant concentration with time:

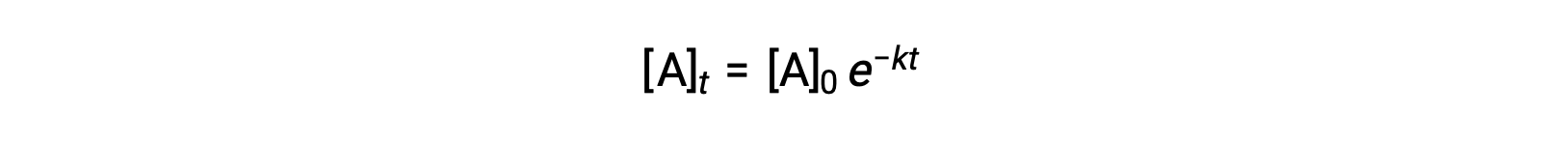
Here, [A]_t is the concentration of A at any time t, [A]₀ is the initial concentration of A, and k is the first-order rate constant. For mathematical convenience, this equation is rearranged to a format showing a linear dependence of concentration on time that takes the form of a straight-line equation (y = mx + b):

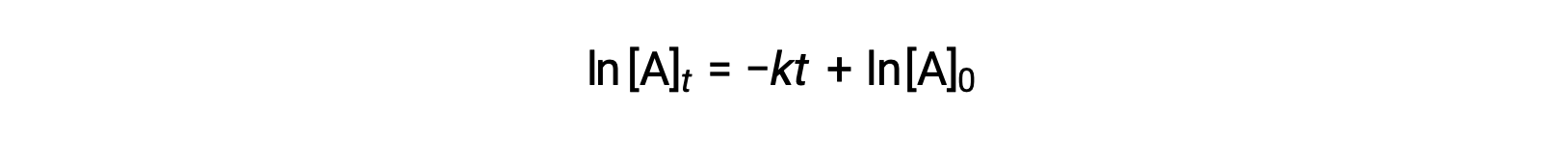
The equation suggests that a plot of ln[A]_t versus t for a first-order reaction is a straight line with a slope of −k and a y-intercept of ln[A]₀. If a set of rate data are plotted in this fashion but do not result in a straight line, the reaction is not first order in A.

Second-Order Reactions

The differential rate law for a simple second-order reaction is rate = k[A]²_, and the integrated rate law is:

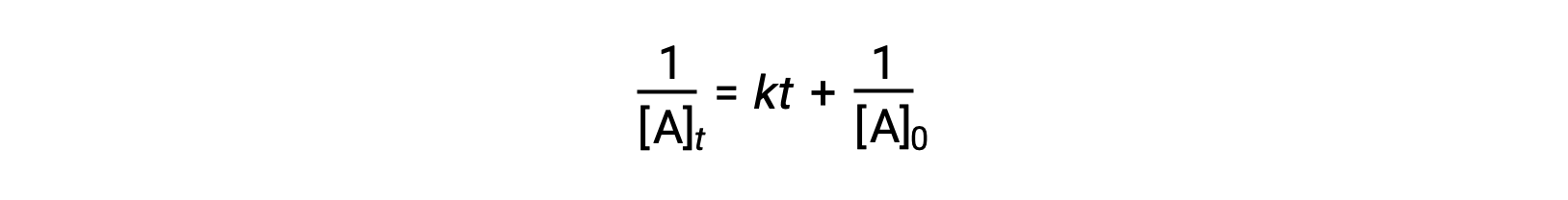
The second-order integrated rate law also takes the form of the equation for a straight line. According to the equation, a plot of 1/[A]_t versus t for a second-order reaction is a straight line with a slope of k and a y-intercept of 1/[A]₀. If the plot is not a straight line, then the reaction is not second-order.

Zero-Order Reactions

For zero-order reactions, the differential rate law is rate = k. A zero-order reaction exhibits a constant reaction rate, regardless of the concentration of its reactant(s). Zero-order kinetics are observed for some reactions only under certain specific conditions. These same reactions exhibit different kinetic behaviors when the specific conditions aren’t met, and for this reason, the more prudent term pseudo-zero-order is sometimes used.

The integrated rate law for a zero-order reaction is also a linear function, taking the form of y = mx + b:

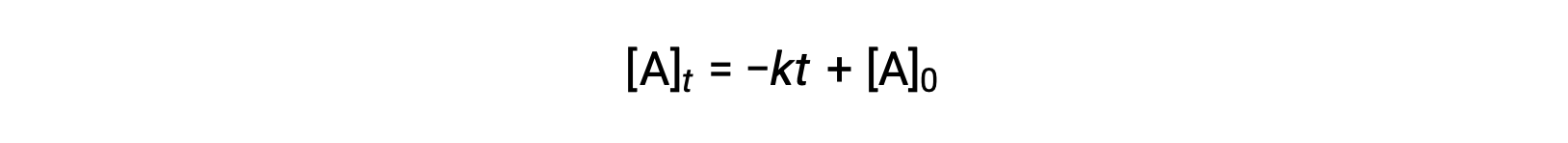
A plot of [A] versus time t for a zero-order reaction is a straight line with a slope of −k and a y-intercept of [A]₀.

This text is adapted from Openstax, Chemistry 2e, Section 12.4: Integrated Rate Laws.