13.7 : Temperature Dependence on Reaction Rate
The Collision Theory
Atoms, molecules, or ions must collide before they can react with each other. Atoms must be close together to form chemical bonds. This premise is the basis for a theory that explains many observations regarding chemical kinetics, including factors affecting reaction rates.
The collision theory is based on the postulates that (i) the reaction rate is proportional to the rate of reactant collisions, (ii) the reacting species collide in an orientation allowing contact between the atoms that become bonded together in the product, and (iii) the collision occurs with adequate energy to permit mutual penetration of the reacting species’ valence shells so that the electrons can rearrange and form new bonds (and new chemical species).
For example, in a gas-phase reaction between carbon monoxide and oxygen, occurring at high temperature and pressure, the first step is a collision between the two molecules.
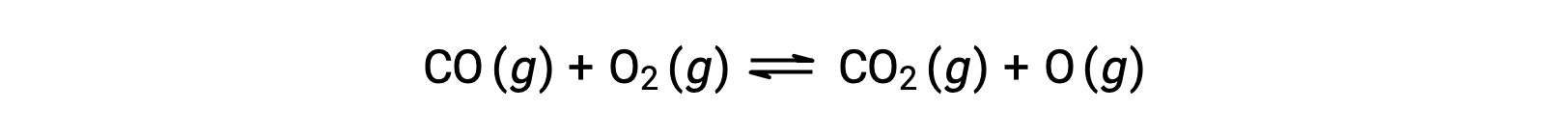
However, there could be many different possible relative orientations in which the two molecules collide. Hence, the orientation of the colliding molecules has great significance in partially determining the feasibility of a reaction occurring between them.
In one instance, the oxygen side of the carbon monoxide molecule may collide with the oxygen molecule. In another instance, the carbon side of the carbon monoxide molecule can collide with the oxygen molecule. The second case is more likely to result in the formation of carbon dioxide, with a central carbon atom bonded to two oxygen atoms (O = C = O).
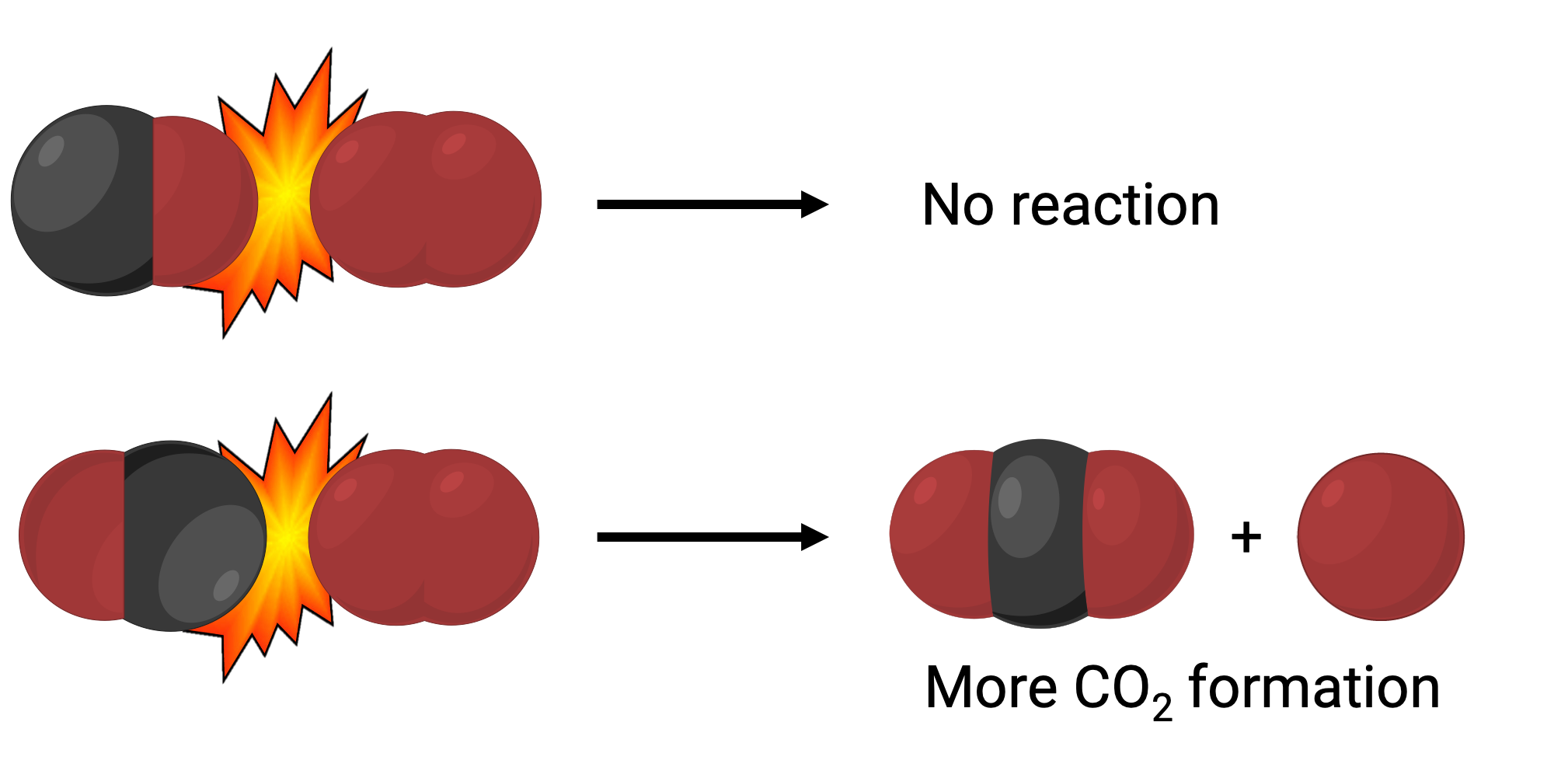
Yet, even if the collision does take place in the correct orientation, the guarantee that the reaction will proceed to form carbon dioxide is limited. This is because, in addition to the proper orientation, the collision must also occur with sufficient energy called activation energy to result in product formation. When reactant species collide with both correct orientation and enough activation energy, they combine to form an unstable species called an activated complex or a transition state. These species are short-lived and usually undetectable by most analytical instruments. In some cases, sophisticated spectral measurements can observe transition states.
Collision theory explains why most reaction rates increase as temperature increases; with an increase in temperature, the frequency of collisions increases. More collisions mean a faster reaction rate, assuming the energy of the collisions is adequate.
Activation Energy
The minimum energy necessary to form a product during a collision between reactants is called the activation energy (Ea). The difference in activation energy required and the kinetic energy provided by colliding reactant molecules is a primary factor affecting the rate of a chemical reaction. If the activation energy is much larger than the average kinetic energy of molecules, the reaction will occur slowly, since only a few fast-moving molecules will have enough energy to react. If the activation energy is much smaller than the molecules' average kinetic energy, a large fraction of molecules will be adequately energetic, and the reaction will proceed rapidly.
Reaction diagrams are widely used in chemical kinetics to illustrate various properties of a reaction of interest. It shows how a chemical system's energy changes as it undergoes a reaction, converting reactants to products.
For instance, consider the following reaction diagram for an exothermic reaction: A + B → C + D;
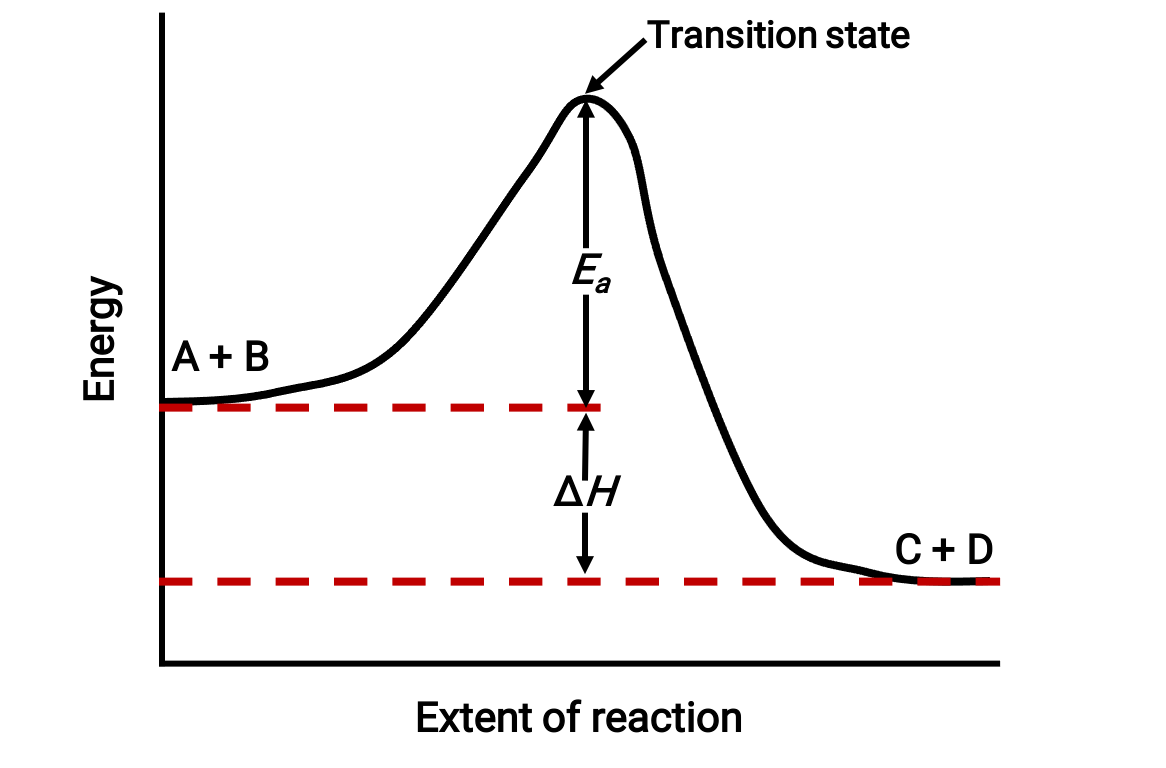
The diagram is viewed from left to right. Initially, the system consists of reactants (A + B) only. Once the reactant molecules with sufficient energy collide, they form a high-energy activated complex or transition state. The unstable transition state then subsequently decays to yield stable products (C + D).
The diagram depicts the reaction's activation energy, Ea, as the energy difference between the reactants and the transition state. The energy difference between the reactants and products corresponds to the enthalpy change of the reaction (ΔH). In this case, the reaction is exothermic (ΔH < 0), since it yields a decrease in the system enthalpy.
Arrhenius Equation
The Arrhenius equation, k = Ae−Ea/RT relates the activation energy and the rate constant, k, for many chemical reactions.
In this equation, R is the ideal gas constant, which has a value 8.314 J/mol·K, T is the temperature in kelvin, Ea is the activation energy in joules per mole, e is the constant 2.7183, and A is a constant called the frequency factor, which is related to the frequency of collisions and the orientation of the reacting molecules. The Arrhenius equation nicely accommodates the postulates of collision theory. The frequency factor, A, reflects how well the reaction conditions favor correctly oriented collisions between reactant molecules. An increased probability of effectively oriented collisions results in larger values for A and faster reaction rates.
The exponential term, e−Ea/RT, describes the effect of activation energy on the reaction rate. According to kinetic molecular theory, the temperature of matter is a measure of the average kinetic energy of its constituent atoms or molecules—a lower activation energy results in a more significant fraction of adequately energized molecules and a faster reaction.
The exponential term also describes the effect of temperature on the reaction rate. A higher temperature represents a correspondingly greater fraction of molecules possessing sufficient energy (RT) to overcome the activation barrier (Ea). This yields a higher value for the rate constant and a correspondingly faster reaction rate.
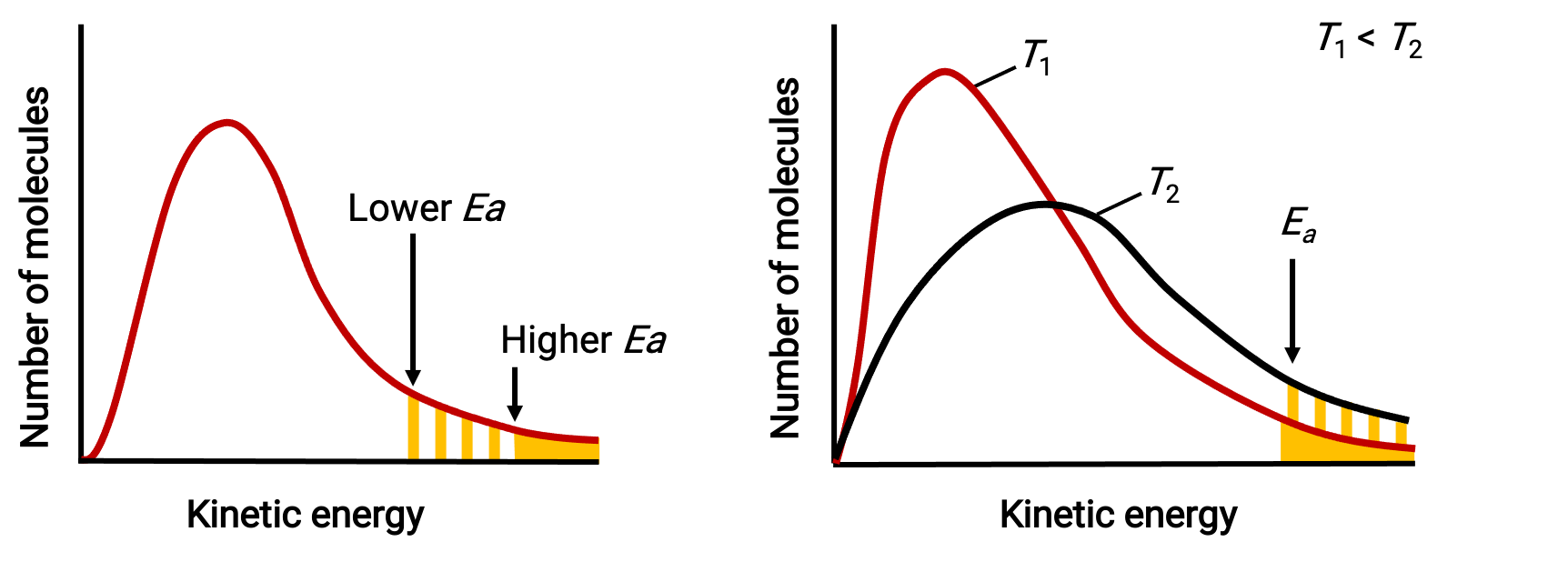
Molecular energy distributions showing numbers of molecules with energies exceeding two different activation energies at a given temperature, and a given activation energy at two different temperatures.
This text is adapted from Openstax, Chemistry 2e, Section 12.5: Collision Theory.
From Chapter 13:

Now Playing
13.7 : Temperature Dependence on Reaction Rate
Chemical Kinetics
77.6K Views

13.1 : Reaction Rate
Chemical Kinetics
43.6K Views

13.2 : Measuring Reaction Rates
Chemical Kinetics
19.7K Views

13.3 : Concentration and Rate Law
Chemical Kinetics
24.9K Views

13.4 : Determining Order of Reaction
Chemical Kinetics
50.3K Views

13.5 : The Integrated Rate Law: The Dependence of Concentration on Time
Chemical Kinetics
28.7K Views

13.6 : Half-life of a Reaction
Chemical Kinetics
31.0K Views

13.8 : Arrhenius Plots
Chemical Kinetics
33.0K Views

13.9 : Reaction Mechanisms
Chemical Kinetics
22.0K Views

13.10 : Rate-Determining Steps
Chemical Kinetics
28.7K Views

13.11 : Catalysis
Chemical Kinetics
24.1K Views

13.12 : Enzymes
Chemical Kinetics
75.9K Views
ABOUT JoVE
Copyright © 2025 MyJoVE Corporation. All rights reserved