Se requiere una suscripción a JoVE para ver este contenido. Inicie sesión o comience su prueba gratuita.
Method Article
Tensor de difusión por resonancia magnética en el análisis de las enfermedades neurodegenerativas
En este artículo
Resumen
Tensor de difusión (DTI), básicamente, sirve como una herramienta basada en RM para identificar In vivo La microestructura del cerebro y los procesos patológicos debido a trastornos neurológicos dentro de la materia blanca cerebral. Análisis DTI basados permiten para su aplicación a las enfermedades del cerebro, tanto a nivel de grupo y en los datos de un solo sujeto.
Resumen
Técnicas de tensor de difusión (DTI) proporcionan información sobre los procesos microestructurales de la sustancia blanca cerebral (WM) in vivo. Las presentes aplicaciones están diseñadas para investigar las diferencias de patrones de participación de WM en diferentes enfermedades cerebrales, trastornos neurodegenerativos, especialmente mediante el uso de diferentes análisis DTI en comparación con los controles emparejados.
Análisis de datos DTI se realiza de forma variable aleatoria, es decir, la comparación de los indicadores regionales voxelwise dirección de difusión basados tales como anisotropía fraccional (FA), junto con el seguimiento de la fibra (FT), acompañado de las estadísticas de anisotropía fraccional tractwise (AGT) de origen a nivel de grupo a fin para identificar diferencias en FA WM a lo largo de las estructuras, con miras a la definición de los patrones regionales de WM alteraciones a nivel de grupo. La transformación en un espacio estándar estereotáxica es un requisito previo para los estudios de grupo y requiere los datos completos del tratamiento para preservar directional interdependencias. Las aplicaciones actuales muestran enfoques técnicos optimizados para esta preservación de la información cuantitativa y direccional durante la normalización espacial en los análisis de datos a nivel de grupo. Sobre esta base, las técnicas de FT se pueden aplicar a los datos promediados de grupo con el fin de cuantificar la información métricas como se define por FT. Además, la aplicación de los métodos de DTI, es decir, diferencias en la AF-mapas después de la alineación estereotáxica, en un análisis longitudinal en función de materias individuales revelan información acerca de la progresión de los trastornos neurológicos. Nuevas mejoras en la calidad de los resultados basados en DTI se puede obtener en la ejecución previa por aplicación de una eliminación controlada de direcciones del gradiente con altos niveles de ruido.
En resumen, DTI se utiliza para definir una clara patoanatomía WM de diferentes enfermedades del cerebro por la combinación de todo DTI análisis basado en el cerebro y el tracto basada.
Introducción
Difusión de imágenes con tensor en el cerebro humano
Los tractos de materia blanca (WM) en el sistema nervioso central consisten en axones densamente empaquetadas, además de diversos tipos de neuroglia y otras pequeñas poblaciones de células. La membrana axonal, así como las fibras de proteína bien alineados dentro de un axón restringe la difusión del agua perpendicular a la orientación de las fibras, dando lugar a la difusión del agua anisotrópico en el cerebro WM 1. Las vainas de mielina alrededor de los axones también pueden contribuir a la anisotropía para tanto intra-y extracelular del agua 2.
La descripción cuantitativa de esta anisotropía se pudo detectar por tensor de difusión (DTI). DTI produce imágenes de los tejidos ponderados con las características microestructurales locales de la difusión del agua. Las intensidades de imagen-en cada posición son atenuadas, en función de la fuerza y la dirección de la llamada gradiente de difusión magnético (representado en-el valor de b), así como en la microestructura local en el que las moléculas de agua se difunden 3, el coeficiente de difusión D, un valor escalar:

Sin embargo, en la presencia de anisotropía en WM, la difusión ya no puede ser caracterizado por un único coeficiente de escalar, pero requiere un tensor  que en primera aproximación describe movilidad molecular a lo largo de cada dirección y la correlación entre estas direcciones 4. Difusión anisotropía es causada principalmente por la orientación de los tractos de fibras en WM y está influenciado por sus micro-y macroestructurales características. De las características microestructurales, organización intraaxonal parece ser de mayor influencia en la anisotropía de difusión, además de la densidad de la fibra unaembalaje de células nd, grado de mielinización, y el diámetro de la fibra individual. En una escala macroscópica, la variabilidad en la orientación de todos los tractos WM en un voxel de imágenes influye en su grado de anisotropía 5.
que en primera aproximación describe movilidad molecular a lo largo de cada dirección y la correlación entre estas direcciones 4. Difusión anisotropía es causada principalmente por la orientación de los tractos de fibras en WM y está influenciado por sus micro-y macroestructurales características. De las características microestructurales, organización intraaxonal parece ser de mayor influencia en la anisotropía de difusión, además de la densidad de la fibra unaembalaje de células nd, grado de mielinización, y el diámetro de la fibra individual. En una escala macroscópica, la variabilidad en la orientación de todos los tractos WM en un voxel de imágenes influye en su grado de anisotropía 5.
En mediciones típicas DTI, los vóxel dimensiones son del orden de milímetros. Por lo tanto, un voxel siempre contiene la información promediada de las moléculas de agua en el interior del volumen detectado que por lo general abarca varios axones, así como las moléculas de agua circundantes. A pesar de este entorno multidireccional, DTI es sensible a la orientación del eje principal más grande que se alinea a la dirección axonal predominante, es decir, la contribución axonal domina la señal medida 2.
DTI ofrece dos tipos de información acerca de la propiedad de la difusión del agua: en primer lugar, la medida independiente de la orientación de la difusión anisotropía 5 y la segunda, la dirección predominante de la difusión del agua en la image vóxeles, es decir, la orientación de difusión 6.
Los protocolos actuales se supone que proporcionan un marco de técnicas de análisis DTI para la comparación cuantitativa de los grupos de asignaturas a nivel de grupo, como se indica a continuación.
La cuantificación de propiedades de difusión - parámetros de análisis
Los elementos del tensor simétrico se pueden medir por gradientes de difusión a lo largo de al menos seis no colineales y no coplanares direcciones, de manera que B (Ecuación 1) se ha convertido en un tensor, lo que resulta en la atenuación de señal
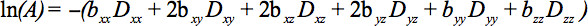
Esta ecuación requiere que representa las posibles interacciones entre imágenes y gradientes de difusión que se aplican en direcciones ortogonales (términos cruzados) e incluso entre los gradientes de formación de imágenes que se aplicanen direcciones ortogonales 4.
El tensor de difusión de segundo orden  siempre se puede diagonalizada dejando sólo tres elementos distintos de cero a lo largo de la diagonal principal del tensor, es decir, los valores propios (
siempre se puede diagonalizada dejando sólo tres elementos distintos de cero a lo largo de la diagonal principal del tensor, es decir, los valores propios ( 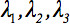 ). Los valores propios reflejan la forma o configuración de la elipsoide. La relación matemática entre las coordenadas principales del elipsoide y el marco de laboratorio es descrito por los vectores propios
). Los valores propios reflejan la forma o configuración de la elipsoide. La relación matemática entre las coordenadas principales del elipsoide y el marco de laboratorio es descrito por los vectores propios 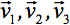
Puesto que hay varios retos en la visualización de datos tensor, el concepto de elipsoides de difusión se ha propuesto 3. Los Eigendiffusivities de estos ellipsoids representan los coeficientes de difusión unidimensionales en la dirección principal de la difusividad del medio, es decir, el eje principal de la elipsoide representa la dirección principal de difusión en el voxel que coincide con la dirección de las fibras, mientras que la excentricidad de la elipsoide proporciona información acerca de la grado de anisotropía y su simetría. Por lo tanto, la difusión de anisotropía métricas tales como la anisotropía fraccional (FA) podrían definirse 7.

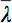 es la media aritmética de todos los valores propios.
es la media aritmética de todos los valores propios.
Un enfoque adicional es el uso de la dirección principal del tensor de difusión para abordar la conectividad WM del cerebro, lo que corresponde a la tractography approach que tiene la intención de investigar qué partes del cerebro están conectadas entre sí. Suponiendo que la orientación del componente principal del tensor de difusión representa la orientación de los tractos axonales dominantes, un campo vectorial 3-D se proporciona en la que cada vector representa la orientación de la fibra. En la actualidad, existen varios enfoques diferentes para reconstruir vías WM que podría dividirse en dos tipos: la primera categoría se basa en algoritmos de propagación de línea utilizando la información tensor local para cada paso de la propagación del tracto de fibra 2,8,9. La segunda categoría se basa en la minimización de la energía global para encontrar la ruta más favorable energéticamente entre dos regiones WM, lo que resulta en el enfoque de las estadísticas espaciales tracto basados en (TBSS) 10 que ha sido utilizado en otros algoritmos, tales como las estadísticas de anisotropía fraccional tractwise (TFAS - véase el texto del protocolo, sección 2.4)..
Transformación en soporte estereotáxicoard espacio
Al igual que en otros métodos avanzados de MRI, DTI-FT y los estudios basados en un contexto clínico persiguen el objetivo final de clasificar la morfología del cerebro de cada paciente con el fin de facilitar el proceso de diagnóstico basada en cierta discriminación métrica 11. Estudios a nivel de grupo son más relevantes si el fenotipo clínico común se supone que es debido a daños en una o más áreas específicas del cerebro o una red neuroanatómicos específicos. Aquí, con un promedio de los resultados para diferentes sujetos es útil con el fin de evaluar los patrones comunes de alteraciones microestructurales. Cada cerebro individual tiene que ser transferido hacia el espacio estereotáxico de manera que, en un segundo paso, el promedio aritmético de los resultados a un nivel de voxel por voxel es posible. Normalización espacial permitió para la aritmética promedio de los resultados obtenidos a partir de diferentes sujetos con el fin de mejorar la relación señal-a-ruido (SNR) y para llevar a cabo una comparación de las muestras de los pacientes y contROLS con el fin de analizar la patoanatomía computacional de un trastorno específico, por ejemplo, una enfermedad neurodegenerativa que se asocia con la afectación de un sistema específico del cerebro.
El enfoque inicial de la normalización a un espacio estereotáxico estandarizada por 12 sugiere un algoritmo de transformación de un atlas estándar que implica la identificación de los distintos hitos del cerebro y poco a poco escala de los cuadrantes del cerebro. Hoy en día, la mayoría de los paquetes de análisis de datos avanzados de resonancia magnética utilizan normalización del Instituto Neurológico de Montreal (MNI) Espacio estereotáxica 13. Para esta transformación, los algoritmos de registro cerebrales semiautomáticas y automáticas con plantillas específicas de estudio se desarrollaron 14,15. En DTI, la atención especial se ha de elaborar para conservar la información de dirección durante el proceso de normalización 16,17. La aplicación de transformaciones espaciales a las imágenes DT-RM de los cuales son necesarios para la normalización espacialde colecciones de conjuntos de datos es, en contraste a las imágenes escalares deformación, complicados por el hecho de que DT contienen información de orientación que está más afectada por la transformación. Este efecto debe tenerse en cuenta con el fin de garantizar la corrección anatómica de la imagen transformada. Aquí, se presentan técnicas para aplicar transformaciones afines a los conjuntos de datos DTI.
Aplicación de DTI a las enfermedades cerebrales
La comparación de DTI longitudinal de datos requiere una alineación / registro de los datos de un objeto entre sí. En ese contexto, es necesaria la conservación de la información direccional (es decir, la rotación del tensor de difusión durante transformaciones afines). Posibles aplicaciones a trastornos neurodegenerativos se ha informado anteriormente (por ejemplo, 18,19).
DTI se ha establecido como una herramienta técnica no invasiva robusta para investigar in vivo Neuropatholgía de WM tractos neuronales (por ejemplo, 11,20,21,22). Métricas cuantitativas DTI basados del proceso de difusión, por ejemplo, el FA, ya han demostrado ser marcadores sensibles para el estudio de una amplia gama de patologías WM, tales como accidente cerebrovascular 20, de la esclerosis múltiple 23, la esclerosis amiotrófica lateral 24, 25, enfermedad de Alzheimer 26 , y varios otros trastornos WM 27,28.
Además, DTI con FT se puede utilizar para identificar extensiones WM 23. Esta técnica, aunque todavía no está en uso clínico de rutina, se está convirtiendo en un poderoso instrumento para la evaluación de anormalidades vía específica en la enfermedad neurológica. Dentro de las zonas identificadas, varios índices MRI cuantitativos derivados de DTI y adquisiciones adicionales (por ejemplo, las imágenes potenciadas en T2 y / o transferencia de magnetización (MT) de imágenes) que son anatómicamente coregistered a los datos DTI puede medir. Por la presente, cada índice puede ser calculATED como una función de la posición dentro del tracto, refiriéndose a las parcelas que representan su variación espacial como perfiles de las vías.
En los siguientes análisis, DTI humanos que se realizaron en 1,5 Tesla MRI-escáneres (Siemens Medical, Erlangen, Alemania) se utilizaron para investigar el potencial de diversas técnicas de análisis para la detección de anomalías de la materia blanca en los grupos de pacientes, así como en individuos. Después de una verificación automática de calidad para la eliminación de los volúmenes de movimiento corruptos y volúmenes con otros tipos de artefactos, procedimientos estandarizados postprocesado preparan los datos DTI para el análisis consecutivo. Diferentes enfoques de análisis se ilustran en la siguiente, es decir, en primer lugar, todo el cerebro con base estadística espacial (WBS), segundo, FT y, estadísticas anisotropía fraccional Tractwise tercero (AGT) de origen. WBSs es un método que se ejecuta en analogía a la morfometría basada en voxel (VBM), que se conoce generalmente como morfometría / estadísticas basada en voxel en DTI datos (VBM / DTI) . VBM es un método que se ejecuta originalmente en las imágenes de contraste donde las diferencias de contraste en exploraciones separadas tienen que ser resueltos mientras WBSs es un método que utiliza la comparación voxelwise de un parámetro físico. Por lo tanto, aunque algorítmicamente similares, una terminología que se está diferenciando WBSs y VBM se utilizará en el siguiente.
Access restricted. Please log in or start a trial to view this content.
Protocolo
Métodos de Análisis: pre y postprocesamiento
La tarea de la siguiente protocolo es analizar propiedades de difusión voxelwise dentro de tractos de sustancia blanca, que podría ser - debido a la detección voxelwise - ya sea isotrópicas o anisotrópicas, lo que resulta en la difusión tensores alargados o achatada para los respectivos elementos de imagen volumétrica. La parametrización de los tensores del voxel se utiliza, ya sea para el cálculo de la FA-mapas o la identificación de fibertracts (Figura 1).
Con el fin de obtener los resultados del análisis como se muestra en la siguiente, utilice el paquete de software de imágenes Tensor y Seguimiento de la fibra (TIFT) 17. TIFT proporciona herramientas de análisis de los siguientes requisitos:
- análisis en términos de DTI métricas, por ejemplo, FA-mapas,
- normalización estereotáxica
- el grupo de comparación en términos de FA u otras métricas DTI
- diversos enfoques de análisis de FT
- FT en grupo promedió DDatos de TI y el análisis estadístico correspondiente.
Estas características permiten una variedad de análisis en un entorno de software 17,29,30,31. El software TIFT está en constante desarrollo de nuevas opciones en el análisis de datos DTI.
La figura 2 ofrece una visión esquemática de cómo analizar los datos DTI a nivel de grupo después de la normalización espacial mediante dos enfoques complementarios, es decir, tanto por WBSs y TFAS para obtener finalmente las diferencias entre las muestras sometidas a nivel de grupo, por ejemplo, los cerebros enfermos frente a controles sanos. Aquí, WBS tiene por objeto la detección imparcial voxelwise de áreas con diferencias a nivel de grupo, mientras que TFAS se basa en fibertracts predefinidos; TFAS las zonas de inicio o bien se puede elegir libremente o se puede derivar de los resultados WBS ('hotspots `de alterado de manera significativa FA).
Comparación longitudinal individual de FA-maps es realizado por detecciónting diferencias en FA-mapas de mediciones en diferentes puntos de tiempo tras la alineación estereotáxica afín (Figura 2).
- Control de calidad (QC), incluyendo la corrección de direcciones gradiente corruptos
En caso de trastornos de movimiento durante la adquisición, es decir, en caso de volúmenes dañados, un aumento SNR se obtiene omitiendo direcciones gradiente individuales (GD) para el cálculo tensorial. Para tal fin, se desarrolló un control de calidad (QC) algoritmo 32. En resumen, en un análisis que contenía volúmenes dañados, un aumento SNR se logra omitiendo direcciones individuales gradiente de uno en uno antes de la estimación tensor de: para cada GD, la varianza ponderada se calcula a partir de todas las direcciones restantes en la secuencia mediante la ponderación con el ángulo en que diferían de el índice de GD.- Realizar una corrección de artefacto mediante la detección de GD con al menos una porción que muestra disminución de la intensidad, es decir, artefactos de movimiento causados por do espontánea movimiento bject (Figura 3, panel superior). Para cualquier volumen ponderado difusión, calcular la intensidad media para cada rebanada y comparar su intensidad con el mismo segmento en todos los demás volúmenes mediante el uso de un enfoque de promedio ponderado - el factor de ponderación es el producto escalar de dos vectores de GD
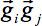 :
: 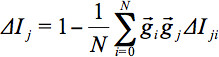
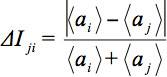
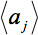 denota la intensidad media aritmética de la rebanada en observación y427eq12.jpg "/> una rebanada de comparación. La desviación promedio de intensidad relativa
denota la intensidad media aritmética de la rebanada en observación y427eq12.jpg "/> una rebanada de comparación. La desviación promedio de intensidad relativa 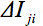 está ponderado por el producto escalar de la GD. Por lo tanto, con el fin de definir un parámetro global:
está ponderado por el producto escalar de la GD. Por lo tanto, con el fin de definir un parámetro global: 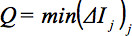
refleja el mínimo de comparaciones slicewise de todas las rebanadas. - Si Q es bajo un cierto umbral (en el ejemplo, un umbral de 0,8 se utiliza para este propósito), eliminar todo ese volumen, o GD. Un umbral de 0,8 se considera una solución estable 32. Figura 3 ilustra los artefactos de movimiento visible en reconstrucciones sagitales y detectada por el algoritmo de control de calidad. En este ejemplo, con respecto al número total de GD (puntos azules en la figura 3c), 17 estaban por debajo de la línea roja que corresponde a Q = 0,8 y Should ser eliminado. Un ejemplo de un volumen de estadísticas de eliminación para un estudio conjunto se presenta en la Figura 3d. En este estudio ejemplar, los datos DTI de 29 sujetos HD presintomáticos se compararon con los datos del DTI de 30 controles. Los detalles adicionales de este algoritmo se presentan en 32, 33.
- Realizar una corrección de artefacto mediante la detección de GD con al menos una porción que muestra disminución de la intensidad, es decir, artefactos de movimiento causados por do espontánea movimiento bject (Figura 3, panel superior). Para cualquier volumen ponderado difusión, calcular la intensidad media para cada rebanada y comparar su intensidad con el mismo segmento en todos los demás volúmenes mediante el uso de un enfoque de promedio ponderado - el factor de ponderación es el producto escalar de dos vectores de GD
- Preprocesamiento y normalización espacial
- Realizar la corrección de las distorsiones geométricas de corriente de Foucault inducidas de los datos de imágenes de eco-planar establece por el método propuesto por 34.
- Para la normalización estereotáxica, crear un estudio específico de (b = 0) - plantilla y un FA-plantilla como se ha descrito anteriormente 17,28,31. Básicamente, una normalización estereotáxica no lineal completo se compone de tres componentes de deformación. En consecuencia, el tensor de difusión resultante
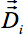 de cada voxel i tiene que ser girandoed de acuerdo a todas las rotaciones mencionadas anteriormente (Figura 4):
de cada voxel i tiene que ser girandoed de acuerdo a todas las rotaciones mencionadas anteriormente (Figura 4): - La figura 4a muestra una transformación rígida cerebro para alinear los marcos de coordenadas básicas. La rotación
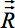 resultante de la alineación para el marco de coordenadas básico tiene que ser aplicada
resultante de la alineación para el marco de coordenadas básico tiene que ser aplicada 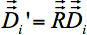
- La figura 4b muestra una deformación lineal de acuerdo con puntos de referencia. Los componentes de los vectores propios
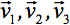 tendrá que ser adaptado de acuerdo con los seis parámetros de normalización de S (depende de la región del cerebro s a,, a = 1 ... 6) de la deformación lineal.
tendrá que ser adaptado de acuerdo con los seis parámetros de normalización de S (depende de la región del cerebro s a,, a = 1 ... 6) de la deformación lineal.
v w, j '' '= S un V W, j'''
w = 1,2,3 y j = x, y, z. - La figura 4c muestra una normalización no lineal igualación de diferencias en la forma del cerebro no lineales. Los desplazamientos vector 3-D son diferentes para cada voxel que conduce a una transformación separada para cada voxel de la matriz del voxel 3-D
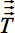 ). Trigonometría estándar da una matriz de rotación de forma independiente para cada voxel, lo que resulta a partir del vector 3-D se desplaza siguiendo los conceptos de 16 con el fin de preservar las relaciones direccionales entre los vectores propios de los voxels neighbored. Por lo tanto, los diferentes turnos de dos voxels neighbored resultan en rotaciones de los vectores propios correspondientes. Usa las matrices de dilatación para la alineación del tensor
). Trigonometría estándar da una matriz de rotación de forma independiente para cada voxel, lo que resulta a partir del vector 3-D se desplaza siguiendo los conceptos de 16 con el fin de preservar las relaciones direccionales entre los vectores propios de los voxels neighbored. Por lo tanto, los diferentes turnos de dos voxels neighbored resultan en rotaciones de los vectores propios correspondientes. Usa las matrices de dilatación para la alineación del tensor 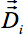 de cada voxel alos voxels adyacentes.
de cada voxel alos voxels adyacentes. 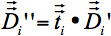
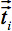 son los componentes de
son los componentes de 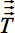
- La figura 4a muestra una transformación rígida cerebro para alinear los marcos de coordenadas básicas. La rotación
- Después de este procedimiento de normalización individual (step (i) - DTI-data I 0), utilice todos los datos individuales DTI establece para la creación de un estudio específico (b = 0) - plantilla y una plantilla de FA (etapa (ii) - Plantillas T 1). A medida que el registro no afín a un FA-plantilla tiene la ventaja de que proporciona un mayor contraste en comparación con (b = 0) imágenes 10, definen un FA-plantilla el promedio de todas derivado individualmente FA-mapas de los pacientes y los controles.
- En un segundo paso, después de las ideas básicas de Ashburner y Friston 35, lleve a cabo una normalización MNI no lineal (la etapa (iii)) de los datos DTI establece al minimizar la falta de correspondencia entre las intensidades regionales de la FA-mapa para montar y de el FA-plantilla de acuerdo con las diferencias al cuadrado (X 2) - de esa manera, obtener datos DTI I 1.
- Basándose en estos datos, nuevas plantillas T 2 se derivan (etapa (iv)). Repita este proceso iterativo hasta que la correlación entre el individuo FA-mapas y tél FA-plantilla es> 0,7. Por lo general, esto se alcanza después de dos iteraciones.
- Whole estadísticas espaciales basadas en el cerebro
Los siguientes pasos 1.3.1 hasta 1.3.5 se representan de forma esquemática en la Figura 5b.- Calcular FA-mapas a partir de datos DTI normalizadas con respecto al procedimiento de normalización de 1,2. con el fin de preservar la información direccional (etapa (i)).
- Como un paso de preprocesamiento antes de la comparación estadística voxelwise, aplicar un filtro de suavizado (etapa (ii)) a la normalizada FA-mapas individuales. Para el acondicionamiento, el hecho de que el tamaño del filtro influye en los resultados de análisis de datos DTI 36 requiere la aplicación del teorema de filtro adaptado que se afirma que la anchura del filtro utilizado para procesar los datos se debe adaptar al tamaño de la diferencia esperada, como se detalla en aplicaciones anteriores a los datos DTI de pacientes con trastornos neurodegenerativos (por ejemplo, 28).
- Realizar estadística borradorarison entre los grupos de pacientes y el correspondiente grupo voxelwise control por parte de la t de Student prueba, es decir, comparar los valores de FA de los pacientes con AF-mapas con los valores de FA de los controles 'FA-mapas, para cada voxel separadamente (etapa (iii )). No se consideran los valores de FA por debajo de 0,2 para el cálculo ya que la materia gris cortical muestra los valores de FA hasta 0,2 37.
- Los resultados estadísticos tienen que ser corregido para comparaciones múltiples utilizando el falso descubrimiento tasa (FDR) algoritmo de p <0.05 38 (etapa (iv)). Una mayor reducción del error alfa tiene que ser realizado por un algoritmo de correlación espacial (la agrupación - la etapa (v)) que elimina los voxels aisladas o en pequeños grupos aislados de elementos de imagen volumétrica en el rango de tamaño del kernel de suavizado, que conduce a un tamaño de clúster umbral de 512 voxels.
- Para mostrar los resultados en un fondo morfológica (etapa (v)), normalizar los 3 D-T1 datos ponderados establece a MNI espacio y media aritmética. Lleve a cabo esta normalización procedimiento mediante el uso de una plantilla específica del estudio en analogía a la normalización aplicada a los datos DTI fija 17.
La Figura 6 muestra los resultados de los enteros estadísticas espaciales basadas en el cerebro (WBS) de los pacientes de ALS frente a los controles. Figura 6a muestra el máximo local de la disminución de los valores de FA en un sagital, coronar y vista axial (thresholded en p <0,01, corregidos para múltiples comparaciones). Figura 6B muestra FT proyectual con puntos de partida en el tracto corticoespinal utilizado como base para TFAS. Figura 6c muestra diferencias de grupo en FA-mapas detectados por todo el cerebro con base estadística espacial (WBS) entre una muestra de pacientes con ELA y controles emparejados en una visualización slicewise.
- Tractografía y estadísticas anisotropía fraccional tractwise (AGT) de origen
La Figura 7 ilustra el proceso de FT grupo basado incluyendo TFAS como se describe en 1.4.1 hasta 1.4.4.- Para la aplicación de algoritmos basados en el grupo M, generará un promedio de DTI conjuntos de datos de "datos y de los controles de los pacientes los datos en conjunto de acuerdo a los métodos descritos anteriormente 17. Este promedio requiere un tratamiento cuidadoso de la información de orientación que se conserva durante el proceso de normalización de acuerdo con las técnicas descritas por 16 - para más detalles, véase 30.
- Realizar tractography en los conjuntos de datos DTI promedio de los grupos de asignaturas mediante la aplicación de una técnica de agilizar el seguimiento 31. Identificar los puntos de semillas definidas manualmente adyacentes a los máximos locales por todo el análisis FA basadas en el cerebro que son la base para el análisis FT consecutivo. Después de la identificación de las semillas, realizar tractography y definir los elementos de imagen volumétrica de las fibras delineadas como una máscara específico de grupo para la siguiente TFAS 30.
- Con el fin de cuantificar los resultados tractografía, aplicar la técnica de ácidos grasos trans con thtractos de fibras e que se crearon en los datos DTI promedio conjuntos de todos los sujetos de cada grupo (los datos del paciente y los datos de control en conjunto) para la selección de los voxels que contribuyen a una comparación entre los pacientes y los controles 'FA-mapas.
- Considere todos los voxels resultantes con un valor de FA por encima de 0,2 para el análisis estadístico de la t de Student prueba.
- Si se desea, la técnica de TFAS se podría aplicar a las mediciones del DTI derivados, tales como la difusividad media (MD), anisotropía de anisotropía axial, radial, etc (por ejemplo, véase 28).
- Los resultados se muestran en un fondo morfológico consiste en las MNI-normalizadas 3 D-series potenciadas en T1 de datos
Access restricted. Please log in or start a trial to view this content.
Resultados
1. Control de calidad y la corrección en direcciones gradiente dañados en aplicación a los datos de los pacientes con trastornos hipercinéticos
Como un ejemplo para el efecto de la aplicación de control de calidad y de exclusión de volumen posterior (como consecuencia de la corrección para los corruptos de GD), la Figura 8 muestra las diferencias en enteros estadísticas espaciales basados en cerebro con y sin exclusión de volumen para la comparación grupo de 29 ...
Access restricted. Please log in or start a trial to view this content.
Discusión
Inter-sujetos promedio de DTI de datos se puede lograr con respecto a la amplitud de difusión (mediante el uso de la información FA) y la dirección de difusión (en base a FT), respectivamente. Promedio de los mapas FA permite la comparación estadística de los grupos de asignaturas por WBSs y TFAS. Este marco metodológico ofrece una introducción a las técnicas de DTI con un promedio entre los sujetos y el grupo de comparación. Normalización estereotáxica y la comparación de los mapas de la FA a nivel de grup...
Access restricted. Please log in or start a trial to view this content.
Divulgaciones
Los autores tienen nada que revelar.
Agradecimientos
Partes de este trabajo, es decir, el estudio de control de calidad y la corrección en direcciones gradiente dañados en aplicación a los datos de los pacientes con trastornos hipercinéticos, recibieron el apoyo de la red europea de alta definición (proyecto EHDN 070). Las imágenes por resonancia magnética en el estudio determinado se adquirieron como parte del sitio cohorte TRACK-HD de Londres.
Access restricted. Please log in or start a trial to view this content.
Materiales
| Name | Company | Catalog Number | Comments |
| MR scanner | Siemens 1.5 T Magnetom Symphony | ||
| analysis software | TIFT - Tensor Imaging and Fiber Tracking |
Referencias
- Moseley, M. E., Cohen, Y., et al. Diffusion-weighted MR imaging of anisotropic water diffusion in cat central nervous system. Radiology. 176, 439-445 (1990).
- Mori, S., van Zijl, P. C. M. Fiber tracking: principles and strategies - a technical review. NMR Biomed. 15, 468-480 (2002).
- Basser, P. J., Mattiello, J., LeBihan, D. MR Diffusion Tensor Spectroscopy and Imaging. Biophys J. 66, 259-267 (1994).
- Mattiello, J., Basser, J. P., Le Bihan, D. Analytical expression for the b-matrix in NMR diffusion imaging and spectroscopy. J. Magn. Reson. A. 108, 131-141 (1994).
- Pierpaoli, C., Basser, P. J. Toward a quantitative assessment of diffusion anisotropy. Magn. Reson. Med. 36, 893-906 (1996).
- Pajevic, S., Pierpaoli, C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: application to white matter fiber tract mapping in the human brain. Magn. Reson. Med. 42, 526-540 (1999).
- Le Bihan, D., Mangin, J. F., et al. Diffusion tensor imaging: concepts and applications. J. Magn. Reson. Imaging. 13, 534-546 (2001).
- Conturo, T. E., Lori, N. F., et al. Tracking neuronal fibre pathways in the living human brain. Proc. Natl. Acad. Sci. U.S.A. 96, 10422-10427 (1999).
- Lori, N. F., Akbudak, E. Diffusion tensor fibre tracking of human brain connectivity: aquisition methods, reliability analysis and biological results. NMR Biomed. 15, 494-515 (2002).
- Smith, S. M., Jenkinson, M., et al. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 31, 1487-1505 (2006).
- Agosta, F., Pagani, E., et al. Assessment of white matter tract damage in patients with amyotrophic lateral sclerosis: a diffusion tensor MR imaging tractography study. AJNR. Am. J. Neuroradiol. 31, 1457-1461 (2010).
- Talairach, J., Tournoux, P. Coplanar stereotaxic atlas of the human brain. , Thieme Medical. New York. (1988).
- Brett, M., Johnsrude, I. S., Owen, A. M. The problem of functional localization in the human brain. Nat. Rev. Neurosci. 3, 243-249 (2002).
- Collins, D. L., Neelin, P., Peters, T. M., Evans, A. C. Automatic 3-D intersubject registration of MR volumetric data in standardized Talairach space. J. Comput. Assist. Tomogr. 18, 192-205 (1994).
- Friston, K. J., Ashburner, J., Frith, C. D., Poline, J. -B., Heather, J. D., Frackowiak, R. S. J. Spatial registration and normalization of images. Human Brain Mapp. 2, 165-189 (1995).
- Alexander, D. C., Pierpaoli, C., Basser, P. J., Gee, J. C. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans. Med. Imaging. 20, 1131-1139 (2001).
- Müller, H. -P., Unrath, A., Ludolph, A. C., Kassubek, J. Preservation of Diffusion Tensor Properties during Spatial Normalization by use of Tensor imaging and Fiber Tracking on a Normal Brain Database. Phys. Med. Biol. 52, N99-N109 (2007).
- Likitjaroen, Y., Meindl, T., et al. Longitudinal changes of fractional anisotropy in Alzheimer's disease patients treated with galantamine: a 12-month randomized, placebo-controlled, double-blinded study. Eur. Arch. Psychiatry Clin. Neurosci. 262, 341-350 (2012).
- Zhang, Y., Schuff, N. Progression of white matter degeneration in amyotrophic lateral sclerosis: A diffusion tensor imaging study. Amyotroph. Lateral Scler. 12, 421-429 (2011).
- Pierpaoli, C., Barnett, A. Water diffusion changes in Wallerian degeneration and their dependence on white matter architecture. Neuroimage. 13, 1174-1185 (2001).
- Agosta, F., Valsasina, P., et al. Sensorimotor functional connectivity changes in amyotrophic lateral sclerosis. Cereb Cortex. 21, 2291-2298 (2011).
- Müller, H. -P., Unrath, A., Huppertz, H. J., Ludolph, A. C., Kassubek, J. Neuroanatomical patterns of cerebral white matter involvement in different motor neuron diseases as studied by diffusion tensor imaging analysis. Amyotroph Lateral Scler. 13, 254-264 (2012).
- Reich, D. S., Zackowski, K. M. Corticospinal tract abnormalities are associated with weakness in multiple sclerosis. Am. J. Neuroradiol. 29, 333-339 (2008).
- Abe, O., Yamada, H. Amyotrophic lateral sclerosis: Diffusion tensor tractography and voxel-based analysis. NMR Biomed. 17, 411-416 (2004).
- Sage, C. A., Peeters, R. R., Gorner, A., Robberecht, W., Sunaert, S. Quantitative diffusion tensor imaging in amyotrophic lateral sclerosis. Neuroimage. 34, 486-499 (2007).
- Preti, M. G., Baglio, F., et al. Assessing corpus callosum changes in Alzheimer's disease: comparison between tract-based spatial statistics and atlas-based tractography. PLoS One. 7, e35856(2012).
- Borroni, B., Brambati, S. M., et al. Evidence of white matter changes on diffusion tensor imaging in frontotemporal dementia. Arch. Neurol. 64, 246-251 (2007).
- Unrath, A., Müller, H. -P., Riecker, A., Ludolph, A. C., Sperfeld, A. D., Kassubek, J. Whole brain-based analysis of regional white matter tract alterations in rare motor neuron diseases by diffusion tensor imaging. Hum Brain Mapp. 31, 1727-1740 (2010).
- Müller, H. -P., Lulé, D., Unrath, A., Ludolph, A. C., Riecker, A., Kassubek, J. Complementary Image Analysis of Diffusion Tensor Imaging and 3-Dimensional T1-Weighted Imaging: White Matter Analysis in Amyotrophic Lateral Sclerosis. J. Neuroimaging. 21, 24-33 (2011).
- Müller, H. -P., Unrath, A., Sperfeld, A. D., Ludolph, A. C., Riecker, A., Kassubek, J. Diffusion tensor imaging and tractwise fractional anisotropy statistics: quantitative analysis in white matter pathology. Biomed. Eng. Online. 6, 42(2007).
- Müller, H. -P., Unrath, A., Riecker, A., Pinkhardt, E. H., Ludolph, A. C., Kassubek, J. Inter-subject variability in the analysis of diffusion tensor imaging at the group level: fractional anisotropy mapping and fiber tracking techniques. Magn. Reson. Imaging. 27, 324-334 (2009).
- Müller, H. -P., Glauche, V., et al. Stability of white matter changes related to Huntington's disease in the presence of imaging noise: a DTI study. PLoS Curr. 3, RRN1232(2011).
- Müller, H. -P., Süßmuth, S. D., Landwehrmeyer, G. B., Ludolph, A. C., Tabrizi, S. J., Klöppel, S., Kassubek, J. Stability effects on results of diffusion tensor imaging analysis by reduction of the number of gradient directions due to motion artifacts: an application to presymptomatic Huntington's disease. PLoS Curr. 3, RRN1292(2011).
- Shen, Y., Larkman, D. J., Counsell, S., Pu, I. M., Edwards, D., Hajnal, J. V. Correction of High-Order Eddy Current Induced Geometric Distortion in Diffusion-Weighted Echo-Planar images. Magn. Reson. Med. 52, 1184-1189 (2004).
- Ashburner, J., Friston, K. J. Nonlinear Spatial Normalization Using Basis Functions. Human Brain Mapping. 7, 254-266 (1999).
- Jones, D. K., Symms, M. R., Cercignani, M., Howard, R. J. The effect of filter size on VBM analyses of DT-MRI data. Neuroimage. 26, 546-554 (2005).
- Kunimatsu, A., Aoki, S., et al. The optimal trackability threshold of fractional anisotropy for diffusion tensor tractography of the corticospinal tract. Magn. Reson. Med. Sci. 3, 11-17 (2004).
- Genovese, C. R., Lazar, N. A., Nichols, T. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage. 15, 870-878 (2002).
- Cleaver, J. E. Defective repair replication of DNA in xeroderma pigmentosum. Nature. 218, 652-656 (1968).
- Anttinen, A., Koulu, L., et al. Neurological symptoms and natural course of xeroderma pigmentosum. Brain. 131, 1979-1989 (2008).
- Kassubek, J., Sperfeld, A. D. The cerebro-morphological fingerprint of a progeroid syndrome: white matter changes correlate with neurological symptoms in xeroderma pigmentosum. PLoS One. 7, e30926(2012).
- Canu, E., Agosta, F. The topography of brain microstructural damage in amyotrophic lateral sclerosis assessed using diffusion tensor MR imaging. AJNR. Am. J. Neuroradiol. 32, 1307-1314 (2011).
- Verstraete, E., Veldink, J. H., Hendrikse, J., Schelhaas, H. J., van den Heuvel, M. P., van den Berg, L. H. Structural MRI reveals cortical thinning in amyotrophic lateral sclerosis. J. Neurol. Neurosurg. Psychiatry. 83, 383-388 (2012).
- Hofer, S., Frahm, J. Topography of the human corpus callosum revisited- comprehensive fiber tractography using diffusion tensor magnetic resonance imaging. Neuroimage. 32, 989-994 (2006).
- Iwata, N. K., Kwan, J. Y., et al. White matter alterations differ in primary lateral sclerosis and amyotrophic lateral sclerosis. Brain. 134, 2642-2655 (2011).
- Kassubek, J., Ludolph, A. C., Müller, H. -P. Neuroimaging of motor neuron diseases. Ther. Adv. Neurol. Disord. 5, 119-127 (2012).
- Kassubek, J., Juengling, F. D. Multimodality functional neuroimaging. In: C. Stippich (Ed.): Clinical functional MRI - Presurgical functional neuroimaging. , Springer. Berlin/Heidelberg/New York. (2007).
- Stadlbauer, A., Buchfelder, M., Salomonowitz, E., Ganslandt, O. Fiber density mapping of gliomas: histopathologic evaluation of a diffusion-tensor imaging data processing method. Radiology. , 257-846 (2010).
- Stadlbauer, A., Hammen, T., et al. Differences in metabolism of fiber tract alterations in gliomas: a combined fiber density mapping and magnetic resonance spectroscopic imaging study. Neurosurgery. 71, 454-463 (2012).
- Staempfli, P., Jaermann, T., Crelier, G. R., Kollias, S., Valavanis, A., Boesiger, P. Resolving fiber crossing using advanced fast marching tractography based on diffusion tensor imaging. Neuroimage. 30, 110-120 (2006).
- Ehricke, H. H., Otto, K. M., Klose, U. Regularization of bending and crossing white matter fibers in MRI Q-ball fields Magn. Reson Imaging. 29, 916-926 (2011).
- Hirsch, J. G., Schwenk, S. M., Rossmanith, C., Hennerici, M. G., Gass, A. Deviations from the diffusion tensor model as revealed by contour plot visualization using high angular resolution diffusion-weighted imaging (HARDI). MAGMA. 16, 93-102 (2003).
- Lazar, M., Weinstein, D. M., et al. White matter tractography using diffusion tensor deflection. Human Brain Mapping. 18, 306-321 (2003).
- Reisert, M., Mader, I., Anastasopoulos, C., Weigel, M., Schnell, S., Kiselev, V. Global fiber reconstruction becomes practical. Neuroimage. 54, 955-962 (2011).
- Klein, A., Andersson, J. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage. 46, 786-802 (2009).
- Bammer, R. Basic principles of diffusion-weighted imaging. Eur. J. Radiol. 45, 169-184 (2003).
- Mohammadi, S., Keller, S. S. The influence of spatial registration on detection of cerebral asymmetries using voxel-based statistics of fractional anisotropy images and TBSS. PLoS One. 7, e36851(2012).
- Turner, M. R., Grosskreutz,, et al. Towards a neuroimaging biomarker for amyotrophic lateral sclerosis. Lancet Neurol. 10, 400-403 (2011).
- Müller, H. -P., Kassubek, J. Multimodal imaging in neurology - special focus on MRI applications and MEG. Synthesis Lectures in Biomedical Engineering. Enderle, J. D. 16, Morgan & Claypool Publishers. (2008).
- Douaud, G., Filippini, N., Knight, S., Talbot, K., Turner, M. R. Integration of structural and functional magnetic resonance imaging in amyotrophic lateral sclerosis. Brain. 134, 3470-3479 (2011).
- Kolind, S. H., Laule, C., et al. Complementary information from multi-exponential T2 relaxation and diffusion tensor imaging reveals differences between multiple sclerosis lesions. Neuroimage. 40, 77-85 (2008).
- Verma, R., Zacharaki, E. I. Multiparametric tissue characterization of brain neoplasms and their recurrence using pattern classification of MR images. Acad. Radiol. 15, 966-977 (2008).
Access restricted. Please log in or start a trial to view this content.
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoExplorar más artículos
This article has been published
Video Coming Soon
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados