È necessario avere un abbonamento a JoVE per visualizzare questo. Accedi o inizia la tua prova gratuita.
Method Article
Diffusion Tensor Imaging a risonanza magnetica in Analisi delle Malattie Neurodegenerative
In questo articolo
Riepilogo
Tensore di diffusione (DTI) serve essenzialmente come strumento di risonanza magnetica-based per identificare In vivo La microstruttura del cervello e processi patologici a causa di disturbi neurologici all'interno della sostanza bianca cerebrale. Analisi DTI-based consentono l'applicazione a malattie del cervello, sia a livello di gruppo e di dati di singoli soggetti.
Abstract
Tensore della diffusione tecniche (DTI) forniscono informazioni sui processi microstrutturali della sostanza bianca cerebrale (WM) in vivo. Le attuali applicazioni sono progettate per indagare le differenze di modelli WM coinvolgimento in diverse malattie cerebrali, disturbi neurodegenerativi, in particolare mediante l'uso di differenti analisi DTI a confronto con controlli appaiati.
L'analisi dei dati DTI viene eseguita in maniera variata, ossia il confronto voxelwise di metriche regionali di diffusione direzione-based come anisotropia frazionaria (FA), insieme con il monitoraggio in fibra (FT) accompagnato da statistiche anisotropia frazionaria tractwise (TFAS) a livello di gruppo al fine per individuare differenze nelle FA lungo strutture WM, finalizzate alla definizione di modelli regionali di WM alterazioni a livello di gruppo. Trasformazione in uno spazio standard di stereotassico è un prerequisito per gli studi di gruppo e richiede dati accurati elaborazione di preservare directional interdipendenze. Le attuali applicazioni mostrano approcci tecnici ottimizzati per questa conservazione delle informazioni quantitative e direzionali durante la normalizzazione spaziale in analisi dei dati a livello di gruppo. Su questa base, FT tecniche possono essere applicate al gruppo dati mediati per quantificare informazioni metriche come definito da FT. Inoltre, l'applicazione di metodi di DTI, cioè differenze nelle mappe FA-dopo allineamento stereotassico, in un'analisi longitudinali a base individuale soggette rivelare informazioni sulla progressione dei disturbi neurologici. Ulteriore miglioramento della qualità dei risultati basati DTI può essere ottenuto durante il pre-elaborazione per l'applicazione di una eliminazione controllata delle direzioni gradiente con alti livelli di rumore.
In sintesi, DTI viene utilizzato per definire una distinta WM pathoanatomy di malattie cerebrali diverse dalla combinazione di DTI intera analisi basata sul cervello e del tratto-based.
Introduzione
Tensore della diffusione nel cervello umano
Materia (WM) tratti bianchi nel sistema nervoso centrale consistono di assoni densamente oltre a vari tipi di neuroglia e altre piccole popolazioni di cellule. La membrana assonale nonché le fibre proteiche ben allineati entro un assone limita acqua diffusione perpendicolare all'orientamento fibra, portando a diffusione dell'acqua anisotropo cervello WM 1. Guaine di mielina intorno agli assoni possono anche contribuire alla anisotropia sia per l'acqua intra ed extracellulare 2.
La descrizione quantitativa di questa anisotropia potrebbe essere rilevato dal tensore di diffusione (DTI). DTI produce immagini dei tessuti ponderata con le caratteristiche microstrutturali locali di diffusione dell'acqua. Le immagini-intensità in ogni posizione sono attenuate, a seconda della forza e la direzione del cosiddetto gradiente di diffusione magnetico (rappresentato inil valore-b), nonché dalla microstruttura locale nel quale le molecole di acqua diffondono 3, il coefficiente di diffusione D, un valore scalare:

Tuttavia, in presenza di anisotropia in WM, diffusione può più essere caratterizzato da un unico coefficiente scalare, ma richiede un tensore  che in prima approssimazione descrive la mobilità molecolare lungo ogni direzione e la correlazione tra queste direzioni 4. Diffusione anisotropia è causata principalmente da l'orientamento dei tratti di fibre in WM ed è influenzato dalle sue caratteristiche micro e macrostrutturale. Delle caratteristiche microstrutturali, organizzazione intraaxonal appare di massima influenza sulla diffusione anisotropia, oltre alla densità delle fibre alimballaggio cella nd, grado di mielinizzazione, e diametro delle fibre individuale. Su scala macroscopica, la variabilità nella orientamento di tutte le vie WM in un voxel di imaging influenza il grado di anisotropia 5.
che in prima approssimazione descrive la mobilità molecolare lungo ogni direzione e la correlazione tra queste direzioni 4. Diffusione anisotropia è causata principalmente da l'orientamento dei tratti di fibre in WM ed è influenzato dalle sue caratteristiche micro e macrostrutturale. Delle caratteristiche microstrutturali, organizzazione intraaxonal appare di massima influenza sulla diffusione anisotropia, oltre alla densità delle fibre alimballaggio cella nd, grado di mielinizzazione, e diametro delle fibre individuale. Su scala macroscopica, la variabilità nella orientamento di tutte le vie WM in un voxel di imaging influenza il grado di anisotropia 5.
In tipiche misure DTI, le dimensioni voxel sono dell'ordine dei millimetri. Così, un voxel contiene sempre le informazioni mediata delle molecole d'acqua all'interno del volume rilevato che copre solitamente parecchi assoni e le molecole d'acqua circostanti. Nonostante questo ambiente multidirezionale, DTI è sensibile all'orientamento del più grande asse principale che allinea alla direzione assonale predominante, cioè il contributo assonale domina il segnale misurato 2.
DTI fornisce due tipi di informazioni sulla proprietà di diffusione dell'acqua: la prima, nella misura orientamento indipendente di diffusione anisotropia 5 e la seconda, la direzione predominante di diffusione dell'acqua in imagelettroniche voxel, cioè l'orientamento diffusione 6.
Gli attuali protocolli sono tenuti a fornire un quadro di tecniche di analisi DTI per la comparazione quantitativa dei gruppi di soggetti a livello di gruppo, come indicato di seguito.
Quantificazione di proprietà di diffusione - parametri di analisi
Gli elementi del tensore simmetrico possono essere misurati con gradienti di diffusione lungo almeno sei non collineari e non coplanari direzioni modo che b (Equazione 1) è diventato un tensore, con conseguente attenuazione del segnale
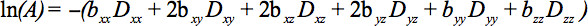
Questa equazione richiede la contabilità per le possibili interazioni tra imaging e gradienti di diffusione che vengono applicate in direzioni ortogonali (termini trasversali) e anche tra i gradienti di imaging che vengono applicatein quattro direzioni ortogonali.
Il tensore di diffusione di secondo rango  può sempre essere diagonalizzata lasciando solo tre elementi diversi da zero lungo la diagonale principale del tensore, cioè gli autovalori (
può sempre essere diagonalizzata lasciando solo tre elementi diversi da zero lungo la diagonale principale del tensore, cioè gli autovalori ( 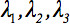 ). Gli autovalori riflettono la forma o configurazione dell'ellissoide. La relazione matematica fra le coordinate principale dell'ellissoide e il telaio laboratorio è descritto da autovettori
). Gli autovalori riflettono la forma o configurazione dell'ellissoide. La relazione matematica fra le coordinate principale dell'ellissoide e il telaio laboratorio è descritto da autovettori 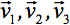
Poiché ci sono diverse sfide nella visualizzazione dati tensoriali, il concetto di ellissoidi di diffusione è stato proposto 3. Le Eigendiffusivities di queste ellipsoids rappresentano i coefficienti di diffusione unidimensionali nella direzione principale della diffusività del mezzo, cioè l'asse principale dell'ellissoide rappresenta la direzione principale di diffusione nel voxel che coincide con la direzione delle fibre, mentre l'eccentricità dell'ellissoide fornisce informazioni sul grado di anisotropia e la sua simmetria. Pertanto, diffusione metriche anisotropia come l'anisotropia frazionaria (FA) potrebbero essere definiti 7.

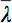 è la media aritmetica di tutti gli autovalori.
è la media aritmetica di tutti gli autovalori.
Un ulteriore approccio è quello di utilizzare la direzione principale del tensore di diffusione per affrontare la connettività WM del cervello, corrispondenti ai trattografia avvicinamench che ha l'intenzione di indagare quali parti del cervello sono collegati tra loro. Supponendo che l'orientamento del componente principale del tensore di diffusione rappresenta l'orientamento dei tratti assonali dominanti, un campo vettoriale 3-D viene fornito in cui ogni vettore rappresenta l'orientamento delle fibre. Attualmente, ci sono diversi approcci per ricostruire WM tratti che possono essere suddivisi in due tipi: la prima categoria si basa sulla linea di algoritmi di propagazione utilizzando le informazioni tensore locale per ogni fase del tratto di propagazione in fibra di 2,8,9. La seconda categoria si basa sulla minimizzazione globale di energia per trovare il percorso energeticamente più favorevole tra le due regioni WM, con conseguente approccio di statistica spaziale tratto basati (TBSS) 10, che è stato utilizzato in altri algoritmi, come le statistiche di anisotropia frazionaria tractwise (TFAS - vedi testo del protocollo, sezione 2.4)..
Trasformazione in supporto stereotassicaard spazio
Come in altri metodi MRI avanzati, e DTI-FT studi basati in un contesto clinico perseguono l'obiettivo finale di categorizzare morfologia cerebrale del singolo paziente, al fine di facilitare il processo diagnostico basato su qualche discriminazione metrica 11. Studi a livello di gruppo sono più pertinenti se il fenotipo clinico comune dovrebbe essere causa di danni a una o più aree specifiche del cervello o una specifica rete neuroanatomici. Qui, con una media dei risultati per diversi soggetti è utile per valutare i modelli comuni di alterazioni microstrutturali. Ogni cervello individuale deve essere trasferito nello spazio stereotassico modo che, in una seconda fase, la media aritmetica dei risultati a un livello voxel per voxel è possibile. Normalizzazione spaziale consentito per media aritmetica dei risultati ottenuti da soggetti diversi al fine di migliorare il rapporto segnale-rumore (SNR) e per eseguire un confronto di campioni di pazienti e controls per analizzare la pathoanatomy computazionale di un disturbo specifico, ad esempio una malattia neurodegenerativa che è associato con l'affettazione di un sistema cerebrale specifico.
L'approccio iniziale di normalizzazione di uno spazio stereotassico standard da 12 ha suggerito un algoritmo di trasformazione di un atlante di serie che coinvolge l'identificazione dei vari punti di riferimento del cervello e frammentario di scala di quadranti del cervello. Al giorno d'oggi, la maggior parte dei pacchetti di analisi dei dati di risonanza magnetica avanzate usano la normalizzazione del Montreal Neurological Institute (MNI) spazio stereotassico 13. Per questa trasformazione, algoritmi registrazione del cervello semiautomatici e automatici utilizzando i modelli specifici di studio sono stati sviluppati 14,15. In DTI, particolare attenzione deve essere redatto per preservare le informazioni direzionali durante il processo di normalizzazione 16,17. L'applicazione di trasformazioni spaziali per immagini DT-MR che sono richiesti per normalizzazione spazialedi collezioni di insiemi di dati sono, rispetto alle immagini scalari orditura, complicata dal fatto che DTs contengono informazioni orientazionale che è di nuovo influenzato dalla trasformazione. Questo effetto deve essere contabilizzato per garantire la correttezza anatomica dell'immagine trasformata. Qui, le tecniche per l'applicazione di trasformazioni affini ai set di dati DTI sono presentati.
Applicazione del DTI a malattie del cervello
Il confronto dei dati DTI longitudinale richiede un allineamento / registrazione di dati di un oggetto tra l'altro. In tale contesto, la conservazione delle informazioni direzionale è necessario (cioè rotazione del tensore di diffusione durante trasformazioni affini). Possibili applicazioni a patologie neurodegenerative sono stati riportati in precedenza (ad esempio 18,19).
DTI è stato stabilito come uno strumento tecnico non invasivo robusto per studiare in vivo neuropathollogia di WM tratti neuronali (es. 11,20,21,22). Metrica quantitativa del processo di diffusione DTI basati, ad esempio il FA, hanno già dimostrato di essere indicatori sensibili per studiare una vasta gamma di WM patologie, come ad esempio corsa 20, sclerosi multipla 23, sclerosi laterale amiotrofica 24, 25, morbo di Alzheimer 26 , e molti altri disturbi WM 27,28.
Ulteriormente, DTI con FT può essere utilizzato per identificare WM tratti 23. Questa tecnica, mentre ancora non è in uso clinico di routine, sta emergendo come un potente strumento per la valutazione delle anomalie pathway-specifici nella malattia neurologica. All'interno dei tratti individuati, vari indici MRI quantitativi derivati dalla DTI e acquisizioni aggiuntive (ad esempio immagini T2 e / o trasferimento di magnetizzazione (MT) per immagini) che sono anatomicamente coregistrate ai dati DTI potrebbe essere misurata. Con il presente documento, ogni indice può essere calculgestiti come una funzione della posizione all'interno del tratto, riferendosi a trame raffiguranti loro variazione spaziale come profili tratto.
Nei seguenti, scansioni DTI umani che sono stati eseguiti su 1,5 Tesla MRI scanner (Siemens Medical, Erlangen, Germania) sono stati utilizzati per studiare il potenziale delle varie tecniche di analisi per la rilevazione di anomalie della sostanza bianca in gruppi di pazienti, così come negli individui. Dopo un controllo qualità automatizzato per l'eliminazione di volumi moto-corrotti e volumi con altri tipi di manufatti, procedure standardizzate postprocessing preparano i dati DTI per l'analisi consecutiva. I diversi approcci di analisi saranno illustrati nel seguito, vale a dire in primo luogo, tutto il cervello in base statistica spaziale (WBSS), in secondo luogo, FT, e la terza, statistiche anisotropia frazionale Tractwise (TFAS). WBSS è un metodo che viene eseguito in analogia con morfometria voxel-based (VBM), che di solito è conosciuto come morfometria voxel-based / statistiche sui dati DTI (VBM / DTI) . VBM è un metodo che viene eseguito originariamente sulle immagini a contrasto in cui le differenze di contrasto nelle scansioni separati devono essere risolte mentre WBSS è un metodo che utilizza il confronto voxelwise di un parametro fisico. Pertanto, sebbene algoritmicamente simile, una terminologia che è differenziando WBSS e VBM sarà utilizzata nel seguito.
Access restricted. Please log in or start a trial to view this content.
Protocollo
Analisi Metodi: Pre-e post-elaborazione
Il compito del seguente protocollo è quello di analizzare le proprietà di diffusione voxelwise entro tratti di materia bianca che potrebbe essere - a causa del rilevamento voxelwise - sia isotropo o anisotropo, con conseguente tensori di diffusione prolate o oblato per i rispettivi voxel. La parametrizzazione dei tensori voxel viene usato sia per il calcolo di FA-mappe o l'identificazione di fibertracts (Figura 1).
Al fine di ottenere i risultati delle analisi, come indicato nel seguito, utilizzare il pacchetto software Tensor Imaging and Fiber tracking (TIFT) 17. TIFT fornisce strumenti di analisi per i seguenti requisiti:
- analisi in termini di DTI metriche, ad esempio FA-mappe,
- normalizzazione stereotassica
- confronto di gruppo in termini di FA o altre metriche DTI
- diversi approcci di analisi del FT
- FT sul gruppo media DTI dati e l'analisi statistica corrispondente.
Queste caratteristiche consentono una serie di analisi in un unico ambiente software 17,29,30,31. Il software TIFT è costantemente in fase di sviluppo di nuove opzioni di analisi di dati DTI.
La figura 2 fornisce una panoramica schematica come analizzare i dati DTI a livello di gruppo dopo la normalizzazione spaziale da due approcci complementari, vale a dire sia per WBSS e da TFAS per ottenere finalmente le differenze tra i campioni sottoposti a livello di gruppo, ad esempio cervelli malati rispetto a controlli sani. Qui, WBSS mira a una rilevazione imparziale voxelwise di aree con differenze a livello di gruppo, mentre TFAS si basa su fibertracts predefiniti; le TFAS partire aree può sia essere scelto liberamente o può essere derivata dai risultati WBSS (`hotspot` di alterato significativamente FA).
Individuale confronto longitudinale del FA-mappe è eseguita da DATECdifferenze ting in FA-mappe di misurazioni a diversi intervalli di tempo dopo affine allineamento stereotassico (Figura 2).
- Controllo di qualità (QC), compresa la correzione per le direzioni di gradiente corrotti
In caso di disturbi del movimento durante l'acquisizione, vale a dire in caso di volumi danneggiati, con un incremento SNR si ottiene omettendo singole direzioni gradiente (GD) per il calcolo tensoriale. A tal fine, un controllo di qualità (QC) algoritmo 32 è stato sviluppato. In breve, per le scansioni che conteneva danneggiati volumi, con un aumento SNR è ottenuto omettendo singole direzioni gradiente uno alla volta prima stima tensore: per ogni GD, la varianza ponderata è calcolata da tutte le direzioni rimanenti nella sequenza per ponderazione l'angolo in che differivano dal indice GD.- Eseguire una correzione artefatto rilevando GD con almeno una fetta mostrando ridotta intensità, cioè artefatti di movimento causate da Su spontaneo movimento bject (figura 3, pannello superiore). Per qualsiasi volume ponderato diffusione, calcolare l'intensità media per ogni fetta e confrontare l'intensità con la stessa fetta in tutti gli altri volumi utilizzando un approccio di media ponderata - il fattore di ponderazione è il prodotto scalare di due vettori di GD
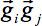 :
: 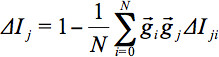
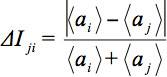
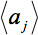 denota l'intensità media aritmetica della fetta sotto osservazione e427eq12.jpg "/> una fetta di confronto. La deviazione intensità relativa media
denota l'intensità media aritmetica della fetta sotto osservazione e427eq12.jpg "/> una fetta di confronto. La deviazione intensità relativa media 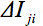 è ponderato per il prodotto scalare della GD. Pertanto, al fine di definire un parametro globale:
è ponderato per il prodotto scalare della GD. Pertanto, al fine di definire un parametro globale: 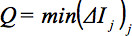
riflette il minimo di confronti slicewise di tutte le sezioni. - Se Q è sotto una certa soglia (nell'esempio, una soglia di 0,8 viene utilizzato per questo scopo), eliminare tale intero volume, o GD. Una soglia di 0,8 è considerata una soluzione stabile 32. Figura 3 illustra artefatti movimento visibile in ricostruzioni sagittali e rilevato dall'algoritmo QC. In questo esempio, rispetto al numero totale di GD (punti blu in figura 3c), 17 erano sotto la linea rossa che corrisponde a Q = 0.8 e should essere eliminato. Un esempio di un volume statistiche di eliminazione di un intero studio è presentata nella Figura 3d. In questo studio esemplare, dati DTI di 29 soggetti presintomatici HD sono stati confrontati con i dati DTI di 30 controlli. Ulteriori dettagli di questo algoritmo sono presentati in 32, 33.
- Eseguire una correzione artefatto rilevando GD con almeno una fetta mostrando ridotta intensità, cioè artefatti di movimento causate da Su spontaneo movimento bject (figura 3, pannello superiore). Per qualsiasi volume ponderato diffusione, calcolare l'intensità media per ogni fetta e confrontare l'intensità con la stessa fetta in tutti gli altri volumi utilizzando un approccio di media ponderata - il fattore di ponderazione è il prodotto scalare di due vettori di GD
- Pre-elaborazione e la normalizzazione spaziale
- Eseguire la correzione della corrente parassite indotte distorsioni geometriche dei dati di imaging echo-planari imposta con il metodo proposto da 34.
- Per la normalizzazione stereotassica, creare uno studio-specifica (b = 0) - modello e un FA-modello come descritto in precedenza 17,28,31. In sostanza, una normalizzazione stereotassica non lineare completo consiste di tre componenti di deformazione. Conseguentemente, il risultante tensore di diffusione
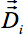 di ciascun voxel i ha di essere rotantied. secondo tutte le rotazioni elencati sopra (Figura 4):
di ciascun voxel i ha di essere rotantied. secondo tutte le rotazioni elencati sopra (Figura 4): - La Figura 4a mostra una trasformazione cervello rigida per allineare i sistemi di coordinate di base. La rotazione
 risultante dalla allineando al telaio coordinate di base deve essere applicata
risultante dalla allineando al telaio coordinate di base deve essere applicata 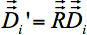
- Figura 4b mostra una deformazione lineare secondo punti di riferimento. I componenti degli autovettori
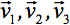 essere adattato secondo i sei parametri di normalizzazione di S (a seconda della regione del cervello s a,, a = 1 ... 6) della deformazione lineare.
essere adattato secondo i sei parametri di normalizzazione di S (a seconda della regione del cervello s a,, a = 1 ... 6) della deformazione lineare.
v w, j '' '= S a v w, j'''
w = 1,2,3 e j = x, y, z. - La figura 4c mostra una normalizzazione non lineare equalizzazione differente forma del cervello non lineari. Gli spostamenti vettore 3D sono differenti per ciascun voxel portando a una trasformazione separato per ciascun voxel dell'array voxel 3-D
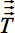 ). Trigonometria standard fornisce una matrice di rotazione indipendentemente per ciascun voxel, risultante dal vettore 3D sposta sui concetti del 16 al fine di preservare le relazioni fra direzionali autovettori di voxel neighbored. Così, diversi turni di due voxel neighbored provocano rotazioni dei corrispondenti autovettori. Utilizzare le matrici di dilatazione per l'allineamento del tensore
). Trigonometria standard fornisce una matrice di rotazione indipendentemente per ciascun voxel, risultante dal vettore 3D sposta sui concetti del 16 al fine di preservare le relazioni fra direzionali autovettori di voxel neighbored. Così, diversi turni di due voxel neighbored provocano rotazioni dei corrispondenti autovettori. Utilizzare le matrici di dilatazione per l'allineamento del tensore 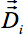 di ciascun voxeli voxel circostanti.
di ciascun voxeli voxel circostanti. 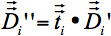
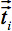 sono le componenti di
sono le componenti di 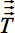
- La Figura 4a mostra una trasformazione cervello rigida per allineare i sistemi di coordinate di base. La rotazione
- Dopo questa procedura di normalizzazione individuale (step (i) - DTI-dati I 0), utilizzare tutti i singoli dati DTI imposta per la creazione di uno studio specifico (b = 0) - modello e una FA-template (passo (ii) - i modelli di T 1). Come la registrazione non affine a un FA-template ha il vantaggio che fornisce più contrasto rispetto a (b = 0) 10 immagini, definire un FA-template mediando tutti derivati singolarmente FA-mappe dei pazienti e dei controlli.
- In una seconda fase, seguendo le idee di base del Ashburner e Frisanco 35, eseguire un MNI normalizzazione non lineare (fase (iii)) dei dati DTI imposta, riducendo al minimo la mancata corrispondenza tra intensità regionali del FA-map da montare e di il FA-modello secondo le differenze al quadrato (X 2) - in questo modo, si ottiene DTI dati I 1.
- Sulla base di questi dati, i nuovi modelli di T 2 sono derivati (passo (iv)). Ripetere questo processo iterativo fino a quando la correlazione tra individuo FA-mappe e tegli FA-modello è> 0,7. Di solito questo viene raggiunto dopo due iterazioni.
- Intere statistica spaziale del cervello a base di
I seguenti passaggi 1.3.1 fino a 1.3.5 vengono rappresentati schematicamente nella figura 5b.- Calcolare FA-mappe da dati DTI normalizzati rispetto alla procedura di normalizzazione di 1.2. per conservare informazioni direzionali (fase (i)).
- Come passo di pre-elaborazione prima di confronto statistico voxelwise, applicare un filtro di smoothing (passo (ii)) per l'individuo normalizzato FA-mappe. Per la lisciatura, il fatto che la dimensione del filtro influenza i risultati delle analisi DTI dati 36 richiede l'applicazione del teorema filtro adattato che stabilisce che la larghezza del filtro utilizzato per elaborare i dati dovrebbe essere adattata alle dimensioni della differenza attesa, come dettagliato in applicazioni precedenti ai dati DTI di pazienti con malattie neurodegenerative (ad esempio 28).
- Eseguire statistico compArison tra i gruppi di pazienti e il corrispondente gruppo di controllo voxelwise di Student t-test, cioè confrontare i valori di FA dei pazienti 'FA-mappe con i valori di FA dei controlli' FA-mappe, per ogni voxel separatamente (passo (iii )). Valori di FA sotto 0.2 non sono considerati per il calcolo in quanto la materia grigia corticale presenta valori di FA fino a 0,2 37.
- I risultati statistici devono essere corretti per confronti multipli usando la-scoperta-di falsi (FDR) algoritmo a p <0.05 38 (passo (iv)). Ulteriore riduzione dell'errore alfa deve essere eseguita da un algoritmo di correlazione spaziale (clustering - fase (v)), che ha eliminato voxel isolate o piccoli gruppi isolati di voxel nella gamma di dimensioni del kernel smoothing, portando ad una dimensione di cluster soglia di 512 voxel.
- Per visualizzare i risultati su uno sfondo morfologico (passo (v)), normalizzare i D 3-T1 dati ponderati imposta di spazio e media MNI aritmeticamente. Eseguire questa normalizzazione pROCEDURA mediante l'uso di un modello di studi specifici in analogia alla normalizzazione applicato ai dati di DTI insiemi 17.
La figura 6 mostra i risultati di tutta la statistica spaziale cervello-based (WBSS) dei pazienti vs controlli di SLA. Figura 6a mostra il massimo locale di valori di FA sono diminuiti in un sagittale, coronar e vista assiale (thresholded a p <0.01, corretti per multiple i confronti). Figura 6b mostra FT proiettivo con punti di partenza nel tratto corticospinale utilizzato come base per TFAS. Figura 6c mostra le differenze di gruppo in FA-mappe rilevati dal cervello complesso basate statistica spaziale (WBSS) tra un campione di pazienti affetti da SLA e controlli appaiati in una visualizzazione slicewise.
- Statistiche di anisotropia frazionaria tractwise trattografia e (TFAS)
La Figura 7 illustra il processo di FT basato sul gruppo compreso TFAS come descritto in 1.4.1 fino a 1.4.4.- Al fine di applicare a base di gruppo algoritmi FT, generare una media di dati DTI imposta dai "dati e dai controlli dei pazienti dati insieme secondo i metodi descritti in precedenza 17. Questa media richiede un trattamento accurato delle informazioni orientazionale che si conserva durante il processo di normalizzazione secondo tecniche descritte da 16 - per i dettagli vedere 30.
- Eseguire trattografia in medi insiemi di dati DTI di gruppi di soggetti mediante l'applicazione di una tecnica di semplificare il monitoraggio 31. Identificare i punti di semi definiti manualmente adiacenti al massimi locali da tutto il analisi FA cervello a base che sono la base per l'analisi FT consecutivo. Dopo l'identificazione dei semi, eseguire trattografia e definire i voxel delle fibre, così definita una maschera di gruppo-specifico per il seguente TFAS 30.
- Al fine di quantificare i risultati trattografia, applicare la tecnica di TFAS utilizzando thposta in fibra di tratti che sono stati creati su dati DTI mediato insiemi di tutti i soggetti di ciascun gruppo (i dati del paziente e dati di controllo insieme) per la selezione dei voxel che contribuiscono a un confronto tra i pazienti e dei controlli 'FA-mappe.
- Considerare tutti i voxel risultanti con un valore di FA sopra 0.2 per l'analisi statistica di Student t-test.
- Se lo si desidera, la tecnica TFAS potrebbe essere applicato a tutte le metriche derivate DTI, come la diffusività media (MD), anisotropia radiale, anisotropia assiale, ecc (per un esempio, vedere 28).
- I risultati vengono visualizzati su un fondo morfologico costituito dai MNI-normalizzati 3 D-set T1 pesate dati
Access restricted. Please log in or start a trial to view this content.
Risultati
1. Controllo di qualità e la correzione per i danneggiati di pendenza direzioni in applicazione ai dati dei pazienti con disturbi ipercinetici
Come esempio per l'effetto dell'applicazione del QC e successiva esclusione del volume (come conseguenza dalla correzione per i danneggiati GD), la Figura 8 mostra differenze nel cervello intero statistica spaziale based con e senza volume esclusione di confronto gruppo di 29 malattia di premanifest Huntington soggetti di età v...
Access restricted. Please log in or start a trial to view this content.
Discussione
Interindividuale media dei dati DTI può essere ottenuto rispetto alla ampiezza diffusione (mediante l'uso di informazioni FA) e direzione diffusione (basato su FT), rispettivamente. Una media di FA mappe consente il raffronto statistico dei gruppi di soggetti da WBSS e TFA. Questo quadro metodologico fornisce una introduzione alle tecniche DTI con inter-soggetto della media e confronto di gruppo. Normalizzazione stereotassica e confronto di mappe FA a livello di gruppo consente più possibilità di quantificare le ...
Access restricted. Please log in or start a trial to view this content.
Divulgazioni
Gli autori non hanno nulla da rivelare.
Riconoscimenti
Alcune parti di questo lavoro, vale a dire lo studio sul controllo di qualità e la correzione per i danneggiati di pendenza direzioni in applicazione ai dati dei pazienti con disturbi ipercinetici, sono state supportate dalla rete HD Europea (progetto EHDN 070). Le scansioni MRI in questa determinata studio sono stati acquisiti come parte del London sito TRACK-HD coorte.
Access restricted. Please log in or start a trial to view this content.
Materiali
| Name | Company | Catalog Number | Comments |
| MR scanner | Siemens 1.5 T Magnetom Symphony | ||
| analysis software | TIFT - Tensor Imaging and Fiber Tracking |
Riferimenti
- Moseley, M. E., Cohen, Y., et al. Diffusion-weighted MR imaging of anisotropic water diffusion in cat central nervous system. Radiology. 176, 439-445 (1990).
- Mori, S., van Zijl, P. C. M. Fiber tracking: principles and strategies - a technical review. NMR Biomed. 15, 468-480 (2002).
- Basser, P. J., Mattiello, J., LeBihan, D. MR Diffusion Tensor Spectroscopy and Imaging. Biophys J. 66, 259-267 (1994).
- Mattiello, J., Basser, J. P., Le Bihan, D. Analytical expression for the b-matrix in NMR diffusion imaging and spectroscopy. J. Magn. Reson. A. 108, 131-141 (1994).
- Pierpaoli, C., Basser, P. J. Toward a quantitative assessment of diffusion anisotropy. Magn. Reson. Med. 36, 893-906 (1996).
- Pajevic, S., Pierpaoli, C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: application to white matter fiber tract mapping in the human brain. Magn. Reson. Med. 42, 526-540 (1999).
- Le Bihan, D., Mangin, J. F., et al. Diffusion tensor imaging: concepts and applications. J. Magn. Reson. Imaging. 13, 534-546 (2001).
- Conturo, T. E., Lori, N. F., et al. Tracking neuronal fibre pathways in the living human brain. Proc. Natl. Acad. Sci. U.S.A. 96, 10422-10427 (1999).
- Lori, N. F., Akbudak, E. Diffusion tensor fibre tracking of human brain connectivity: aquisition methods, reliability analysis and biological results. NMR Biomed. 15, 494-515 (2002).
- Smith, S. M., Jenkinson, M., et al. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 31, 1487-1505 (2006).
- Agosta, F., Pagani, E., et al. Assessment of white matter tract damage in patients with amyotrophic lateral sclerosis: a diffusion tensor MR imaging tractography study. AJNR. Am. J. Neuroradiol. 31, 1457-1461 (2010).
- Talairach, J., Tournoux, P. Coplanar stereotaxic atlas of the human brain. , Thieme Medical. New York. (1988).
- Brett, M., Johnsrude, I. S., Owen, A. M. The problem of functional localization in the human brain. Nat. Rev. Neurosci. 3, 243-249 (2002).
- Collins, D. L., Neelin, P., Peters, T. M., Evans, A. C. Automatic 3-D intersubject registration of MR volumetric data in standardized Talairach space. J. Comput. Assist. Tomogr. 18, 192-205 (1994).
- Friston, K. J., Ashburner, J., Frith, C. D., Poline, J. -B., Heather, J. D., Frackowiak, R. S. J. Spatial registration and normalization of images. Human Brain Mapp. 2, 165-189 (1995).
- Alexander, D. C., Pierpaoli, C., Basser, P. J., Gee, J. C. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans. Med. Imaging. 20, 1131-1139 (2001).
- Müller, H. -P., Unrath, A., Ludolph, A. C., Kassubek, J. Preservation of Diffusion Tensor Properties during Spatial Normalization by use of Tensor imaging and Fiber Tracking on a Normal Brain Database. Phys. Med. Biol. 52, N99-N109 (2007).
- Likitjaroen, Y., Meindl, T., et al. Longitudinal changes of fractional anisotropy in Alzheimer's disease patients treated with galantamine: a 12-month randomized, placebo-controlled, double-blinded study. Eur. Arch. Psychiatry Clin. Neurosci. 262, 341-350 (2012).
- Zhang, Y., Schuff, N. Progression of white matter degeneration in amyotrophic lateral sclerosis: A diffusion tensor imaging study. Amyotroph. Lateral Scler. 12, 421-429 (2011).
- Pierpaoli, C., Barnett, A. Water diffusion changes in Wallerian degeneration and their dependence on white matter architecture. Neuroimage. 13, 1174-1185 (2001).
- Agosta, F., Valsasina, P., et al. Sensorimotor functional connectivity changes in amyotrophic lateral sclerosis. Cereb Cortex. 21, 2291-2298 (2011).
- Müller, H. -P., Unrath, A., Huppertz, H. J., Ludolph, A. C., Kassubek, J. Neuroanatomical patterns of cerebral white matter involvement in different motor neuron diseases as studied by diffusion tensor imaging analysis. Amyotroph Lateral Scler. 13, 254-264 (2012).
- Reich, D. S., Zackowski, K. M. Corticospinal tract abnormalities are associated with weakness in multiple sclerosis. Am. J. Neuroradiol. 29, 333-339 (2008).
- Abe, O., Yamada, H. Amyotrophic lateral sclerosis: Diffusion tensor tractography and voxel-based analysis. NMR Biomed. 17, 411-416 (2004).
- Sage, C. A., Peeters, R. R., Gorner, A., Robberecht, W., Sunaert, S. Quantitative diffusion tensor imaging in amyotrophic lateral sclerosis. Neuroimage. 34, 486-499 (2007).
- Preti, M. G., Baglio, F., et al. Assessing corpus callosum changes in Alzheimer's disease: comparison between tract-based spatial statistics and atlas-based tractography. PLoS One. 7, e35856(2012).
- Borroni, B., Brambati, S. M., et al. Evidence of white matter changes on diffusion tensor imaging in frontotemporal dementia. Arch. Neurol. 64, 246-251 (2007).
- Unrath, A., Müller, H. -P., Riecker, A., Ludolph, A. C., Sperfeld, A. D., Kassubek, J. Whole brain-based analysis of regional white matter tract alterations in rare motor neuron diseases by diffusion tensor imaging. Hum Brain Mapp. 31, 1727-1740 (2010).
- Müller, H. -P., Lulé, D., Unrath, A., Ludolph, A. C., Riecker, A., Kassubek, J. Complementary Image Analysis of Diffusion Tensor Imaging and 3-Dimensional T1-Weighted Imaging: White Matter Analysis in Amyotrophic Lateral Sclerosis. J. Neuroimaging. 21, 24-33 (2011).
- Müller, H. -P., Unrath, A., Sperfeld, A. D., Ludolph, A. C., Riecker, A., Kassubek, J. Diffusion tensor imaging and tractwise fractional anisotropy statistics: quantitative analysis in white matter pathology. Biomed. Eng. Online. 6, 42(2007).
- Müller, H. -P., Unrath, A., Riecker, A., Pinkhardt, E. H., Ludolph, A. C., Kassubek, J. Inter-subject variability in the analysis of diffusion tensor imaging at the group level: fractional anisotropy mapping and fiber tracking techniques. Magn. Reson. Imaging. 27, 324-334 (2009).
- Müller, H. -P., Glauche, V., et al. Stability of white matter changes related to Huntington's disease in the presence of imaging noise: a DTI study. PLoS Curr. 3, RRN1232(2011).
- Müller, H. -P., Süßmuth, S. D., Landwehrmeyer, G. B., Ludolph, A. C., Tabrizi, S. J., Klöppel, S., Kassubek, J. Stability effects on results of diffusion tensor imaging analysis by reduction of the number of gradient directions due to motion artifacts: an application to presymptomatic Huntington's disease. PLoS Curr. 3, RRN1292(2011).
- Shen, Y., Larkman, D. J., Counsell, S., Pu, I. M., Edwards, D., Hajnal, J. V. Correction of High-Order Eddy Current Induced Geometric Distortion in Diffusion-Weighted Echo-Planar images. Magn. Reson. Med. 52, 1184-1189 (2004).
- Ashburner, J., Friston, K. J. Nonlinear Spatial Normalization Using Basis Functions. Human Brain Mapping. 7, 254-266 (1999).
- Jones, D. K., Symms, M. R., Cercignani, M., Howard, R. J. The effect of filter size on VBM analyses of DT-MRI data. Neuroimage. 26, 546-554 (2005).
- Kunimatsu, A., Aoki, S., et al. The optimal trackability threshold of fractional anisotropy for diffusion tensor tractography of the corticospinal tract. Magn. Reson. Med. Sci. 3, 11-17 (2004).
- Genovese, C. R., Lazar, N. A., Nichols, T. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage. 15, 870-878 (2002).
- Cleaver, J. E. Defective repair replication of DNA in xeroderma pigmentosum. Nature. 218, 652-656 (1968).
- Anttinen, A., Koulu, L., et al. Neurological symptoms and natural course of xeroderma pigmentosum. Brain. 131, 1979-1989 (2008).
- Kassubek, J., Sperfeld, A. D. The cerebro-morphological fingerprint of a progeroid syndrome: white matter changes correlate with neurological symptoms in xeroderma pigmentosum. PLoS One. 7, e30926(2012).
- Canu, E., Agosta, F. The topography of brain microstructural damage in amyotrophic lateral sclerosis assessed using diffusion tensor MR imaging. AJNR. Am. J. Neuroradiol. 32, 1307-1314 (2011).
- Verstraete, E., Veldink, J. H., Hendrikse, J., Schelhaas, H. J., van den Heuvel, M. P., van den Berg, L. H. Structural MRI reveals cortical thinning in amyotrophic lateral sclerosis. J. Neurol. Neurosurg. Psychiatry. 83, 383-388 (2012).
- Hofer, S., Frahm, J. Topography of the human corpus callosum revisited- comprehensive fiber tractography using diffusion tensor magnetic resonance imaging. Neuroimage. 32, 989-994 (2006).
- Iwata, N. K., Kwan, J. Y., et al. White matter alterations differ in primary lateral sclerosis and amyotrophic lateral sclerosis. Brain. 134, 2642-2655 (2011).
- Kassubek, J., Ludolph, A. C., Müller, H. -P. Neuroimaging of motor neuron diseases. Ther. Adv. Neurol. Disord. 5, 119-127 (2012).
- Kassubek, J., Juengling, F. D. Multimodality functional neuroimaging. In: C. Stippich (Ed.): Clinical functional MRI - Presurgical functional neuroimaging. , Springer. Berlin/Heidelberg/New York. (2007).
- Stadlbauer, A., Buchfelder, M., Salomonowitz, E., Ganslandt, O. Fiber density mapping of gliomas: histopathologic evaluation of a diffusion-tensor imaging data processing method. Radiology. , 257-846 (2010).
- Stadlbauer, A., Hammen, T., et al. Differences in metabolism of fiber tract alterations in gliomas: a combined fiber density mapping and magnetic resonance spectroscopic imaging study. Neurosurgery. 71, 454-463 (2012).
- Staempfli, P., Jaermann, T., Crelier, G. R., Kollias, S., Valavanis, A., Boesiger, P. Resolving fiber crossing using advanced fast marching tractography based on diffusion tensor imaging. Neuroimage. 30, 110-120 (2006).
- Ehricke, H. H., Otto, K. M., Klose, U. Regularization of bending and crossing white matter fibers in MRI Q-ball fields Magn. Reson Imaging. 29, 916-926 (2011).
- Hirsch, J. G., Schwenk, S. M., Rossmanith, C., Hennerici, M. G., Gass, A. Deviations from the diffusion tensor model as revealed by contour plot visualization using high angular resolution diffusion-weighted imaging (HARDI). MAGMA. 16, 93-102 (2003).
- Lazar, M., Weinstein, D. M., et al. White matter tractography using diffusion tensor deflection. Human Brain Mapping. 18, 306-321 (2003).
- Reisert, M., Mader, I., Anastasopoulos, C., Weigel, M., Schnell, S., Kiselev, V. Global fiber reconstruction becomes practical. Neuroimage. 54, 955-962 (2011).
- Klein, A., Andersson, J. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage. 46, 786-802 (2009).
- Bammer, R. Basic principles of diffusion-weighted imaging. Eur. J. Radiol. 45, 169-184 (2003).
- Mohammadi, S., Keller, S. S. The influence of spatial registration on detection of cerebral asymmetries using voxel-based statistics of fractional anisotropy images and TBSS. PLoS One. 7, e36851(2012).
- Turner, M. R., Grosskreutz,, et al. Towards a neuroimaging biomarker for amyotrophic lateral sclerosis. Lancet Neurol. 10, 400-403 (2011).
- Müller, H. -P., Kassubek, J. Multimodal imaging in neurology - special focus on MRI applications and MEG. Synthesis Lectures in Biomedical Engineering. Enderle, J. D. 16, Morgan & Claypool Publishers. (2008).
- Douaud, G., Filippini, N., Knight, S., Talbot, K., Turner, M. R. Integration of structural and functional magnetic resonance imaging in amyotrophic lateral sclerosis. Brain. 134, 3470-3479 (2011).
- Kolind, S. H., Laule, C., et al. Complementary information from multi-exponential T2 relaxation and diffusion tensor imaging reveals differences between multiple sclerosis lesions. Neuroimage. 40, 77-85 (2008).
- Verma, R., Zacharaki, E. I. Multiparametric tissue characterization of brain neoplasms and their recurrence using pattern classification of MR images. Acad. Radiol. 15, 966-977 (2008).
Access restricted. Please log in or start a trial to view this content.
Ristampe e Autorizzazioni
Richiedi autorizzazione per utilizzare il testo o le figure di questo articolo JoVE
Richiedi AutorizzazioneEsplora altri articoli
This article has been published
Video Coming Soon