Zum Anzeigen dieser Inhalte ist ein JoVE-Abonnement erforderlich. Melden Sie sich an oder starten Sie Ihre kostenlose Testversion.
Method Article
Diffusion Tensor Magnetic Resonance Imaging in der Analyse von neurodegenerativen Erkrankungen
In diesem Artikel
Zusammenfassung
Diffusion Tensor Imaging (DTI) dient im wesentlichen als eine MRT-basiertes Tool zur Identifizierung In vivo Die Mikrostruktur des Gehirns und pathologischen Prozessen durch neurologische Störungen im weißen Hirnsubstanz. DTI-basierte Analysen erlauben für die Anwendung auf Erkrankungen des Gehirns sowohl auf Konzernebene als auch in Ein-Fach-Daten.
Zusammenfassung
Diffusion Tensor Imaging (DTI) Techniken geben Auskunft über die mikrostrukturellen Prozesse der weißen Hirnsubstanz (WM) in vivo. Die vorliegenden Anwendungen sind für Differenzen WM Beteiligung Muster in verschiedenen Erkrankungen des Gehirns, insbesondere neurodegenerativen Erkrankungen, unter Verwendung unterschiedlicher DTI Analysen im Vergleich zu entsprechenden Kontrollen untersucht werden.
DTI Datenanalyse in einem variate Weise durchgeführt wird, dh voxelwise Vergleich regionaler Diffusionsrichtung-Metriken wie fraktionierte Anisotropie (FA), zusammen mit Fiber Tracking (FT) durch fraktionierte Anisotropie tractwise Statistik (TFAS) auf Konzernebene um begleitet Unterschiede in FA entlang WM Strukturen zu identifizieren, die auf die Definition der regionalen Muster der WM Änderungen auf Gruppenebene. Transformation in einen stereotaktischen Raum Standard ist eine Voraussetzung für die Gruppe Studien und erfordert eine gründliche Datenverarbeitung d erhaltenirectional gegenseitigen Abhängigkeiten. Die vorliegenden Anträge zeigen optimiert technische Ansätze für diese Erhaltung der quantitativen und Richtungsangaben während räumliche Normalisierung in Datenanalysen auf Gruppenebene. Auf dieser Grundlage kann FT Techniken zur Gruppe gemittelt Daten angewendet werden, um Informationen Metriken quantifizieren, wie durch FT definiert. Darüber hinaus Anwendung der DTI Methoden, offenbaren dh Unterschiede in FA-Karten nach stereotaktischen Ausrichtung, in einer Längs-Analyse an einem einzelnen Gegenstand Basis Informationen über den Verlauf von neurologischen Erkrankungen. Weitere Qualitätsverbesserung DTI auf Ergebnisse im Vorlauf durch Anwendung einer kontrollierten Beseitigung von Gradientenrichtungen mit hohem Geräuschpegel erreicht werden.
Zusammenfassend wird DTI verwendet, um eine deutliche WM Pathoanatomie verschiedener Hirnerkrankungen durch die Kombination der gesamte Gehirn-basierte und Darm-basierte Analyse DTI definieren.
Einleitung
Diffusion-Tensor-Bildgebung im menschlichen Gehirn
Die weiße Substanz (WM) Verträge in das zentrale Nervensystem bestehen aus dicht gepackten Axone zusätzlich zu den verschiedenen Arten von Gliazellen und andere kleine Populationen von Zellen. Die axonale Membran sowie die gut ausgerichteten Protein-Fasern innerhalb eines Axon schränkt Wasserdiffusion senkrecht zur Faserorientierung, was zu anisotropen Diffusion von Wasser in Gehirn WM 1. Myelinscheiden um die Axone kann auch auf die Anisotropie beitragen sowohl für intra-und extrazelluläre Wasser 2.
Die quantitative Beschreibung dieser Anisotropie konnte durch Diffusion Tensor Imaging (DTI) nachgewiesen werden. DTI erzeugt Bilder von Geweben mit den lokalen mikrostrukturellen Eigenschaften von Wasser Diffusion gewichtet. Die Bild-Intensitäten an jeder Position gedämpft werden, abhängig von der Stärke und Richtung des sogenannten magnetischen Diffusionsgradienten (dargestellt inder B-Wert), als auch auf dem lokalen Mikrostruktur, in der das Wasser diffundieren 3, der Diffusionskoeffizient D einen Skalarwert:

Jedoch in Gegenwart von Anisotropie in WM kann die Diffusion nicht mehr durch einen einzelnen skalaren Koeffizienten charakterisiert werden, erfordert jedoch einen Tensor  die in erster Näherung beschreibt molekulare Beweglichkeit entlang jeder Richtung und Korrelation zwischen diesen Richtungen 4. Diffusion Anisotropie ist vor allem durch die Ausrichtung der WM in Nervenbahnen verursacht und ist durch seine Mikro-und makrostrukturelle Funktionen beeinflusst. Von den mikrostrukturellen Eigenschaften, erscheint intraaxonal Organisation des größten Einfluss auf Diffusionsanisotropie sein, neben der Dichte der Faser einnd Zelle Verpackung, dem Grad der Myelinisierung und einzelne Faser Durchmesser. In einem makroskopischen Maßstab, beeinflusst die Variabilität in der Ausrichtung aller WM Flächen in einem bildgebenden Voxel der Grad der Anisotropie 5.
die in erster Näherung beschreibt molekulare Beweglichkeit entlang jeder Richtung und Korrelation zwischen diesen Richtungen 4. Diffusion Anisotropie ist vor allem durch die Ausrichtung der WM in Nervenbahnen verursacht und ist durch seine Mikro-und makrostrukturelle Funktionen beeinflusst. Von den mikrostrukturellen Eigenschaften, erscheint intraaxonal Organisation des größten Einfluss auf Diffusionsanisotropie sein, neben der Dichte der Faser einnd Zelle Verpackung, dem Grad der Myelinisierung und einzelne Faser Durchmesser. In einem makroskopischen Maßstab, beeinflusst die Variabilität in der Ausrichtung aller WM Flächen in einem bildgebenden Voxel der Grad der Anisotropie 5.
In typischen DTI Messungen werden die Voxel Abmessungen in der Größenordnung von Millimetern. So ein Voxel enthält immer die gemittelten Daten der Wassermoleküle innerhalb der erfassten Volumen, das in der Regel erstreckt sich über mehrere Axone sowie die umliegenden Wassermoleküle. Trotz dieser Mehrwege-Umgebung DTI empfindlich auf die Orientierung des größten Hauptachse, die zum überwiegenden axonalen Richtung ausgerichtet ist, dh die axonale Beitrag dominiert das gemessene Signal 2.
DTI bietet zwei Arten von Informationen über die Eigenschaft des Wassers Diffusion: erstens die lageunabhängige Ausmaß Diffusionsanisotropie 5 und die zweite, die vorherrschende Richtung der Diffusion von Wasser in image Voxel, dh die Diffusion Ausrichtung 6.
Die aktuellen Protokolle sollen einen Rahmen von DTI Analyseverfahren zur quantitativen Vergleich der Fächergruppen auf Gruppenebene zu stellen, wie im folgenden beschrieben.
Quantifizierung der Diffusion Eigenschaften - Analyse Parameter
Die Elemente der Tensor durch Diffusion Gradienten entlang mindestens sechs nicht-kollinear und nicht koplanare Richtungen gemessen werden, so dass b (Gleichung 1) hat sich ein Tensor, wodurch Signaldämpfung
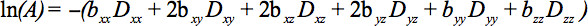
Diese Gleichung erfordert Bilanzierung von möglichen Wechselwirkungen zwischen Bildgebung und Diffusionsgradienten, die in orthogonalen Richtungen (cross Begriffe) angewendet werden, und sogar zwischen Abbildungsgradienten, die angewendet werdenin 4 senkrechten Richtungen.
Der zweite Rang-Diffusions-Tensor  immer diagonalisierten so dass nur drei Nicht-Null-Elemente entlang der Hauptdiagonalen der Tensor, dh die Eigenwerte (
immer diagonalisierten so dass nur drei Nicht-Null-Elemente entlang der Hauptdiagonalen der Tensor, dh die Eigenwerte ( 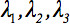 ). Die Eigenwerte spiegeln die Form oder Konfiguration des Ellipsoids. Die mathematische Beziehung zwischen der Haupt-Koordinaten des Ellipsoids und Laborsystem wird durch die Eigenvektoren beschriebenen
). Die Eigenwerte spiegeln die Form oder Konfiguration des Ellipsoids. Die mathematische Beziehung zwischen der Haupt-Koordinaten des Ellipsoids und Laborsystem wird durch die Eigenvektoren beschriebenen 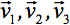
Da es einige Herausforderungen bei der Anzeige Tensor Daten sind, hat sich das Konzept der Diffusion Ellipsoide wurden 3 vorgeschlagen. Die Eigendiffusivities dieser Ellipsoids stellen die eindimensionale Diffusionskoeffizienten in der Hauptrichtung des Diffusionskoeffizienten des Mediums, dh die Hauptachse des Ellipsoids stellt die Haupt-Diffusion in Richtung der Voxel, welche die Richtung der Fasern zusammenfällt, während die Exzentrizität des Ellipsoids liefert Informationen über die Grad der Anisotropie und ihre Symmetrie. Daher könnte Diffusionsanisotropie Metriken wie der fraktionierten Anisotropie (FA) 7 definiert werden.

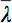 ist das arithmetische Mittel aller Eigenwerte.
ist das arithmetische Mittel aller Eigenwerte.
Ein weiterer Ansatz besteht darin, die Hauptrichtung der Diffusions-Tensor-WM nutzen, um die Konnektivität des Gehirns ansprechen, entsprechend der tractography approach denen die Absicht hat, zu untersuchen, welche Teile des Gehirns sind miteinander verbunden. Unter der Annahme, dass die Orientierung der Hauptbestandteil der Diffusions-Tensor die Ausrichtung der dominante axonale Verträge darstellt, wird ein 3-D-Vektor-Feld vorgesehen, in dem jeder Vektor repräsentiert die Faserorientierung. Derzeit gibt es verschiedene Ansätze zur WM Traktate, die in zwei Typen unterteilt werden konnte rekonstruieren: Die erste Kategorie ist on line Ausbreitung Algorithmen mit dem lokalen Tensor Informationen für jeden Schritt der Faser-Trakt Ausbreitung 2,8,9 basiert. Die zweite Kategorie ist auf globale Energieminimierung basieren, die energetisch günstigste Weg zwischen zwei WM Regionen, die sich in den Ansatz-Trakt-basierten räumlichen Statistik finden (TBSS) 10, die in anderen Algorithmen wie tractwise fraktionierte Anisotropie Statistiken (TFAS verwendet wurde - siehe Protokoll Text, Abschnitt 2.4)..
Transformation in stereotaktischen Standard Raum
Wie in anderen entwickelten MRI-Verfahren verfolgen DTI-und FT-basierte Studien im klinischen Kontext, das ultimative Ziel zu einzelnen Patienten Gehirnmorphologie kategorisieren, um die diagnostischen Prozess auf einige Diskriminierung metrisch 11 Basis zu erleichtern. Studium an der Gruppenebene sind die meisten relevant, wenn die gemeinsame klinische Phänotyp soll darauf zurückzuführen sein, zu einem oder mehreren spezifischen Hirnregionen oder einem bestimmten neuroanatomical Netzwerk beschädigen. Hier, im Durchschnitt der Ergebnisse für verschiedene Themen ist, um gemeinsame Muster der mikrostrukturellen Veränderungen beurteilen nützlich. Jede einzelne Gehirn muss in stereotaktischen Raum übertragen werden, so dass in einem zweiten Schritt das arithmetische Mittelung der Ergebnisse in einem Voxel-für-Voxel Ebene möglich ist. Räumliche Normalisierung für arithmetische Mittelung der Ergebnisse aus verschiedenen Fächern erhalten wird, um das Signal-zu-Rausch-Verhältnis (SNR) zu verbessern und um einen Vergleich der Proben von Patienten und cont durchzuführen erlaubtrols, um den Rechenaufwand Pathoanatomie einer bestimmten Erkrankung zu analysieren, beispielsweise eine neurodegenerative Erkrankung, die mit der Zuweisung einer bestimmten Gehirn-System zugeordnet ist.
Der frühe Ansatz der Normalisierung einer standardisierten stereotaktischen Raum von 12 schlug eine Transformations-Algorithmus zu einem Standard-Atlas, der die Identifikation von verschiedenen Sehenswürdigkeiten und Gehirn stückweise Skalierung des Gehirns Quadranten. Heutzutage nutzen die meisten der fortgeschrittenen MRI Datenanalyse Pakete Normalisierung des Montreal Neurological Institute (MNI) stereotaktischen Raum 13. Für diese Transformation wurden halbautomatische und automatische Gehirn Registrierung Algorithmen mit Studie Templates 14,15 entwickelt. In DTI hat besondere Aufmerksamkeit zu ziehen, um die Richtungs-Informationen während der Prozess der Normalisierung 16,17 bewahren. Die Anwendung der räumlichen Transformationen auf DT-MRT-Bilder, die sind für die räumliche Normalisierung erforderlichSammlungen von Datensätzen ist, im Gegensatz zum Verziehen skalare Bilder, dadurch gekennzeichnet, dass die Orientierung DTs Informationen, die wiederum durch die Transformation beeinträchtigt enthalten kompliziert. Dieser Effekt muss berücksichtigt werden, um die anatomische Korrektheit der transformierten Abbildung zu gewährleisten. Hier werden Techniken zum Aufbringen affine Transformationen DTI Datensätze vorgestellt.
Anwendung der DTI von Hirnerkrankungen
Der Vergleich der Längs-DTI-Daten erfordert eine Ausrichtung / Anmeldung eines Subjekts Daten untereinander. In diesem Zusammenhang ist die Erhaltung der gerichteten notwendigen Informationen (dh Drehung der Diffusions-Tensor während affine Transformationen). Mögliche Anwendungen zu neurodegenerativen Erkrankungen wurden bisher (zB 18,19) berichtet.
DTI hat als robustes nicht-invasive technisches Werkzeug wurde gegründet, um in vivo zu untersuchen Neuropathollogie der WM neuronalen Bahnen (zB 11,20,21,22). DTI-basierte quantitative Metrik der Diffusion, zB der FA, haben bereits gezeigt, dass sensible Marker für das Studium einer Vielzahl von WM Erkrankungen, wie Schlaganfall 20, Multiple Sklerose 23, amyotrophe Lateralsklerose 24, 25, Alzheimer-Krankheit 26 und verschiedene andere Störungen WM 27,28.
Darüber hinaus können mit DTI FT zur Identifizierung WM Traktate 23 werden. Diese Technik, die zwar noch nicht in die routinemäßige klinische Anwendung wird als ein mächtiges Instrument für die Beurteilung der Weg-spezifische Anomalien in neurologische Erkrankung entstehen. Innerhalb der identifizierten Flächen, verschiedene quantitative MRI Indizes von DTI und Akquisitionen (zB T2-gewichtete Bilder und / oder Magnetisierung Übertragung (MT)-Bildgebung) abgeleitet, sind anatomisch koregistrierten den DTI-Daten gemessen werden konnte. Dabei könnte jeder Index sein calculATED als eine Funktion der Position innerhalb der Fläche, die sich auf Parzellen Darstellung der räumlichen Variation als Trakt Profile.
In den folgenden, menschliche DTI Scans, die auf 1.5 durchgeführt wurden Tesla MRI-Scannern (Siemens Medical, Erlangen, Deutschland) wurden verwendet, um das Potenzial der verschiedenen Analyse-Techniken zum Nachweis von Anomalien der weißen Substanz in Patientengruppen sowie bei Personen zu untersuchen. Nach einer automatisierten Qualitätskontrolle für die Beseitigung der Bewegung-beschädigten Bände und Volumina mit anderen Arten von Artefakten, bereiten standardisierten Verfahren Nachbearbeitung die DTI-Daten für die fortlaufende Analyse. Verschiedene Ansätze Analyse werden im Folgenden dargestellt werden, dh es wird zuerst gesamten Gehirns räumlichen Statistik (WBSS), zweiten, FT und drittens Tractwise fraktionierte Anisotropie Statistiken (TFAS). WBSS ist eine Methode, die in Analogie zu Voxel-basierte Morphometrie (VBM), die in der Regel als Voxel-basierte Morphometrie / Statistiken über DTI-Daten (VBM / DTI) ist bekannt, läuft . VBM ist eine Methode, die ursprünglich läuft auf kontrastreiche Bilder, wo hingegen Unterschiede in separaten Scans müssen gelöst werden, während WBSS ist eine Methode, die voxelwise Vergleich eines physikalischen Parameters verwendet. Obwohl also algorithmisch ähnlich wird eine Terminologie, die Differenzierung und WBSS VBM wird im folgenden verwendet werden.
Access restricted. Please log in or start a trial to view this content.
Protokoll
Analyse-Methoden: Pre-und Postprocessing
Die Aufgabe des folgenden Protokolls ist die Diffusion Eigenschaften innerhalb der weißen Substanz, die sein könnte voxelwise analysieren - aufgrund der voxelwise Erkennung - entweder isotrope oder anisotrope, was prolate oder Oblate Diffusion Tensor für die jeweiligen Voxel. Die Parametrierung der Voxel Tensoren wird entweder für die Berechnung des FA-Karten oder die Identifizierung von fibertracts (Abbildung 1).
Um Analyseergebnisse zu erhalten, wie im folgenden Beispiel gezeigt, verwenden Sie das Software-Paket Tensor Imaging und Fiber Tracking (Tift) 17. Tift bietet Analyse-Tools für die folgenden Anforderungen erfüllen:
- Analyse in Bezug auf die DTI-Metriken, wie zB FA-Karten,
- stereotaktischen Normalisierung
- Group-Vergleich hinsichtlich der FA oder andere Metriken DTI
- Analyse verschiedener Ansätze der FT
- FT auf Gruppe gemittelt DTI und der entsprechenden statistischen Analyse.
Diese Merkmale ermöglichen eine Vielzahl von Analysen in einem Software-Umgebung 17,29,30,31. Die Tift Software ist ständig in der Entwicklung für neue Möglichkeiten in der DTI Datenanalyse.
Abbildung 2 gibt einen schematischen Überblick, wie DTI Daten auf Gruppenebene analysieren nach räumlichen Normalisierung von zwei komplementären Ansätzen, sowohl durch WBSS und TFAS dh um schließlich Unterschiede zwischen Subjekt Proben auf Gruppenebene, zB kranken Gehirnen im Vergleich zu gesunden Kontrollpersonen. Hier soll WBSS bei einer voxelwise unvoreingenommene Erkennung von Bereichen mit Unterschieden auf Gruppenebene, während TFAS auf vordefinierte fibertracts beruht; die TFAS ab Bereiche können entweder frei gewählt werden oder sich aus den WBSS Ergebnisse (`` Hotspots von abgeleitet werden wesentlich verändert FA).
Einzelne Längs Vergleich der FA-Karten ist vom UVEK durchgeführtting Unterschiede in FA-Karten von Messungen an verschiedenen Zeitpunkten nach der stereotaktischen affine Ausrichtung (Abbildung 2).
- Qualitäts-Check (QC) einschließlich Korrektur für beschädigte Gradientenrichtungen
Im Falle von Störungen während der Bewegung des Erwerbs, dh im Falle von beschädigten Datenträgern wird ein SNR Steigerung durch Weglassen einzigen Gradientenrichtungen (GD) für Tensor Berechnung erhalten. Zu diesem Zweck wurde eine Qualitätskontrolle (QC)-Algorithmus 32 entwickelt. Kurz gesagt, für Scans, die Bände beschädigt enthalten ist, wird eine Erhöhung SNR durch Auslassen einzelnen Gradientenrichtungen ein zu einer Zeit vor dem Tensor Schätzung erreicht: Bei jeder GD, die gewichtete Varianz aus den restlichen Richtungen in der Sequenz durch eine Gewichtung mit dem Winkel in der Computertomographie denen sie sich von dem Index GD.- Führen Sie ein Artefakt Korrektur durch Erfassen GD mit mindestens einer Scheibe zeigt verminderte Intensität, dh Bewegungsartefakte durch spontane su verursacht bject Bewegung (Abbildung 3, oben). Für jede diffusionsgewichtete Volumen, berechnen Sie die mittlere Intensität für jede Scheibe und vergleichen Sie die Intensität mit der gleichen Scheibe in allen anderen Datenträger mithilfe einer gewichteten durchschnittlichen Ansatz - der Gewichtungsfaktor ist das Skalarprodukt von Vektoren von zwei GD
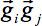 :
: 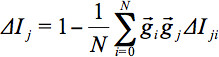
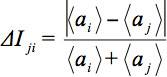
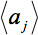 zeigt die arithmetische mittlere Intensität der Scheibe unter Beobachtung und427eq12.jpg "/> eine Scheibe zum Vergleich. Die relative mittlere Intensität Abweichung
zeigt die arithmetische mittlere Intensität der Scheibe unter Beobachtung und427eq12.jpg "/> eine Scheibe zum Vergleich. Die relative mittlere Intensität Abweichung 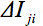 durch das Skalarprodukt der GD gewichtet. Somit wird, um einen globalen Parameter definieren:
durch das Skalarprodukt der GD gewichtet. Somit wird, um einen globalen Parameter definieren: 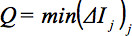
spiegelt die mindestens slicewise Vergleiche aller Scheiben. - Wenn Q unter einem bestimmten Schwellenwert (in diesem Beispiel ein Grenzwert von 0,8 ist für diesen Zweck verwendet werden), zu beseitigen, die gesamte Volumen oder GD. Ein Schwellenwert von 0,8 wird als eine stabile Lösung 32. 3 veranschaulicht Bewegungsartefakte sichtbar sagittalen Rekonstruktionen und von dem QC-Algorithmus. In diesem Beispiel, aus der Gesamtzahl der GD (blaue Punkte in Abb. 3c), 17 unterhalb der roten Linie, die zu Q = 0,8 entspricht und should beseitigt werden. Ein Beispiel für ein Volumen Beseitigung Statistiken für eine ganze Studie ist in Abbildung 3d dargestellt. In dieser exemplarischen Studie wurden Daten von 29 DTI präsymptomatischen HD Untertanen DTI Daten von 30 Kontrollpersonen verglichen. Weitere Einzelheiten dieses Algorithmus sind in 32, 33 dargestellt.
- Führen Sie ein Artefakt Korrektur durch Erfassen GD mit mindestens einer Scheibe zeigt verminderte Intensität, dh Bewegungsartefakte durch spontane su verursacht bject Bewegung (Abbildung 3, oben). Für jede diffusionsgewichtete Volumen, berechnen Sie die mittlere Intensität für jede Scheibe und vergleichen Sie die Intensität mit der gleichen Scheibe in allen anderen Datenträger mithilfe einer gewichteten durchschnittlichen Ansatz - der Gewichtungsfaktor ist das Skalarprodukt von Vektoren von zwei GD
- Vorverarbeitung und räumliche Normalisierung
- Führen Sie die Korrektur der Wirbelstrom-induzierten geometrischen Verzerrungen der Echo-Planar-Imaging-Datensätzen nach der von 34 vorgeschlagen.
- Für den stereotaktischen Normalisierung, erstellen eine Studie-spezifischen (b = 0) - Vorlage und ein FA-Vorlage als zuvor 17,28,31 beschrieben. Grundsätzlich besteht eine vollständige nichtlineare stereotaktischen Normalisierung der drei Komponenten Verformung. Folglich ist die resultierende Diffusionstensors
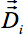 jedes Voxel i muss drehbar seined nach allen oben aufgeführten Umdrehungen (Fig. 4):
jedes Voxel i muss drehbar seined nach allen oben aufgeführten Umdrehungen (Fig. 4): - 4a zeigt eine starre Transformation Gehirn, um die Basis-Koordinatensystem Rahmen auszurichten. Die Drehung
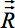 die sich aus der Ausrichtung auf das Basiskoordinatensystem Rahmen aufgebracht werden muss
die sich aus der Ausrichtung auf das Basiskoordinatensystem Rahmen aufgebracht werden muss 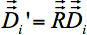
- 4b zeigt eine lineare Deformation nach Sehenswürdigkeiten. Die Komponenten der Eigenvektoren
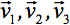 sind entsprechend den sechs Normalisierung Parameter s (abhängig von der Gehirnregion s a,, a = 1 ... 6) der linearen Verformung angepasst werden.
sind entsprechend den sechs Normalisierung Parameter s (abhängig von der Gehirnregion s a,, a = 1 ... 6) der linearen Verformung angepasst werden.
v w, j '' '= S ein v w, j'''
w = 1,2,3 und j = x, y, z. - 4c zeigt eine nichtlineare Normalisierung Ausgleich nichtlinearer Gehirn Form Unterschiede. Die 3D-Vektor Schichten sind für jeden Voxel, die zu einem separaten Transformation für jeden Voxel des 3D-Voxel Array
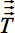 ). Norm Trigonometrie gibt eine Rotationsmatrix unabhängig für jedes Voxel, die sich aus dem 3-D Vektors verschiebt nach den Konzepten von 16, um die Beziehungen zwischen direktionalen Eigenvektoren neighbored Voxel zu bewahren. So führen verschiedene Schichten von zwei neighbored Voxel in Drehungen der entsprechenden Eigenvektoren. Verwenden Sie die Dilatation Matrizen für die Ausrichtung der Tensor
). Norm Trigonometrie gibt eine Rotationsmatrix unabhängig für jedes Voxel, die sich aus dem 3-D Vektors verschiebt nach den Konzepten von 16, um die Beziehungen zwischen direktionalen Eigenvektoren neighbored Voxel zu bewahren. So führen verschiedene Schichten von zwei neighbored Voxel in Drehungen der entsprechenden Eigenvektoren. Verwenden Sie die Dilatation Matrizen für die Ausrichtung der Tensor 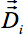 jedes Voxeldie umliegenden Voxel.
jedes Voxeldie umliegenden Voxel. 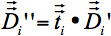
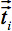 sind die Komponenten
sind die Komponenten 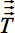
- 4a zeigt eine starre Transformation Gehirn, um die Basis-Koordinatensystem Rahmen auszurichten. Die Drehung
- Nach dieser Normalisierung einzelnen Verfahren (step (i) - DTI-Daten I 0), verwenden alle individuellen DTI-Datensätze für die Erstellung einer Studie-spezifischen (b = 0) - Vorlage und ein FA-Vorlage (Schritt (ii) - Vorlagen T 1). Als nicht-affine Registrierung zu einem FA-Vorlage hat den Vorteil, dass es mehr Kontrast bietet im Vergleich zu (b = 0) 10 Bilder, definieren Sie eine FA-Vorlage durch Mittelung alle einzeln abgeleitet FA-Karten der Patienten und die Kontrollen.
- In einem zweiten Schritt, nach den Grundideen der Ashburner und Friston 35, führen Sie eine nicht-lineare MNI Normalisierung (Schritt (iii)) der DTI-Datensätze durch Minimierung der Diskrepanz zwischen regionalen Intensitäten des FA-Karte ausgestattet sein und von der FA-Vorlage nach der quadrierten Differenzen (X 2) - auf diese Weise erhalten Sie DTI Daten I 1.
- Basierend auf diesen Daten werden neue Vorlagen T 2 abgeleitet (Schritt (iv)). Wiederholen Sie diesen iterativen Prozess, bis die Korrelation zwischen den einzelnen FA-Karten und ter FA-Vorlage ist> 0,7. Normalerweise ist dies nach zwei Iterationen erreicht.
- Whole-Brain-basierten räumlichen Statistik
Die folgenden Schritte 1.3.1 bis 1.3.5 werden visualisiert schematisch in Abbildung 5b.- Berechnen FA-Karten aus normalisierten DTI-Daten in Bezug auf die Normalisierung der Verfahren 1.2. um Richtungsinformation (Schritt (i)) zu erhalten.
- Als Vorverarbeitung Schritt vor voxelwise statistischen Vergleich, gelten ein Glättungsfilters (Schritt (ii)) zu den einzelnen normierten FA-Karten. Für Glättung, erfordert die Tatsache, dass der Filter Größe die Ergebnisse der Datenanalyse DTI 36 beeinflusst Anwendung der angepassten Filter Satz, dass die Breite des verwendeten Filters, um die Daten zu verarbeiten, um die Größe des erwarteten Unterschied sollte angepasst werden, erklärt, wie detaillierte in früheren Anwendungen DTI Daten von Patienten mit neurodegenerativen Erkrankungen (z. B. 28).
- Führen Sie statistische Layoutarison zwischen den Patientengruppen und der entsprechenden Kontrollgruppe voxelwise durch den Student-t-Test, dh vergleichen FA-Werte der Patienten FA-Karten mit den FA-Werte der Kontrollen 'FA-Karten, für jedes Voxel getrennt (Schritt (iii )). FA-Werte unter 0,2 sind für die Berechnung nicht berücksichtigt, da kortikalen grauen Substanz zeigt FA-Werte bis zu 0,2 37.
- Statistische Ergebnisse müssen für multiple Vergleiche mit der falsch-Entdeckung-Rate (FDR)-Algorithmus bei p <0,05 38 (Schritt (iv)) korrigiert werden. Weitere Reduktion der alpha Fehler muss durch eine räumliche Korrelationsalgorithmus (Clustering - Schritt (v)) durchgeführt werden, die getrennt Voxel oder kleine isolierte Gruppen von Voxel im Größenbereich der Glättung Kernel beseitigt, was zu einer Schwelle von 512 Cluster-Größe Voxel.
- Um die Ergebnisse auf einer morphologischen Hintergrund (Schritt (v)) anzuzeigen, normalisieren die 3-D-T1-gewichtete Datensätze zu MNI Raum und durchschnittlich arithmetisch. Führen Sie diese Normalisierung pERFAHREN durch Verwendung einer Template-Studie in Analogie zur Normalisierung, die auf die DTI Datensätze 17.
Abbildung 6 zeigt die Ergebnisse der ganze Gehirn-basierten räumlichen Statistik (WBSS) von ALS-Patienten vs Kontrollen. 6a zeigt das lokale Maximum der verringerten FA-Werte in einem sagittal, coronar und axiale Ansicht (bei p <0,01 Schwellenwert, korrigiert für multiple Vergleiche). 6b zeigt Projektionsdensitometriesystem FT mit Ausgangspunkten in der corticospinalen Traktes als Basis für TFAS verwendet. 6c zeigt Unterschiede zwischen den Gruppen in FA-Karten ganze Gehirn basiert räumlichen Statistik (WBSS) zwischen einer Probe von ALS-Patienten und Kontrollpersonen in erkannt a slicewise Visualisierung.
- Traktographie und tractwise fraktionierte Anisotropie Statistik (TFAS)
Abbildung 7 zeigt den Prozess der Gruppen-basierte FT einschließlich TFAS wie in 1 beschrieben.4.1 bis 1.4.4.- Um Gruppen-basierte FT Algorithmen anwenden, erzeugen gemittelt DTI Datensätze aus der Patienten-Daten und von den Kontrollen die Daten zusammen nach den zuvor beschriebenen Verfahren 17. Diese Mittelung erfordert eine sorgfältige Behandlung der Informationen, die die Orientierung im Prozess der Normalisierung nach Techniken, die von 16 beschrieben wird beibehalten - für Details 30 zu sehen.
- Führen tractography in gemittelten DTI Datensätze Fächergruppen durch Anwendung eines straffen Tracking-Technik 31. Identifizieren Sie manuell definiert Saatpunkte neben dem lokalen Maxima durch die gesamte Gehirn-basierte Analysen FA, die die Grundlage für die darauf folgenden FT-Analyse sind. Nach der Identifizierung der Samen, führen tractography und definieren die Voxel der abgegrenzt Fasern als gruppenspezifische Maske für die folgenden 30 TFAS.
- Um die Ergebnisse zu quantifizieren tractography gelten die Technik der TFAS mit the Nervenbahnen, die auf dem gemittelten DTI-Daten erstellt wurden Sätze von allen Probanden der einzelnen Gruppen (Patienten-und Steuerdaten zusammen) für die Auswahl der Voxel, die zu einem Vergleich zwischen den Patienten und der Kontrollen durch FA-Karten beitragen.
- Berücksichtigen Sie alle resultierenden Voxel mit einem FA-Wert oberhalb von 0,2 für die statistische Analyse durch den Student-t-Test.
- Falls gewünscht, könnte die TFAS Technik bei abgeleiteten DTI Metriken wie Mittelwert Diffusionsvermögen (MD), radiale Anisotropie, axial Anisotropie, usw. (Beispiel siehe 28) aufgebracht werden.
- Die Ergebnisse werden auf einer morphologischen Hintergrund aus den MNI normalisierte 3-D-T1-gewichtete Datensätze angezeigt
Access restricted. Please log in or start a trial to view this content.
Ergebnisse
1. QC und Korrektur für beschädigte Gradientenrichtungen in Anwendung, um Daten von Patienten mit hyperkinetischen Störungen
Als ein Beispiel für die Wirkung der Anwendung von QC und anschließende Volumen Ausgrenzung (als Konsequenz aus der Korrektur für beschädigte GD) Abbildung 8 zeigt Unterschiede in ganze Gehirn basierte räumliche Statistik mit und ohne Volumen Ausschluss für Group-Vergleich von 29 premanifest Huntington-Krankheit Themen vs 30 Alter und Geschlecht ...
Access restricted. Please log in or start a trial to view this content.
Diskussion
Die interindividuelle Mittelung DTI Daten können in Bezug auf Diffusion Amplitude (unter Verwendung von FA Information) und Diffusions-Richtung (basierend auf FT) erreicht sind. Mittelung von FA Karten ermöglicht die statistische Vergleich der Fächergruppen durch WBSS und TFAS. Diese methodischen Rahmen gibt eine Einführung in Techniken DTI mit inter-subject Mittelung und Group-Vergleich. Stereotaktischen Normalisierung und Vergleich von FA Karten auf Gruppenebene ermöglicht mehrere Möglichkeiten, um Unterschiede ...
Access restricted. Please log in or start a trial to view this content.
Offenlegungen
Autoren haben nichts zu offenbaren.
Danksagungen
Teile dieser Arbeit, das heißt die Studie über QC und Korrektur für beschädigte Gradientenrichtungen in Anwendung, um Daten von Patienten mit hyperkinetischen Störungen, wurden von der Europäischen HD Netzwerk (EHDN Projekt 070) unterstützt. Die MRT-Aufnahmen in dieser bestimmten Studie wurden als Teil der London-Website TRACK-HD Kohorte erworben.
Access restricted. Please log in or start a trial to view this content.
Materialien
| Name | Company | Catalog Number | Comments |
| MR scanner | Siemens 1.5 T Magnetom Symphony | ||
| analysis software | TIFT - Tensor Imaging and Fiber Tracking |
Referenzen
- Moseley, M. E., Cohen, Y., et al. Diffusion-weighted MR imaging of anisotropic water diffusion in cat central nervous system. Radiology. 176, 439-445 (1990).
- Mori, S., van Zijl, P. C. M. Fiber tracking: principles and strategies - a technical review. NMR Biomed. 15, 468-480 (2002).
- Basser, P. J., Mattiello, J., LeBihan, D. MR Diffusion Tensor Spectroscopy and Imaging. Biophys J. 66, 259-267 (1994).
- Mattiello, J., Basser, J. P., Le Bihan, D. Analytical expression for the b-matrix in NMR diffusion imaging and spectroscopy. J. Magn. Reson. A. 108, 131-141 (1994).
- Pierpaoli, C., Basser, P. J. Toward a quantitative assessment of diffusion anisotropy. Magn. Reson. Med. 36, 893-906 (1996).
- Pajevic, S., Pierpaoli, C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: application to white matter fiber tract mapping in the human brain. Magn. Reson. Med. 42, 526-540 (1999).
- Le Bihan, D., Mangin, J. F., et al. Diffusion tensor imaging: concepts and applications. J. Magn. Reson. Imaging. 13, 534-546 (2001).
- Conturo, T. E., Lori, N. F., et al. Tracking neuronal fibre pathways in the living human brain. Proc. Natl. Acad. Sci. U.S.A. 96, 10422-10427 (1999).
- Lori, N. F., Akbudak, E. Diffusion tensor fibre tracking of human brain connectivity: aquisition methods, reliability analysis and biological results. NMR Biomed. 15, 494-515 (2002).
- Smith, S. M., Jenkinson, M., et al. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 31, 1487-1505 (2006).
- Agosta, F., Pagani, E., et al. Assessment of white matter tract damage in patients with amyotrophic lateral sclerosis: a diffusion tensor MR imaging tractography study. AJNR. Am. J. Neuroradiol. 31, 1457-1461 (2010).
- Talairach, J., Tournoux, P. Coplanar stereotaxic atlas of the human brain. , Thieme Medical. New York. (1988).
- Brett, M., Johnsrude, I. S., Owen, A. M. The problem of functional localization in the human brain. Nat. Rev. Neurosci. 3, 243-249 (2002).
- Collins, D. L., Neelin, P., Peters, T. M., Evans, A. C. Automatic 3-D intersubject registration of MR volumetric data in standardized Talairach space. J. Comput. Assist. Tomogr. 18, 192-205 (1994).
- Friston, K. J., Ashburner, J., Frith, C. D., Poline, J. -B., Heather, J. D., Frackowiak, R. S. J. Spatial registration and normalization of images. Human Brain Mapp. 2, 165-189 (1995).
- Alexander, D. C., Pierpaoli, C., Basser, P. J., Gee, J. C. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans. Med. Imaging. 20, 1131-1139 (2001).
- Müller, H. -P., Unrath, A., Ludolph, A. C., Kassubek, J. Preservation of Diffusion Tensor Properties during Spatial Normalization by use of Tensor imaging and Fiber Tracking on a Normal Brain Database. Phys. Med. Biol. 52, N99-N109 (2007).
- Likitjaroen, Y., Meindl, T., et al. Longitudinal changes of fractional anisotropy in Alzheimer's disease patients treated with galantamine: a 12-month randomized, placebo-controlled, double-blinded study. Eur. Arch. Psychiatry Clin. Neurosci. 262, 341-350 (2012).
- Zhang, Y., Schuff, N. Progression of white matter degeneration in amyotrophic lateral sclerosis: A diffusion tensor imaging study. Amyotroph. Lateral Scler. 12, 421-429 (2011).
- Pierpaoli, C., Barnett, A. Water diffusion changes in Wallerian degeneration and their dependence on white matter architecture. Neuroimage. 13, 1174-1185 (2001).
- Agosta, F., Valsasina, P., et al. Sensorimotor functional connectivity changes in amyotrophic lateral sclerosis. Cereb Cortex. 21, 2291-2298 (2011).
- Müller, H. -P., Unrath, A., Huppertz, H. J., Ludolph, A. C., Kassubek, J. Neuroanatomical patterns of cerebral white matter involvement in different motor neuron diseases as studied by diffusion tensor imaging analysis. Amyotroph Lateral Scler. 13, 254-264 (2012).
- Reich, D. S., Zackowski, K. M. Corticospinal tract abnormalities are associated with weakness in multiple sclerosis. Am. J. Neuroradiol. 29, 333-339 (2008).
- Abe, O., Yamada, H. Amyotrophic lateral sclerosis: Diffusion tensor tractography and voxel-based analysis. NMR Biomed. 17, 411-416 (2004).
- Sage, C. A., Peeters, R. R., Gorner, A., Robberecht, W., Sunaert, S. Quantitative diffusion tensor imaging in amyotrophic lateral sclerosis. Neuroimage. 34, 486-499 (2007).
- Preti, M. G., Baglio, F., et al. Assessing corpus callosum changes in Alzheimer's disease: comparison between tract-based spatial statistics and atlas-based tractography. PLoS One. 7, e35856(2012).
- Borroni, B., Brambati, S. M., et al. Evidence of white matter changes on diffusion tensor imaging in frontotemporal dementia. Arch. Neurol. 64, 246-251 (2007).
- Unrath, A., Müller, H. -P., Riecker, A., Ludolph, A. C., Sperfeld, A. D., Kassubek, J. Whole brain-based analysis of regional white matter tract alterations in rare motor neuron diseases by diffusion tensor imaging. Hum Brain Mapp. 31, 1727-1740 (2010).
- Müller, H. -P., Lulé, D., Unrath, A., Ludolph, A. C., Riecker, A., Kassubek, J. Complementary Image Analysis of Diffusion Tensor Imaging and 3-Dimensional T1-Weighted Imaging: White Matter Analysis in Amyotrophic Lateral Sclerosis. J. Neuroimaging. 21, 24-33 (2011).
- Müller, H. -P., Unrath, A., Sperfeld, A. D., Ludolph, A. C., Riecker, A., Kassubek, J. Diffusion tensor imaging and tractwise fractional anisotropy statistics: quantitative analysis in white matter pathology. Biomed. Eng. Online. 6, 42(2007).
- Müller, H. -P., Unrath, A., Riecker, A., Pinkhardt, E. H., Ludolph, A. C., Kassubek, J. Inter-subject variability in the analysis of diffusion tensor imaging at the group level: fractional anisotropy mapping and fiber tracking techniques. Magn. Reson. Imaging. 27, 324-334 (2009).
- Müller, H. -P., Glauche, V., et al. Stability of white matter changes related to Huntington's disease in the presence of imaging noise: a DTI study. PLoS Curr. 3, RRN1232(2011).
- Müller, H. -P., Süßmuth, S. D., Landwehrmeyer, G. B., Ludolph, A. C., Tabrizi, S. J., Klöppel, S., Kassubek, J. Stability effects on results of diffusion tensor imaging analysis by reduction of the number of gradient directions due to motion artifacts: an application to presymptomatic Huntington's disease. PLoS Curr. 3, RRN1292(2011).
- Shen, Y., Larkman, D. J., Counsell, S., Pu, I. M., Edwards, D., Hajnal, J. V. Correction of High-Order Eddy Current Induced Geometric Distortion in Diffusion-Weighted Echo-Planar images. Magn. Reson. Med. 52, 1184-1189 (2004).
- Ashburner, J., Friston, K. J. Nonlinear Spatial Normalization Using Basis Functions. Human Brain Mapping. 7, 254-266 (1999).
- Jones, D. K., Symms, M. R., Cercignani, M., Howard, R. J. The effect of filter size on VBM analyses of DT-MRI data. Neuroimage. 26, 546-554 (2005).
- Kunimatsu, A., Aoki, S., et al. The optimal trackability threshold of fractional anisotropy for diffusion tensor tractography of the corticospinal tract. Magn. Reson. Med. Sci. 3, 11-17 (2004).
- Genovese, C. R., Lazar, N. A., Nichols, T. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage. 15, 870-878 (2002).
- Cleaver, J. E. Defective repair replication of DNA in xeroderma pigmentosum. Nature. 218, 652-656 (1968).
- Anttinen, A., Koulu, L., et al. Neurological symptoms and natural course of xeroderma pigmentosum. Brain. 131, 1979-1989 (2008).
- Kassubek, J., Sperfeld, A. D. The cerebro-morphological fingerprint of a progeroid syndrome: white matter changes correlate with neurological symptoms in xeroderma pigmentosum. PLoS One. 7, e30926(2012).
- Canu, E., Agosta, F. The topography of brain microstructural damage in amyotrophic lateral sclerosis assessed using diffusion tensor MR imaging. AJNR. Am. J. Neuroradiol. 32, 1307-1314 (2011).
- Verstraete, E., Veldink, J. H., Hendrikse, J., Schelhaas, H. J., van den Heuvel, M. P., van den Berg, L. H. Structural MRI reveals cortical thinning in amyotrophic lateral sclerosis. J. Neurol. Neurosurg. Psychiatry. 83, 383-388 (2012).
- Hofer, S., Frahm, J. Topography of the human corpus callosum revisited- comprehensive fiber tractography using diffusion tensor magnetic resonance imaging. Neuroimage. 32, 989-994 (2006).
- Iwata, N. K., Kwan, J. Y., et al. White matter alterations differ in primary lateral sclerosis and amyotrophic lateral sclerosis. Brain. 134, 2642-2655 (2011).
- Kassubek, J., Ludolph, A. C., Müller, H. -P. Neuroimaging of motor neuron diseases. Ther. Adv. Neurol. Disord. 5, 119-127 (2012).
- Kassubek, J., Juengling, F. D. Multimodality functional neuroimaging. In: C. Stippich (Ed.): Clinical functional MRI - Presurgical functional neuroimaging. , Springer. Berlin/Heidelberg/New York. (2007).
- Stadlbauer, A., Buchfelder, M., Salomonowitz, E., Ganslandt, O. Fiber density mapping of gliomas: histopathologic evaluation of a diffusion-tensor imaging data processing method. Radiology. , 257-846 (2010).
- Stadlbauer, A., Hammen, T., et al. Differences in metabolism of fiber tract alterations in gliomas: a combined fiber density mapping and magnetic resonance spectroscopic imaging study. Neurosurgery. 71, 454-463 (2012).
- Staempfli, P., Jaermann, T., Crelier, G. R., Kollias, S., Valavanis, A., Boesiger, P. Resolving fiber crossing using advanced fast marching tractography based on diffusion tensor imaging. Neuroimage. 30, 110-120 (2006).
- Ehricke, H. H., Otto, K. M., Klose, U. Regularization of bending and crossing white matter fibers in MRI Q-ball fields Magn. Reson Imaging. 29, 916-926 (2011).
- Hirsch, J. G., Schwenk, S. M., Rossmanith, C., Hennerici, M. G., Gass, A. Deviations from the diffusion tensor model as revealed by contour plot visualization using high angular resolution diffusion-weighted imaging (HARDI). MAGMA. 16, 93-102 (2003).
- Lazar, M., Weinstein, D. M., et al. White matter tractography using diffusion tensor deflection. Human Brain Mapping. 18, 306-321 (2003).
- Reisert, M., Mader, I., Anastasopoulos, C., Weigel, M., Schnell, S., Kiselev, V. Global fiber reconstruction becomes practical. Neuroimage. 54, 955-962 (2011).
- Klein, A., Andersson, J. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage. 46, 786-802 (2009).
- Bammer, R. Basic principles of diffusion-weighted imaging. Eur. J. Radiol. 45, 169-184 (2003).
- Mohammadi, S., Keller, S. S. The influence of spatial registration on detection of cerebral asymmetries using voxel-based statistics of fractional anisotropy images and TBSS. PLoS One. 7, e36851(2012).
- Turner, M. R., Grosskreutz,, et al. Towards a neuroimaging biomarker for amyotrophic lateral sclerosis. Lancet Neurol. 10, 400-403 (2011).
- Müller, H. -P., Kassubek, J. Multimodal imaging in neurology - special focus on MRI applications and MEG. Synthesis Lectures in Biomedical Engineering. Enderle, J. D. 16, Morgan & Claypool Publishers. (2008).
- Douaud, G., Filippini, N., Knight, S., Talbot, K., Turner, M. R. Integration of structural and functional magnetic resonance imaging in amyotrophic lateral sclerosis. Brain. 134, 3470-3479 (2011).
- Kolind, S. H., Laule, C., et al. Complementary information from multi-exponential T2 relaxation and diffusion tensor imaging reveals differences between multiple sclerosis lesions. Neuroimage. 40, 77-85 (2008).
- Verma, R., Zacharaki, E. I. Multiparametric tissue characterization of brain neoplasms and their recurrence using pattern classification of MR images. Acad. Radiol. 15, 966-977 (2008).
Access restricted. Please log in or start a trial to view this content.
Nachdrucke und Genehmigungen
Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden
Genehmigung beantragenWeitere Artikel entdecken
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten