Se requiere una suscripción a JoVE para ver este contenido. Inicie sesión o comience su prueba gratuita.
Method Article
Que forma la amplitud y fase de rayos láser mediante el uso de un modulador de luz espacial sólo fase
En este artículo
Resumen
Mostramos cómo codificar el complejo campo de rayos láser mediante el uso de un elemento monofásico. Un interferómetro de sendero común se emplea para mezclar la información de fase mostrada en un modulador de luz espacial fase sólo para finalmente recuperar el patrón de campo complejo deseado en la salida de un sistema de proyección de imagen óptica.
Resumen
El objetivo de este artículo es demostrar visualmente la utilización de un método de interferometría para la codificación de campos complejos asociados con la radiación de láser coherente. El método se basa en la suma coherente de dos ondas uniforme, previamente codificadas en un solo fase espacial luz modulador (MST) por multiplexación espacial de sus fases. Aquí, el proceso de interferencia se lleva a cabo por filtración espacial de frecuencias de luz en el plano de Fourier de determinado sistema de proyección de imagen. La correcta aplicación de este método permite fase arbitraria y amplitud información a ser recuperada en la salida del sistema óptico.
Es una técnica de codificación sobre el eje, en lugar de fuera del eje, con un algoritmo de procesamiento directo (no un bucle iterativo) y libre de ruido coherente (moteado). El campo complejo puede ser obtenido exactamente a la salida del sistema óptico, excepto algo de pérdida de resolución debido al proceso de filtrado de frecuencia. La principal limitación del método podría provenir de la incapacidad de operar con tasas de frecuencia más altas que la tasa de refresco de la SLM. Usos incluyen, pero no se limitan a, microscopia lineal y no lineal, que forma el rayo o láser micro-tratamiento de superficies.
Introducción
Casi todas las aplicaciones de láser están en estrecha relación con la gestión de lo frente de onda óptico de la luz. En la aproximación paraxial, el campo complejo asociado con la radiación láser se puede describir por dos términos, la amplitud y la fase. Tener control sobre estos dos términos es necesario modificar tanto la temporal y la estructura espacial de rayos láser en la voluntad. En general, la amplitud y la fase de un rayo láser pueden correctamente cambiar por varios métodos incluyendo el uso de componentes ópticos que van de a granel solo lentes, divisores de viga y espejos para dispositivos más complejos como espejos deformables o luz espacial moduladores. A continuación, os mostramos un método de codificación y reconstruir el complejo campo de rayos de láser coherente, que se basa en la teoría de holograma doble fase1y la utilización de un interferómetro de camino común.
Hoy en día, existe una gran variedad de métodos para codificar los campos complejos de laser vigas2,3,4,5. En este contexto, algunos métodos bien establecidos de fase y modulación de amplitud se basan en el uso de hologramas digitales6. Un punto común en todos estos métodos es la necesidad de generar un desplazamiento espacial para separar el haz de salida deseada de la zeroth-orden procedente de la reflexión de la luz en la pantalla SLM. Estos métodos son básicamente fuera de eje (generalmente aplicando para el primer orden de difracción de la rejilla), con rejilla de fase no sólo para codificar la fase, sino también introducir la necesaria modulación de amplitud. En particular, modulación de amplitud se realiza bajando espacialmente a la altura de la reja, que claramente se degrada la eficiencia de difracción. El proceso de reconstrucción de holograma sobre todo obtiene una reconstrucción aproximada pero no exacta, de la amplitud y la fase del campo complejo deseado. Las discrepancias entre teoría y experimento parecen que aparecen a partir de una codificación incorrecta de la información de amplitud, así como otras cuestiones experimentales ocurre durante el filtrado espacial de primer orden de difracción o debido a los efectos de pixelado SLM. Además, el perfil de intensidad de la viga de entrada puede introducir restricciones en la potencia de salida.
En cambio, con el método introducido7, toda la gestión de luz se realiza sobre el eje, que es muy conveniente desde el punto de vista experimental. Además, se aprovecha de considerar, en la aproximación paraxial, el complejo campo asociado con los rayos laser como la suma de dos ondas uniforme. La información de amplitud es sintetizado por la interferencia de las ondas uniforme. En la práctica, dicha interferencia se lleva a cabo por filtración espacial de frecuencias de luz en el plano de Fourier de un determinado sistema de proyección de imagen. Anteriormente, los patrones de fase asociados a ondas uniformes son multiplexados espacial y codificados en una solo fase SLM (colocado en el plano de entrada de este sistema de proyección de imagen). Por lo tanto, la configuración del conjunto óptica puede considerarse como un interferómetro de camino común (muy robusto contra vibraciones mecánicas, cambios de temperatura o desalineación óptica). Por favor, tenga en cuenta que el proceso de interferencia antes mencionadas se puede lograr también utilizando otros diseños ópticos: con un par de SLMs fase sólo bien colocado dentro de un interferómetro de dos brazos típico, o por tiempo de codificación de forma secuencial las dos fases patrones en el SLM (previa introducción de un espejo de referencia en la configuración óptica). En ambos casos, no hay ninguna necesidad de filtrado espacial y por lo tanto sin pérdida de resolución espacial, a expensas de aumentar la complejidad del sistema óptico, así como el proceso de alineación. Aquí, cabe también destacar que mediante el uso de este método de codificación, el espectro completo del campo complejo deseado puede ser obtenido exactamente en el plano de Fourier, después de filtrar todas las órdenes de difracción, pero el cero uno.
Por otro lado, la eficiencia del método depende de varios factores: las especificaciones del fabricante de SLM (p. ej., fill factor, reflexión o difracción de eficiencia), el tamaño del patrón codificado y la manera en que la luz incide sobre la SLM (reflexión con un pequeño ángulo de bateo o incidencia normal mediante el uso de un divisor de haz). En este punto, bajo condiciones experimentales apropiadas, el rendimiento medido de luz total puede ser más del 30%. Sin embargo, tenga en cuenta que el rendimiento total de la luz sólo debido al uso del SLM que puede menos del 50%. La falta de al azar o elementos del difusor dentro de la óptica configuración permite la recuperación de los patrones de amplitud y fase sin ruido coherente (moteado). Otros aspectos importantes a señalar son la utilización de un algoritmo de codificación directa en lugar de procedimientos iterativos y su capacidad para realizar arbitraria e independiente de la amplitud y modulación de la fase en la frecuencia actualización (hasta tiempo del SLM cientos de hertz según la tecnología actual).
En principio, el método7 está diseñado para ser utilizado con ondas planas de entrada, pero no se limita a eso. Por ejemplo, si un haz gaussiano es golpear el MST, es posible modificar su forma de irradiación en la salida del sistema mediante la codificación de un patrón de amplitud adecuada en el SLM. Sin embargo, como la intensidad del haz de salida no puede excederla de la viga de entrada en cualquier posición transversal (x, y), la forma de la amplitud se realiza por las pérdidas de intensidad originadas por un proceso de interferencia parcialmente destructiva.
La teoría subraya la codificación de método7 es como sigue. Cualquier campo complejo representado en la forma U(x,y)= A(x,y)eφ()x,y) también puede reescribirse como:
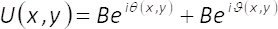 (1)
(1)
donde
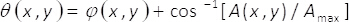 (2)
(2)
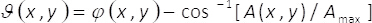 (3)
(3)
En las ecuaciones 1-3, la amplitud y la fase del complejo bidimensional del campo U(x,y)está dada por el A(x,y) y φ(x,y), respectivamente. Tenga en cuenta que términos unmáximo (máximo de A(x,y)) y B = unmáximo/2 no dependen de las coordenadas transversales (x,y). De la teoría, si establece unamáxima= 2, entonces B =1. Por lo tanto, el complejo campo U(x,y) puede obtenerse de una manera sencilla, desde la suma coherente de ondas uniforme serθ()x,y) y iθ (x,y). En la práctica, esto se logra con un interferómetro de camino común compuesto de una sola fase elemento α(x,y), en el plano de entrada de un sistema de proyección de imagen. El elemento monofásico es construido por multiplexación espacial de los términos de fase θ(x,y)
y θ (x,y) con la ayuda de dos dimensiones rejillas binarias (patrones de tablero de ajedrez) M1(x,y) y M2(x,y) como sigue
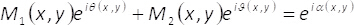 (4)
(4)
por lo tanto,
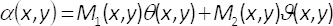 (5)
(5)
Estos patrones binarios cumplir con la condición de M1(x,y) + M2(x,y) = 1. Tenga en cuenta que, la interferencia de ondas uniforme no puede ocurrir si no mezclamos la información contenida en el elemento de faseα(x,y). En el presente método, esto se lleva a cabo mediante el uso de un filtro espacial capaz de bloquear todas las órdenes de difracción, pero el cero uno. De esta manera, tras el proceso de filtrado en el plano de Fourier, el espectro de H(u,v)= F{eiα()x,y)} de la fase codificada función está relacionada con el espectro del campo complejo F{U(x,y)} por la expresión
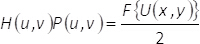 (6)
(6)
En la ecuación (6), (u,v) indican coordenadas en el dominio de la frecuencia, P(u,v) tiene el filtro espacial, mientras que la transformada de Fourier de una función dada Θ(x,y) se representa en forma F {Θ(x,y)}. De ecuación (6), se sigue que, en el plano de salida del sistema de proyección de imagen, el campo complejo obtenido URET(x,y), (sin considerar factores constantes), está dada por la convolución de la magnificada y espacial complejo campo U(x,y) la transformada de Fourier de la máscara de filtro invertido. Es decir:
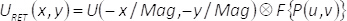 (7)
(7)
En la ecuación (7), la operación de convolución se denota por el símbolo  y el término Mag representa la ampliación del sistema de proyección de imagen. Por lo tanto, la amplitud y fase de U(x,y) es totalmente obtenido en el plano de salida, excepto una pérdida de resolución espacial debido a la operación de convolución.
y el término Mag representa la ampliación del sistema de proyección de imagen. Por lo tanto, la amplitud y fase de U(x,y) es totalmente obtenido en el plano de salida, excepto una pérdida de resolución espacial debido a la operación de convolución.
Access restricted. Please log in or start a trial to view this content.
Protocolo
1. codificar el complejo campo en un elemento monofásico
- De las especificaciones técnicas de la SLM, encontrar su resolución espacial (por ejemplo píxeles 1920 píxeles x 1800).
- Definir y generar la amplitud deseada A(x,y) y la fase φ(x,y) patrones como imágenes digitales.
- Conjunto de la resolución espacial del citado digitales imágenes igual a la de la pantalla SLM.
- Conjunto de imágenes digital mencionado en formato de nivel de gris.
- Ajustar los valores mínimos y máximos de las imágenes de fase y amplitud de 0 a 255 y de - π/2 π/2, respectivamente.
- Establecer unmáximo = 2 en las ecuaciones 2 y 3 y computadora-generar la fase patrones θ(x,y) y θ(x,y) de ellos.
- Computadoras generan los patrones de tablero M1(x,y) y M2(x,y).
- Establezca la resolución espacial de estos patrones de tablero de ajedrez en de la pantalla SLM.
- Para reducir el efecto de diafonía píxel, generar otros pares de patrones de tablero M1(x,y) y M2(x,y) construido con células diferentes píxeles que tienen un mayor número de píxeles (por ejemplo: células de pixel 2 x 2, 3 x 3 y 4 x 4, etc.).
PRECAUCIÓN: Al aumentar la celda píxel, el número total de píxeles de los patrones del tablero de ajedrez debe mantenerse invariable e igual a la resolución espacial de la SLM. Asegúrese de que el número final de píxeles de todos los patrones de tablero de ajedrez sigue siendo la misma después de modificar las celdas de píxeles.
- Computadora generar el elemento de una fase α(x,y) de la ecuación 5.
Nota: Ver material suplementario llamado "MATLAB_code_1.m" para las tareas relacionadas en el paso 1 de este protocolo.
2. reconstrucción del complejo campo de
- Utilizar un rayo láser colimado, linear polarizado y espacialmente coherente como una fuente de luz.
- Utilizar un SLM sólo fase con menos rango de fase de 2π.
- Cuando sea necesario, utilizar un expansor de haz adecuadas para ajustar el tamaño de la viga para el tamaño de la pantalla SLM.
- Cuando sea necesario, utilizar un polarizador óptico para establecer la polarización del haz de láser en la dirección horizontal. Esto es generalmente importante para el correcto funcionamiento de fase sólo SLMs, que están diseñados para modular la fase espacial del campo electromagnético que oscila en la dirección horizontal, manteniendo sin cambios sus componentes verticales.
- Para enviar un patrón de fase para el SLM, seguir protocolos de comunicación estándar de SLM fabricante para conectar y controlar el MST con la computadora.
Nota: Protocolo común para este propósito incluye el uso de una curva de calibración para transformar los valores en radianes (debido a las operaciones matemáticas con ángulos) en nivel gris, que la unidad de control electrónico de la SLM se convertirá finalmente en niveles de tensión. Además, el MST está conectado al ordenador como un dispositivo externo con pantalla propia, una extensión de la pantalla del ordenador es generalmente necesario, así como un programa adecuado para enviar las imágenes nivel gris correspondientes a esta pantalla extra. Un ejemplo de estos códigos también se incluye como material suplementario (véase MATLAB_code_2.m). - Implementar un sistema óptico de la imagen y poner la pantalla de lo SLM en el plano de entrada de este sistema.
- Utilizar una lente refractiva de una longitud focal f para construir un sistema de óptica de la imagen def 2f x 2 (un sistema óptico 4f también es válido para esta tarea). Según el tamaño de la salida prevista del campo complejo, ángulo, longitud de onda de la luz y el espacio físico disponible, emplear lentes/lentes con adecuadas especificaciones técnicas (por ejemplo, capa, tamaño, distancia focal, etc.).
- Para encontrar la posición del plano de salida del sistema de proyección de imagen, enviar el patrón de fase α(x,y) para el MST y busque visualmente la imagen grabada (dependiendo de la posición de la cámara) con la mejor resolución espacial.
PRECAUCIÓN: En el caso de bajo tamaño pixel células (por ejemplo, 1 x 1 píxeles) y muestra SLM con un ancho de píxel de unas pocas micras (por ejemplo, 8 μm), sólo haz de propagación puede producir interferencia entre ondas uniforme codificadas, consiguiendo una imagen reconstruida sin incluir el diafragma circular en el sistema de proyección de imagen. Utilizan células de bajo tamaño pixel para ubicar la posición del plano de salida. - Colocar un diafragma circular de diámetro variable en el plano de Fourier del sistema óptico y alinear su centro con la del foco del rayo láser.
- Para ajustar el tamaño del diafragma circular en el plano de Fourier, enviar el patrón de fase α(x,y) y buscar visualmente la imagen grabada (dependiendo del diámetro del diafragma circular) con mejor resolución espacial.
PRECAUCIÓN: En el caso de largo tamaño pixel células (por ejemplo, 4 x 4 píxeles), la interferencia entre ondas uniforme codificadas básicamente realiza con el filtro espacial. Utilice la celda de largo tamaño píxel para ajustar el tamaño del diafragma circular. En este protocolo, los términos bajo tamaño y tamaño de largo se refieren al número de píxeles contenidos en una celda de pixel. Sin embargo, la mencionada interferencia depende también de la anchura del pixel. Emplear SLMs con pixel ancho igual o inferior a 8 μm.
- Enviar la imagen gris de nivel correspondiente a la fase elemento α(x,y) para el MST.
- Para minimizar el efecto de diafonía, busque el mejor tamaño de celda de píxeles que permiten obtener la imagen grabada con la mayor resolución espacial.
3. Mida el campo complejo reconstruido
- Implementar la fase de polarización cambio técnica8.
- Coloque y alinee el ángulo de rotación del primer polarizador óptico, situado justo antes del SLM (ver figura 2). Para ajustar el ángulo de rotación del primer polarizador, busque visualmente la transmitencia ligera máxima y mínima en la cámara del CCD (colocada en el plano de salida del sistema de proyección de imagen), dependiendo de la rotación del polarizador. Anote los dos ángulos correspondientes del polarizador. Fijar el ángulo final del polarizador entre los dos ángulos anteriores registrados.
- Coloque y alinee el ángulo de rotación del segundo polarizador óptico, situado tras el plano de Fourier del sistema de proyección de imagen (ver figura 2). Para ajustar el ángulo de rotación del segundo polarizador, visualmente busque las imágenes más nítidas y más borrosas de la cámara CCD (colocado en el plano de salida del sistema de proyección de imagen) después de enviar el patrón de fase α(x,y) para el MST. Anote los dos ángulos correspondientes del polarizador. Fijar el ángulo final del segundo polarizador entre los ángulos anteriores registrados.
- Grabar los interferograms.
- Mantenga la cámara en el plano de salida del sistema de proyección de imagen.
- Para grabar la primera interferograma, añadir una matriz de 0 radianes al elemento de fase α(x,y) y enviarlo al SLM. Grabar imagen correspondiente I1(x,y) con el CCD.
- Para grabar el segundo interferograma, añadir una matriz de π/2 radianes al elemento de fase α(x,y) y enviarlo al SLM. Grabar imagen correspondiente 2(x,y) con la cámara CCD.
- Para grabar la tercera interferograma, añadir una matriz de radianes π para el elemento de fase α(x,y) y enviarlo al SLM. Grabar imagen correspondiente 3(x,y) con la cámara CCD.
- Para grabar el cuarto y último interferograma, añadir una matriz de 3π/2 radianes al elemento de fase α(x,y) y enviarlo al SLM. Grabar imagen correspondiente I4(x,y) con la cámara CCD.
- Reconstruir el campo complejo.
Nota: Ver material suplementario llamado "MATLAB_code_3.m" para las tareas relacionadas en este punto del protocolo.- Recuperar la amplitud del campo complejo unobtenido(x,y) mediante la expresión
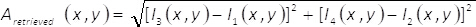 (8)
(8) - Recuperar la fase del campo complejo φobtenido(x,y) mediante la expresión
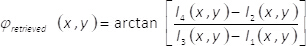 (9)
(9)
- Recuperar la amplitud del campo complejo unobtenido(x,y) mediante la expresión
Access restricted. Please log in or start a trial to view this content.
Resultados
La resolución espacial de la SLM sólo fase empleada es 1920 píxeles x 1080 píxeles, con una echada del pixel de 8 μm. La amplitud seleccionada A(x,y) y la fase φ(x,y) del campo complejo se definen por dos imágenes diferentes de nivel gris correspondiente a la imagen de Lenna conocido (patrón de amplitud) y una niña sobresale su lengua (patrón de fase), respectivamente. En general, para la generación de patrones necesarios ta...
Access restricted. Please log in or start a trial to view this content.
Discusión
En este protocolo, práctica parámetros como el ancho de píxel del SLM sólo fase o el número de píxeles contenidos dentro de las celdas de píxeles de un patrón generado por ordenador son puntos clave para implementar con éxito el método de codificación. En pasos 1.2, 1.3 y 1.4 del Protocolo, menor será el ancho de píxel, mejor será la resolución espacial de los patrones obtenidos de amplitud y fase. Además, como la codificación en el SLM de modulaciones de fase de pixel a pixel abruptas puede originar res...
Access restricted. Please log in or start a trial to view this content.
Divulgaciones
Los autores no tienen nada que revelar.
Agradecimientos
Esta investigación fue apoyada por la Generalitat Valenciana (PROMETEO 2016-079), Universitat Jaume I (UJI) (UJIB2016-19); y Ministerio de Economía y Competitividad (MINECO) (FIS2016-75618-R). Los autores están muy agradecidos al SCIC de la Universitat Jaume I para el uso del láser de femtosegundo.
Access restricted. Please log in or start a trial to view this content.
Materiales
| Name | Company | Catalog Number | Comments |
| Achromatic Doublet | THORLABS | AC254-100-B-ML | Lens Diameter 25.4 mm, focal length 100 mm |
| Achromatic Galilean Beam Expander | THORLABS | GBE05-A | AR Coated: 400 - 650 nm |
| Basler camera | BASLER | avA1600-50gm GigE camera | sensor size 8.8 mm x 6.6 mm, pizel size 5.5 microns |
| Mounted Zero-Aperture Iris | THORLABS | ID12Z/M | Max Aperture 12 mm |
| Pellicle Beamsplitter | THORLABS | CM1-BP145B2 | 45:55 (R:T), Coating: 700 - 900 nm |
| PLUTO Spatial Light Modulator | HOLOEYE Photonics AG | NIR-II | Phase Only Spatial Light Modulator (Optimized for 700 -1000 nm) |
| Two thin film laser polarizers | EKSMA OPTICS | 420-0526M | material BK7, diameter 50 mm, wavelength 780-820 nm |
Referencias
- Hsueh, C. K., Sawchuk, A. A. Computer-generated double-phase holograms. Applied Optics. 17 (24), 3874-3883 (1978).
- Arrizón, V. Complex modulation with a twisted-nematic liquid-crystal spatial light modulator: double-pixel approach. Optics Letters. 28 (15), 1359-1361 (2003).
- Arrizón, V., Ruiz, U., Carrada, R., González, L. A. Pixelated phase computer holograms for the accurate encoding of scalar complex fields. Journal of the Optical Society of America A. 24 (11), (2007).
- Shibukawa, A., Okamoto, A., Takabayashi, M., Tomita, A. Spatial cross modulation method using a random diffuser and phase-only spatial light modulator for constructing arbitrary complex fields. Optics Express. 22 (4), 3968-3982 (2014).
- Martínez-Fuentes, J. L., Moreno, I. Random technique to encode complex valued holograms with on axis reconstruction onto phase-only displays. Optics Express. 26 (5), 5875-5893 (2018).
- Clark, T. W., Offer, R. F., Franke-Arnold, S., Arnold, A. S., Radwell, N. Comparison of beam generation techniques using a phase only spatial light modulator. Optics Express. 24 (6), 6249-6264 (2016).
- Mendoza-Yero, O., Mínguez-Vega, G., Lancis, J. Encoding complex fields by using a phase-only optical element. Optics Letters. 39 (7), 1740-1743 (2014).
- Yamaguchi, I., Zhang, T. Phase-shifting digital holography. Optics Letters. 22 (16), 1268-1270 (1997).
- Shao, Y., et al. Addressable multiregional and multifocal multiphoton microscopy based on a spatial light modulator. Journal of Biomedical Optics. 17 (3), 030505(2012).
- Mendoza-Yero, O., Carbonell-Leal, M., Mínguez-Vega, G., Lancis, J. Generation of multifocal irradiance patterns by using complex Fresnel holograms. Optics Letters. 43 (5), 1167-1170 (2018).
- Kuang, Z., et al. Diffractive Multi-beam Ultra-fast Laser Micro-processing Using a Spatial Light Modulator (Invited Paper). Chinese Journal of Lasers. 36 (12), 3093-3115 (2009).
- Kuang, Z., et al. High throughput diffractive multi-beam femtosecond laser processing using a spatial light modulator. Applied Surface Science. 255, 2284-2289 (2008).
Access restricted. Please log in or start a trial to view this content.
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoThis article has been published
Video Coming Soon
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados