このコンテンツを視聴するには、JoVE 購読が必要です。 サインイン又は無料トライアルを申し込む。
Method Article
位相空間光変調を用いた振幅とレーザー光の位相を形成
要約
単相要素を使用してレーザー光の複雑なフィールドをエンコードする方法を示します。位相空間光変調光イメージング システムの出力で目的の複雑なフィールド パターンを最終的に取得するに表示される位相情報をミックスにコモンパス干渉計を採用します。
要約
この記事の目的は、視覚的にコヒーレント レーザー放射に関連付けられた複雑なフィールドをエンコードするため干渉法の使用率を示すことです。このメソッドは、以前の段階の空間多重化により、位相空間光変調器 (SLM) にエンコードされた 2 つの均一な波のコヒーレント和に基づいています。ここでは、干渉プロセスは、特定のイメージング システムのフーリエ平面上における光周波数の空間フィルタ リングによって実行されます。このメソッドの適切な実装では、任意の位相および振幅情報光学系の出力で取得することができます。
直接処理アルゴリズム (ない反復ループ)、軸外ではなく、軸上、エンコード技術で、コヒーレント ノイズ (スペックル) から無料します。複雑なフィールドは、周波数フィルター処理による解像度のいくつかの損失を除いて、光学系の出力で正確に取得をすることができます。このメソッドの主な制限は、SLM のリフレッシュ レートよりも高い頻度で動作することができないことから来るかもしれない。アプリケーションなどが、線形と非線型の顕微鏡やビーム成形、材料表面のレーザ マイクロ加工に限定されていません。
概要
レーザーのほとんどすべてのアプリケーションは、光の光の波面の管理と密接な関係です。近軸近似における 2 つの用語、振幅および位相によってレーザー放射に関連付けられている複雑なフィールドを記述できます。これらの 2 つの条件を制御することは、時間およびレーザー ビームの空間構造を変更する必要が。一般に、振幅とレーザー光の位相正しく変更できます光学部品の使用を含むいくつかの方法でその範囲一括レンズやビームスプリッター ミラーから変形ミラーまたは空間光変調器のような複雑なデバイスに変調器。ここでは、エンコードとデュアル位相ホログラム理論1に基づくコヒーレント レーザ光線の複雑なフィールドとコモンパス干渉計の利用を再構築するための手法を示す.
今日では、さまざまなレーザー ビーム2,3,4、5の複雑なフィールドをエンコードするためのメソッドが存在します。ここで、位相と振幅変調を生成するいくつかのよく確立された方法はデジタル ホログラム6の使用に依存します。これらすべてのメソッドの共通点は、空間オフセットを生成する SLM ディスプレイの光の反射から来る zeroth 順序から所望の出力ビームを分離する必要性です。これらのメソッドは基本的にオフ軸 (通常は格子の最初の回折次数の適用)、位相格子だけでなく、位相をエンコードするだけでなく必要な振幅変調を導入するを採用します。特に、振幅変調は空間的回折効率が明らかに低下する回折格子の高さを下げることによって実行されます。ホログラム、再建のプロセスはほとんどの振幅・位相目的の複雑なフィールドに過ぎず、しかし、正確ではなく復興を取得します。理論と実験間の不一致は、最初の回折次数や SLM 戸惑い効果による空間フィルタ リングの間に起こってその他の実験的問題と同様に、振幅情報の不正確なエンコーディングから表示されるましょう。さらに、入射ビームの強度プロファイルは、出力電力の制限を導入できます。
対照的に、導入法7、すべて光管理を行う軸上実験の観点から非常に便利です。また、それは 2 つの均一な波の和としてレーザービームに関連付けられている複雑なフィールドを考えると、近軸近似の活用です。振幅情報はこれらの均一な波の干渉による synthetized です。実際には、このような干渉イメージング システムのフーリエ平面上における光周波数の空間フィルタ リングによって実行されます。以前は、統一の波に関連付けられている位相パターンは多重空間し、位相限定 SLM (このイメージング システムの入口面に配置) にエンコードします。したがって、光学構成全体のセットアップは、コモンパス干渉計 (機械振動、温度変化、または光のズレに対して非常に堅牢な) としてみなすことができます。なお、上記の干渉過程をまた他の光学レイアウトを使用して実現できます: 典型的な 2 アームの干渉計や順番にエンコード時間を正しく配置フェーズ専用 SLMs のカップルと 2 つの相パターン化して SLM (参照ミラー光のセットアップで以前紹介)。どちらの場合も、空間フィルタ リングの必要性とその結果配置プロセスと同様に光学系の複雑さを増加と引き換えに、空間分解能を損なうことがなくはありません。ここでは、このエンコード方式を使用して、目的の複雑なフィールドの完全なスペクトルことができるフーリエ平面に正確に取得をすべての回折の注文が 0 番目のものをフィルター処理した後はまた強調されるべき。
その一方で、メソッドの効率は、いくつかの要因に依存: SLM (例えば、フィル率、反射率、または回折効率) は、エンコードされたパターンと上に入射する光を方法のサイズの製造元の仕様、SLM (小さい打撃角度またはビームスプリッターを用いた垂直入射と反射)。この時点で、適切な実験条件下で測定の総光効率は 30% 以上をすることができます。ただし、SLM の使用のためにだけ総光効率が 50% 未満のものをすることができます。ランダムの欠如または光内のディフューザー要素セットアップは、コヒーレント ノイズ (スペックル) なしの振幅と位相のパターンを取得することができます。反復的なプロシージャと恣意的で独立した振幅および位相変調周波数で実行する能力は、最大 SLM の時間を更新ではなく、他の重要な側面を指摘するが直接符号化アルゴリズムの利用現在の技術によるとヘルツの数百人)。
原則として、方法7入力平面波で使用するものですに限定されるわけで。例えば、ガウスビームは、SLM に当たって場合、SLM に適しています振幅パターンをエンコードすることによってシステムの出力で照射形状を変更することが可能です。ただし、出力ビームの強度は、任意の横位置 (x, y) で入射ビームのそれを超えることはできませんと振幅の形成によって部分的に有害の干渉により発生した強度損失されます。
エンコード方法7に下線を引く理論は次のとおりです。U(x,y)= A(x,y)e私φ(x,y)の形式で表される任意の複雑なフィールドはまたとして書き換えることができます。
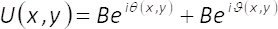 (1)
(1)
どこ
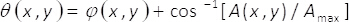 (2)
(2)
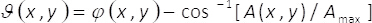 (3)
(3)
方程式 1-3、振幅と位相の二次元コンプレックスのフィールド、 U(x,y)は A によって与えられる(x,y) とφ(x,y) はそれぞれ。注意: 条件、max ( A(x,y) の最大) とB = 、max/2 は横の座標に依存しない (x、y)。我々 が設定されている場合は、理論から、最大2、B = =1。したがって、複雑なフィールド U(x,y) が得られ、単純な方法で、均一な波が私ϑ(x,y)とのコヒーレント和からiθ (x,y)。実習では、これは、単相要素α(x,y)、イメージング システムの入力平面に配置されて成っているコモンパス干渉計によって行われます。フェーズ条件ϑ(x,y) の空間多重化により単相要素の作成します。
θ(x,y) 二次元バイナリ格子 (チェッカー ボードのパターン) の助けを借りてM1(x,y) とM2(x,y) 次のように
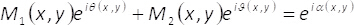 (4)
(4)
それ故に、
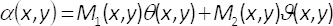 (5)
(5)
これらのバイナリ パターンを満たす条件M1(x,y) + M2(x,y) = 1。我々 は位相要素α(x,y) に含まれる情報を混在させないでください場合均一な波の干渉が発生しないことを注意してください。現在のメソッドでこれは回折のすべての注文が 0 番目のものをブロックすることが空間フィルターを用いた実施です。フーリエ面、スペクトルH(u,v) でフィルター処理した後、この方法でF ={eiα(x,y)} のエンコードされた相関数は、式で複雑なフィールドF{U(x,y)} のスペクトルに関連します。
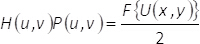 (6)
(6)
式 (6) に (u、v)周波数領域の座標を意味するP(u,v) を保持する空間のフィルターでは、特定の関数Θ(x,y) のフーリエ変換の形で表されるに対しF{Θ(x,y)}。Eq (6) からそれは次のとおり (恒常的要因を考慮した) することがなく取得した複雑なフィールドURET(x、y)、イメージング システムの出力面で、拡大と空間的畳み込みによって与えられるフィルター マスクのフーリエ変換と逆に複雑なフィールドU(x,y)。それです:
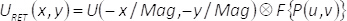 (7)
(7)
記号で示されます畳みこみ演算式 (7)、 とマグは、イメージング システムの倍率を表す用語。したがって、振幅とU(x,y) の位相が完全に畳み込み操作による空間解像度のいくつかの損失を除いて、出力面で取得されます。
とマグは、イメージング システムの倍率を表す用語。したがって、振幅とU(x,y) の位相が完全に畳み込み操作による空間解像度のいくつかの損失を除いて、出力面で取得されます。
Access restricted. Please log in or start a trial to view this content.
プロトコル
1. 単相要素に複雑なフィールドをエンコード
- SLM の技術仕様からその空間分解能 (例えば 1920 ピクセル x 1800 ピクセル) を見つけます。
- 定義し、望ましい振幅A(x,y) とデジタル画像として位相φ(x,y) パターンを生成します。
- デジタル画像は SLM 表示と同じ上記の空間分解能を設定します。
- 灰色のレベル形式で上記画像を設定します。
- 振幅と位相画像の最小値と最大値 255、0 から π/2、π/2 にそれぞれ設定します。
- 設定、最大= 方程式 2 と 3、2 と位相パターンϑ(x,y) およびθ(x,y) からコンピューター生成します。
- コンピューターは、 M1(x,y) とM2(x,y) のチェッカー ボード パターンを生成します。
- これらのチェッカー ボード パターンの空間分解能は SLM 表示に設定します。
- ピクセルのクロストークの影響を減らすためには、チェッカー ボード パターンM1(x,y) とM2(x,y) を持つ別のピクセル セルで構成の他のペアを生成します。ピクセルの数が増加 (例えば: 2 × 2、3 × 3、4 × 4 の画素セル等)。
注意: 画素セルを増やすときチェッカー ボード パターンのピクセルの総数保たれなければならない変更されずに、SLM の空間分解能に等しい。最終的なすべてのチェッカー ボード パターンのピクセル数は、画素セルを変更した後は同じを確認します。
- コンピューターは、式 5 から単相要素α(x,y) を生成します。
注: は、このプロトコルの手順 1 に関連するタスクの補足素材「MATLAB_code_1.m」を参照してください。
2. 複雑な分野の復興
- 光源として平行、直線偏光と空間コヒーレント レーザー ビームを使用します。
- 少なくともと位相限定 SLM を使用して 2 π 位相範囲。
- 必要なときは、SLM の表示サイズにビームのサイズを調整するのに適切なビーム エキスパンダーを使用します。
- 必要に応じて、レーザー ビームの偏極を水平方向に設定するのに光の偏光板を使用します。これ通常位相限定 SLMs、通常水平方向に振動する電磁界の空間位相を調節するため設計された、その垂直成分をそのまま維持の適切な操作のために重要です。
- SLM に位相パターンを送信するために接続、制御コンピューターと SLM に SLM の製造元によって与えられる標準的な通信プロトコルに従います。
注: この目的のための共通のプロトコルには、SLM の電子制御ユニットの電圧レベルに変換されます最終的に灰色レベルのもの、(のために角度の数値演算) ラジアン値に変換する校正曲線の使用が含まれています。また、SLM は、独自の画面を持つ外部デバイスとしてコンピューターに接続されて、コンピューター画面の拡張は通常、必要に応じてだけでなく、この余分な画面に対応する階調画像を送信する適切なプログラム。これらのコード例は、補足資料として含まれています (MATLAB_code_2.m を参照してください)。 - 画像光学システムを実装し、このシステムの入力平面に SLM のモニターを設置します。
- (4fの光学系は、このタスクに対して有効) 2f x 2f光学画像システムの構築に焦点距離fの屈折レンズを使用します。複雑なフィールド、ビーム幅、光の波長、物理容量の予想出力サイズに基づき最適の技術仕様(例えば、コーティング、サイズ、焦点距離等)とレンズ/レンズを採用してください。
- 検索するイメージング システムの出力面の位置を SLM に位相パターンα(x,y) を送信して視覚的に (カメラの位置) によって記録された画像の最高の空間分解能で。
注意: 低サイズ画素セル (たとえば、1 x 1 ピクセル セル) と SLM 表示ピクセル幅数ミクロン (例えば、8 μ m) の場合ビーム伝搬だけ作り出すことができるエンコードされた均一な波、再構成画像を得ること間の干渉イメージング システムに、アイリスを含めて。低サイズ画素セルを使用して、出力面の位置を探します。 - 光学系のフーリエ面に可変直径の円形虹彩を置き、レーザ光線の焦点の中心を合わせます。
- フーリエ面で、アイリスのサイズを調整するには、位相パターンα(x,y) を送信し、最高空間分解能 (円形虹彩の直径) によって記録される画像の視覚的に見えます。
注意: 長いサイズ ピクセル セル (たとえば、4 x 4 画素セル) の場合エンコードされた均一な波との干渉は基本的に実施空間フィルター。円形絞りのサイズを調整するのに長いサイズの画素セルを使用します。このプロトコル用語低サイズ、長いサイズ、画素セル内に含まれるピクセル数に呼ばれます。ただし、上記の干渉はピクセルの幅にも依存します。ピクセル幅の等しいまたはより小さい 8 μ m SLMs を採用してください。
- 位相要素α(x,y) SLM に対応する濃淡画像を送信します。
- クロストークの影響を最小限に抑え、高い空間分解能で記録された画像を実現できる最高画素セルサイズを探します。
3. 再構築された複雑なフィールドを測定します。
- 偏光を用いた位相シフト露光法8を実装します。
- 置き、SLM の手前にある、最初の偏光の回転角度に合わせます (図 2参照)。最初の偏光板の回転角度を設定すると、視覚的に CCD カメラ (イメージング システムの出力平面に配置されて)、偏光板の回転に応じての最大値と最小光透過性を確認します。偏光板の 2 つの対応する角度を書き留めます。2 つの以前に記録された角度の間に偏光板の最終的な角度を修正します。
- 配置し、イメージング システムのフーリエ面の後にある、第 2 の偏光の回転角度に合わせます (図 2参照)。2 つ目の偏光板の回転角度を設定するのには SLM に位相パターンα(x,y) を送信した後 (イメージング システムの出力平面に配置されて) CCD カメラで最もぼやけと鮮明な画像を見て視覚的に。偏光板の 2 つの対応する角度を書き留めます。以前に記録された角度の間に 2 つ目の偏光板の最終的な角度を修正します。
- レコード、インターフェロ。
- イメージング システムの出力面で CCD カメラをしてください。
- 最初インターフェロ グラムを記録するには、位相要素α(x,y) に 0 のラジアンのマトリックスを追加し、それを SLM に送信します。レコードの対応するイメージ私1(x,y)、ccd。
- 2 番目のインターフェロ グラムを記録するには、位相要素α(x,y) に π/2 ラジアンのマトリックスを追加し、それを SLM に送信します。レコードの対応するイメージ私2(x,y) CCD カメラで。
- 3 インターフェロ グラムを記録するには、位相要素α(x,y) に π のラジアンのマトリックスを追加し、それを SLM に送信します。レコードの対応するイメージ私3(x,y) CCD カメラで。
- 4 番目と最後の干渉を記録、位相要素α(x,y) に 3 π/2 ラジアンのマトリックスを追加し、SLM に送信します。レコードの対応するイメージ私4(x,y) CCD カメラで。
- 複雑なフィールドを再構築します。
注: プロトコルのこのポイントに関連するタスクの補足素材「MATLAB_code_3.m」を参照してください。- 式を使用して、(x,y)の取得を複雑なフィールドの振幅を取得します。
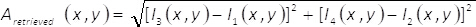 (8)
(8) - 式を使用して、(x,y) φ取得複雑なフィールドのフェーズを取得します。
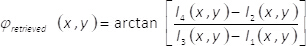 (9)
(9)
- 式を使用して、(x,y)の取得を複雑なフィールドの振幅を取得します。
Access restricted. Please log in or start a trial to view this content.
結果
採用フェーズ専用の SLM の空間分解能は 1920 ピクセル x 1080 ピクセル、8 μ m の画素ピッチを持つ。選択した振幅A(x,y) と位相φ(x,y) 複雑なフィールドのよく知られているレナの画像 (振幅パターン) と若い女の子に対応する 2 つの異なる灰色レベルのイメージによって定義されます。それぞれ (位相パターン)、彼女の舌を突き出し?...
Access restricted. Please log in or start a trial to view this content.
ディスカッション
このプロトコルでは位相限定 SLM またはコンピューター生成パターンの画素セルに含まれるピクセル数の幅をピクセル単位として実用的なパラメーターは正常にエンコード方式を実装するための重要なポイントです。手順 1.2、1.3、1.4 プロトコル、ピクセル幅が短ければ短いほどよりの空間解像度の取得した振幅と位相のパターンにまた、SLM に突然ピクセル-位相変調の成文化は、予期しない?...
Access restricted. Please log in or start a trial to view this content.
開示事項
著者が明らかに何もありません。
謝辞
この研究は Generalitat (プロメテオ 2016年-079)、大学ジャウメ 1 によって支えられた私 (宇治) (UJIB2016-19);Ministerio デ Economía y Competitividad (MINECO) (FIS2016-75618-R)。著者が大学ジャウメの SCIC に非常に感謝して私のフェムト秒レーザーの使用のため。
Access restricted. Please log in or start a trial to view this content.
資料
| Name | Company | Catalog Number | Comments |
| Achromatic Doublet | THORLABS | AC254-100-B-ML | Lens Diameter 25.4 mm, focal length 100 mm |
| Achromatic Galilean Beam Expander | THORLABS | GBE05-A | AR Coated: 400 - 650 nm |
| Basler camera | BASLER | avA1600-50gm GigE camera | sensor size 8.8 mm x 6.6 mm, pizel size 5.5 microns |
| Mounted Zero-Aperture Iris | THORLABS | ID12Z/M | Max Aperture 12 mm |
| Pellicle Beamsplitter | THORLABS | CM1-BP145B2 | 45:55 (R:T), Coating: 700 - 900 nm |
| PLUTO Spatial Light Modulator | HOLOEYE Photonics AG | NIR-II | Phase Only Spatial Light Modulator (Optimized for 700 -1000 nm) |
| Two thin film laser polarizers | EKSMA OPTICS | 420-0526M | material BK7, diameter 50 mm, wavelength 780-820 nm |
参考文献
- Hsueh, C. K., Sawchuk, A. A. Computer-generated double-phase holograms. Applied Optics. 17 (24), 3874-3883 (1978).
- Arrizón, V. Complex modulation with a twisted-nematic liquid-crystal spatial light modulator: double-pixel approach. Optics Letters. 28 (15), 1359-1361 (2003).
- Arrizón, V., Ruiz, U., Carrada, R., González, L. A. Pixelated phase computer holograms for the accurate encoding of scalar complex fields. Journal of the Optical Society of America A. 24 (11), (2007).
- Shibukawa, A., Okamoto, A., Takabayashi, M., Tomita, A. Spatial cross modulation method using a random diffuser and phase-only spatial light modulator for constructing arbitrary complex fields. Optics Express. 22 (4), 3968-3982 (2014).
- Martínez-Fuentes, J. L., Moreno, I. Random technique to encode complex valued holograms with on axis reconstruction onto phase-only displays. Optics Express. 26 (5), 5875-5893 (2018).
- Clark, T. W., Offer, R. F., Franke-Arnold, S., Arnold, A. S., Radwell, N. Comparison of beam generation techniques using a phase only spatial light modulator. Optics Express. 24 (6), 6249-6264 (2016).
- Mendoza-Yero, O., Mínguez-Vega, G., Lancis, J. Encoding complex fields by using a phase-only optical element. Optics Letters. 39 (7), 1740-1743 (2014).
- Yamaguchi, I., Zhang, T. Phase-shifting digital holography. Optics Letters. 22 (16), 1268-1270 (1997).
- Shao, Y., et al. Addressable multiregional and multifocal multiphoton microscopy based on a spatial light modulator. Journal of Biomedical Optics. 17 (3), 030505(2012).
- Mendoza-Yero, O., Carbonell-Leal, M., Mínguez-Vega, G., Lancis, J. Generation of multifocal irradiance patterns by using complex Fresnel holograms. Optics Letters. 43 (5), 1167-1170 (2018).
- Kuang, Z., et al. Diffractive Multi-beam Ultra-fast Laser Micro-processing Using a Spatial Light Modulator (Invited Paper). Chinese Journal of Lasers. 36 (12), 3093-3115 (2009).
- Kuang, Z., et al. High throughput diffractive multi-beam femtosecond laser processing using a spatial light modulator. Applied Surface Science. 255, 2284-2289 (2008).
Access restricted. Please log in or start a trial to view this content.
転載および許可
このJoVE論文のテキスト又は図を再利用するための許可を申請します
許可を申請さらに記事を探す
This article has been published
Video Coming Soon
Copyright © 2023 MyJoVE Corporation. All rights reserved