JoVE 비디오를 활용하시려면 도서관을 통한 기관 구독이 필요합니다. 전체 비디오를 보시려면 로그인하거나 무료 트라이얼을 시작하세요.
Method Article
진폭 및 위상 레이저 광선의 위상 전용 공간 가벼운 변조기를 사용 하 여 형성
요약
우리는 단일 위상 요소를 사용 하 여 레이저 광선의 복잡 한 필드를 인코딩하는 방법을 보여 줍니다. 공통 경로 간섭계는 위상 전용 공간 가벼운 변조기 마침내 광학 이미징 시스템의 출력에서 원하는 복잡 한 필드 패턴을 검색 하로 표시 되는 단계 정보를 혼합 채택 된다.
초록
이 글의 목표는 시각적으로 일관 된 레이저 방사와 관련 된 복잡 한 필드를 인코딩 하는 간섭 방법의 활용을 보여 줍니다. 메서드는 이전 그들의 단계의 공간 다중화는 위상 전용 공간 광 변조기 (SLM)로 인코딩 두 개의 균일 한 파도의 일관 된 합계를 기반으로 합니다. 여기, 간섭 과정 특정 이미징 시스템의 푸리에 비행기에 빛 주파수의 공간 필터링에 의해 수행 됩니다. 이 방법의 올바른 구현에는 임의 위상 및 진폭 정보는 광학 시스템의 출력에서 검색할 수 있습니다.
그것 보다는 꺼짐-축-축, 인코딩 기법, 직접 처리 알고리즘 (반복 루프 하지), 그리고 일관 된 잡음 (얼룩)에서 무료. 복잡 한 필드 주파수 필터링 프로세스로 인해 해상도의 일부 손실 제외 광학 시스템의 출력에서 정확 하 게 검색할 수 있습니다. 방법의 주요 한계는 SLM의 새로 고침 속도 보다 더 높은 주파수에 작동 하는 무 능력에서 올 수도 있습니다. 응용 프로그램에 포함 되지만, 선형 및 비선형 현미경, 빔 형성, 또는 레이저 마이크로 가공 소재 표면에 국한 되지 않습니다.
서문
거의 모든 레이저 응용 프로그램 빛의 광 파면의 관리와 가까운 관계에 있다. Paraxial 근사에서 레이저 방사와 관련 된 복잡 한 필드는 2 개의 기간, 진폭 및 단계에 의해 설명할 수 있습니다. 이 두 학기 동안 제어 하는 데는 측 두 엽과에 레이저 광선의 공간 구조를 수정 하는 데 필요한 것입니다. 일반적으로, 진폭 및 위상 레이저 광선의 변경할 수 있습니다 제대로 광학 부품의 사용을 포함 하 여 여러 가지 방법에 의해 그 범위 단일 대량 렌즈, 빔 스플리터와 거울에서 deformable 거울 또는 공간 빛 같은 가장 복잡 한 장치 변조기입니다. 여기, 우리가 인코딩 및 듀얼 위상 홀로그램 이론1에 근거 하는 일관 된 레이저 광선의 복잡 한 분야 그리고 공통 경로 간섭계의 사용률을 재구성 하는 방법을 보여줍니다.
요즘, 다양 한 레이저 광선2,3,,45의 복잡 한 필드를 인코딩하는 방법 존재 합니다. 이러한 맥락에서 위상 및 진폭 변조를 생산 하 몇 가지 잘 설립 방법이 디지털 홀로그램6의 사용에 의존. 이러한 모든 방법에 일반적인 포인트 SLM 디스플레이에서 빛의 반사에서 오는 zeroth 순서에서 원하는 출력 빔 분리 공간 오프셋 생성의 필요성입니다. 이 메서드는 기본적으로 꺼짐-축 (일반적으로 격자의 첫 번째 회절 순서에 대 한 적용), 위상 격자 인코딩하는 단계에 뿐만 아니라 소개 뿐만 아니라 필요한 진폭 변조를 채용. 특히, 진폭 변조는 공간적으로 명확 하 게 회절 효율을 저하 하는 격자 높이 낮추는 방법으로 수행 됩니다. 홀로그램 재건 과정 대부분의 진폭과 위상 원하는 복잡 한 필드의 대략적인, 하지만 하지 정확한 재건을 가져옵니다. 이론과 실험 사이 불일치 진폭 정보 뿐만 아니라 다른 실험 문제 SLM pixilation 효과 또는 첫 번째 회절 순서의 공간 필터링 하는 동안 일어나는 부정확 한 인코딩을 표시 하는 것 같다. 또한, 입력된 광속의 강도 프로필 출력에 제한이 발생할 수 있습니다.
대조적으로, 도입된 방법7모든 빛 관리 수행 됩니다 축에는 실험적인 관점에서 매우 편리 하다. 또한, 그것은 paraxial 근사에서 두 개의 균일 한 파의 합으로 레이저 빔과 관련 된 복잡 한 필드를 고려 합니다. 진폭 정보는 이러한 균일 한 파의 간섭에 의해 synthetized. 실제로, 이러한 간섭 이미징 시스템의 푸리에 비행기에 빛 주파수의 공간 필터링에 의해 수행 됩니다. 이전, 균일 한 파도와 관련 된 위상 패턴 공간 다중화 되며 단계 전용 SLM (이 이미징 시스템의 입구 평면에 배치)으로 인코딩된. 따라서, 전체 광학 설치 공통 경로 간섭계 (기계적 진동, 온도 변화, 또는 광학 부정합에 대 한 매우 강력한)으로 간주 될 수 있습니다. 참고로 상술 간섭 과정 또는 다른 광학 레이아웃을 사용 하 여 달성 될 수 있다: 일반적인 2-팔 간섭계 내에서 또는 시간 순차적으로 인코딩 하 여 제대로 배치 하는 위상 전용 SLMs의 부부와 함께 2 단계 SLM (광학 설치 참조 거울의 이전 도입)으로 패턴. 두 경우 모두, 공간 필터링의 필요성 및 따라서 맞춤 과정 뿐만 아니라 광학 시스템의 복잡성을 증가 비용 공간 해상도의 손실 없이 있다. 여기, 그것은 강조 되어야 한다 또한이 인코딩 메서드를 사용 하 여 원하는 복잡 한 필드의 전체 스펙트럼 수 있는 푸리에 평면에 정확 하 게 검색 을 필터링 모든 회절 주문 하지만 하나 영 후.
다른 한편으로, 방법의 효율성 여러 가지 요인에 따라 달라 집니다: SLM (예를 들어, 채우기 비율, 반사도, 또는 회절 효율)는 빛에 impinges 방식과 인코딩된 패턴의 크기의 제조업체의 사양에 SLM (작은 타격 각도와 빔 스플리터를 사용 하 여 정상적인 부각 반사). 이 시점에서, 적절 한 실험 조건 하에서 측정 된 총 빛 효율 30% 이상 수 있습니다. 그러나, 단지는 SLM의 사용으로 인해 총 광 효율 50% 미만 수 있는 note. 부족 또는 기관총 요소는 광학 설치 일관 된 잡음 (얼룩) 없이 진폭과 위상 패턴의 검색 수 있습니다. 다른 중요 한 측면을 지적 하는 직접 법전 편찬 알고리즘의 활용 보다는 반복적인 절차 및 임의적이 고 독립적인 진폭과 주파수에서 위상 변조를 수행 하는 기능 새로 고침는 SLM의 시간 (를 현재의 기술에 따라 헤르츠의 수백).
원칙적으로, 방법7 입력된 비행기 파도 함께 사용 될 것입니다 하지만 그것에 국한 되지 않습니다. 예를 들어, 가우스 빔은 SLM 타격 이다, 하는 경우는 SLM에 적합된 진폭 패턴을 인코딩하여 시스템의 출력에서 방사 모양을 수정 가능 하다. 그러나, 출력 빔 강도 어떤 횡단 위치에서 (x, y) 입력된 광속의 초과 수 없습니다, 부분적으로 파괴적인 간섭 과정에 의해 유래 강도 손실에 의해 수행 됩니다 진폭의 형성.
인코딩 방법7 밑줄 이론은 다음과 같습니다. U(x,y) (x,y)A =eiφ(x,y) 형태로 나타내는 어떤 복잡 한 필드도로 다시 작성할 수 있습니다.
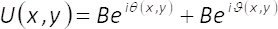 (1)
(1)
어디
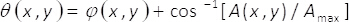 (2)
(2)
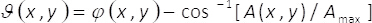 (3)
(3)
방정식 1-3에서에서 진폭과 위상의 2 차원 복잡 한 필드 U(x,y)A에 의해 주어진 다(x,y) 및 φ(x,y), 각각. 유의 기간 을최대 ( A(x,y)의 최대) 및 B = 는최대/2 횡단 좌표에 의존 하지 않는 (x,y). 이론, 우리가 설정에서 는최대2, B = =1. 따라서, 복잡 한 필드 U(x,y) 간단한 방법으로 얻을 수 있다, 균일 한 파도 수난ϑ(x,y) 및 의 일관 된 합계에서 수 iθ (x,y). 실제로,이는 단일 위상 요소 α(x,y), 이미징 시스템의 입력된 평면에 배치로 이루어진 공통 경로 간섭계와 함께 수행 됩니다. 단일 위상 요소 단계 용어 ϑ(x,y)의 공간 다중화 구성
그리고 θ (x,y) 2 차원 이진 격자 (바둑판 패턴)의 도움으로 M1(x,y)과 M2(x,y) 다음과 같이
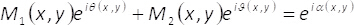 (4)
(4)
따라서,
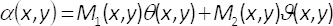 (5)
(5)
이러한 바이너리 패턴 충족 조건 (x,y) M1+ M2(x,y) = 1. Note, 균일 한 파의 간섭 우리가 위상 요소α(x,y)에 포함 된 정보를 혼합 하지 마십시오 경우 일어날 수 없다. 현재 메서드에서이 모든 회절 주문 하지만 하나 영 차단할 수 공간 필터를 사용 하 여 수행 됩니다. 이 방법에서는, 푸리에 비행기, 스펙트럼 H(u,v)에 필터링 프로세스 후F ={eiα(x,y)} 인코딩된 위상의 식으로 복잡 한 필드 F의 스펙트럼 {U(x,y)} 관련 함수
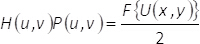 (6)
(6)
식 (6)에 (u,v) 나타내는 좌표 주파수 영역에서 P(u,v) 공간 필터에 대 한 보유 푸리에 변환 지정된 함수 Θ(x,y)의 형태로 표현 하는 반면 F {Θ(x,y)}. Eq. (6)에서 그것, 이미징 시스템, 검색 된 복잡 한 필드 URET(x,y), (일정 한 요소를 고려한)의 출력 평면에 따른다, 회선의는 확대 및 공간에 의해 주어진 다 필터 마스크의 푸리에 변환으로 복잡 한 필드 U(x,y)를 반전. 말하자면:
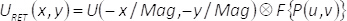 (7)
(7)
식 (7), 회선 작업 기호 표시 됩니다  , 그리고 매기 이미징 시스템의 확대를 나타내는 용어. 따라서, 진폭과 위상 U(x,y)의 완전히 출력 비행기 때문에 회선 작업 공간 해상도의 일부 손실 제외에서 검색 됩니다.
, 그리고 매기 이미징 시스템의 확대를 나타내는 용어. 따라서, 진폭과 위상 U(x,y)의 완전히 출력 비행기 때문에 회선 작업 공간 해상도의 일부 손실 제외에서 검색 됩니다.
Access restricted. Please log in or start a trial to view this content.
프로토콜
1. 단일 위상 요소에 복잡 한 필드 인코딩
- SLM의 기술 사양에서 그것의 공간적 해상도 (예를 들어 1920 픽셀 x 1800 픽셀)을 찾아.
- 정의 하 고 원하는 진폭 A(x,y) 및 위상 φ(x,y) 패턴으로 디지털 이미지를 생성.
- 설정 상술의 공간 해상도 디지털 이미지의 SLM 디스플레이.
- 상기 디지털 이미지 회색 레벨 형식으로 설정 합니다.
- 진폭 및 위상 이미지의 최소 및 최대 값 0 ~ 255, 그리고 π/2,-π/2에서 각각 설정.
- 최대 설정에서 식 2 및 3, 2 = 및 위상 패턴 ϑ(x,y)와 θ(x,y) 그들 로부터 컴퓨터 생성.
- 컴퓨터는 바둑판 패턴 M1(x,y)과 M2(x,y)를 생성 합니다.
- SLM 디스플레이의 동등이 바둑판 패턴의 공간 해상도 설정 합니다.
- 픽셀 크로스 토크의 효과 줄이기 위해, 바둑판 패턴 M1(x,y)과 M2(x,y) 다른 픽셀 셀 데 건설의 다른 쌍을 생성 한 픽셀의 수를 증가 (예를 들면: 2 x 2, 3 x 3, 및 4 x 4 픽셀 셀, 등).
주의: 픽셀 셀 증가, 바둑판 패턴의 픽셀의 총 수 유지 되어야 한다 변경 하 고는 SLM의 공간 해상도 같아집니다. 그 모든 바둑판 패턴의 픽셀의 최종 번호 동일 그들의 픽셀 셀 수정 후 확인 합니다.
- 컴퓨터 식 5에서에서 단일 위상 요소 α(x,y)를 생성 합니다.
주:이 프로토콜의 1 단계에 관련 된 작업에 대 한 "MATLAB_code_1.m" 라는 보충 자료를 참조 하십시오.
2입니다. 복잡 한 필드의 재건
- 광원 조명을, 선형 편광, 그리고 공간적으로 일관 된 레이저 광선을 사용 합니다.
- 이상으로 위상 전용 SLM을 사용 하 여 2 π 단계 범위.
- 필요한 경우 적절 한 빔 익 스팬 더를 사용 하 여 SLM 디스플레이의 크기에 광속의 크기를 조정.
- 필요한 경우 수평 방향으로 레이저 빔 편광을 설정 하는 광학 편광판을 사용 합니다. 이것은 일반적으로 위상 전용 SLMs, 일반적으로 수평 방향으로 진동 하는 전자기장의 공간적 위상 변조 하도록 설계 되었습니다, 수직 구성 그대로 유지의 적절 한 작동을 위해 중요 한.
- SLM에 위상 패턴을 보내기 위해 연결 하 고 제어 컴퓨터와 SLM SLM의 제조 업체에 의해 주어진 표준 통신 프로토콜을 따릅니다.
참고:이 목적을 위해 일반적인 프로토콜은 SLM의 전자 제어 장치는 마지막으로 전압 레벨 변환 회색 수준, (때문에 각도와 수학 연산) 라디안에서 값을 변환 하기 위해 보정 곡선의 사용을 포함 합니다. 또한,는 SLM 자체 화면 외부 장치로 컴퓨터에 연결 되어, 컴퓨터 스크린의 확장은 일반적으로 해당 회색 레벨 이미지 추가 화면을 보낼 적절 한 프로그램으로 필요한. 이러한 코드의 예로 또한 보충 자료로 포함 된다 (, 보십시오 MATLAB_code_2.m). - 이미지 광학 시스템을 구현 하 고이 시스템의 입력된 비행기에는 SLM의 표시를 넣어.
- 초점 거리 f 의 굴절 렌즈를 사용 하 여 (4f 광학 시스템은 또한이 작업에 대 한 유효) 2f x 2f 광학 이미지 시스템 구축. 복잡 한 필드, 빔 폭, 빛의 파장 및 사용 가능한 실제 공간의 예상된 출력 크기에 따라 적합 한 기술 사양 (예: 코팅, 크기, 초점, 등)와 렌즈/렌즈를 사용 합니다.
- 이미징 시스템의 출력 비행기의 위치를 찾을 수는 SLM에 위상 패턴 α(x,y)을 보내고 최고의 공간 해상도 (카메라의 위치)에 따라 기록 된 이미지에 대 한 시각적으로 보고 하십시오.
주의: 낮은 크기 픽셀 셀 (예를 들어, 1 x 1 픽셀) 및 픽셀 폭이 몇 미크론 (예를 들어, 8 µ m)의 SLM 디스플레이, 빔 전파만 생성할 수 있습니다 복원 이미지 인코딩된 유니폼 파도 사이의 간섭 없이 원형 조리개를 포함 하 여 이미징 시스템에. 저 크기 픽셀 셀을 사용 하 여 출력 비행기의 위치를 찾습니다. - 광학 시스템의 푸리에 평면에서 가변 직경의 원형 조리개를 놓고 레이저 빔 초점의 그것의 센터를 정렬 합니다.
- 푸리에 비행기에서 원형 조리개의 크기를 조정 하려면 단계 패턴 α(x,y)를 보내 하 고 시각적으로 최고의 공간 해상도 (원형 조리개의 지름)에 따라 기록 된 이미지에 대 한 보고.
주의: 긴 크기 픽셀 셀 (예를 들어, 4 x 4 픽셀), 경우 인코딩된 동일한 파 사이 방해는 기본적으로 실시 공간 필터. 원형 조리개의 크기를 조정 하려면 긴 크기 픽셀 셀을 사용 합니다. 이 프로토콜에서 용어 낮은 크기와 긴 크기 픽셀 셀에 포함 된 픽셀의 수 이라고 합니다. 그러나, 상기 간섭 또한 픽셀 너비에 따라 다릅니다. 픽셀 너비 동등 또는 미만 8 µ m SLMs를 사용 합니다.
- 회색 수준 이미지에 해당 하는 위상 요소 α(x,y)는 SLM을 보냅니다.
- 혼선 효과 최소화 하기 위해 기록 된 이미지에서 더 높은 공간적 해상도 달성 수 있는 최고의 픽셀 셀 크기를 찾고 있습니다.
3. 복원 된 복잡 한 필드 측정
- 분극 기반 위상 변화 기법8을 구현 합니다.
- 놓고는 SLM의 바로 전에 있는 첫번째 광학 편광의 회전 각도 맞춥니다 ( 그림 2참조). 첫 번째 편광판의 회전 각도 설정 하려면 CCD 카메라 (이미징 시스템의 출력 평면에 배치), 편광판의 회전에 따라 최대 및 최소한의 빛 투과율을 찾고 시각적으로 있습니다. 편광판의 두 해당 각도 적어 둡니다. 두 이전 기록 각도 사이에 편광판의 최종 각도 수정 합니다.
- 장소 및 이미징 시스템의 푸리에 비행기 후 두 번째 광학 편광의 회전 각도 맞춥니다 ( 그림 2참조). 두 번째 편광판의 회전 각도 설정 하려면 시각적으로 찾습니다 (이미징 시스템의 출력 평면에 배치) CCD 카메라의 날카로운와 가장 흐린 이미지는 SLM에 위상 패턴 α(x,y)를 보낸 후. 편광판의 두 해당 각도 적어 둡니다. 그 이전 기록 각도 사이 두 번째 편광판의 최종 각도 수정 합니다.
- 레코드는 interferograms입니다.
- 이미징 시스템의 출력 평면에 CCD 카메라를 계속.
- 첫 번째 interferogram 기록, 위상 요소 α(x,y)에 0 라디안의 매트릭스를 추가 하 고는 SLM 보내기. 레코드 해당 이미지 나1(x,y)는 CCD와 함께.
- 두 번째 interferogram 기록, 위상 요소 α(x,y)를 π/2 라디안의 매트릭스를 추가 하 고는 SLM 보내기. 레코드 해당 이미지 난2(x,y) CCD 카메라와 함께.
- 제 3 interferogram를 기록, 위상 요소 α(x,y)를 π 라디안의 매트릭스를 추가 하 고는 SLM 보내기. 레코드 해당 이미지 내가3(x,y) CCD 카메라와 함께.
- 제 4 그리고 마지막 interferogram를 기록, 위상 요소 α(x,y)를 3 π/2 라디안의 매트릭스를 추가 하 고는 SLM 보내기. 레코드 해당 이미지 나4(x,y) CCD 카메라와 함께.
- 복잡 한 필드를 재구성 합니다.
주: 프로토콜의이 시점에서 관련된 작업에 대 한 "MATLAB_code_3.m" 라는 보충 자료를 참조 하십시오.- 식을 사용 하 여 복잡 한 필드 (x,y) 검색의 검색
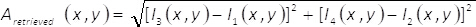 (8)
(8) - 복잡 한 필드 (x,y) φ검색의 단계는 식을 사용 하 여 검색
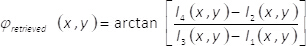 (9)
(9)
- 식을 사용 하 여 복잡 한 필드 (x,y) 검색의 검색
Access restricted. Please log in or start a trial to view this content.
결과
고용된 단계 전용 SLM의 공간 해상도 8 µ m의 픽셀 피치 1920 픽셀 x 1080 픽셀입니다. 선택 된 진폭 A(x,y) 및 위상 φ(x,y) 복잡 한 필드의 두 가지 회색 레벨 이미지 잘 알려진 Lenna 그림 (진폭 패턴)와 젊은 여자에 의해 정의 됩니다. 그녀의 혀 (위상 패턴), 밖으로 튀어나와 각각. 일반적으로, 필요한 패턴의 세대와는 SLM의 제어, Matlab 코드 ?...
Access restricted. Please log in or start a trial to view this content.
토론
이 프로토콜에는 위상 전용 SLM 또는 컴퓨터에서 생성 된 패턴의 픽셀 셀에 포함 된 픽셀 수의 픽셀 폭으로 실용적인 매개 변수 인코딩 메서드를 성공적으로 구현 하는 핵심 포인트는. 단계 1.2, 1.3, 1.4 프로토콜, 짧은 픽셀 너비, 더 나은 공간적 해상도의 검색 된 진폭 및 위상 패턴의. 또한, 갑작스러운 픽셀 위상 변조는 SLM에 법전 편찬 예기치 않은 위상 응답 (픽셀 누화) 발생 한 수 있습니다로 바둑...
Access restricted. Please log in or start a trial to view this content.
공개
저자는 공개 없다.
감사의 말
이 연구는 Generalitat 발렌시아 (PROMETEO 2016-079), Universitat Jaume에 의해 지원 되었다 내가 (우) (UJIB2016-19); 그리고 정부의 드 Economía y Competitividad (MINECO) (FIS2016-75618-R). 저자는 매우 감사 Universitat Jaume SCIC 펨 레이저의 사용에 대 한 나.
Access restricted. Please log in or start a trial to view this content.
자료
| Name | Company | Catalog Number | Comments |
| Achromatic Doublet | THORLABS | AC254-100-B-ML | Lens Diameter 25.4 mm, focal length 100 mm |
| Achromatic Galilean Beam Expander | THORLABS | GBE05-A | AR Coated: 400 - 650 nm |
| Basler camera | BASLER | avA1600-50gm GigE camera | sensor size 8.8 mm x 6.6 mm, pizel size 5.5 microns |
| Mounted Zero-Aperture Iris | THORLABS | ID12Z/M | Max Aperture 12 mm |
| Pellicle Beamsplitter | THORLABS | CM1-BP145B2 | 45:55 (R:T), Coating: 700 - 900 nm |
| PLUTO Spatial Light Modulator | HOLOEYE Photonics AG | NIR-II | Phase Only Spatial Light Modulator (Optimized for 700 -1000 nm) |
| Two thin film laser polarizers | EKSMA OPTICS | 420-0526M | material BK7, diameter 50 mm, wavelength 780-820 nm |
참고문헌
- Hsueh, C. K., Sawchuk, A. A. Computer-generated double-phase holograms. Applied Optics. 17 (24), 3874-3883 (1978).
- Arrizón, V. Complex modulation with a twisted-nematic liquid-crystal spatial light modulator: double-pixel approach. Optics Letters. 28 (15), 1359-1361 (2003).
- Arrizón, V., Ruiz, U., Carrada, R., González, L. A. Pixelated phase computer holograms for the accurate encoding of scalar complex fields. Journal of the Optical Society of America A. 24 (11), (2007).
- Shibukawa, A., Okamoto, A., Takabayashi, M., Tomita, A. Spatial cross modulation method using a random diffuser and phase-only spatial light modulator for constructing arbitrary complex fields. Optics Express. 22 (4), 3968-3982 (2014).
- Martínez-Fuentes, J. L., Moreno, I. Random technique to encode complex valued holograms with on axis reconstruction onto phase-only displays. Optics Express. 26 (5), 5875-5893 (2018).
- Clark, T. W., Offer, R. F., Franke-Arnold, S., Arnold, A. S., Radwell, N. Comparison of beam generation techniques using a phase only spatial light modulator. Optics Express. 24 (6), 6249-6264 (2016).
- Mendoza-Yero, O., Mínguez-Vega, G., Lancis, J. Encoding complex fields by using a phase-only optical element. Optics Letters. 39 (7), 1740-1743 (2014).
- Yamaguchi, I., Zhang, T. Phase-shifting digital holography. Optics Letters. 22 (16), 1268-1270 (1997).
- Shao, Y., et al. Addressable multiregional and multifocal multiphoton microscopy based on a spatial light modulator. Journal of Biomedical Optics. 17 (3), 030505(2012).
- Mendoza-Yero, O., Carbonell-Leal, M., Mínguez-Vega, G., Lancis, J. Generation of multifocal irradiance patterns by using complex Fresnel holograms. Optics Letters. 43 (5), 1167-1170 (2018).
- Kuang, Z., et al. Diffractive Multi-beam Ultra-fast Laser Micro-processing Using a Spatial Light Modulator (Invited Paper). Chinese Journal of Lasers. 36 (12), 3093-3115 (2009).
- Kuang, Z., et al. High throughput diffractive multi-beam femtosecond laser processing using a spatial light modulator. Applied Surface Science. 255, 2284-2289 (2008).
Access restricted. Please log in or start a trial to view this content.
재인쇄 및 허가
JoVE'article의 텍스트 или 그림을 다시 사용하시려면 허가 살펴보기
허가 살펴보기더 많은 기사 탐색
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. 판권 소유