Axée sur la transformée de Fourier Diffraction Analysis of Live Caenorhabditis elegans

Résumé

Ce manuscrit décrit comment distinguer différents nématodes à l’aide de signatures de diffraction de champ lointain. Nous comparons la locomotion des 139 type sauvage et 108 « Roller » c. elegans en faisant la moyenne des fréquences associées à la signature de diffraction de Fraunhofer temporelle à un seul emplacement à l’aide d’un laser à onde continue.

Résumé

Ce manuscrit décrit comment classer les nématodes en utilisant des signatures temporelles diffraction de champ lointain. Un seul c. elegans est suspendu dans une colonne d’eau à l’intérieur d’une cupule optique. Un laser HeNe onde entretenue de 632 nm est dirigée dans la cuvette à l’aide des rétroviseurs frontaux de surface. Une grande distance d’au moins 20-30 cm que se sont rendu après que la lumière passe à travers la cuve assure un schéma de diffraction utile champ lointain (Fraunhofer). Les changements de schéma de diffraction en temps réel comme le nématode nage dans le faisceau laser. La photodiode est placée décentré dans le schéma de diffraction. Le signal de tension de la photodiode est observé en temps réel et enregistrées à l’aide d’un oscilloscope numérique. Ce processus est répété pour 139 type sauvage et 108 « roller » c. elegans. Type sauvage vers présentent un modèle d’oscillation rapide dans la solution. Les vers « roller » ont une mutation dans un élément clé de la cuticule qui gêne la locomotion lisse. Les intervalles de temps qui ne sont pas libres de saturation et l’inactivité sont ignorées. Il est possible de diviser chaque moyenne par son maximum pour comparer les intensités relatives. Le signal pour chaque ver est que transformée de Fourier transforme afin que le modèle de fréquence pour chaque ver émerge. Le signal pour chaque type de ver est en moyenne. Le spectre de Fourier en moyenne pour le type sauvage et le c. elegans « roller » est très différent et révèle que les formes ver dynamique des deux souches différentes de ver peuvent être distinguées à l’aide d’analyse de Fourier. Le spectre de Fourier de chacune des souches ver correspondre à un modèle approximatif à l’aide de deux formes différentes ver binaire qui correspondent aux moments locomotrices. L’enveloppe de la distribution de fréquence moyenne pour les vers de réels et modélisées confirme que le modèle corresponde aux données. Cette méthode peut servir de base à l’analyse de Fourier pour de nombreuses espèces microscopiques, comme chaque micro-organisme aura son spectre de Fourier unique.

Introduction

Cette méthode compare les spectres de fréquence expérimentale et modélisation de la locomotion des elegans de Caenorhabditis , avec deux souches très différents modes de locomotion. Les résultats montrent que le spectre de fréquence dépend de changements temporels comme le nématode nage dans une colonne d’eau afin que les images claires microscopiques ne sont pas nécessaires pour l’analyse. Cette méthode permet l’analyse quantitative en temps réel et fournit des informations complémentaires aux images/vidéos obtenues avec des microscopes traditionnels. Diffraction de Fraunhofer, également appelée diffraction de champ lointain, fournit la base pour l’obtention de diffraction live data^1,2. L’intensité lumineuse en un point unique dans le schéma de diffraction est le résultat de la superposition de lumière de chaque point dans l’esquisse de la nématode³. En conséquence, l’intensité lumineuse recueillie au fil du temps transporte des informations sur la locomotion du nématode. Analysant le signal dépendant du temps diffraction peut identifier le mouvement caractéristique du mutant correspondant depuis analysant toutes les fréquences impliquées dans la locomotion complète l’analyse vidéo traditionnel. Dans ce cas, les différences caractéristiques entre la locomotion du « rouleau » et de type sauvage c. elegans sont confirmées en comparant les spectres de fréquence des deux souches différentes du nématode.

Certaines caractéristiques précédentes ont été confirmés à l’aide d’analyse de la fréquence des signaux de diffraction telles que natation fréquences^2,4. Plus important encore, cette méthode peut être utilisée comme une méthode complémentaire à la microscopie traditionnelle à célébrer locomotion en temps réel sur un écran d’ordinateur, les données sont recueillies. Le spectre des fréquences de worms avec des patrons locomotrices distincts peut être quantifié en tenant compte de que la transformée de Fourier transforme signal signal de la diffraction.

La nature multidisciplinaire de la diffraction axée sur la transformée de Fourier dans cet ouvrage comporte les domaines de la biologie et la physique. Diffraction par sous échantillonnage a longtemps été utilisée pour étudier les structures cristallines en biologie⁵ et d’autres domaines. Dans cette expérience, cependant, suréchantillonnage^6,7 crée le modèle de champ lointain diffraction afin que l’organisme soit centrée dans le faisceau laser. Le suréchantillonnage est généralement utilisé pour lentille sans imagerie⁸ conjointement avec un algorithme d’extraction de phase qui reconstruit une image de l’objet original. Phase de récupération est difficile à réaliser lorsque les diffuseurs sont présents, comme c’est le cas avec un nématode. La signature temporelle de diffraction est suffisant pour évaluer des fréquences principales de la motion de ver. Cette méthode est moins taxer par le calcul et fournit un moyen optique pour quantifier la locomotion. Cette technique pourrait être facilement adaptée pour l’analyse des mutations ou des conditions environnementales qui altèrent le comportement.

Protocole

1. croissance de c. elegans et entretien

1. Pétri nématode Prepare.
   1. Remplir les boîtes de Pétri avec une solution d’agar et les laisser se solidifier, puis la souche semence avec une culture d’e. coli de la OP50 ^{9 , 10}.
2. Préparer une départ de la population de nématodes adultes sur chaque assiette en déplaçant plusieurs vers adultes à frais Pétri remplis de gélose avec un patch d’e. coli. Maintenir les cultures nématodes à 20 ° C dans un incubateur.
   NOTE : Souches de nématodes peuvent être obtenues depuis le centre de génomique de Caenorhabditis elegans. Pour cette étude, le type sauvage, N2, la souche et le OH7547 (otls199 [chat-2::GFP + rgel-1 (F25B3.3) :: dsRed + souche rol-6(su1006)]), qui présente un phénotype de rouleau, ont été utilisées.
3. Propager vers des cultures futures. Plat
   1. enlever le Petri contenant c. elegans et un habitat inutilisé Pétri de l’incubateur à température contrôlée. Placez-les sur la scène d’un microscope à dissection.
   2. Pour allumer le brûleur Bunsen et stériliser le pick nématode platine en plaçant le métal dans la flamme jusqu'à ce qu’il s’allume en rouge. Laisser ce choix pour refroidir à température ambiante. Ne pas fixés au rang ou laisser le choix entrent en contact avec des contaminants.
   3. Toucher doucement la pointe de ce choix pour sélectionner le bord du cercle des bactéries. Cette substance est collante et fera la cueillette des nématodes adultes individuels plus facile.
   4. Transférer jusqu'à 4 nématodes gravides à un nématode à croissance moyenne (NGM) remplis de gélose de Pétri et incuber à 20 ° C. Les vers pondront qui viendront à échéance dans quatre jours.
   5. Remettez les nématodes restants dans l’incubateur après le déplacement des nématodes adultes quatre.

2. La configuration optique ( Figure 1)

1. Secure l’hélium-néon laser près de l’arrière à gauche de l’établi optique et connectez-le à une source d’alimentation.
   Remarque : Le laser ' faisceau s doit remplir les conditions pour le suréchantillonnage. c. elegans sont d’environ 1 mm de long, donc le faisceau laser doit avoir un diamètre supérieur à 2 mm lors de l’incident sur le nématode, mais ne dépassant pas 5 mm pour que le patron de diffraction n’est pas difficile à localiser.
2. Placer un filtre de densité neutre entre le laser hélium-néon et l’échantillon telle que le faisceau laser traverse le filtre avant d’arriver à l’échantillon.
3. Direction d’aluminium surface avant deux à l’aide de miroirs, construire un périscope en obtenant le premier miroir après le filtre de densité neutre. Fixez le second miroir environ 10 cm sous le premier miroir pour permettre de diriger le faisceau laser et insérer la cuvette entre les miroirs. Aligner le faisceau laser et la cuvette afin que le faisceau laser se déplace verticalement dans la cupule.
   Remarque : La distance entre l’organisme de diffraction et la photodiode doit être beaucoup plus grande que l’organisme lui-même pour atteindre la diffraction de champ lointain. Dans cette expérience, la distance entre la cuvette et la photodiode est de 20 cm.
4. Fixer la photodiode directement en face du second miroir avec son capteur devant le miroir.
   Remarque : La cuve contenant le nématode sera placée entre les deux miroirs à l’aide de pinces de chimie. Voir les sections 4 et 5.
5. Placer une cuvette remplie d’eau sur le stand. Régler la hauteur du stand. Régler les hauteurs et des angles de miroir 1 et miroir 2 afin que le faisceau laser traverse la cupule vise près, mais pas directement à la photodiode.
6. Utilisez un niveau pour s’assurer que la forme des peuplements une surface nivelée pour la cuvette. Ajuster les rétroviseurs supplémentaires si nécessaire.
7. Connectez la photodiode à l’oscilloscope numérique à l’aide du câble USB fourni avec l’oscilloscope numérique. Connectez l’oscilloscope numérique à l’ordinateur qui sera utilisé pour enregistrer et sauvegarder les données.

3. Réglage de l’oscilloscope

1. en utilisant le logiciel de l’oscilloscope sur l’ordinateur, définissez la fréquence d’échantillonnage d’au moins 8 Hz à régler le cycle de l’écroulement du ver suffisamment.
   Remarque : La fréquence d’échantillonnage doit être deux fois plus élevé que des fréquences attendues s’emballer des espèces pour que le théorème de Nyquist ¹¹ est convaincu.

4. Préparation de la vis sans fin et la Cuvette pour la collecte de données

1. transférer quatre nématodes adultes à un frais NGM ¹⁰ remplis de gélose de Pétri à l’aide d’une pioche de fil de platine mince, aplati (voir la section 1.3).
2. Supprimer une cuvette en plastique jetable de son emballage, en prenant soin de seulement toucher la cuvette sur ses flancs striés.
3. Utiliser une micropipette à pipeter eau distillée dans la cuve jusqu'à ce que la cuve soit environ 80 % remplie avec de l’eau distillée.
   NOTE : Il faut seulement l’eau utilisation distillée ou ionisés tampons comme M9 ¹⁰ ou une solution saline tamponnée au phosphate (PBS) lorsque vous manipulez les nématodes, comme l’eau du robinet contient des composés de micro-organisme-tuer.
4. Placer la boîte de Pétri contenant c. elegans pour être utilisé sous une dissection étendue.
5. à l’aide de la pioche de platine, retirer une mature c. elegans de la boîte de Pétri et submerger le prélèvement dans la cupule, déplaçant le prélèvement dans les cercles si nécessaire pour déloger le nématode.
6. Pour éviter les bulles dans la cuve, remplir la cuve avec de l’eau jusqu'à ce qu’il est légèrement renflements sur la cuvette ' haut s. Remplir la cuvette ' cap s entièrement avec de l’eau puis mettez rapidement le chapeau sur la cuvette.
7. Utiliser un chiffon de nettoyage optique pour éliminer les gouttelettes d’eau versées plus et optique nettoyage papier pour nettoyer les petites gouttelettes restantes.

5. Acquisition des données en temps réel de Diffraction intensité changements

1. l’hélium-néon s’allume au laser et ajuster le réglage de la fréquence et/ou de la couleur afin qu’il produise un faisceau rouge. Tourner sur le capteur.
   Mise en garde : Utiliser un faisceau de faible consommation d’énergie à 632 nm, comme c. elegans éviter haute-fréquence (bleu) clair ¹².
2. Localiser le ver dans la cuve. Tenant la cuvette sur ses flancs striés, incliner délicatement la cuvette jusqu'à ce que le nématode est environ dans le centre de la portion de la cupule.
   NOTE : Secouant ou en inclinant la cupule violemment provoque le ver d’entrer en collision avec les parois de la cuve. Ceci peut endommager le nématode.
   1. Place la cuvette sur le support dans le système optique, le ver dans le laser de centrage ' s faisceau réfléchi de miroir 1 miroir 2. Veillez à éliminer les reflets.
3. Centre le ver dans le faisceau laser.
   1. Placer la photodiode dans le schéma de diffraction de sorte que l’emplacement de la photodiode et la centrale au maximum le patron de diffraction ne coïncident pas.
   2. Régler le filtre de densité neutre pour éviter la saturation de la photodiode. Rotation de la roue de filtre de densité neutre régule l’intensité lumineuse.
      1. Tournez la densité neutre filtrer pour qu’augmente la tension de sortie de la photodiode.
         Remarque : La tension de sortie est observée à l’aide du logiciel pour la photodiode numérique. La photodiode est saturée si la tension ne change pas. Dans ce cas, faire tourner le filtre de densité neutre jusqu'à ce que la tension diminue sans plafonne à une lecture minimale. S’assurer que le signal de tension ne pas aplatir à la lecture des crêtes, indiquant la saturation de la photodiode. Réduire l’intensité lumineuse en tournant la roue de filtre de densité neutre en cas de saturation.
   3. Une fois que le patron de diffraction mobiles est visibles, de recueillir des données avec la photodiode en cliquant sur le bouton Démarrer sur le logiciel contrôlant l’oscilloscope tout en surveillant le ver ' mouvement s. Continuer à prendre des mesures jusqu'à ce que le ver sort le faisceau laser et le diffraction modèle disparaît, qui prend habituellement environ 20 s. Processus
      1. arrêter la collecte de données en cliquant sur le bouton stop sur le logiciel de l’oscilloscope. Enregistrez chaque procès ' données au format .csv ou .txt.
4. Répétez les étapes 5.2-5.3 jusqu'à ce qu’au moins 50 ensembles de données ont été recueillies pour chaque phénotype. Huit à dix animaux utilisés par procès.
5. Si la cuvette est rayé dispose d’elle et le ver et répétez l’étape 4. Si le ver est bafouée dans le transfert, jetez-le et rincer la cuve avec de l’eau distillée avant de répéter l’étape 4 à l’aide de la même cuve.
6. Répéter l’étape 5 à l’aide de la OH7547 " rouleau " souche, en prenant soin d’étiqueter les données afin d’indiquer la souche ver.

6. Spectre de Fourier de données

1. Importer les données acquises dans un programme d’analyse de données capable d’effectuer des transformations de Fourier discrète ³.
2. Exécuter Fourier transforme sur chaque ensemble de données à l’aide de l’option de transform (FFT) transformée de Fourier rapide du logiciel.
3. Moyenne des fréquences d’après les résultats de la FFT pour chaque amplitude pour le type sauvage de N2 worms.
4. Répéter l’étape 6.3 à l’aide de la FFT de la OH7547 " rouleau " vers.

7. Modélisation de la spectre de Fourier

1. programme un modèle binaire du nématode locomotion (voir programme inclus dans les matériaux supplémentaires).
   Remarque : Ce modèle est une approximation, qui affiche d’abord les caractéristiques éminents du mouvement de la vis sans fin. Le modèle peut être affiné, car les résultats sont comparés avec worms réelles. Formes de ver sont approximatifs à l’aide de microscope images ¹³.
   1. Créer images séquentielles du modèle binaire se déplaçant à travers au moins deux cycles de ver ( Figure 2 a). Voir les vidéos dans les matériaux supplémentaires ; C ver video (CWorm.avi) et W ver video (WWorm.avi).
2. Produire des motifs séquentiels de diffraction. Voir les vidéos dans les matériaux supplémentaires. Vidéo C ver Diffraction (CWormDiff.avi) et W ver video (WWormDiff.avi).
   1. De Fourier chaque trame binaire de l’image de ver. Plus le remplissage du cadre autour de la vis sans fin, plus la résolution de l’image de diffraction sera.
      Remarque : La valeur absolue de chaque trame de transformée de Fourier est proportionnelle à la patron de diffraction correspondant ( Figure 2 b).
   2. Régler le contraste entre le patron de diffraction en mappant les intensités du patron de diffraction à une échelle logarithmique.
      NOTE : Appareils photo et les yeux ont tendance à fonctionner sur une échelle non linéaire. Une échelle logarithmique peut simuler comment un schéma de diffraction est généralement perçue par le œil humain.
3. Extraire le signal de diffraction modélisés.
   1. Choisir un emplacement excentré qui correspond à l’emplacement de la photodiode dans le schéma de diffraction.
   2. Ajouter les éléments de matrice voisines entourant l’emplacement de la photodiode pour simuler la taille de la photodiode. La taille de la photodiode est généralement 0,1 % de la structure modélisée par diffraction.
   3. Record et l’intrigue des signaux de la séquence de l’ampleur de la diffraction. Vérifier que le signal est physiquement raisonnable (c'est-à-dire, dans le cas de raclée périodique, le signal de la photodiode devrait être périodique ainsi).
4. Fourier transformer le signal de diffraction obtenu à 7.3 et comparer les résultats avec les données expérimentales.
5. Répéter pour diverses souches de ver et de comparer.

Résultats

Le montage expérimental optique illustré à la Figure 1 permet l’étude des micro-organismes sans être lié à un plan focal. Le signal de la volée de la photodiode peut être observé en temps réel sur l’écran de l’ordinateur, car les données sont collectées. Des tendances inhabituelles seront visibles immédiatement sans avoir à analyser une vidéo en détail.

Exemples de mouvement ver séquentielle modélisés et diffraction correspondante patrons sont indiquées à la Figure 2. Les patrons de diffraction modélisés qualitativement ressemblent à des modèles expérimentaux¹ et sont une première indication que les simulations du modèle avec succès le nématode.

Une signature de diffraction temporelle échantillon des deux types c. elegans a étudié ici est illustrée à la Figure 3. Il peut être vu qualitativement que chaque nématode fustige à amplitudes et des taux différents. Certaines des différences peuvent être quantifié par le biais de courbe comme cela a été fait dans une précédente publication¹. La transformation de Fourier discrète, cependant, révèle plus de détails au sujet de fréquences intégrés :

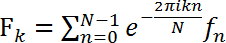, (1)

où F_k est la transformée de Fourier numérique (FT) et f_n est le signal dépendant du temps diffraction brut avec le temps discret variable n et la variable de fréquence discrète k. N est le nombre total de points de données. La transformée de Fourier numérique moyenne permet le nématode d’être identifiés par l’amplitude de son spectre de fréquence de diffraction (Figure 4). Le spectre de type sauvage est dominé par des fréquences plus basses que le spectre de mouvement de rouleau.

Un modèle qui se rapproche du type sauvage contre les notes de c. elegans rouleau type sauvage tend à thrash dans un mouvement ondulatoire de (forme W ou S) (Figure 2 a), tandis que le galet tend à favoriser un côté qui ressemble à peu près à une forme oscillante de C ( Figure 5). Cela offre une explication pour les différents spectres. Le rouleau constitueront surtout un C sur le côté tandis que l’oscillation de W peut être considérée comme deux opposés C des requêtes. Pour cette raison, la motion de W est plus complexe, révélant plus secondaires basses fréquences que la motion C. Ce résultat est confirmé par le modèle de calcul. La forme de W a une densité de fréquence beaucoup plus élevée que la forme C (Figure 6). Ceci est confirmé dans la FFT en Figure 4 où les fréquences de rouleau sont plus concentrés bien que pas totalement discret. Les statistiques du rouleau sont faussés car le rouleau peut revenir à la locomotion type sauvage temporairement.

Les spectres de puissance lissée de type rouleau c. elegans montre un pic large à ~1.5 Hz, tandis que le type sauvage de natation c. elegans montre un spectre multimodal (y compris pics à ~1.0 Hz et 1,75 Hz). La photodiode (pp) a une taille finie s’étendant sur plusieurs éléments de la matrice. Éléments de la matrice individuels ou des points sur le patron de diffraction varient en intensité puisque les interférences constructives et destructives varient ; Néanmoins, la fréquence à laquelle les intensités varient est les mêmes pour tous les éléments de la matrice, comme peut être vu à la Figure 7. Compte tenu de la dérivée temporelle EQ 1, on voit que les fluctuations de fréquence ne dépendent pas de la matrice de phase mais seulement sur les fluctuations de l’objet original :

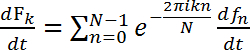, (2).

Comme le parti démocrate s’étend sur plusieurs éléments de la matrice, les emplacements de pointe moyenne et un profil de fréquence cohérente. Quelques variations peuvent être attendues et peuvent donner des indices sur l’orientation du ver. La distribution des fréquences va changer comme l’allure des changements ver. Le modèle actuel est un modèle simple qui ne permet pour l’évaluation des emplacements de pointe plutôt que les hauteurs relatives des pics. Différents modes de locomotion en moyenne à des endroits différents pic.

Figure 1. Montage expérimental. Les voyages de faisceau laser de faible puissance à travers le filtre de densité neutre, se traduit par miroir M1 vers le bas à travers la cuve contenant le ver sur miroir M2 et voyages vers la photodiode. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

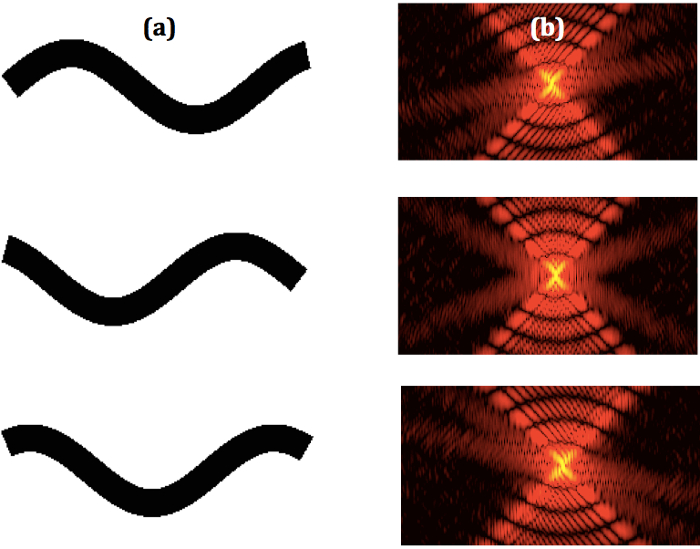
Figure 2. Ver séquentielle des formes et des patrons de Diffraction correspondant. (a) certains sélectionnez séquence d’images binaires de nématodes de forme modélisées W et les modèles de diffraction séquentielle correspondants (b). S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

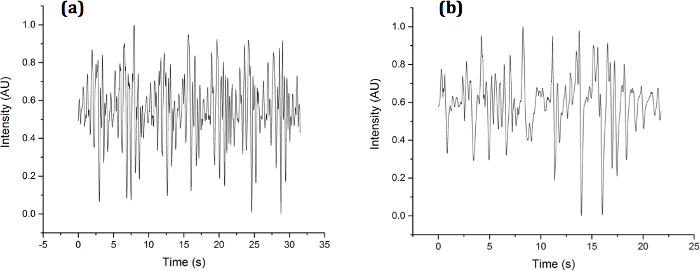
Figure 3. Signatures de Diffraction échantillon expérimental. Diffraction des signatures récoltées pour (a) OH7547 « roller » et (b) N2 type sauvage c. elegans en utilisant une photodiode unique dans le modèle de diffraction. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

Figure 4. Expérimentales en moyenne des spectres de puissance de rouleau et de Type sauvage Fraunhofer Diffraction série. Le show de spectres les fréquences présentent en moyenne de Fourier de la série temporelle enregistré avec la photodiode. Un filtre gaussien de déviation standard 0,075 Hz, 3 écarts-types, ils sont tronqué est utilisé pour le lissage. Notez le pic spectral large à ~1.5 Hz dans le spectre de rouleau lissé, comparé avec le spectre de multimodal lissée sauvage (y compris les pics à ~1.0 et 1.75 Hz). S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

Figure 5. Diffraction Formation Illustration. Patrons de diffraction peuvent être modélisées par la pensée de chaque segment de ligne qu’une infime ligne droite (à gauche). La superposition de ces lignes (à droite) illustre la construction de diffraction de champ lointain générée par un C en forme de nématode. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

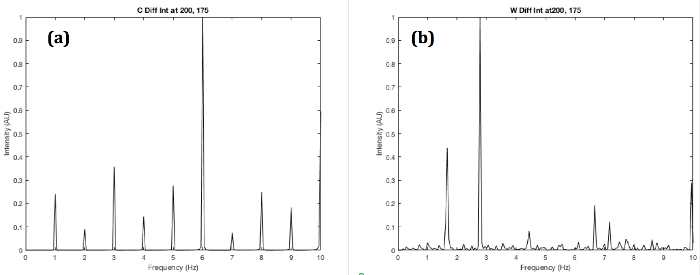
Figure 6. Simulation des spectres de puissance de rouleau et de Type sauvage Fraunhofer Diffraction série. (a) C (b) et la forme W forme Pandore avec la photodiode centré sur les éléments de matrice 200 (vertical) et 175 (horizontal). La forme W montre une densité plus élevée des fréquences en raison de la locomotion plus complexe. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

Figure 7. Simulation des spectres de puissance de rouleau et de Type sauvage Diffraction de Fraunhofer série à Photodiode différents endroits. (a) W forme ver et le ver de forme (b), C pour les éléments de la matrice unique à divers endroits simulant divers endroits de la photodiode. Hauteurs des pics varient à différents endroits ; Cependant, lieux de pic reste les mêmes pour des formes spécifiques. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

Discussion

Y compris les étendues de données à l’inactivité seront fausser les résultats, puisque les fréquences les plus basses artificielles seront moyennés dans les résultats. Saturer la photodiode se distingue par des pics de plats ou pics « couper » dans les données brutes. Divisant chaque ensemble de données brute par intensités maximales aidera avec comptabilisation des variations dans l’intensité du laser.

Les fréquences de pointe sont un indicateur de l’ensemble de sa volée de fréquence ; Cependant, mouvement compliqué cause du brouillage à des fréquences de battements dans le schéma de diffraction et doivent être examinées avec soin.

Cette méthode peut être utilisée pour étudier la locomotion des autres nématodes. L’environnement peut être modifié sur un autre support. Longueurs d’onde peuvent être changées ainsi. Travaillant dans le domaine du visible du spectre électromagnétique, c’est plus facile et plus sûre.

Un modèle plus perfectionné simulera les spectres de diffraction plus réaliste à l’avenir. Un futur modèle peut inclure un ver qui peut changer les orientations, qui n’affecterait pas les lieux de la fréquence, mais les hauteurs relatives des pics. Un modèle plus réaliste permettrait une répartition probabiliste des fréquences de volée, ce qui élargirait les pics comme dans les données expérimentales. Une répartition en fréquences expliquerait les variations dans les fréquences de s’emballer.

La forme actuelle de ver est brute, en particulier dans la région de la tête et la queue, qui devrait être plus effilée que dans le modèle actuel. Il peut être intéressant d’effectuer une analyse détaillée de la série temporelle du signal car il pourrait donner des indices sur la complexité de la locomotion chez les mutants différents.

Il est utile d’examiner la faisabilité d’étendre cette technique en caractérisant les nématodes multiples simultanément. Cette méthode doit être comprise comme une méthode complémentaire aux méthodes existantes à l’aide de microscopes traditionnels. Cette méthode a un avantage en n’exigeant ne pas de microscope lors de l’acquisition des données afin que le ver peut se déplacer hors du plan focal. Les spectres de fréquence moyenne montrent des différences évidentes dans la motion de ver et peuvent être quantifiés par les pics de fréquence courante, qui est une nouvelle méthode pour quantifier la locomotion de ver. Analyse des données des signatures de diffraction est en développement et j’espère conduira à un processus automatisé d’identification des multiples des mutants et des individus.

matériels

Name	Company	Catalog Number	Comments
Tunable Helium-Neon laser	Research Electro-Optics	30602	Four wavelengths can be selected between 543 nm and 633 nm.
2 Front Surface Aluminum Mirrors	Thorlabs	PF10-03-F01
Photodiode: SI Amplified Detector	Thorlabs	PDA 100A
Quartz Cuvette	Starna Cells	21/G/5	Plastic cells may be used as well.
MatLab (Software)	MathWorks	R2016b (9.1.0.441655)	Use the fft command to simulate diffraction
Excel	Microsoft	14.7.1	Used for data analysis of Figure 4
Caenorhabditis elegans Roller	University of Minnesota Caenorhabditis elegans Center (CGC)	Strain: OH7547 Genotype: otIs199.	https://cbs.umn.edu/cgc/home
Caenorhabditis elegans Wild Type	University of Minnesota Caenorhabditis elegans Center (CGC)	Strain:N2 Genotype: C. elegans wild isolate	https://cbs.umn.edu/cgc/home