Réacteur catalytique : Hydrogénation de l'éthylène
Vue d'ensemble
Source : Kerry M. Dooley et Michael g. Benton, département de génie chimique, Louisiana State University, Baton Rouge, Louisiane
L’hydrogénation de l’éthylène (C2H4) en éthane (C2H6) a souvent été étudiée comme une réaction de réduction de modèle pour la caractérisation de nouveaux catalyseurs métalliques. 1-2 nickel pris en charge n’est pas le catalyseur métallique plus actif pour cette réaction, il est suffisamment actif pour que la réaction peut avoir lieu à < 200 ° C.
La réaction implique typiquement hydrogène adsorbé, dissocié (H2) réagit avec l’éthylène adsorbé. En d’autres termes, les deux atomes d’hydrogène et d’éthylène forme de molécules liens avec un site de métal (ici noté « S »). La liaison forte d’éthylène avec S affaiblit la double liaison suffisamment pour permettre à des atomes d’hydrogène ajouter à l’éthylène, formant l’éthane, qui n’est pas adsorbé.
Le but de cette expérience est, tout d’abord, pour convertir des mesures de composition brute pour limiter les conversions de fractions de réactif. 3 ces conversions puis utilisable dans un réacteur d’écoulement (PFR) pour ajuster les données à un modèle standard Loi de puissance cinétique par la méthode « intégrale ». 3 une comparaison entre les ordres expérimentales de réaction de l’éthylène et de l’hydrogène avec les ordres théoriques révèle dans ce cas que la réaction est cinétiquement contrôlée plutôt que de la masse-transfert contrôlé.
Principles
Un mécanisme pour la réaction (laisser A = éthylène, E = éthane et S = un site métal) peut être écrite comme :2
A + S 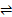 (1)
(1)
H2 + 2 S 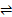 HS + HS (2)
HS + HS (2)
AS + HS 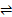 AHS + S (3)
AHS + S (3)
Papa + HS 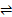 E + S + S (4)
E + S + S (4)
Si nous supposons que la troisième réaction est l’étape cinétiquement limitante, et que le montant total des sites de S est constant (So), nous pouvons utiliser un bilan de masse approximative :
(So) ~ (S) + (AS) + (HS) (5)
et l’hypothèse de quasi-équilibre sur mesures (1) - (2) pour obtenir une expression cinétique théorique :
r = k (H2)1/2 (A) (So)2 [1 + K1 (A) + K21/2 (H2)1/2]-2 (6)
où k est une constante de vitesse, K est une constante d’équilibre, « 1 » représente la première réaction, « 2 » pour la seconde réaction et H2, (A) et (So) sont les concentrations de chacun des composants. Notez que, dans l’approximatif, nous partons du principe de bilan massique que (S), (HS) et (AS) >> (AHS). Notez également que (So) est une constante tant que le nombre total de sites métalliques reste le même. Lorsque le nombre de sites métalliques diminue en fonction du temps, nous disons que le catalyseur « désactive » ; quand il augmente, le catalyseur « active ». Dans cette réaction, désactivation peut être causée par une réaction secondaire avec cette stoechiométrie :
un C2H4  (CH)2 a + H2 (7)
(CH)2 a + H2 (7)
Le polymère produit (CH)2 a (« coke ») est trop lourd (« a » est grande) de désorption du métal et donc ces sites de métal et sont effectivement retirés le catalyts. 4 Toutefois, des conditions de réaction ultérieure peuvent provoquer le coke à se décomposer, ainsi « réactiver » le catalyseur.
Pour ces cinétique, il est évident que, pour les faibles concentrations de l’éthylène, le taux est du premier ordre en éthylène, alors que pour des concentrations élevées d’éthylène, la vitesse de réaction est ordre-1. Les valeurs comparables pour l’ordre de l’hydrogène sont 0,5 à -0,5. Taux des expressions de ce type (aussi commun dans les réactions catalysées par les enzymes) sont appelées « Langmuir-Hinshelwood ». L’équilibre constante K1 étant dépendante de la température, cette expression cinétique nous dit que l’ordre m de l’éthylène dans une expression de la « Loi de puissance » cinétique du type :
r = k (A)m (H2)n (8)
va changer avec la température. Taux de la plupart des expressions en fonction des données expérimentales sont du type « power-law », comme on le voit dans les manuels standards cinétique chimique. 5
Ci-dessous un schéma simplifié du système réacteur (Fig. 1). Bon nombre des soupapes et des composants sont étiquetés sur le réacteur. Le réacteur est un tube d’acier contenu dans un sandbath. Le sandbath est fluidisé avec de l’air et chauffé par le chauffage de résistance aux métaux. Une grande quantité de chaleur peut être transférée rapidement vers le réacteur de l’usine pilote.
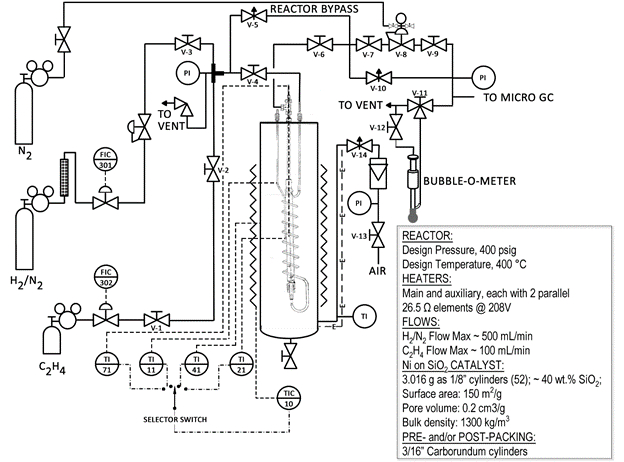
Figure 1 : Schéma du système de réacteur catalytique
Des précautions ont été prises pour ce faire un système sécurisé. Il y a de soupapes sur le système, un arrêt de la haute température, et seulement les hydrogène dilué (voir fiche technique sur le cylindre) sont utilisé. Cependant, avec tous les systèmes faisant réagir, strict respect des procédures de sécurité est nécessaire. La limite inférieure d’explosion d’hydrogène dans l’air est de 4,0 % en volume. 6 c’est pourquoi il est important de s’assurer que le réacteur ne coule pas hydrogène dans la sandbath environnante. Un détecteur de fuite de gaz Combustible CGD900 est disponible à cet effet.
Le catalyseur utilisé dans cette démonstration (2,0 g) utilise nickel que le composant actif mais est environ 40 wt % de silice (SiO2). La silice est appelée un « soutien » pour le nickel, et son but est d’offrir une grande surface pour le nickel à couvrir. Un matériau inerte, le carbure de silicium (SiC), est utilisé pour remplir le reste du réacteur. Le catalyseur a superficie = 150 m2/g, volume de pore = 0,2 cm3/g et une masse volumique de ~ 1300 kg/m3.
Le réacteur idéal plus proche d’un réacteur catalytique de garnissage est un PFR. Analyse de réacteur non-idéal déborde le cadre de cette expérience. Le bilan massique de PFR avec poids de catalyseur comme variable indépendante et conversion fractionnaire comme variable dépendante devient :
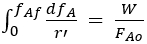 (9)
(9)
où fbis est la conversion fractionnaire du réactif limitant, « f » signifie des conditions finale (sortie), W est le poids de catalyseur, FAo l’alimentation débit molaire de A et r' est l’expression de taux sur une base par wt. Comment mettre des r' en termes de fA seulement d’un gaz idéal est couvert dans l’une des références standard cinétique. 3 Notez qu’il y aura deux catégories de données, une classe avec la limitation de l’éthylène et l’autre avec la limitation de l’hydrogène, mais il ne peut exister qu’une seule expression de taux commun. On trouvera la conversion fractionnaire en analysant les flux et produit des gaz avec un chromatographe en phase gazeuse. Par le biais de clôture du bilan de masse, la vitesse de la réaction présents et par rapport à l’énergie d’activation nominal pour ce type de réaction catalytique. Il permet également de comparer les ordres de la réaction.
Procédure
Le système est contrôlé par un système de contrôle distribué commerciale ; Il n’y a qu’une seule interface opérateur.
1. démarrage du réacteur
- Pour démarrer la vue historique de processus en temps réel, accédez à démarrer > DeltaV > opérateur > processus histoire vue et puis ouvrez CATUnitOverview. Tableau des échelles peuvent être compressés ou élargis en cliquant sur ces boutons dans la barre de menu. Procédures de télécharger les données du système de contrôle dans une feuille de calcul Excel sont disponibles sur l’ordinateur.
- Assurez-vous que le sandbath de l’air est sur. Le rotamètre devrait lire ≈5 ou plus et être maintenu constant d’une exécution à l’exécution pour assurer le chauffage uniforme.
- Permettent une alimentation principale pour le chauffage de sandbath en appuyant sur le bouton Démarrer de couleur noire sur le panneau de l’unité de la CAT.
- Contrôleur de température (TIC-10, pour le sandbath) la valeur consigne initiale désirée, mode auto. Pour utiliser le chauffage au début de l’expérience rapide, se reporter à l’annexe A.
- Les températures peuvent être surveillés sur le graphique. Le taux de débit de l’effluent du réacteur doit être vérifié périodiquement. Si problèmes, tels que la perte de température de coulée ou emballement se développer, coupez les deux flux de réactifs à l’aide de vannes d’arrêt approprié et tourner tous les appareils hors tension. Laisser un sandbath air.
2. réglage des débits
La valeur des débits avant chauffage. Étalonnages pour les régulateurs de deux débit - FIC-301 pour le mélange hydrogène-azote - et FIC-302 pour l’éthylène seront fournis.
- La valeur numérique sur l’interface qui indique si l’ordinateur ou le panneau sera utilisé à 1 pour indiquer l’utilisation de l’ordinateur.
- Bloquer la conduite de prélèvement de GC.
- Déterminer le débit volumétrique en chronométrant la vitesse de montée d’une bulle unique entre deux volumes dans un compteur de bulles. Un compteur de bulles est un buret verre graduée volumes. Assurez-vous que la ligne d’échantillonnage GC est bloquée lorsque le compteur de bulles est activement utilisé pour mesurer des flux (étalonnage, vérification des taux de débit de sortie).
- Prendre au moins un échantillon de l’aliment par le by-pass (un échantillon témoin) pour vérifier sa composition. C’est OK pour modifier les débits à la volée sans contournement du réacteur. Changer les débits aussi changements les concentrations relatives de l’aliment (la pression est constante), débits tant devra être changé souvent.
- Débloquer la conduite de prélèvement de GC et couler les réactifs par le réacteur bypass et à l’orifice du GC.
- Un chromatographe en phase gazeuse permet d’analyser la composition des gaz produits. Instructions complémentaires figurent à l’appendice B sur comment faire fonctionner le GC et déterminer la composition.
3. arrêt du réacteur
- Arrêt alimentation jusqu’au radiateur sandbath en poussant le rouge EMERG. Interrupteur d’arrêt sur le panneau de l’unité de la CAT.
- TIC-10 place dans la mode homme et ensemble la sortie à 0 %. Groupes auxiliaires de puissance (si active) de la valeur à 0 %.
- Débit d’éthylène réglée à 0 % en mettant le contrôleur chez l’homme et de réglage de la sortie à 0 %.
- Fermer les deux vannes de sectionnement de l’éthylène avant le mixage té et d’arrêt le robinet de gaz.
- Laissez le courant d’hydrogène/azote pendant environ 2 min avant de s’éteindre ; cela prolongera la vie du catalyseur.
- Bloquer les deux vannes avant le mixage tee. Puis fermer le robinet principal pour le mélange hydrogène/azote.
- Laisser l’air à lit fluidisé.
Résultats
Régression non linéaire pour obtenir les meilleures estimations (en utilisant NQE. 8-9) de la réaction ordonne m et n et la constante de vitesse k, peuvent être fastidieux. Un tel algorithme de solution nécessite une intégration numérique par point de données par itération de m et n, conduisant à des milliers d’intégrations numériques. Une autre technique qui est presque aussi bon, mais beaucoup moins coûteuse, consiste à formuler des paires du procès de m, n, basée sur la structure de l’équation 6. Toutes les valeurs dans la plage des ordres théoriques est certainement possible. Puis définir une fonction objective du type :
 (10)
(10)
Cette fonction objective pour chaque m, paire n peut être calculée, et le meilleur ajustement déterminé à l’aide de son minimum ou près-minimum ainsi que d’autres critères de forme standard, tels que le caractère aléatoire des erreurs dans EQ. 10 en fonction des pressions partielles. Notez également que l’équation 9 prédit qu’un complot de la gauche intégrale (appelons-le « Y ») vs 1/FAo (appelons-le « X ») doit être linéaire à la m optimale, n. vérification du degré de linéarité et le caractère aléatoire des erreurs de cette formulation est aussi une méthode valable pour dissuader qualité de l’ajustement de la mine.
Certaines données prises à P = 1 atm, T = 80° C, P,C2H4 = 0,17-0,42 atm, PH2 = 0,23-0,33 atm (azote comme diluant) ont été analysées comme décrit ci-dessus. Le tracé linéaire de la cinétique « la mieux adaptée » est illustré à la Figure 2. Plusieurs autre m, n paires également examinées de la même façon et donne des ajustements linéaires les plus pauvres. Le meilleur ajustement des valeurs de m et n indiquent que l’éthylène est faiblement adsorbés sur le catalyseur de nickel (aucune inhibition dans le dénominateur de l’équation 6), tandis que l’hydrogène est fortement adsorbé (l’ordonnance négative indique l’inhibition). Pour des réactions catalytiques plus, trop fort qu'une adsorption est tout aussi mauvaise que trop faible une adsorption, bien que « trop fort » se reflète dans un ordre de réaction négative, tandis que « trop faible » transparaît dans les conversions faibles et un faible taux de constante k.
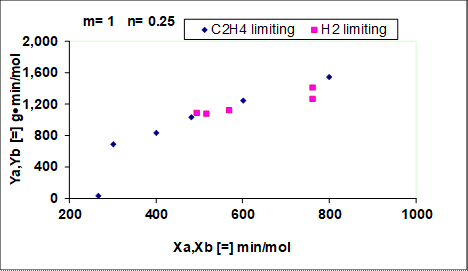
Figure 2 . Analyse de la cinétique de l’hydrogénation de l’éthylène à 80° C, 1 atm pour 60 % en poids de catalyseur de Ni. Le « a » désigne données où C2H4 est le réactif limitant, tandis que « b » désigne H2 comme le réactif limitant.
Les deux meilleures valeurs fit de m et n sont dans la plage d’attentes basées sur l’équation (6). La valeur de « m » est à son maximum, donc la réaction n’est pas contrôlée par la diffusion. Pour une réaction contrôlée par la diffusion à la fois « m » et « n » serait proche de zéro. Les ordres expérimentales peuvent parfois répondre à la question du point de vue cinétique par opposition aux contrôlée par la diffusion, mais si les deux ordres étaient proche de zéro, rien ne pouvait être prouvé, car zéro est situé dans la gamme de possibilité de commandes basé sur l’équation (6). Une preuve des déclarations ci-dessus déborde le cadre de cette expérience.
Applications et Résumé
La méthode décrite ici est appelée la « méthode intégrale » dans la plupart des livres sur le design cinétique et le réacteur. 3 s’il est mathématiquement beaucoup plus difficile à appliquer que les méthodes différentielles, il est également mieux adaptée pour analyser les types de données qui sont faciles à obtenir dans la plupart des systèmes de réacteur pilote, où les pressions partielles des réactifs et des produits et conversions de fractions peuvent varier sur une vaste gamme. Parce que nous ne comptons pas sur les réacteurs biologiques séquentiels ou conversions peu réactif, cesdonnées « intégrante » sont également plus précises et pertinentes pour scaleup. La première partie de la méthode doit convertir les données brutes des mesures de débit et de la composition en conversion fractionnaire vs espace temps (la partie droite de l’équation 9 s’appelle souvent l’espace temps). L’étape suivante consiste à postuler les ordres de réaction raisonnable pour les réactifs (et parfois les produits) qui influent sur le taux. L’étape finale consiste à comparer des ensembles autant de commandes que possible en utilisant l’équation (10), ou la relation de linéarité dans l’équation (9) et choisir l’ensemble qui donne le meilleur ajustement à toutes les données.
Presque n’importe quel catalyseur métallique supporté peut catalyser l’hydrogénation de l’éthylène sur une plage de température, et l’activité du catalyseur, la sélectivité (éthane) et la stabilité (résistance de cokéfaction) sont des descripteurs importants d’utilitaire de catalyseur métallique potentiels. Les ordres de cinétiques de la réaction sont également importants descripteurs. Ils indiquent la force relative d’adsorption d’un hydrocarbure par rapport à l’hydrogène, et si les taux du catalyseur peuvent être restreint par diffusion réactif ou produit (dans ce cas, sont trouvent les ordres près de zéro). Les ordres peuvent également suggérer si les hypothèses faites en dérivant l’équation 6 (par exemple, une seule étape cinétiquement limitante qui est la réaction de surface) sont encore corrects en premier lieu. Habituellement, connaissant l’expression de vitesse expérimentale ne suffit pas à déterminer le mécanisme exact en soi, mais si l’expression de vitesse expérimentale est incompatible avec un mécanisme réactionnel proposé, puis celui-ci est certainement incorrecte. Dans l’exemple donné ici, les cinétiques observées sont compatibles avec le mécanisme proposé et l’étape cinétiquement limitante, certaine créance au mécanisme de prêt.
Avec seulement légère adaptation, les « méthodes intégrante » décrites ici ont servi à déterminer les expressions de taux pour les nombreuses réactions catalytiques industrielles importantes. Ces expressions de taux ont ensuite été utilisées pour intensifier ces processus à des échelles de tonnage. Quelques exemples bien connus incluent le reformage du méthane à générer H2, l’oxydation du o-xylène à l’anhydride phtalique et la synthèse de l’ammoniac. 6 dans ce cas, les expressions de taux pour des centaines de catalyseurs candidat pourraient être calculées, souvent à plusieurs températures.
En ce qui concerne les réactions catalytiques métaux pris en charge, ils constituent certaines des réactions catalytiques industrielles plus importantes, y compris les échappements automobiles catalyse (une combinaison de l’oxydation du monoxyde de carbone, l’oxydation d’hydrocarbures imbrûlés et d’oxyde nitrique réduction), la réforme des linéaires aux hydrocarbures ramifiés pour augmenter l’indice d’octane de divers carburants et reformage à la vapeur. Pour le premier d'entre eux le métal actif est généralement un alliage de platine-palladium, pour la deuxième que c’est platine ou un alliage de platine tels que Palladium-rhénium, et pour la troisième, c’est nickel. 7 autres métaux comme le cuivre, argent, or et rhodium également trouve application, soit par eux-mêmes, soit comme alliages avec d’autres métaux.
Annexe A – Instructions de chauffage d’appoint
Pour un chauffage rapide, allumez le chauffage d’appoint (sortie ≤ 90 %), mais n’oubliez pas d’éteindre quand la peau ou la température de la paroi externe se rapproche de la température du réacteur souhaitée ; le chauffage d’appoint n’est pas contrôlé en ce moment et refroidissement (≈10 ° C/h) prend beaucoup plu de de chauffage. La température du réacteur peut accusent un retard significativement la température du chauffe-eau. Le thermocouple de peau peut être sélectionné comme l’entrée de TIC-10. La température la plus élevée pour être utilisé dans toute expérience est de 200° C. Un voyant d’avertissement de « Critique » avertit l’utilisateur à des températures élevées. Le système de contrôle surveille les températures le sandbath et le réacteur et les deux sont programmés pour l’alarme et mettre hors tension les appareils de chauffage quand il est trop élevé.
Annexe B – chromatographe, mode d’emploi
Le MicroGC est contrôlé par ordinateur. La méthode GC par défaut est « refroidissement-1 ». Pour les expériences, la méthode « PH-CAT4 » load. Cliquez sur contrôle → méthode de téléchargement. Afficher l’état de l’Instrument en cliquant sur commande → statut d’Instrument. Une course ne peut être effectuée jusqu'à ce que tous les paramètres dans l’état de l’Instrument sont près de leurs points de réglage.
Lorsque vous êtes prêt à effectuer une course, cliquez sur contrôle → Single Run. Un menu contextuel vous invite à entrer un ID d’échantillon, le fichier de données et le nom de résultat. « Fichier de données », cliquez sur la flèche vers la droite et sélectionnez la Date et l’heure. Après cela, l’écran sera sur le terrain, et la date et l’heure seront attachés aux noms de fichier. Pour les « Résultats », cliquez sur la flèche vers la droite échant., puis répétez la sélection de Date et d’heure, puis sélectionnez Répéter la sélection numéro d’incrémentation. Revenir sur le terrain et insérer un seul espace vide entre la première et la deuxième question et le deuxième et le troisième élément. « Nombre de répétitions entrer le nombre séquentiel analyses répétées désiré. Maintenant cliquez sur « Démarrer ». Les parcelles direct pour les deux canaux A et B seront affiché, indiquant les chromatogrammes telles qu’elles sont créées. H2 et N2 sont détectés sur le canal A, tandis que H2, CH4, C2H4et C2H6 sont détectés sur canal B. actuellement, cependant, la méthode a seulement été calibrée pour l’éthylène et de l’éthane. Lorsque toutes les répétitions sont terminées, ne pas enregistrer la méthode. La fenêtre de la séquence de résultat s’ouvre, permettant l’accès aux résultats.
Pour afficher les résultats, sélectionnez la fenêtre de la séquence de résultat, faites un clic droit (par exemple) la première cellule numéro exécution, choisissez sélectionner enregistrement. Sur le menu principal sélectionnez rapports → affichage → zone %. Un rapport avec les composés connus sautera vers le haut.
Le GC enregistrera en % de la superficie. Pour le calcul de conversion (A = % de zone) :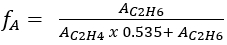 (11)
(11)
Il est également possible de calculer la conversion en mesurant le débit de produit avec le compteur de bulles, et cela peut servir à vérifier sur les résultats de GC. En supposant un gaz parfait et aucune réaction autre que de l’hydrogénation de l’éthylène, l’équation suivante peut être calculée en utilisant une table stoechiométrique :3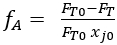 (12)
(12)
Où FT0 est le débit volumétrique total des aliments pour animaux, FT est le débit volumétrique total du flux de produit, tel que mesuré par le compteur de bulles, et 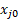 est la fraction mol ou le volume de celui qui est le réactif limitant.
est la fraction mol ou le volume de celui qui est le réactif limitant.
References
- O. Beeck, Discuss. Faraday Soc.8, 118 (1950).
- J.B. Butt, AIChE J22, 1 (1976).
- H.S. Fogler, "Elements of Chemical Reaction Engineering," 4th Ed., Prentice-Hall, Upper Saddle River, NJ, 2006, Ch. 2-4; O. Levenspiel, "Chemical Reaction Engineering," 3rd Ed., John Wiley, New York, 1999, Ch. 4-6; C.G. Hill, Jr. and T.W. Root, "Introduction to Chemical Engineering Kinetics and Reactor Design," 2nd Ed., John Wiley, New York, 2014, Ch. 8.
- B. Peri, Discuss. Faraday Soc., 41, 121 (1966).
- Basic chemical kinetics - Fogler, Ch. 3, Levenspiel, Ch. 2, Hill and Root, Ch. 3.
- N. Bartknecht, "Explosions: Course, Prevention, Protection", Springer-Verlag, 1981.
- G.F. Froment, K.B. Bischoff and J. De Wilde, "Chemical Reactor Analysis and Design," 3rd Ed., John Wiley, Hoboken, Ch. 11.
- J.R.H. Ross, "Heterogeneous Catalysis: Fundamentals and Applications," Elsevier, Amsterdam, 2012, Ch. 8.
Passer à...
Vidéos de cette collection:

Now Playing
Réacteur catalytique : Hydrogénation de l'éthylène
Chemical Engineering
30.4K Vues

Test de l'efficacité du transfert de chaleur d'un échangeur de chaleur à ailettes et à tubes
Chemical Engineering
17.9K Vues

Utilisation d'une étuve à plateaux pour étudier le transfert de chaleur par convection et par conduction
Chemical Engineering
43.9K Vues

Viscosité des solutions de propylène glycol
Chemical Engineering
32.8K Vues

Porosimétrie d'une poudre de silice et d'alumine
Chemical Engineering
9.6K Vues

Démonstration de la loi de puissance grâce à l'extrusion
Chemical Engineering
10.0K Vues

Absorbeur de gaz
Chemical Engineering
36.7K Vues

Équilibre vapeur-liquide
Chemical Engineering
89.0K Vues

L'effet du taux de reflux sur l'efficacité de la distillation en plateaux
Chemical Engineering
77.7K Vues

Efficacité de l'extraction liquide-liquide
Chemical Engineering
48.5K Vues

Réacteur à phase liquide : Inversion du saccharose
Chemical Engineering
9.7K Vues

Cristallisation de l'acide salicylique par modification chimique
Chemical Engineering
24.2K Vues

Écoulement monophasique et diphasique dans une colonne à garnissage
Chemical Engineering
18.9K Vues

Cinétique de la polymérisation par addition
Chemical Engineering
16.1K Vues

Évaluation du transfert de chaleur d'un Spin-and-Chill
Chemical Engineering
7.4K Vues