Source: David Guo, College of Engineering, Technology, and Aeronautics (CETA), Southern New Hampshire University (SNHU), Manchester, New Hampshire

A Pitot-static tube is widely used for measuring unknown speeds in air flow, for example, it is used to measure airplane airspeed. By Bernoulli's principle, airspeed is directly related to variations in pressure. Therefore, the Pitot-static tube senses the stagnation pressure and static pressure. It is connected to a manometer or pressure transducer to obtain pressure readings, which allows airspeed prediction.

In this experiment, a wind tunnel is utilized to generate certain airspeeds, which is compared against Pitot-static tube predictions. The sensitivity of the Pitot-static tube due to misalignment with respect to flow direction is also investigated. This experiment will demonstrate how air flow speed is measured using a Pitot-static tube. The goal will be to predict the air flow speed based on the pressure measurements obtained.

Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure and vice versa. Specifically, if the speed of a fluid decreases to zero, then the pressure of the fluid will increase to its maximum. This is known as the stagnation pressure or total pressure. One special form of Bernoulli's equation is as follows:

Stagnation pressure = static pressure + dynamic pressure

where the stagnation pressure, P_o, is the pressure if the flow speed is reduced to zero isentropically, the static pressure, P_s, is the pressure the surrounding fluid is exerting on a given point, and the dynamic pressure, P_d, also called ram pressure, is directly related to the fluid density, ρ, and flow speed, V, for a given point. This equation only applies to incompressible flow, such as liquid flow and low-speed air flow (generally less than 100 m/s).

From the above equation, we can express flow speed, V, in terms of pressure differential and fluid density as:

In the 18^th century, French engineer Henri Pitot invented the Pitot tube [1], and in the mid-19^th century, French scientist Henry Darcy modified it to its modern form [2]. In the early 20^th century, German aerodynamicist Ludwig Prandtl combined the static pressure measurement and Pitot tube into the Pitot-static tube, which is widely used today.

A schematic of a Pitot-static tube is shown in Figure 1. There are 2 openings in the tubes: one opening faces the flow directly to sense the stagnation pressure, and the other opening is perpendicular to the flow to measure the static pressure.

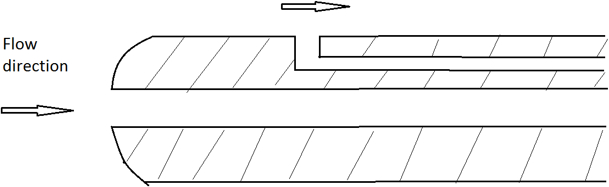
Figure 1. Schematic of a Pitot-static tube.

The pressure differential is required to determine the flow speed, which is typically measured by pressure transducers. In this experiment, a liquid column manometer is used to provide a good visual to measure the change in pressure. The pressure differential is determined as follows:

where Δh is the height difference of the manometer, ρ_L is the density of the liquid in the manometer, and g is the acceleration due to gravity. Combining equations 2 and 3, the flow speed is predicted by:

1. Recording manometer pressure readings with changes in airspeed.

1. Connect the two leads of the Pitot-static tube to the two ports of the manometer. The manometer should be filled with colored oil and marked as water inch graduations.
2. Insert the Pitot-static tube into the threaded fitting so that the sensing head is in the center of the test section of the wind tunnel and the tube is pointing upstream. The test section should be 1 ft x 1 ft, and the wind tunnel should be able to sustain an airspeed of 140 mph.
3. Use an inclinometer to adjust the Pitot-static tube to a zero-degree angle of attack.
4. Run the wind tunnel at 50 mph and then record the pressure difference reading at the manometer.
5. Increase the airspeed in the wind tunnel by 10 mph and record the pressure difference at the manometer.
6. Repeat 1.5 until the airspeed reaches 130 mph. Record all results.

2. Investigate the accuracy of Pitot-static tubes with a positive angle of attack.

1. Use the inclinometer to adjust the angle of attack to positive 4°.
2. Run the wind tunnel at 100 mph, and record the pressure difference reading on the manometer.
3. Increase the angle of attack by 4° increments, and repeat steps 2.1 - 2.2 up to an angle of attack of 28°. Record all results.

Representative results are shown in Table 1 and Table 2. The results of the experiment are in good agreement with the actual wind speed. The Pitot-static tube accurately predicted the airspeed with a maximum percentage of error of approximately 4.2%. This can be attributed to errors in setting the wind tunnel airspeed, errors reading the manometer and instrument errors of the Pitot-static tube.

Table 1. Calculated airspeed and error based on manometer reading at various wind tunnel speeds.

Table 2. Calculated airspeed and error based on manometer reading at various angles of attach.

In Table 2, the percentage error is compared against the zero-angle case in Table 1. The results indicate that the Pitot-static tube is insensitive to misalignment with flow directions. The highest discrepancy occurred at an angle of attack of about 20°. A 3.35% error was obtained with respect to the zero angle reading. As the angle of attack increased, both the stagnation and static pressure measurements decreased. The two pressure readings tend to compensate each other so that the tube yields velocity readings that are accurate to 3 - 4% for angles of attack up to 30°. This is the chief advantage of the Prandtl design over other types of Pitot tubes.

Airspeed information is critical to aviation applications, such as for aircraft and drones. A Pitot-static tube is typically connected to a mechanical meter to show the airspeed at the front panel in the cockpit. For commercial aircraft, it is also connected to the onboard flight control system.

Errors in pitot-static system readings can be extremely dangerous. There are typically 1 or 2 redundant Pitot-static systems for commercial aircraft. To prevent ice buildup, the Pitot tube is heated during flight. Many commercial airline incidents and accidents have been traced to a failure of the Pitot-static system. For example, in 2008 Air Caraibes reported two incidents of Pitot tube icing malfunctions on its A330s [3].

In industry, the airspeed in duct and tubing can be measured with Pitot tubes where an anemometer or other flow meters would be difficult to install. The Pitot tube can be easily inserted through a small hole in the duct.

In this demonstration, the use of Pitot-static tubes was examined in a wind tunnel and the measurements were used to predict airspeed in the wind tunnel. The results predicted by the Pitot-static tube correlated well with the wind tunnel settings. The sensitivity of possible misalignment of the Pitot-static tube was also investigated and it was concluded that the Pitot-static tube is not particularly sensitive to misalignment up to and angle of attack of 28°.