Nella ricerca di identificare una proprietà che può prevedere in modo affidabile la spontaneità di un processo, è stato identificato un candidato promettente: l'entropia. I processi che comportano un aumento dell'entropia del sistema (ΔS > 0) sono molto spesso spontanei; tuttavia, gli esempi contrari sono abbondanti. Espandendo la considerazione dei cambiamenti di entropia per includere l'ambiente circostante, è possibile raggiungere una conclusione significativa riguardo alla relazione tra questa proprietà e spontaneità. Nei modelli termodinamici, il sistema e l'ambiente circostante comprendono tutto, cioè l'universo, e quindi è vero quanto segue:

Per illustrare questa relazione, considerare nuovamente il processo di flusso di calore tra due oggetti, uno identificato come sistema e l'altro come l'ambiente circostante. Ci sono tre possibilità per un tale processo:

1. Gli oggetti sono a temperature diverse e il calore scorre dal più caldo all'oggetto più fresco. Questo si osserva sempre spontaneamente. Designando l'oggetto più caldo come sistema e invocando la definizione di entropia si ottiene quanto segue:

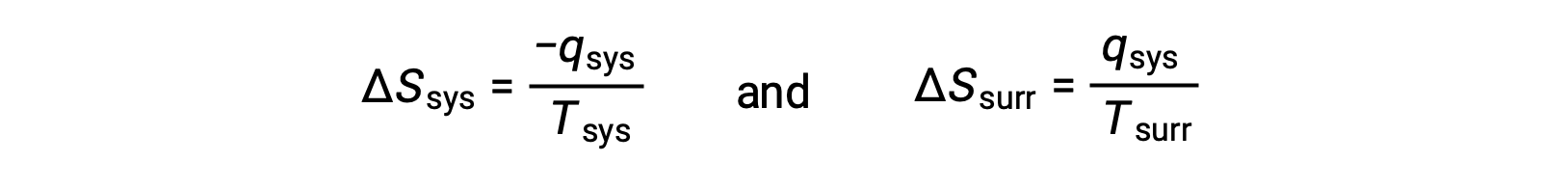
Le magnitudini di −q_{sys e} q sys sono uguali, i loro segni aritmetici opposti che denotano la perdita di calore da parte del sistema e il guadagno di calore da parte dell'ambiente circostante. Poiché T_sys > T_surr in questo scenario, la diminuzione dell'entropia del sistema sarà inferiore all'aumento dell'entropia dell'ambiente circostante, e quindi l'entropia dell'universo aumenterà:

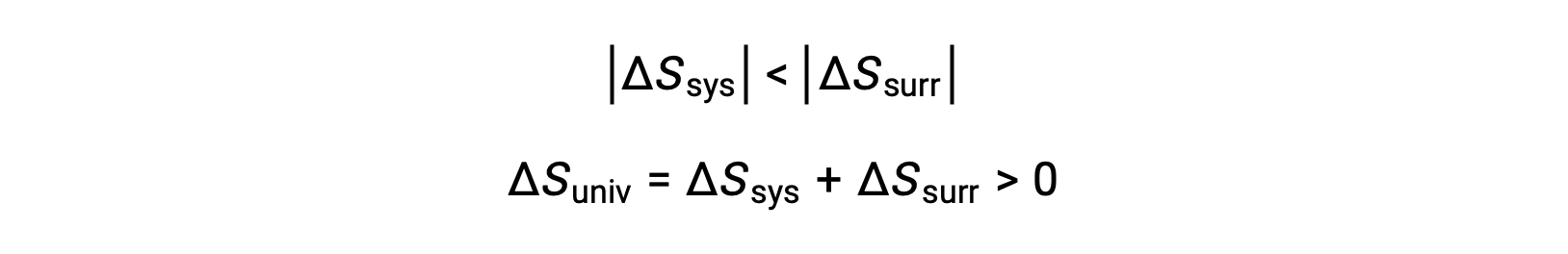
2. Gli oggetti sono a temperature diverse e il calore scorre dal dispositivo di raffreddamento all'oggetto più caldo. Questo non si osserva mai spontaneamente. Ancora una volta designando l'oggetto più caldo come sistema e invocando la definizione di entropia si ottiene quanto segue:

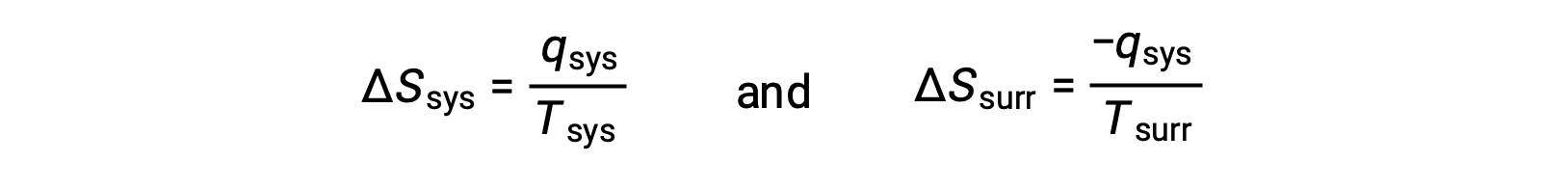
i segni aritmetici_{del sistema} q denotano il guadagno di calore da parte del sistema e la perdita di calore da parte dell'ambiente circostante. La grandezza del cambiamento di entropia per l'ambiente circostante sarà di nuovo maggiore di quella per il sistema, ma in questo caso, i segni dei cambiamenti di calore (cioè la direzione del flusso di calore) produrranno un valore negativo per ΔS_univ. Questo processo comporta una diminuzione dell'entropia dell'universo.

3. Gli oggetti sono essenzialmente alla stessa temperatura, T_sys ≈ T_surr, e quindi le magnitudini dei cambiamenti di entropia sono essenzialmente le stesse sia per il sistema che per l'ambiente circostante. In questo caso, il cambiamento di entropia dell'universo è zero, e il sistema è in equilibrio.

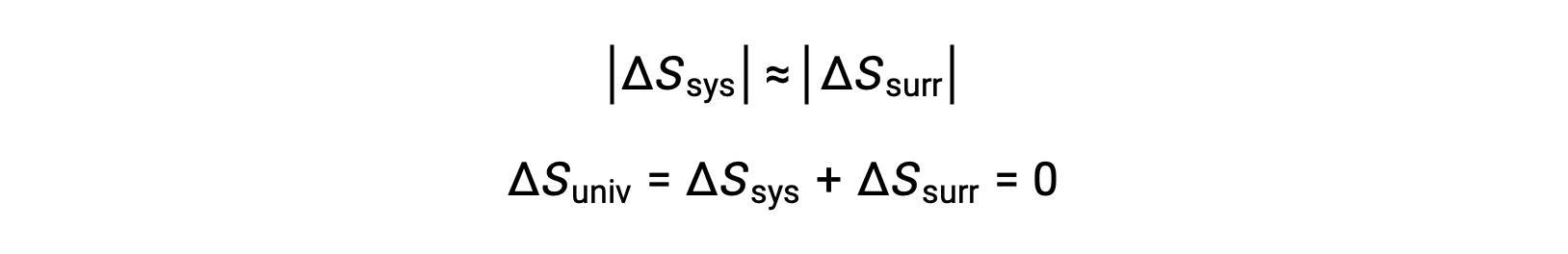
Questi risultati portano ad una profonda affermazione riguardo alla relazione tra entropia e spontaneità nota come seconda legge della termodinamica: tutti i cambiamenti spontanei causano un aumento dell'entropia dell'universo. Una sintesi di queste tre relazioni è fornita nella tabella seguente.

La seconda legge della termodinamica
ΔSuniv > 0	Spontanea
ΔSuniv < 0	nonpontaneo (spontaneo in direzione opposta)
ΔSuniv = 0	all'equilibrio

Per molte applicazioni realistiche, l'ambiente circostante è vasto rispetto al sistema. In questi casi, il calore guadagnato o perso dall'ambiente circostante come risultato di alcuni processi rappresenta una frazione molto piccola, quasi infinitesimale, della sua energia termica totale. Ad esempio, la combustione di un combustibile nell'aria comporta il trasferimento di calore da un sistema (le molecole di carburante e ossigeno in reazione) a un ambiente infinitamente più massiccio (l'atmosfera terrestre). Di conseguenza, q_{surr è} una buona approssimazione di q_syse la seconda legge può essere indicata come segue:

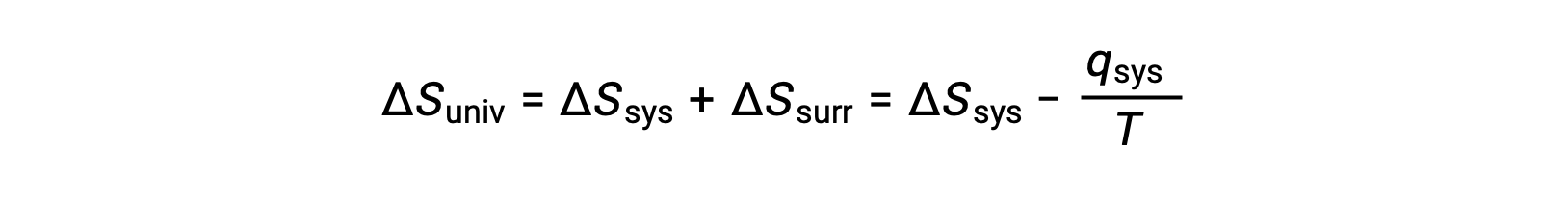
Questa equazione è utile per prevedere la spontaneità di un processo.

Questo testo è adattato da Openstax, Chimica 2e, Capitolo 16.2: La seconda e terza legge della termodinamica.