Raffreddamento ed ebollizione

Fonte: Alexander S Rattner, Sanjay Adhikari e Mahdi Nabil; Dipartimento di Ingegneria Meccanica e Nucleare, The Pennsylvania State University, University Park, PA

Il riscaldamento controllato seguito da un rapido raffreddamento è un elemento importante di molte applicazioni di lavorazione dei materiali. Questa procedura di trattamento termico può aumentare la durezza del materiale, che è importante per utensili da taglio o superfici in ambienti ad alta usura. La fase di raffreddamento rapido è chiamata temprae viene spesso eseguita immergendo i materiali in un bagno fluido (spesso acqua o olio). Il trasferimento di calore di spegnimento può verificarsi a causa della convezione forzata - quando l'azione del materiale in rapido movimento attraverso il refrigerante guida il processo di trasferimento del calore e a causa della convezione libera - quando la ridotta densità del fluido caldo vicino alla superficie del materiale provoca la circolazione guidata dalla galleggiabilità e il trasferimento di calore. A temperature elevate del materiale, il refrigerante può bollire, portando ad una maggiore efficacia del trasferimento di calore. Tuttavia, quando i materiali estremamente caldi vengono temprati, possono essere ricoperti da vapore di refrigerante a conduttività termica relativamente bassa, portando a uno scarso trasferimento di calore.

In questo esperimento, il trasferimento di calore di tempra sarà misurato per un cilindro di rame riscaldato, che è rappresentativo di piccole parti trattate termicamente. Il profilo di temperatura del campione transitorio verrà misurato durante la tempra e confrontato con i risultati teorici per il trasferimento di calore a convezione libera. I fenomeni di ebollizione saranno anche indagati qualitativamente.

Il processo di tempra del trasferimento di calore è fondamentalmente transitorio. In generale, la distribuzione della temperatura può variare nello spazio e nel tempo all'interno di un campione di materiale raffreddato. Tuttavia, se la resistenza termica a conduzione interna è piccola rispetto alla resistenza termica esterna dalla superficie del campione al fluido circostante (convezione), si può presumere che il campione abbia una temperatura quasi uniforme in qualsiasi istante, semplificando l'analisi. Questa condizione può essere espressa in termini di numero Biot (Bi), che confronta la resistenza di conduzione interna con la resistenza di convezione esterna. Generalmente, quando Bi < 0,1, la resistenza al trasferimento di calore interno può essere assunta trascurabile rispetto alla resistenza esterna al trasferimento di calore.

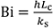(1)

Qui, h è il coefficiente di convezione esterno, k_s è la conduttività termica del campione e L_c è una scala di lunghezza caratteristica del campione. h può essere previsto utilizzando modelli di trasferimento di calore e adattamenti di curve pubblicati in letteratura per diverse condizioni e fluidi. In questo esperimento, h sarà misurato e confrontato con i risultati previsti con i modelli pubblicati (vedere la sezione Risultati rappresentativi).

Per il cilindro di rame qui considerato (k = 390 W m^-1 K^-1, diametro D = 9,53 mm, lunghezza L = 24 mm), la scala di lunghezza caratteristica è D/2 = 4,8 mm. Assumendo un coefficiente di convezione massimo di h = 5000 W m^-2 K^-1, il numero di Biot di picco sarebbe 0,06. Poiché questo numero è piccolo (< 0,1), è ragionevole supporre che le resistenze di conduzione interne siano trascurabili e che il campione abbia una temperatura uniforme. A valori Bi più elevati, è necessaria un'analisi più complicata che tenga conto della variazione di temperatura nel materiale.

Assumendo un campione a temperatura uniforme, la velocità di trasferimento del calore può essere modellata bilanciando la perdita di energia interna dal campione con la velocità di rimozione del calore convettivo dalla legge di raffreddamento di Newton. Questo approccio è chiamato analisi della capacità raggruppata.

(2)

Qui, m è la massa del campione (15 g), c è il calore specifico del materiale campione (385 J kg -1 K^-1 per il rame), T_s è la temperatura del campione, A_s è l'area della superficie del campione (8,6 × 10^-4 m²) e è la 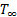temperatura del fluido circostante.

Per prevedere la velocità di raffreddamento (dT_s/ dt) durante la tempra, è necessario prevedere anche il coefficiente di convezione (h). Se il campione è al di sotto della temperatura di ebollizione del fluido e tenuto fermo in una piscina di refrigerante, il calore viene rimosso principalmente per convezione libera. In questa modalità, la circolazione e il raffreddamento sono prodotti dall'aumento guidato dalla galleggiabilità del fluido riscaldato vicino al campione. Maggiori differenze di temperatura tra campione e fluido comportano un aumento dei tassi di circolazione.

Se la temperatura del campione è superiore al punto di ebollizione, il vapore può essere generato in superficie, con conseguenti velocità di raffreddamento significativamente più elevate. Durante l'ebollizione, le bolle di vapore si formano e crescono da piccole imperfezioni (siti di nucleazione) sulla superficie calda. A temperature superficiali più elevate, più siti di nucleazione diventano attivi, con conseguenti maggiori coefficienti di convezione e velocità di trasferimento del calore più elevate. Tuttavia, a temperature molto elevate, il vapore di conduttività relativamente bassa non può essere rimosso abbastanza velocemente. Ciò si traduce nella crisi di ebollizione, in cui il raffreddamento superficiale è limitato a causa dell'isolamento dal vapore, riducendo la velocità di trasferimento del calore.

NOTA: questo esperimento utilizza il riscaldamento a fiamma. Assicurarsi che un estintore sia a portata di mano e che nessun materiale infiammabile sia vicino all'esperimento. Seguire tutte le precauzioni standard per la sicurezza antincendio.

1. Fabbricazione del campione per la tempra (vedi fotografia, Fig. 1)

1. Tagliare una piccola lunghezza (~ 24 mm) di asta di rame di 9,53 mm di diametro. Praticare due piccoli fori (diametro 1,6 mm) circa a metà strada nell'asta vicino alle due estremità. Questi fori saranno i pozzetti delle termocoppie. Poiché i fori e le termocoppie sono relativamente piccoli, possiamo supporre che abbiano un effetto minimo sul comportamento complessivo del trasferimento di calore.
2. Utilizzare resina epossidica ad alta temperatura(ad esempio,JB Kwik) per apporre sonde termocoppia ad alta temperatura nei due fori. Assicurarsi che le punte della sonda della termocoppia siano premute al centro del campione di rame mentre la resina epossidica si imposta.
3. Impostare un contenitore per l'acqua come bagno di spegnimento. Inserire una terza termocoppia di riferimento nel bagno vicino a dove verrà spento il campione.
4. Collegare le tre termocoppie a un sistema di acquisizione dati. Impostare un programma (ad esempio in LabVIEW) per registrare le misurazioni della temperatura transitoria in un foglio di calcolo.

Figura 1: a. Fotografia di un campione di rame strumentato nel bagno d'acqua di raffreddamento.b. Campione di rame riscaldante.

2. Esecuzione dell'esperimento

1. Posizionare un bruciatore Bunsen o un contenitore di combustibile sfregamento accanto al bagno di tempra. Accendi la fiamma.
2. Da una distanza di sicurezza, riscaldare gradualmente il campione sulla fiamma (a ~ 50 ° C consigliato per il primo esperimento). Il campione può essere trattenuto dai conduttori della termocoppia (Fig. 1b).
3. Inizia a registrare i dati della termocoppia da archiviare e immergi il campione nel bagno di spegnimento. Tenere il campione fermo in modo che il trasferimento di calore a convezione forzata sia minimo. Interrompere la registrazione dei dati di temperatura una volta che il campione si avvicina entro pochi gradi dalla temperatura del bagno.
4. Ripetere questa procedura per temperature iniziali del campione progressivamente più elevate (fino a ~ 300 ° C). Per i casi superiori a 100°C, osservare il comportamento di ebollizione dopo aver spento il campione.

3. Analisi dei dati

1. Per le misurazioni della temperatura registrate, registrare la temperatura media del campione in ogni momento come media aritmetica delle due letture della termocoppia incorporata.
2. Calcolare la velocità di raffreddamento del campione ad ogni tempo registrato j come 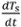= (T_s,j+1-T_s,j)/(t_j+1-t_j) (i valori saranno negativi). Qui, t_j è il tempo di ogni lettura registrata. Può essere utile attenuare queste curve di velocità di raffreddamento eseguendo una media corrente con una finestra di esempio di 2-3 letture.
3. Calcolare i coefficienti sperimentali di scambio termico h con Eqn. 2 utilizzando la velocità di raffreddamento della fase 3.2 e le temperature del bagno misurato (T_∞) e del campione (T_s). In che modo questi coefficienti di scambio termico si confrontano con i valori previsti (Eqn. 4, vedi Risultati)?
4. Per un caso con temperatura iniziale inferiore a 100 °C, utilizzare la misurazione sperimentale iniziale della temperatura e integrare numericamente Eqn. 2 per prevedere il raffreddamento nel tempo. Usa Eqn. 4 per prevedere il coefficiente di convezione in ogni momento. Confrontare questa curva con i valori misurati. Per la dimensione numerica del passo temporale Δt(ad esempio, 0,1 s), la temperatura può essere integrata come:
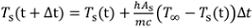   (3)

Le fotografie dell'ebollizione a diverse temperature iniziali del campione (T_s,0) sono presentate in Fig. 2. A T_s,0 = 150°C si formano bolle di vapore che rimangono attaccate al campione. A T_s,0 = 175°C le bolle si staccano e galleggiano nell'acqua. A 200 ° C, vengono generate più bolle e si osservano ulteriori aumenti a temperature più elevate. Eventi di tipo crisi di ebollizione(ad esempio,l'intero campione è circondato da vapore persistente) non sono osservati a causa della bassa temperatura del fluido sfuso (~ 22 ° C).

Quando la temperatura del campione è inferiore alla temperatura di ebollizione del refrigerante (100 °C), è possibile applicare modelli di convezione libera monofase per prevedere il coefficiente di convezione. La velocità di trasferimento del calore a convezione libera dipende dal numero di Prandtl del fluido (Pr), che è il rapporto tra viscosità e diffusività termica (Pr = 6,6 per l'acqua a temperatura ambiente) e dal numero di Rayleigh (Ra), che è una misura del trasporto naturale della convezione:

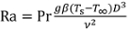(4)

Qui, g è l'accelerazione gravitazionale (9,81 m s^-2), β è il coefficiente di espansione termica del fluido (variazione relativa della densità con la temperatura, 2,28 × 10^-4 K^-1 per l'acqua), e ν è la viscosità cinematica del fluido (9,57 × 10^-7 m² s^-1 per l'acqua). Ad esempio, per il campione di 9,5 mm di diametro a T_s = 75 °C in acqua a T_∞ = 22 °C, il numero di Rayleigh è Ra = 7,44 × 10⁵.

Per un cilindro orizzontale in trasferimento di calore a convezione libera monofase, una formula di convezione ampiamente utilizzata (basata su curve adatte a dati empirici) è presentata nell'equazione 4.

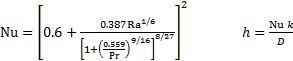(5)

Qui, k è la conduttività termica del fluido (0,60 W m^-1 K^-1 per l'acqua). La formula fornisce il numero di Nusselt (Nu), il coefficiente di scambio termico a convezione adimensionale. Può essere convertito nel coefficiente di scambio termico dimensionale(h in unità W m^-2 K^-1)moltiplicando per k/D. Per il caso di esempio con Ra = 7,44 × 10⁵, questo modello prevede Nu = 16,4 e h = 1040 W m^-2 K^-1.

In Fig. 3, i coefficienti di convezione istantanea misurati vengono confrontati con i valori teorici di convezione libera dell'equazione 4. Un accordo qualitativamente stretto si osserva a temperature superficiali più basse (T_s-T_∞ < 80 K). A temperature del campione più elevate, si verifica l'ebollizione e i valori del coefficiente di trasferimento del calore misurati superano significativamente le previsioni di convezione libera monofase. Il coefficiente di convezione aumenta bruscamente con la temperatura del campione in condizioni di ebollizione. Questo aumento è dovuto al maggior numero di siti di nucleazione attivi a temperature superficiali più elevate.

In Fig. 4, le curve di raffreddamento del campione misurate e previste sono presentate per un caso con temperatura iniziale di 42,5 °C. Inizialmente, la curva di temperatura sperimentale decade più velocemente. Ciò può essere dovuto agli effetti di convezione forzata derivanti dall'inserimento del campione nel bagno. Nel corso del tempo, si osservano lievi oscillazioni nella curva misurata, probabilmente dovute al movimento della persona che detiene il campione. Successivamente, le curve di temperatura sperimentali e previste corrispondono bene.

Figura 2: Fotografie di fenomeni di ebollizione su campione spento ad aumento della temperatura iniziale (T₀)

Figura 3: Confronto dei coefficienti di convezione libera misurati e di convezione di ebollizione con i valori teorici di convezione libera

Figura 4: Confronto della curva di raffreddamento misurata e prevista per caso con temperatura iniziale T₀ = 42,5°C

Questo esperimento ha dimostrato il processo di trasferimento di calore transitorio durante la tempra. La temperatura di un campione di materiale è stata monitorata mentre veniva rapidamente raffreddato a bagnomaria. I coefficienti di convezione e i profili di temperatura nel tempo sono stati confrontati con i valori teorici per il raffreddamento a convezione libera. I fenomeni di ebollizione sono stati discussi e osservati anche per le alte temperature iniziali del campione. Le informazioni provenienti da tali esperimenti e approcci di modellazione dimostrati possono essere applicate per comprendere e progettare processi di trasferimento di calore per la produzione e il trattamento termico dei materiali.

Il raffreddamento rapido a tempra è spesso impiegato negli strumenti di trattamento termico. Alcune leghe di acciaio possono essere ricotto (riscaldate e raffreddate gradualmente) per ridurre la durezza per la lavorazione e la lavorazione. Possono quindi essere riscaldati e raffreddati rapidamente per ottenere un'elevata durezza per il taglio di altri materiali(ad esempio,file, lame per seghe) o in applicazioni ad alta usura(ad esempio,teste di martello, punzoni). Ulteriori operazioni di trattamento termico possono migliorare la tenacità per prevenire guasti fragili.

Più in generale, il riscaldamento e il raffreddamento transitorio rapido si trovano in molte applicazioni. Ad esempio, i processori dei computer si riscaldano rapidamente durante l'esecuzione di programmi ad alta intensità di calcolo. Questo aumento della temperatura spesso innesca una maggiore velocità della ventola e un rapido raffreddamento. Quando le centrali elettriche vengono messe in linea, i tubi dei generatori di vapore subiscono un riscaldamento rapido. In entrambi i casi, la previsione e la caratterizzazione delle velocità di riscaldamento e raffreddamento sono importanti per evitare che i materiali si guastino a causa del surriscaldamento e dell'affaticamento. Le analisi del trasferimento di calore transitorio, come dimostrato in questa indagine, sono fondamentali per l'ingegneria di tali tecnologie.