Mappatura quantitativa della deformazione di un aneurisma dell'aorta addominale
Panoramica
Fonte: Hannah L. Cebull1, Arvin H. Soepriatna1, John J. Boyle2 e Craig J. Goergen1
1 Weldon School of Biomedical Engineering, Purdue University, West Lafayette, Indiana
2 Ingegneria meccanica e scienza dei materiali, Washington University di St. Louis, St Louis, Missouri
Il comportamento meccanico dei tessuti molli, come vasi sanguigni, pelle, tendini e altri organi, è fortemente influenzato dalla loro composizione di elastina e collagene, che forniscono elasticità e forza. L'orientamento delle fibre di queste proteine dipende dal tipo di tessuto molle e può variare da una singola direzione preferita a reti intricate, che possono alterarsi nei tessuti malattiati. Pertanto, i tessuti molli spesso si comportano in modo anisotropico a livello cellulare e di organi, creando la necessità di una caratterizzazione tridimensionale. Lo sviluppo di un metodo per stimare in modo affidabile i campi di deformazione all'interno di tessuti o strutture biologiche complesse è importante per caratterizzare e comprendere meccanicamente la malattia. La deformazione rappresenta il modo in cui i tessuti molli si deformano relativamente nel tempo e può essere descritta matematicamente attraverso varie stime.
L'acquisizione dei dati di immagine nel tempo consente di stimare la deformazione e la deformazione. Tuttavia, tutte le modalità di imaging medico contengono una certa quantità di rumore, il che aumenta la difficoltà di stimare con precisione il ceppo in vivo. La tecnica qui descritta supera con successo questi problemi utilizzando un metodo di stima della deformazione diretta (DDE) per calcolare campi di deformazione 3D che variano spazialmente dai dati dell'immagine volumetrica.
Gli attuali metodi di stima della deformazione includono la correlazione delle immagini digitali (DIC) e la correlazione del volume digitale. Sfortunatamente, DIC può solo stimare con precisione la deformazione da un piano 2D, limitando gravemente l'applicazione di questo metodo. Sebbene utili, i metodi 2D come DIC hanno difficoltà a quantificare la deformazione nelle regioni che subiscono la deformazione 3D. Questo perché il movimento fuori piano crea errori di deformazione. La correlazione digitale del volume è un metodo più applicabile che divide i dati del volume iniziale in regioni e trova la regione più simile del volume deformato, riducendo così l'errore fuori piano. Tuttavia, questo metodo si dimostra sensibile al rumore e richiede ipotesi sulle proprietà meccaniche del materiale.
La tecnica qui dimostrata elimina questi problemi utilizzando un metodo DDE, rendendolo così molto utile nell'analisi dei dati di imaging medico. Inoltre, è robusto a ceppo alto o localizzato. Qui descriviamo l'acquisizione di dati a ultrasuoni 4D volumetrici gated, la sua conversione in un formato analizzabile e l'uso di un codice Matlab personalizzato per stimare la deformazione 3D e le corrispondenti deformazioni Green-Lagrange, un parametro che descrive meglio le grandi deformazioni. Il tensore di deformazione green-lagrange è implementato in molti metodi di stima della deformazione 3D perché consente di calcolare F da un Least Squares Fit (LSF) degli spostamenti. L'equazione seguente rappresenta il tensore di deformazione di Green-Lagrange, E, dove F e I rappresentano rispettivamente il gradiente di deformazione e il tensore di identità del secondo ordine.
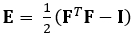 (1)
(1)
Procedura
1. Configurazione ad ultrasuoni 4D
- Quando si utilizza il software di imaging, utilizzare un laptop in grado di eseguire software di calcolo matematico per automatizzare il processo di acquisizione 4D. Collegare il laptop con questo codice personalizzato al sistema ad ultrasuoni tramite la porta USB. Si noti che il software di imaging ha una funzione di ecografia 4D integrata nel software.
- Dopo aver acceso il sistema a ultrasuoni, impostare l'unità di monitoraggio fisiologico assicurandosi anche che i
Risultati
Utilizzando la procedura sopra descritta, è stata acquisita l'ecografia 4D di un aneurisma dell'aorta addominale ad antropo indotto da angiotensina II (AAA) di un topo. Più loop video EKV ad asse corto sono stati acquisiti lungo l'aorta e combinati per creare dati 4D, come mostrato nella Figura 1. Questi dati sono stati quindi convertiti in un file MAT utilizzando un codice personalizzato, che è stato quindi analizzato in un codice di calcolo della deformazione 3D utilizzando una funzione...
Applicazione e Riepilogo
La caratterizzazione meccanica localizzata in vivo è una parte importante della comprensione della crescita e del rimodellamento dei tessuti biologici. Rispetto agli approcci esistenti, la procedura di quantificazione della deformazione qui descritta utilizza un metodo migliorato per calcolare con precisione la deformazione 3D attraverso la deformazione ottimale dell'immagine non deformata prima della correlazione incrociata. Questo metodo non utilizza alcuna ipotesi materiale per determinare i ceppi all'intern.
Vai a...
Video da questa raccolta:

Now Playing
Mappatura quantitativa della deformazione di un aneurisma dell'aorta addominale
Biomedical Engineering
4.6K Visualizzazioni

Imaging di campioni biologici con microscopia ottica e confocale
Biomedical Engineering
35.7K Visualizzazioni

Imaging di campioni biologici con microscopio elettronico a scansione (SEM)
Biomedical Engineering
23.7K Visualizzazioni

Biodistribuzione dei vettori di nanofarmaci: applicazioni del microscopio elettronico a scansione (SEM)
Biomedical Engineering
9.3K Visualizzazioni

Imaging a ultrasuoni ad alta frequenza dell'aorta addominale
Biomedical Engineering
14.4K Visualizzazioni

Tomografia fotoacustica per l'immagine di sangue e lipidi nell'aorta infrarenale
Biomedical Engineering
5.7K Visualizzazioni

Imaging a risonanza magnetica cardiaca
Biomedical Engineering
14.7K Visualizzazioni

Simulazioni fluidodinamiche computazionali del flusso sanguigno in un aneurisma cerebrale
Biomedical Engineering
11.7K Visualizzazioni

Imaging a fluorescenza nel vicino-infrarosso di aneurismi dell'aorta addominale
Biomedical Engineering
8.2K Visualizzazioni

Tecniche non invasive di misurazione della pressione sanguigna
Biomedical Engineering
11.9K Visualizzazioni

Acquisizione e analisi di un segnale ECG (elettrocardiogramma)
Biomedical Engineering
105.1K Visualizzazioni

Resistenza alla trazione dei biomateriali riassorbibili
Biomedical Engineering
7.5K Visualizzazioni

Imaging micro-CT di un midollo spinale di topo
Biomedical Engineering
8.0K Visualizzazioni

Visualizzazione della degenerazione dell'articolazione del ginocchio dopo lesione del LCA non invasiva nei ratti
Biomedical Engineering
8.2K Visualizzazioni

Imaging combinato SPECT e CT per la visualizzazione della funzionalità cardiaca
Biomedical Engineering
11.0K Visualizzazioni