出典:ファイサル・アラムギル、ジョージア工科大学材料工学部、アトランタ、GA

X線回折(XRD)は、材料の原子構造や分子構造を決定するために材料科学で使用される技術です。これは、インシデントX線で材料のサンプルを照射し、材料によって散乱されるX線の強度と散乱角度を測定することによって行われます。散乱X線の強度は散乱角の関数としてプロットされ、材料の構造は、位置の解析、角度、および散乱強度ピークの強度から決定されます。結晶中の原子の平均位置を測定できるだけでなく、実際の構造が理想的なものからどのように逸脱しているか、例えば内部応力や欠陥から生じる情報を、決定することができる。

XRD法の中心となるX線の回折は、一般的なX線散乱現象のサブセットである。XRDは、一般的に広角X線回折(WAXD)を意味するために使用され、弾性散乱X線波を使用するいくつかの方法に該当する。他の弾性散乱ベースのX線技術には、小角X線散乱(SAXS)が含まれます。SAXSは、数ナノメートル以上のスケール(結晶上部構造など)の構造的相関と、薄膜の厚さ、粗さ、密度を測定するX線反射率を測定します。WAXDは10⁰を超える角度範囲をカバーする。

回折ピーク位置と結晶構造の関係:

十分に小さい波長の光波が結晶格子に入ると、格子点から拡散します。発生の特定の角度では、回折された平行波は建設的に干渉し、強度の検出可能なピークを作成します。W.H. Bragg は図 1 に示す関係を特定し、対応する方程式を導き出しました。

nλ = 2d_hkl罪 θ [1]

ここでλは使用するX線の波長であり_、dhklは(hkl)ミラー指数*を有する特定の平面セット間の間隔であり、θは回折ピークが測定される入射角である。最後に、nは回折の「調和の順序」を表す整数である。たとえば、n=1 では、最初の高調波があり、結晶を通して回折されたX線の経路(2d_hkl sinに相当)は正確に1λであり、n=2では回折経路は2λです。通常は n=1 を想定し、一般に θ < sin^-1(2λ/d_h'k'l')の n=1 は、回折実験で最初のピーク (最低 2θ値) を示す平面のミラーインデックスです。 ミラーインデックスは、結晶内の方向と平面を識別するための表記システムを構成する3つの整数のセットです。方向の場合、[h k l]ミラー インデックスは、方向に沿った 2 点のそれぞれの x、y、z 座標 (デカルト座標系) の正規化された差を表します。平面の場合、平面のミラーインデックス(h k l)は、平面に垂直な方向の h k l 値にすぎません。

反射モードの典型的なXRD実験では、X線源は位置に固定され、サンプルはθ上のX線ビームに対して回転します。検出器は回折ビームをピックアップし、2倍の速度で回転させることによってサンプル回転に追いつく必要があります(すなわち、θの所定のサンプル角度については、検出器の角度は2θです)。実験の幾何学的形状を図1に概略的に示す。

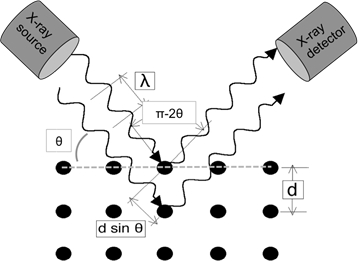
図1:ブラッグの法則のイラスト

強度のピークが観察されると、式1は必ずしも満たされる。その結果、これらのピークが観測される角度に基づいてd-間隔を計算することができます。複数のピークのd間隔を計算することにより、結晶クラスと結晶構造パラメータ材料サンプルは、ハナウォルト検索マニュアルや使用中のXRDソフトウェアで利用可能なデータベースライブラリなどのデータベースを使用して識別することができます。

調査対象のサンプルは単結晶ではないと仮定します。サンプルがサンプル表面に平行な特定の(h*k*l*)面を有する単結晶であった場合、(h*k*l*)のブラッグ条件が満たされるまで回転させ、より高い高調波(h*k*l*)ピーク(n*k*l*)のピーク(n=1の場合)のピークを見るためには、より高い角度で検出できる必要があります。他のすべての角度では、単一の結晶サンプルにピークはありません。代わりに、サンプルが多結晶であるか、または粉末であり、入射X線ビームによって照らされた結晶粒または粉末粒子の統計的に有意な数であると仮定しましょう。この仮定の下で、サンプルはランダムに配向された穀物で構成され、すべての可能な格子面が回折する可能性のある同様の統計的確率を持つ。

d_hkl と単位細胞パラメータの関係は、7つの結晶クラス、立方体、四角形、六角形、菱形、オルソロンビック、単項およびトライクリニックの式2-7に以下に示されています。単位セル パラメータは、7 つの結晶クラスの(a,b,c)の長さと (α, β, γ) の間の角度で構成されます (図 1x は、結晶クラスの 1 つの例を示^{しています。}複数の回折ピーク位置(すなわち、いくつかの異なるd _hkl値)を使用して、単位セルパラメータの値を一意に解決することができる。

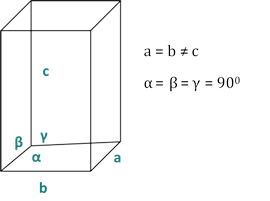
図2:7つの結晶クラスの1つとしての四角形構造。

3 次 (a = b = c; α = β = γ = 90⁰):

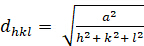[2]

四角形 (a = b ≥ c; α = β = γ = 90⁰):

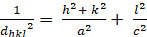[3]

六角形 (a = b ≥ c; α = β = 90⁰; γ = 120⁰):

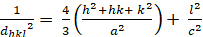[4]

オルソホンビック (a ≥ b ≥ c; α = β = γ = 90⁰):

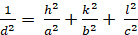[5]

ロンボヘドラル (a = b ≥ c; α = β = γ = 90⁰):

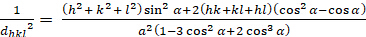[6]

モノクリニック (a ≥ b ≥ c; α = γ = 90⁰≥ β):

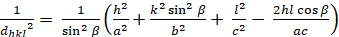[7]

トライクリニック (a ≥ b ≥ c; α ≥ β ≥ γ ≥ 90⁰):

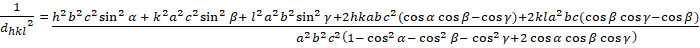      [8]

回折ピーク強度と結晶構造の関係:

次に、XRDパターンの強度に寄与する因子を調べます。因子は、材料の固有の構造的側面(構造内の散乱原子の特定のタイプと位置)および2)材料に固有ではないものから直接生じる散乱への寄与を1)として分解することができる。前者では、「吸収因子」と「構造因子」の2つの要因があります。吸収因子は、主に材料が出入りする途中でX線を吸収する能力に依存します。この因子は、サンプルが薄くない限りθ依存性を持たない(サンプルはX線の減衰長よりも3倍厚くする必要があります)。つまり、異なるピークの強度に対する吸収因子による寄与は一定である。「構造因子」は、構造の直接の結果として特定のピークの強度に直接影響します。残りの因子は、対称的に関連しているために同じファミリに属するすべての平面を占める「多重度」と、XRD実験の幾何学的形状から来る「ローレンツ偏光」因子も影響を及ぼします。ピークの相対的な強度は、材料に固有ではなく、分析式で簡単に説明することができます(すなわち、XRD分析ソフトウェアは、分析機能でそれらを削除することができます)。

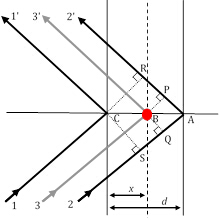
図3:3つの回折線経路は、そのうち11'および22'線がブラッグ条件を満たし、レイ33'は任意の位置に原子(赤い円)によって散乱した結果である。

XRDピークの相対的な強度に材料のユニークな構造寄与を運ぶ唯一の要因として、構造因子は非常に重要であり、より詳しく見る必要があります。図2では、1^次ブラッグ回折条件(これはn=1に相当することを覚えておいてください)が、距離dで区切られたh00方向の2つの原子平面に散乱されるレイ_11'とレイ_22'の間で満たされていると仮定します。この条件では、レイ_11'とレイ_22'のパス長さの差は δ_(22'-11') = SA + AR = λ です。したがって、回折線1と2の間の位相シフトは、Φ22'-11'=(δ(22'-11')/λ)2π=2π(立方対称を仮定し、したがって、h00方向のd=a/h])である。

解析ジオメトリのいくつかのステップで、任意の距離xに間隔を空けた原子の任意の平面によって線 3 が回折される位相シフト_{、Φ (33'-11')}が与えられるように、Φ_(33'-11') = 2π hu、u=x/a(aは(h00)方向の単位セル パラメータ)によって示されます。 他の 2 つの直交方向 (0k0) と (00l) と v=y/a と w=z/a を y 方向と z 方向の分数座標として受け取ると、位相シフトの式は Φ = 2π(hu+kv+lw)まで拡張されます。さて、単位セル内のj-th原子によって散乱されるX線波は_、fjの散乱振幅及び_Φjの位相を有することになっており、それを記述する関数となる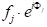。したがって、私たちが求める構造因子は、単位セル内のすべての固有の原子に起因するすべての散乱関数の合計です。この構造係数 F は、次のように指定されます。

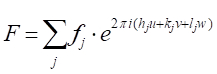[9]

構造係数によって寄与される強度係数は I = F²です。

特定の平面上の原子の位置(u,v,w)(h,k,l)に基づいて、建設的、破壊的、または中間の散乱波間の干渉の可能性があり、この干渉はXRDピークの振幅に直接影響を与えます。(hkl) 平面を表します。

さて、強度のプロット、I、対2θは、XRD実験で測定されるものです。結晶型および関連する単位細胞パラメータ(a、b、c、α、β、γ)の決定は、ピークの系統的な存在/不在を観察し、方程式2~9を用いて、データベースに対して値を比較し、控除および除去のプロセスを用いて分析的に到着させることができる。今日では、これは結晶構造データベースにリンクされた様々なソフトウェアによってかなり自動化されています。

次の手順は、特定のXRD計測器とそれに関連するソフトウェアに適用され、他の計測器を使用する場合は、いくつかのバリエーションがある場合があります。

1. 分析用Alpha-1 XRD機器のNi粉末サンプルを調べます。
2. まず、サンプルの直径に応じてビームサイズを固定するマスクを選択します。ビームは、最小θ値(通常~7 0-100)でサンプルより大きいフットプリントを持つことはできません。幅 ε のサンプルの場合、ビーム サイズは < ε sinθ である必要があります。
3. サンプルスピナーステージにサンプルをロードし、サンプルを所定の位置にロックします。サンプルスピナーは、X線源へのサンプルの露出を空間的にランダム化するのに役立ちます。
4. XRD スキャンの角度範囲を選択します。たとえば、15 ~ 90 度が一般的な範囲です。
5. ステップサイズ、つまり2θの増分、および積分(カウント)時間を選択します。一般に、0.05 度のステップ サイズと 4 秒の統合は、広角スキャンのデフォルトです。
6. この初期スキャンによってすべてのピーク位置が決定されると、その後のスキャンは、これらのピークからの高解像度データが必要な場合、より小さなステップサイズの角度を使用して、特定のピークの周りの狭いスキャン範囲に焦点を当てることができます。

図4では、Ni粉末サンプルのXRDピークを示しています。観測されるピーク ({111}、{200}など) は、 h、 k、および lのすべての偶数またはすべての奇数の組み合わせを持つものに注意してください。Niは顔中心立方体(FCC)であり、すべてのFCC構造において、h、k、およびlが偶数と奇数の整数の混合物である{hkl}平面に対応するピークは、散乱X線の破壊的な干渉のために存在しない。{210}や{211}などの平面に対応するピークが欠落しています。この現象は、体系的な存在と不在のルールと呼ばれ、サンプルの結晶構造を評価するための分析ツールを提供します。

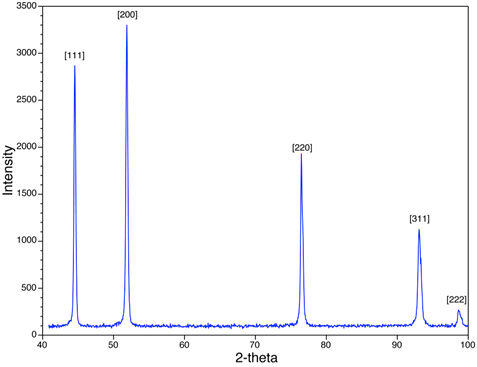
図4:顔中心の立方体構造を持つNiのXRDスキャンを示す。

これは、標準的な XRD 実験のデモンストレーションです。この実験で調べた材料は粉末状でしたが、サンプルがサンプルステージの平面に平行に設定できる平らな表面を持っている限り、XRDは固体材料と同様にうまく機能します。

XRDは、材料における結晶学的秩序の有無(または不在)を決定するためのかなりユビキタスな方法である。結晶構造を決定する標準的な用途を超えて、XRDは、多くの場合、次のようなさまざまな他の構造情報を取得するために使用されます。

1. 材料の構造が非晶質であるかどうか(回折強度の広いこぶと識別可能な結晶学的ピークの欠如によって特徴づけられ)、
2. サンプルが複数の結晶相からなる複合材料であるかどうか、もしそうなら、各相の分率を決定し、
3. 材料が非晶質/結晶性複合体であるかどうかを判断する
4. 材料の粒径/粒径を決定し、
5. 材料のテクスチャの程度(粒の好ましい方向)を決定する。