Quelle: Faisal Alamgir, School of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, GA

Röntgenbeugung (XRD) ist eine Technik, die in der Materialwissenschaft zur Bestimmung der atomaren und molekularen Struktur eines Materials verwendet wird. Dies geschieht, indem eine Probe des Materials mit einfallenden Röntgenstrahlen bestrahlt und dann die Intensitäten und Streuwinkel der Röntgenstrahlen gemessen werden, die vom Material gestreut werden. Die Intensität der gestreuten Röntgenstrahlen wird in Abhängigkeit vom Streuwinkel dargestellt, und die Struktur des Materials wird aus der Analyse der Position, des Winkels und der Intensitäten der streunenden Intensitätsspitzen bestimmt. Neben der Möglichkeit, die durchschnittlichen Positionen der Atome im Kristall zu messen, können Informationen darüber bestimmt werden, wie die tatsächliche Struktur von der idealen abweicht, die sich beispielsweise aus interner Belastung oder aus Defekten ergibt.

Die Beugung der Röntgenstrahlen, die für die XRD-Methode von zentraler Bedeutung ist, ist eine Teilmenge der allgemeinen Röntgenstreuphänomene. XRD, das im Allgemeinen verwendet wird, um zu bedeuten, kann Weitwinkel-Röntgenbeugung (WAXD) können, fällt unter mehrere Methoden, die die elastisch gestreuten Röntgenwellen verwenden. Andere elastische Streutechniken auf Röntgenbasis umfassen die Röntgenstreuung mit kleinen Winkeln (SAXS), bei der die Röntgenstrahlen auf der Probe über den kleinen Winkelbereich von 0,1-10⁰ in der Regel einfallen. SAXS misst strukturelle Korrelationen der Skala von mehreren Nanometern oder größer (z. B. Kristallaufbauten) und Röntgenreflektivität, die die Dicke, Rauheit und Dichte von Dünnschichten misst. WAXD deckt einen Winkelbereich über 10⁰ab.

Beziehung zwischen diffracted Spitzenpositionen und Kristallstruktur:

Wenn Lichtwellen von ausreichend kleiner Wellenlänge auf ein Kristallgitter einfallen, diffraktieren sie von den Gitterpunkten. Bei bestimmten Einfallswinkeln stören die diffrierten parallelen Wellen konstruktiv und erzeugen nachweisbare Intensitätsspitzen. W.H. Bragg identifizierte die in Abbildung 1 dargestellte Beziehung und leitete eine entsprechende Gleichung ab:

n n = 2d_hkl sin

Hier bei der Wellenlänge der verwendeten Röntgenstrahlen ist d_hkl der Abstand zwischen einem bestimmten Satz von Ebenen mit (hkl) Miller-Indizes*, und - ist der Einfallswinkel, bei dem ein Beugungsgipfel gemessen wird. Schließlich ist n eine ganze Zahl, die die "harmonische Ordnung" der Beugung darstellt. Bei n=1 haben wir z.B. die erste Oberschwingung, was bedeutet, dass der Pfad der Röntgenstrahlen, der durch den Kristall diffracted wird (entspricht 2d_hkl sin ) genau 1,während bei n=2 der diffrierte Pfad 2'ist. Typischerweise können wir n=1 und im Allgemeinen n=1 für sin^-1(2'/d_h'k'l') annehmen, wobei h'k'l' die Miller-Indizes der Ebenen sind, die den ersten Peak (bei dem niedrigsten 2-Wert) in einem Beugungsexperiment anzeigen. Miller-Indizes sind eine Gruppe von drei ganzzahlwenigen, die ein Notationssystem zum Identifizieren von Richtungen und Ebenen innerhalb von Kristallen bilden. Für Richtungen stellen die [h k l] Miller-Indizes die normalisierte Differenz in den jeweiligen x-, y- und z-Koordinaten (in einem kartesischen Koordinatensystem) von zwei Punkten entlang der Richtung dar. Bei Ebenen sind die Miller-Indizes (h k l) einer Ebene einfach die h k l Werte der Richtung senkrecht zur Ebene.

In einem typischen XRD-Experiment im Reflexionsmodus wird die Röntgenquelle in Position gebracht und die Probe in Bezug auf den Röntgenstrahl über . Ein Detektor nimmt den diffrierten Strahl auf und muss mit der Probenrotation Schritt halten, indem er mit der doppelten Geschwindigkeit rotiert (d. h. für einen gegebenen Probenwinkel von - ist der Detektorwinkel 2 "). Die Geometrie des Experiments ist schematisch in Abbildung 1 dargestellt.

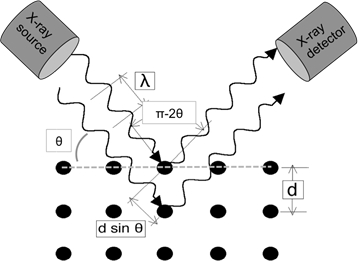
Abbildung 1: Illustration von Braggs Gesetz.

Wenn ein Spitzenwert in der Intensität beobachtet wird, ist Gleichung 1 notwendigerweise erfüllt. Folglich können wir d-Abstände basierend auf den Winkeln berechnen, in denen diese Spitzen beobachtet werden. Durch die Berechnung der d-Spacings mehrerer Peaks können die Kristallklasse und die Kristallstrukturparameter material sample mithilfe einer Datenbank wie dem Hanawalt Search Manual oder Datenbankbibliotheken identifiziert werden, die mit der verwendeten XRD-Software verfügbar sind.

Wir gehen davon aus, dass es sich bei der untersuchten Probe nicht um einen einzigen Kristall handelt. Wäre die Probe ein einzelner Kristall mit einer bestimmten (h*k*l*) Ebene parallel zur Probenoberfläche, müsste sie gedreht werden, bis die Bragg-Bedingung für die (h*k*l*) erfüllt ist, um eine Spitze in diffracted Intensität (für n=1) mit potenziell höheren harmonischen (h*k*l*) Spitzen (z.B. für n=2) auch in höheren Winkeln nachweisbar zu sehen. Bei allen anderen Winkeln gäbe es keine Spitzen in einer einzigen Kristallprobe. Nehmen wir stattdessen an, dass die Probe entweder polykristallin ist oder dass es sich um ein Pulver handelt, mit einer statistisch signifikanten Anzahl von kristallinen Körnern oder Pulverpartikeln, die durch den einfallenden Röntgenstrahl beleuchtet werden. Unter dieser Annahme besteht die Stichprobe aus zufällig orientierten Körnern, mit einer ähnlichen statistischen Wahrscheinlichkeit für alle möglichen Gitterebenen zu diffract.

Die Beziehungen zwischen dem d_hkl und den Einheitenzellparametern sind unten in den Gleichungen 2-7 für die 7 Kristallklassen, kubisch, tetragonal, sechseckförmig, rhombohedral, orthorhombic, monoclinic und triclinic dargestellt. Die Einheitenzellenparameter bestehen ausLängen von(a,b,c) und den Winkeln zwischen den Kanten der Einheitszellen für die 7 Kristallklassen (Abbildung 1x zeigt das Beispiel einer der Kristallklassen: die tetragonale Struktur, wobei a=bc und s = = 90⁰). Mit mehreren diffragierten Spitzenpositionen (d.h. mehreren unterschiedlichen d_hkl-Werten) können die Werte der Einheitenzellparameter eindeutig gelöst werden.

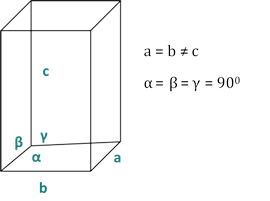
Abbildung 2: Die tetragonale Struktur als eine der sieben Kristallklassen.

Kubisch (a = b = c; n = n = 90⁰):

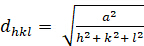[2]

Tetragonal (a = b - c; - = n = 90⁰):

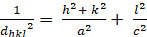[3]

Hexagonal (a = b - c; - = 90⁰; n = 120⁰):

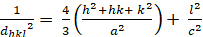[4]

Orthorhombic (a b - c; - = n = 90⁰):

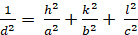[5]

Rhombohedral (a = b - c; - = n = 90⁰):

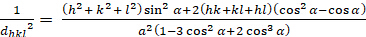[6]

Monoklin (a b - c; - = 90⁰€ )

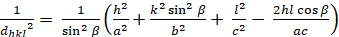[7]

Triklinisch (a b - c; - , 90⁰)

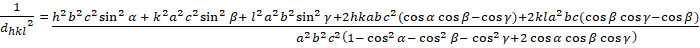      [8]

Beziehung zwischen diffracted Spitzenintensitäten und Kristallstruktur:

Als nächstes untersuchen wir die Faktoren, die zur Intensität in einem XRD-Muster beitragen. Die Faktoren können als 1) den Beitrag zur Streuung aufschlüsseln, der sich direkt aus den einzigartigen strukturellen Aspekten des Materials ergibt (die spezifischen Typen und Positionen von Streuatomen in der Struktur) und 2) denen, die nicht spezifisch für das Material sind. Im ersten Fall gibt es zwei Faktoren: den "Absorptionsfaktor" und den "Strukturfaktor". Der Absorptionsfaktor hängt in erster Linie von der Fähigkeit des Materials ab, Röntgenstrahlen auf ihrem Weg ein- und ausgehen zu absorbieren. Dieser Faktor hat keine Abhängigkeit, solange die Proben nicht dünn sind (die Probe sollte > 3-mal dicker sein als die Dämpfungslänge der Röntgenstrahlen). Mit anderen Worten, der Beitrag des Absorptionsfaktors zur Intensität verschiedener Spitzen ist konstant. Der "Strukturfaktor" wirkt sich direkt auf die Intensität bestimmter Spitzen als direkte Folge der Struktur aus. Die übrigen Faktoren, die "Multiplizität", die alle Ebenen, die zur gleichen Familie gehören, weil sie symmetrisch verwandt sind, und der Faktor "Lorentz-Polarisierung", der aus der Geometrie des XRD-Experiments stammt, wirken sich auch auf die relative Intensität der Spitzen, aber sie sind nicht spezifisch für ein Material und können leicht mit analytischen Ausdrücken berücksichtigt werden (d.h. XRD-Analysesoftware kann sie mit analytischen Funktionen entfernen).

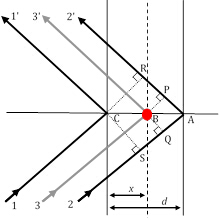
Abbildung 3: Drei Beugungsstrahlpfade, von denen die Strahlen 11' und 22' die Bragg-Bedingung erfüllen, während Strahl 33' aus der Streuung durch ein Atom (roter Kreis) an einer beliebigen Position resultiert.

Als einziger Faktor, der den einzigartigen strukturellen Beitrag eines Materials zu den relativen Intensitäten von XRD-Spitzen trägt, ist der Strukturfaktor sehr wichtig und erfordert einen genaueren Blick. In Abbildung 2 nehmen wir an, dass die Bragg-Beugungsbedingung^1. Ordnung (denken Sie daran, dass dies n=1 entspricht) zwischen Strahl_11' und Strahl_22' erfüllt ist, die auf zwei atomaren Ebenen in h00-Richtung (unter Verwendung der zuvor beschriebenen Miller-Indizes-Notation) verstreut sind, die durch einen Abstand d getrennt sind. Unter dieser Bedingung beträgt der Unterschied in der Bahnlänge zwischen Strahl_11' und Strahl_{22' (22'-11')} = SA + AR = . Die Phasenverschiebung zwischen den diffrierten Strahlen 1 und 2 ist daher_22'-11' =_(22'-11')/') 2' =2' (unter der Annahme einer kubischen Symmetrie und daher d = a/h in h00-Richtung].

Mit wenigen Schritten in der analytischen Geometrie kann gezeigt werden, dass die Phasenverschiebung,_33'-11'), mit strahl 3 diffracted durch eine beliebige Ebene von Atomen, dieeinen beliebigen Abstand xsind, gegeben wird durch: Unter Berücksichtigung der beiden anderen orthogonalen Richtungen (0k0) und (00l) und v=y/a und w=z/a als Bruchkoordinaten in y- und z-Richtung erstreckt sich der Ausdruck für die Phasenverschiebung bis zu . Nun hat die Röntgenwelle, die durch das j-th-Atom in einer Einheitszelle gestreut wird, eine Streuamplitude von f_j und eine Phase von_j, so dass die Funktion, die sie 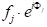beschreibt, ist. Der Strukturfaktor, den wir suchen, ist daher die Summe aller Streufunktionen aufgrund all der einzigartigen Atome in einer Einheitszelle. Dieser Strukturfaktor F wird wie:

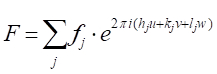[9]

und der Intensitätsfaktor, der durch den Strukturfaktor beigesteuert wird, ist I = F2.

Basierend auf den Positionen (u,v,w) von Atomen auf bestimmten Ebenen (h,k,l) besteht die Möglichkeit von Interferenzen zwischen zerstreuten Wellen, die konstruktiv, zerstörerisch oder dazwischen sind, und diese Interferenz wirkt sich direkt auf die Amplitude der XRD-Spitzen aus. die (hkl) Ebenen darstellen.

Nun, ein Diagramm der Intensität, I, im Vergleich zu 2, ist das, was in einem XRD-Experiment gemessen wird. Die Bestimmung des Kristalltyps und der zugehörigen Einheitenzellparameter(a, b, c, , , und )kann analytisch erreicht werden, indem die systematische Anwesenheit/Abwesenheit von Peaks beobachtet wird, wobei die Gleichungen 2-9 verwendet werden, Werte mit Datenbanken verglichen werden, wobei Abzug und ein Prozess der Eliminierung verwendet werden. Heutzutage ist dieser Prozess ziemlich automatisiert durch eine Vielzahl von Software mit Kristallstruktur-Datenbanken verbunden.

Das folgende Verfahren gilt für ein bestimmtes XRD-Instrument und die zugehörige Software, und es kann einige Variationen geben, wenn andere Instrumente verwendet werden.

1. Wir werden eine Ni-Pulverprobe auf einem panalytischen Alpha-1 XRD-Instrument untersuchen.
2. Wählen Sie zunächst die Maske aus, um die Strahlgröße entsprechend Ihrem Probendurchmesser zu fixieren. Der Strahl darf keinen Footprint haben, der größer als die Probe mit dem kleinsten Wert ist (in der Regel 7⁰-10⁰). Bei einer Probe der Breite sollte die Balkengröße < sin.
3. Laden Sie die Probe in die Probenspinnerstufe, und sperren Sie die Probe in Position. Der Probenspinner hilft, die Exposition der Probe gegenüber der Röntgenquelle räumlich zu randomisieren.
4. Wählen Sie den Winkelbereich für Ihren XRD-Scan aus. Zum Beispiel 15-90 Grad ist ein typischer Bereich.
5. Wählen Sie eine Schrittgröße, d.h. das Inkrement in 2 ,und die Integrationszeit (Zählen). Im Allgemeinen ist eine 0,05-Grad-Schrittgröße und eine Integration von 4 Sekunden die Standardeinstellung für einen Weitwinkel-Scan.
6. Sobald alle Spitzenpositionen durch diesen ersten Scan bestimmt werden, können sich nachfolgende Scans auf einen schmaleren Scanbereich um bestimmte Spitzen konzentrieren, indem eine kleinere Schrittgröße im Winkel verwendet wird, wenn Daten mit höherer Auflösung von diesen Spitzen gewünscht werden.

In Abbildung 4 sehen wir die XRD-Peaks für die Ni-Pulverprobe. Beachten Sie, dass die beobachteten Spitzen (z.B. {111}, {200}) für spitzen Werte gelten, die entweder alle geraden oder alle ungeraden Kombinationen von h, kund lhaben. Ni ist flächenzentrierte Kubik (FCC), und in allen FCC-Strukturen fehlen die Spitzen, die den Ebenenhklentsprechen, wobei h, kund l Mischungen aus geraden und ungeraden Ganzzahlen sind, aufgrund der zerstörerischen Interferenz der verstreuten Röntgenstrahlen. Spitzen, die Ebenen entsprechen, wie {210} und {211} fehlen. Dieses Phänomen wird als systematische Anwesenheits- und Abwesenheitsregeln bezeichnet und stellt ein analytisches Instrument zur Beurteilung der Kristallstruktur der Probe zur Verfügung.

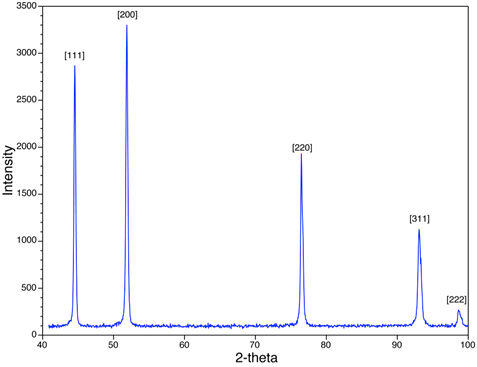
Abbildung 4:Ein XRD-Scan von Ni mit einer flächenzentrierten kubischen Struktur wird angezeigt.

Dies ist eine Demonstration eines Standardmäßigen XRD-Experiments. Das in diesem Experiment untersuchte Material war in Pulverform, aber XRD funktioniert ebenso gut mit festem Material, solange die Probe eine flache Oberfläche hat, die parallel zur Ebene der Probenstufe eingestellt werden kann.

XRD ist eine ziemlich allgegenwärtige Methode zur Bestimmung des Vorhandenseins (oder Fehlens) kristallographischer Ordnung in Materialien. Abgesehen von der Standardanwendung zur Bestimmung der Kristallstruktur wird XRD häufig verwendet, um eine Vielzahl anderer struktureller Informationen zu erhalten, wie z. B.:

1. Ob die Struktur eines Materials amorph ist (gekennzeichnet durch einen breiten Buckel in der Beugungsintensität und einen Mangel an erkennbaren kristallographischen Spitzen),
2. Ob es sich bei der Probe um ein Verbundwerkstoff handelt, das aus mehreren kristallographischen Phasen besteht, und, falls ja, den Anteil jeder Phase bestimmen,
3. Bestimmen, ob ein Material ein amorpher/kristalliner Verbund ist
4. Bestimmung der Korn-/Partikelgröße des Materials,
5. Bestimmung des Texturgrads (bevorzugte Ausrichtung von Körnern) im Material.