קשר בין תנוחות שיא מפוזרות למבנה הגביש:

כאשר גלי אור של אורך גל קטן מספיק הם תקרית על סריג קריסטל, הם מפזרים מנקודות הסריג. בזוויות מסוימות של שכיחות, הגלים המקבילים המפוזרים מפריעים באופן קונסטרוקטיבי ויוצרים פסגות ניתנות לזיהוי בעוצמה. ו.ה. בראג זיהה את מערכת היחסים המאוירת באיור 1 ונובע ממשוואה תואמת:

nλ = 2d_hkl sin θ [1]

הנה אורך הגל של צילומי הרנטגן בהם נעשה שימוש, d_hkl הוא המרווח בין קבוצה מסוימת של מישורים עם מדדי מילר (hkl)*, ו- θ זווית השכיחות שבה נמדדת פסגת עקיפה. לבסוף, n הוא מספר שלם המייצג את 'הסדר ההרמוני' של עקיפה. ב- n = 1, למשל, יש לנו את ההרמוני הראשון, כלומר הנתיב של צילומי רנטגן מפוזרים דרך הגביש (שווה ערך לחטא_hkl 2d ) הוא בדיוק 1λ, בעוד ב n = 2, הנתיב מפוזר הוא 2λ. בדרך כלל אנו יכולים להניח n = 1, ובאופן כללי, n = 1 עבור θ חטא <^-1(2λ / d_h'k'l'),כאשר h'k'l' הם מדדי מילר של המטוסים המציגים את השיא הראשון (בערך 2θ הנמוך ביותר) בניסוי עקיפה. מדדי מילר הם קבוצה של שלושה מספר שלמים המהווים מערכת זיהוי לזיהוי כיוונים ומישורים בתוך גבישים. לכיוונים, מדדי מילר [h k l] מייצגים את ההפרש מנורמל בקואורדינטות x, y ו- z המתאימות (במערכת קואורדינטות קרטזית) של שתי נקודות לאורך הכיוון. עבור מטוסים, מדדי מילר (h k l) של מישור הם פשוט ערכי h k l של הכיוון בניצב למישור.

בניסוי XRD טיפוסי במצב השתקפות, מקור הרנטגן קבוע במקומו והדגימה מסתובבת ביחס לקרן הרנטגן מעל θ. גלאי מרים את הקרן המפוזרת ועליו לעמוד בקצב סיבוב הדגימה על ידי סיבוב בקצב כפול (כלומר עבור זווית מדגם נתונה של θ, זווית הגלאי היא 2θ). הגיאומטריה של הניסוי מוצגת באופן סכמטי באיור 1.

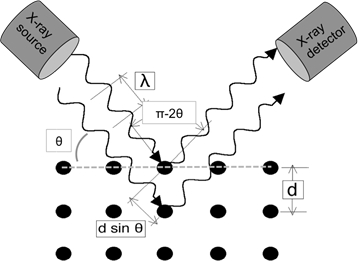
איור 1: איור של חוק בראג.

כאשר נצפתה שיא בעוצמה, משוואה 1 מרוצה בהכרח. כתוצאה מכך, אנו יכולים לחשב d-spacings בהתבסס על הזוויות שבהן פסגות אלה נצפות. על-ידי חישוב המרווחים d של פסגות מרובות, ניתן לזהות את מחלקת הגביש ואת דגימת החומר של הפרמטרים של מבנה הגביש באמצעות מסד נתונים כגון מדריך החיפוש של Hanawalt או ספריות מסד נתונים הזמינות עם תוכנות XRD הנמצאות בשימוש.

אנחנו הנחה שהדגימה הנחקרת היא לא גביש אחד. אם המדגם היה גביש יחיד עם מישור מסוים (h *k*l*) במקביל למשטח המדגם, היה צורך לסובב אותו עד שמצב בראג עבור (h*k*l*) יסוים על מנת לראות שיא בעוצמה מפוזרת (עבור n = 1) עם פסגות הרמוניות גבוהות יותר (h *k *l*) (למשל עבור n = 2) שניתן לזהות גם בזוויות גבוהות יותר. בכל הזוויות האחרות לא יהיו פסגות בדגימת קריסטל אחת. במקום זאת, בואו נניח כי המדגם הוא גם polycrystalline או שזה אבקה, עם מספר משמעותי סטטיסטית של דגנים גבישיים או חלקיקי אבקה מוארים על ידי קרן הרנטגן האירוע. תחת הנחה זו, המדגם מורכב דגנים מכוונים באופן אקראי, עם הסתברות סטטיסטית דומה עבור כל מישורי הסריג האפשריים כדי להעקוף.

הקשרים בין d_hkl לבין הפרמטרים של תא היחידה מוצגים להלן במשוואות 2-7 עבור 7 מחלקות הגביש, מעוקב, טטרגונאלי, משושה, rhombohedral, אורתורומבי, מונוקליני וטריקלין. הפרמטרים של תא היחידה מורכבים מאורכים (a,b,c) וזוויות בין (α, β, γ) הקצוות של תאי היחידה עבור 7 מחלקות הגביש (איור 1x מציג את הדוגמה של אחת ממחלקות הקריסטל: המבנה הטטרגונאלי שבו a=b≠c ו- α=β=γ=90⁰). באמצעות מיקומי שיא מפוזרים מרובים (כלומר מספר ערכי _hkl נפרדים), ניתן לפתור את הערכים של פרמטרי תא היחידה באופן ייחודי.

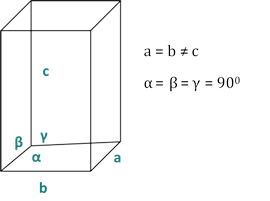
איור 2: המבנה הטטרגוני כאחד משבעת שיעורי הקריסטל.

מעוקב (a = b = c; α = β = γ = 90⁰):

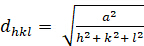[2]

טטרגונאל (a = b ≠ c; α = β = γ = 90⁰):

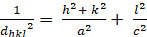[3]

משושה (a = b ≠ c; α = β = 90⁰; γ = 120⁰):

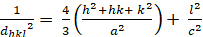[4]

אורתודומבי (a ≠ b ≠ c; α = β = γ = 90⁰):

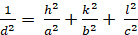[5]

Rhombohedral (a = b ≠ c; α = β = γ = 90⁰):

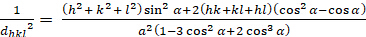[6]

מונוקליני (≠ b ≠ c; α = γ = 90⁰ ≠ β):

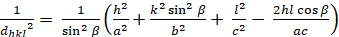[7]

טריקליניק (a ≠ b ≠ c; α ≠ β ≠ γ ≠ 90⁰):

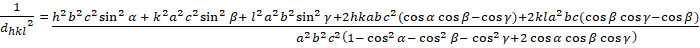      [8]

קשר בין עוצמות שיא מפוזרות למבנה הגביש:

לאחר מכן אנו בוחנים את הגורמים התורמים לעוצמה בתבנית XRD. ניתן לפרק את הגורמים כ-1) את התרומה לפיזור הנובעת ישירות מההיבטים המבניים הייחודיים של החומר (הסוגים והמיקומים הספציפיים של פיזור אטומים במבנה) ו -2) אלה שאינם ספציפיים לחומר. בראשון, ישנם שני גורמים: 'גורם הקליטה' ו'גורם המבנה '. גורם הקליטה תלוי בעיקר ביכולתו של החומר לספוג צילומי רנטגן בדרכם פנימה והחוצה. גורם זה אין תלות θ כל עוד הדגימות אינן דקות (המדגם צריך להיות > 3 פעמים עבה יותר מאשר אורך ההחלכה של צילומי הרנטגן). במילים אחרות, התרומה של גורם הקליטה לעוצמת הפסגות השונות היא קבועה. 'גורם המבנה' משפיע ישירות על עוצמת הפסגות הספציפיות כתוצאה ישירה מהמבנה. הגורמים הנותרים, "ריבוי", אשר מהווה את כל המישורים השייכים לאותה משפחה מכיוון שהם קשורים סימטרית, וגורם 'לורנץ-קיטוב', שמקורו בגיאומטריה של ניסוי XRD, משפיעים גם על העוצמה היחסית של הפסגות אך הם אינם ספציפיים לחומר וניתן בקלות להסביר אותם עם ביטויים אנליטיים (כלומר תוכנת ניתוח XRD יכולה להסיר אותם עם פונקציות אנליטיות).

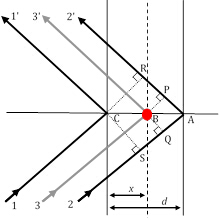
איור 3: שלושה נתיבי קרן עקיפה, מהם קרניים 11' ו-22' מספקות את מצב בראג, בעוד שקרן 33' נובעת מפיזור על ידי אטום (עיגול אדום) בתנוחה שרירותית.

כגורם היחיד שנושא את התרומה המבנית הייחודית של חומר לעוצמות היחסיות של פסגות XRD, גורם המבנה חשוב מאוד ודורש מבט מקרוב. באיור 2, הבה נניח שמצב עקיפה של בראג מסדר¹ (זכור, שזה מתאים ל- n=1) מרוצה בין_{קרניים 11'} לקרן_22' הפזורות בשני מישורים אטומיים בכיוון h00 (באמצעות מדדי מילר שתוארו קודם לכן) מופרדים על-ידי מרחק d. בתנאי זה, ההבדל באורך הנתיב בין ray_11' ו- ray_22' הוא δ_(22'-11') = SA + AR = λ. הסטת הפאזה בין הקרניים המפוזרות 1 ו- 2 היא, אם כן, Φ_22'-11' = (δ_(22'-11')/λ) 2π = 2π (בהנחה של סימטריה מעוקבת, ולכן, d = a/h בכיוון h00].

עם כמה שלבים בגיאומטריה אנליטית, ניתן להראות כי שינוי הפאזה, Φ_(33'-11'), עם קרניים 3 מפוזרות על ידי מישור שרירותי של אטומים המרווחים מרחק שרירותי x, ניתנת על-ידי: Φ_(33'-11') = 2πhu, כאשר u = x/a (a הוא פרמטר תא היחידה בכיוון (h00).) אם ניקח את שני כיווני האורתוגונל האחרים, (0k0) ו- (00l), ו- v = y/a ו- w = z/a כקואורדינטות שבר בכיווני y ו- z, הביטוי עבור משמרת הפאזה משתרע על Φ = 2π(hu +kv + lw). עכשיו, גל הרנטגן הפזור על ידי האטום j-thבתא יחידה יהיה משרעת פיזור של f_j ושלב של Φ_j, כך הפונקציה המתארת את זה היא 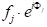. גורם המבנה שאנו מחפשים, אם כן, הוא הסכום של כל פונקציות הפיזור בשל כל האטומים הייחודיים בתא יחידה. גורם מבנה זה, F, ניתן כ:

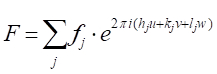[9]

וגורם האינטנסיביות שתרם גורם המבנה הוא I = F².

בהתבסס על מיקומם (u,v,w) של אטומים במישורים מסוימים (h,k,l), קיימת אפשרות להפרעה בין גלים מפוזרים שהם קונסטרוקטיביים, הרסניים או בין לבין, והפרעה זו משפיעה ישירות על המשרעת של פסגות ה- XRD המייצגות את המישורים (hkl).

עכשיו, חלקה של עוצמה, אני, לעומת 2θ הוא מה שנמדד בניסוי XRD. ניתן להגיע לקביעת סוג הגביש ולפרמטרים הקשורים לתא היחידה (a, b, c, α, β ו- γ) על ידי התבוננות בנוכחות שיטתית/היעדר פסגות, באמצעות המשוואות 2-9, השוואת ערכים מול מסדי נתונים, באמצעות ניכוי ותהליך של אלימינציה. כיום, זהו תהליך הוא אוטומטי למדי על ידי מגוון רחב של תוכנות המקושרות למסדי נתונים מבנה קריסטל.

באיור 4 אנו רואים את פסגות ה-XRD לדגימת אבקת Ni. שים לב כי הפסגות שנצפו (למשל {111}, {200}) הן עבור אלה שיש להם את כל השילובים הזוגיים או המוזרים של h, k, ו- l. Ni הוא מעוקב ממוקד פנים (FCC), ובכל המבנים FCC, הפסגות המתאימות למישורים {hkl} שבהם h, k, ו- l הם תערובות של מספר שלמים זוגיים ומוזרים, נעדרים עקב ההפרעה ההרסנית של צילומי הרנטגן הפזורים. פסגות המתאימות למטוסים, כגון {210} {211} חסרות. תופעה זו נקראת כללי נוכחות והיעדרות שיטתיים, והם מספקים כלי אנליטי להערכת מבנה הגביש של המדגם.

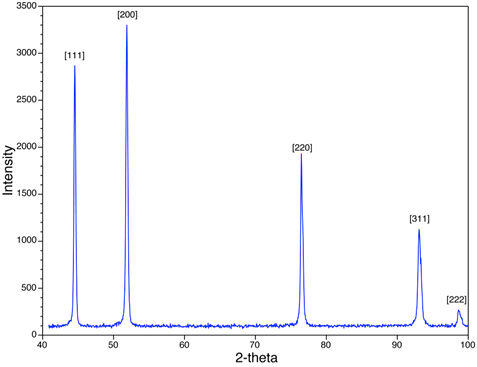
איור 4: מוצגת סריקת XRD של Ni עם מבנה מעוקב במרכז הפנים.

זוהי הדגמה של ניסוי XRD סטנדרטי. החומר שנבדק בניסוי זה היה בצורת אבקה, אך XRD עובד באותה מידה עם פיסת חומר מוצקה כל עוד לדגימה יש משטח שטוח שניתן להגדיר במקביל למישור של שלב המדגם.

XRD היא שיטה בכל מקום בקביעת נוכחות (או היעדר) של סדר קריסטלוגרפי בחומרים. מעבר ליישום הסטנדרטי של קביעת מבנה הגביש, XRD משמש לעתים קרובות כדי להשיג מגוון רחב של מידע מבני אחר כגון:

1. בין אם מבנה החומר הוא אמורפי ובין אם לאו (המאופיין בדבשת רחבה בעוצמת עקיפה והיעדר פסגות קריסטלוגרפיות ניכרות),
2. בין אם המדגם הוא חומר מורכב משלבים קריסטלוגרפיים מרובים, ואם כן, לקבוע את השבר של כל שלב,
3. קביעה אם חומר הוא קומפוזיציה אמורפית/גבישית
4. קביעת גודל התבואה/חלקיק של החומר,
5. קביעת מידת המרקם (אוריינטציה מועדפת של דגנים) בחומר.