衍射峰位置与晶体结构的关系:

当波长足够小的光波在晶格上发生时，它们会从晶格点衍射。在某些入射角度，衍射平行波建设性地干扰并产生可探测的强度峰值。W.H. Bragg 确定了图 1 所示的关系，并推导出了相应的方程:

n = = 2d_hkl辛 [ 1]

此处 * 是使用的 X 射线的波长，d_hkl是具有（hkl） Miller 指数* 的特定平面集之间的间距*，而α是测量衍射峰的发生率角。最后，n 是表示衍射的"谐波顺序"的整数。例如，在n=1，我们有第一次谐波，这意味着X射线通过晶体（相当于_2dhkl sin）的路径正好是1μ，而在n=2，衍射路径是2°。我们通常可以假设 n=1，通常 n=1 表示[lt; sin^-1（2+/d_{h'k'l'）]，}其中 h'k'l'是显示衍射实验中第一个峰值（在最低 2° 值）的平面的 Miller 索引。Miller 指数是一组三个整数，构成用于识别晶体中方向和平面的符号系统。对于方向，[h k l] Miller 指数表示沿方向的两个点的分别 x、y 和 z 坐标（在笛卡尔坐标系中）的正一点差。对于平面，平面的 Miller 指数（h k l）只是垂直于平面方向的 h k l 值。

在反射模式下的典型 XRD 实验中，X 射线源固定在位，样品相对于 X 射线光束旋转超过 α。探测器拾起衍射光束，必须以两倍速率旋转，以±的速度保持样品旋转（即，对于给定的样品角度 α，探测器角度为 2°）。实验的几何形状如图 1 所示。

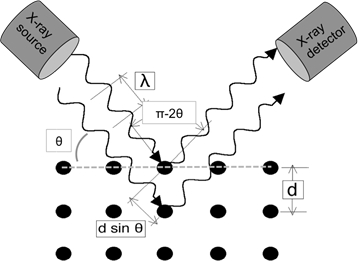
图1:布拉格定律的例证。

当观察到强度的峰值时，方程 1 必然满足。因此，我们可以根据观测这些峰值的角度计算 d 间距。通过计算多个峰的 d 间距，可以使用数据库（如 Hanawalt 搜索手册）或使用的 XRD 软件数据库库来识别晶体类和晶体结构参数材料样本。

我们将假设正在调查的样品不是一个晶体。如果样本是具有与样品表面平行的特定（h_k_l_）平面的单一晶体，则需要旋转，直到满足（h_k_l_）的布拉格条件，才能看到衍射强度（n=1）的峰值，其谐波（h_k_l_）峰值（例如 n=2）在较高角度也能检测到。在所有其他角度，单个晶体样品中没有峰值。相反，让我们假设样品是多晶或粉末，具有统计上显著数量的晶体颗粒或粉末颗粒由事件X射线束照亮。在此假设下，样本由随机定向颗粒组成，所有可能的晶格平面具有类似的统计概率。

d_hkl 和单位细胞参数之间的关系如下，公式 2-7 用于 7 个晶体类、立方、四角、六边形、菱形、胸腔、单临床和三临床。单位单元参数由 7 个晶体类的单位单元边缘的长度 （a、b、c）和角度 （*、 *、 *） 组成（图 1x 显示了其中一个晶体类的示例:a_b_c 和 +=====90⁰）的四角结构。使用多个衍射峰值位置（即几个不同的d_hkl值），可以唯一求解单位单元参数的值。

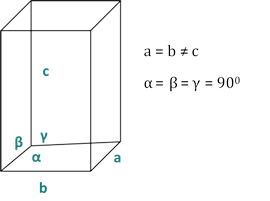
图2:四角结构为七种晶体类之一。

立方 （a = b = c; = = = = = = = 90⁰）:

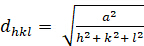[2]

四联体 （a = b + c; √ √ √ √ √ √ √ √ 90⁰）:

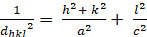[3]

六角形 （a = b + c; = = = = 90^0;= 120⁰）:

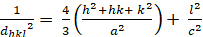[4]

奥索霍比奇 （a + b + c; √ √ √ √ √ √ √ √ 90⁰）:

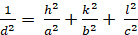[5]

隆博面体 （a = b + c; √ √ √ √ √ √ √ √ √ ） 90⁰）:

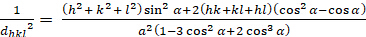[6]

单体诊所 （a = b + c; √ √ √ √ √√ √ √ √ √ √ √ √ ）

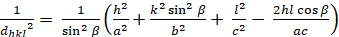[7]

三联诊所 （a + b + c; # # + + + + = = 90⁰）:

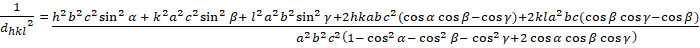      [8]

衍射峰强度与晶体结构的关系:

接下来，我们研究XRD模式中导致强度的因素。这些因素可以分解为 1） 直接来自材料的独特结构方面（结构中散射原子的特定类型和位置）和 2） 对材料不特定于材料的贡献。在前者中，有两个因素:"吸收因子"和"结构因素"。吸收因素主要取决于材料在进出时吸收X射线的能力。只要样品不薄（样品应比 X 射线的衰减长度厚 3 倍），此因子就不存在依赖性。换句话说，吸收因子对不同峰的强度的贡献是恒定的。"结构因子"直接影响特定峰的强度，这是结构的直接结果。其余因子"多重性"，它占属于同一族的所有平面，因为它们是对称相关的，而来自 XRD 实验几何体的"洛伦兹-极化"因子也影响峰的相对强度，但它们不是材料所特有的，并且可以很容易地用分析表达式来解释（即XRD分析软件可以去除它们与分析功能）。

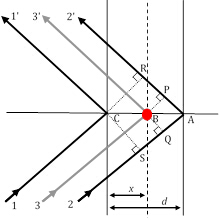
图3:三衍射射线路径，其中光线11'和22'满足布拉格条件，而射线33'的结果是由原子（红色圆圈）在任意位置散射的结果。

作为材料对XRD峰的相对强度的独特结构贡献的唯一因素，结构因子非常重要，需要仔细观察。在图 2 中，我们假设第¹阶布拉格衍射条件（请记住，这对应于 n_1）在光线_11'和射线_22'之间得到满足，它们分散在 h00 方向的两个原子平面上（使用前面描述的 Miller 指数表示法）相隔一个距离 d。在此条件下，射线_11'和射线_22'之间的路径长度差为 ±_{（22'-11'）} = SA = AR = = = 。因此，衍射射线1和2之间的相移是_±22'-11' =_{（+（22'-11'）}/+） 2= = 2°（假设立方对称，因此，d = h00 方向的a/h]。

在分析几何学中，通过几个步骤可以显示，相移_{（[33'-11']）}与射线3衍射的任意对象原子的任意平面，间隔任意距离x，由:[（33'-11'） ]2°hu，其中u_x/a（a是（h00）方向的单位单元参数。以其他两个正交方向（0k0）和（00l）和v_y/a和w_z/a作为y-和z方向中的小数坐标，相移的表达式延伸到+2°（hu_kv_lw）。现在，由j-th原子分散在单元单元中的X射线波将有一个散射振幅f_j和一个相位_=j，这样描述它的函数就是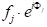。因此，我们寻求的结构因子是单元单元中所有唯一原子的所有散射函数的总和。此结构因子 F 给出如下:

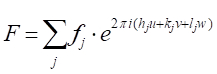[9]

结构因子贡献的强度因子为I=^F2。

根据特定平面（h，k，l）原子的位置（u，v，w），存在存在建设性、破坏性或中间的散射波之间的干扰，这种干扰直接影响XRD峰的振幅代表（hkl）平面。

现在，强度图，I，与2°是XRD实验中测量的。晶体类型和相关单位单元参数（a、b、c、α、α和α）的确定可以通过观察系统存在/峰缺失、使用方程 2-9、将值与数据库进行比较、使用推导和消除过程来进行分析。如今，这个过程是相当自动化的各种软件链接到晶体结构数据库。

在图 4中，我们看到 Ni 粉末样品的 XRD 峰值。请注意，观测到的峰值（例如{111}、{200}）适用于具有h、k和l的所有偶数或全部奇数组合的峰。Ni 是面向面的立方 （FCC），在所有 FCC 结构中，由于散射 X 射线的破坏性干扰，对应于 [hkl]平面的峰值，其中h、k和l是偶数和奇数整数的混合物。缺少与平面对应的峰，如{210}和{211}。这种现象称为系统存在和缺失规则，它们为评估样品的晶体结构提供了一个分析工具。

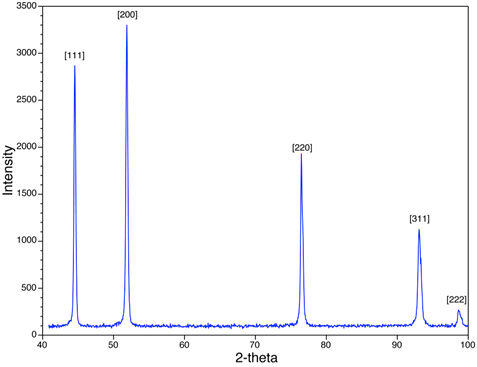
图4:显示了以面为中心的立方结构的NiXRD扫描。

这是标准 XRD 实验的演示。本实验中检验的材料为粉末状，但只要样品具有可与样品级平面平行的平面，XRD与固体材料同样有效。

XRD 是一种相当普遍的方法，用于确定材料中晶体顺序的存在（或不存在）。除了确定晶体结构的标准应用外，XRD 还经常用于获取各种其他结构信息，例如:

1. 材料的结构是否无定形（以衍射强度宽的驼峰和缺乏可辨的晶体峰为特征），
2. 样品是否是由多个晶体相组成的复合材料，如果是，确定每个阶段的分数，
3. 确定材料是否为非晶形/结晶复合材料
4. 确定材料的颗粒/颗粒大小，
5. 确定材料中的纹理程度（颗粒的首选方向）。