어니스트 러더포드와 그의 동료들의 20세기 초에 이어, 핵을 계속 움직이는 가볍고 심지어 티니전자로 둘러싸인 작은 조밀한 핵으로 구성된 원자의 그림이 잘 확립되었습니다. 이 그림은 원자를 태양 궤도를 도는 행성처럼 핵을 도는 전자와 함께 소형 "태양계"로 묘사되었기 때문에 행성 모델이라고 불렸습니다. 가장 간단한 원자는 단일 전자가 이동하는 핵으로 단일 양성자로 구성된 수소입니다. 양성자에 전자를 끌어들이는 정전기력은 두 입자 사이의 거리에만 의존한다. 원자의 이 고전 역학 설명은 불완전합니다, 그러나, 타원형 궤도에서 움직이는 전자는 (방향을 변경하여) 가속될 것이기 때문에, 고전적인 전자기에 따르면, 그것은 지속적으로 전자기 방사선을 방출한다. 궤도 에너지의 이러한 손실은 원자가 본질적으로 불안정하다는 것을 암시하는 핵으로 나선형이 될 때까지 전자의 궤도가 지속적으로 작아지는 결과를 낳아야 합니다.

1913년, 닐스 보어는 수소의 궤도 전자가 지속적으로 빛을 방출할 것이라는 고전 전자기의 예측을 무시함으로써 원자 역설을 해결하려 했다. 대신, 그는 원자 ï1/4 플랑크의 양자화 아이디어와 빛이 자신의 주파수에 비례하는 광자로 구성되어 있다는 아인슈타인의 발견에 대한 고전 역학의 설명을 통합했다. Bohr는 핵을 도는 전자가 일반적으로 방사선 (고정 상태 가설)을 방출하지 는 않지만 다른 궤도로 이동하면 광자가 방출되거나 흡수 될 것이라고 가정했습니다. 흡수되거나 방출되는 에너지는 이 방정식에 따라 궤도 에너지의 차이를 반영합니다.

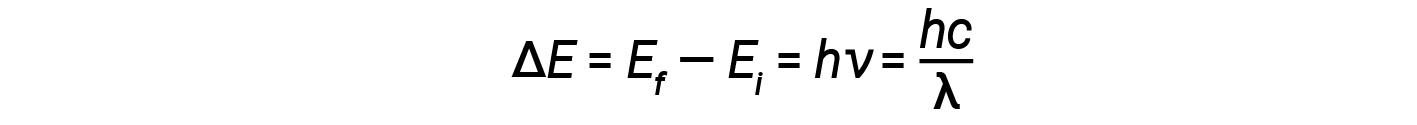
여기서 h는 플랑크의 상수이며 E_i와 E_f는 각각 초기 및 최종 궤도 에너지입니다. 주파수와 파장이 항상 긍정적이기 때문에 에너지 차이의 절대 값이 사용됩니다. Bohr는 에너지의 지속적인 값을 허용하는 대신 이러한 전자 궤도의 에너지가 정량화되었다고 가정했습니다.

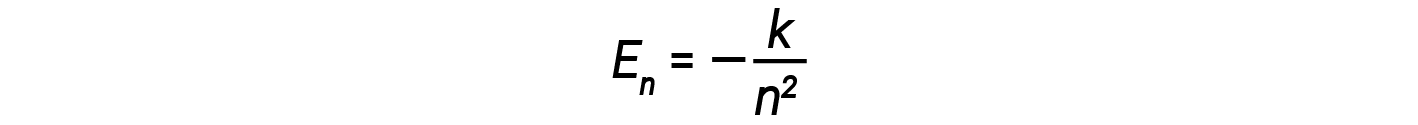
이 표현식에서 k는 전자 질량 및 전하 및 플랑크상수와 같은 기본 상수를 포함하는 상수이다. ΔE에 대한 방정식에 궤도 에너지에 대한 식을 삽입하면

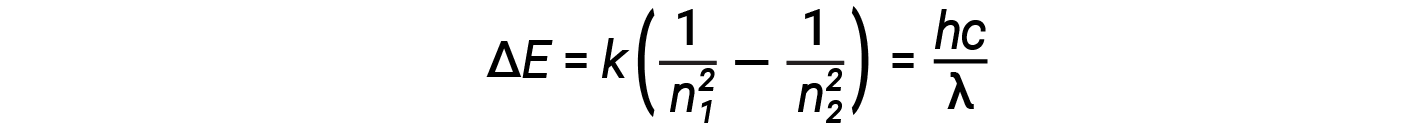
물리학의 기본 법칙 중 하나는 물질이 가능한 가장 낮은 에너지로 가장 안정적이라는 것입니다. 따라서, 수소 원자의 전자는 일반적으로 n = 1 궤도, 가장 낮은 에너지를 가지고 있는 궤도에서 이동한다. 전자가 이 가장 낮은 에너지 궤도에 있을 때, 원자는 지상 전자 상태(또는 단순히 지상 상태)에 있다고 합니다. 원자가 외부 소스로부터 에너지를 받는 경우 전자가 더 높은 n 값을 가진 궤도로 이동할 수 있으며 원자는 이제 더 높은 에너지를 가진 흥분된 전자 상태 (또는 단순히 흥분 상태)에 있게 된다. 전자 전이가 흥분 상태(더 높은 에너지 궤도)에서 덜 흥분된 상태 또는 지상 상태로 발생하면 에너지의 차이가 광자로 방출됩니다. 마찬가지로, 광자의 에너지가 원자에 의해 흡수되면, 광자의 에너지는 더 흥분된 에너지 궤도에서 전자를 이동합니다. 우리는 원자에 있는 전자의 에너지를 우리가 에너지에 관하여 이전에 배운 무슨에 관련시킬 수 있습니다. 에너지 보존의 법칙은 우리가 에너지를 만들거나 파괴할 수 없다고 말합니다. 따라서, 전자를 한 에너지 수준에서 다른 에너지 수준으로 흥분시키기 위해 일정량의 외부 에너지가 필요한 경우 전자가 초기 상태로 돌아오면 동일한 양의 에너지가 해방됩니다.

Bohr의 모델은 단일 전자만 관련되었기 때문에^단일전자 이온에 적용될 수 있으며, 리^{2 +},^{3 +}등은 핵 충전에서만 수소와 다르므로 하나의 전자 원자와 이온은 통칭수소 와 같은 원자라고합니다.

이 텍스트는 Openstax, 화학 2e, 섹션 6.2: 보어 모델에서적용됩니다.