Aby wyświetlić tę treść, wymagana jest subskrypcja JoVE. Zaloguj się lub rozpocznij bezpłatny okres próbny.
Method Article
Visually Based Characterization of the Incipient Particle Motion in Regular Substrates: From Laminar to Turbulent Conditions
W tym Artykule
Podsumowanie
Two different methods for characterizing the incipient particle motion of a single bead as a function of the sediment bed geometry from laminar to turbulent flow are presented.
Streszczenie
Two different experimental methods for determining the threshold of particle motion as a function of geometrical properties of the bed from laminar to turbulent flow conditions are presented. For that purpose, the incipient motion of a single bead is studied on regular substrates that consist of a monolayer of fixed spheres of uniform size that are regularly arranged in triangular and quadratic symmetries. The threshold is characterized by the critical Shields number. The criterion for the onset of motion is defined as the displacement from the original equilibrium position to the neighboring one. The displacement and the mode of motion are identified with an imaging system. The laminar flow is induced using a rotational rheometer with a parallel disk configuration. The shear Reynolds number remains below 1. The turbulent flow is induced in a low-speed wind tunnel with open jet test section. The air velocity is regulated with a frequency converter on the blower fan. The velocity profile is measured with a hot wire probe connected to a hot film anemometer. The shear Reynolds number ranges between 40 and 150. The logarithmic velocity law and the modified wall law presented by Rotta are used to infer the shear velocity from the experimental data. The latter is of special interest when the mobile bead is partially exposed to the turbulent flow in the so-called hydraulically transitional flow regime. The shear stress is estimated at onset of motion. Some illustrative results showing the strong impact of the angle of repose, and the exposure of the bead to shear flow are represented in both regimes.
Wprowadzenie
Incipient particle motion is encountered in a wide range of industrial and natural processes. Environmental examples include the initial process of sediment transport in river and oceans, bed erosion or dune formation among others 1,2,3. Pneumatic conveying4, removal of pollutants or cleaning of surfaces5,6 are typical industrial applications involving the onset of particle motion.
Due to the broad range of applications, the onset of particle motion has been extensively studied over a century, mostly under turbulent conditions7,8,9,10,11,12,13,14,15. Many experimental approaches have been applied to determine the threshold for the onset of motion. The studies include parameters such as the particle Reynolds number13,16,17,18,19,20, the relative flow submergence21,22,23,24 or geometrical factors as the angle of repose16,18,25, exposure to the flow26,27,28,29, relative grain protrusion29 or streamwise bed slope30.
The current data for the threshold including turbulent conditions are broadly scattered12,31 and the results often seem inconsistent24. This is mostly due to the inherent complexity of controlling or determining flow parameters under turbulent conditions13,14. Besides, the threshold for sediment motion strongly depends on the mode of motion, i.e. sliding, rolling or lifting17 and the criterion to characterize the incipient motion31. The latter may be ambiguous in an erodible sediment bed.
During the last decade, experimental researchers have studied incipient particle motion in laminar flows32,33,34,35,36,37,38,39,40,41,42,43,44, where the wide spectrum of length scales interacting with the bed is avoided45. In many practical scenarios implying sedimentation, the particles are quite small and the particle Reynolds number remains lower than about 546. On the other hand, laminar flows are able to generate geometric patterns as ripples and dunes as turbulent flows do42,47. Similitudes in both regimens have been shown to reflect analogies in the underlying physics47 so important insight for the particle transport can be obtained from a better controlled experimental system48.
In laminar flow, Charru et al. noticed that the local rearrangement of a granular bed of uniformly sized beads, so-called bed armouring, resulted in a progressive increase of the threshold for the onset of motion until saturated conditions were achieved32. Literature, however, reveals different thresholds for saturated conditions in irregularly arranged sediment beds depending on the experimental set-up36,44. This scattering may be due to the difficulty of controlling particle parameters such as orientation, protrusion level and compactness of the sediments.
The main goal of this manuscript is to describe in detail how to characterize the incipient motion of single spheres as a function of geometrical properties of the horizontal sediment bed. For that purpose, we use regular geometries, consisting of monolayers of fixed beads regularly arranged according to triangular or quadratic configurations. Regular substrates similar to that we use are found in applications such as for the template-assembly of particles in microfluidic assays49, self-assembly of microdevices in confined structured geometries50 or intrinsic particle-induced transport in microchannels51. More importantly, using regular substrates allows us to highlight the impact of local geometry and orientation and to avoid any dubiety about the role of the neighborhood.
In laminar flow, we observed that the critical Shields number increased by 50% only depending on the spacing between the substrate spheres and thus on the exposure of the bead to the flow38. Similarly, we found that the critical Shields number changed by up to a factor of two depending on the orientation of the substrate to the flow direction38. We noticed that immobile neighbors only affect the onset of the mobile bead if they were closer than about three particle diameters41. Triggered by the experiment findings, we have recently presented a rigorous analytical model that predicts the critical Shields number in the creeping flow limit40. The model covers the onset of motion from highly exposed to hidden beads.
The first part of this manuscript deals with the description of the experimental procedure used in previous studies at shear Reynolds number, Re*, lower than 1. The laminar flow is induced with a rotational rheometer with a parallel configuration. In this low Reynolds number limit, the particle is not supposed to experience any velocity fluctuation20 and the system matches the so-called hydraulically smooth flow where the particle is submerged within the viscous sublayer.
Once incipient motion at laminar flow is established, the role of turbulence can become clearer. Motivated by this idea, we introduce a novel experimental procedure in the second part of the protocol. Using a Göttingen low-speed wind tunnel with open jet test section, the critical Shields number can be determined in a wide range of Re* including the hydraulically transitional flow and the turbulent regime. The experimental results can provide important insight about how forces and torques act on a particle due to the turbulent flow depending on the substrate geometry. Besides, these results can be used as a benchmark for more sophisticated models at high Re* in a similar way that past work in laminar flow has been used to feed semi probabilistic models52 or to validate recent numerical models53. We present some representative examples of applications at Re* ranging from 40 to 150.
The incipient criterion is established as the motion of the single particle from its initial equilibrium position to the next one. Image processing is used to determine the mode of onset of motion, i.e. rolling, sliding, lifting39,41. For that purpose, the angle of rotation of mobile spheres that were manually marked is detected. The algorithm tracks the position of the marks and compares it with the center of the sphere. A preliminary set of experiments was conducted in both experimental set-ups to clarify that the critical Shields number remains independent of finite size effects of the set-up and relative flow submergence. The experimental methods are thus designed to exclude any other parameter dependent on the critical Shields number beyond Re* and geometrical properties of the sediment bed. The Re* is varied using different fluid-particle combinations. The critical Shields number is characterized as a function of the burial degree,  , defined by Martino et al.37 as
, defined by Martino et al.37 as 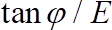 where
where  is the angle of repose, i.e. the critical angle at which motion occurs54, and
is the angle of repose, i.e. the critical angle at which motion occurs54, and  is the exposure degree, defined as the ratio between the cross-sectional area effectively exposed to the flow to the total cross-sectional area of the mobile bead.
is the exposure degree, defined as the ratio between the cross-sectional area effectively exposed to the flow to the total cross-sectional area of the mobile bead.
Access restricted. Please log in or start a trial to view this content.
Protokół
1. Incipient Particle Motion in the Creeping Flow Limit.
NOTE: The measurements are conducted in a rotational rheometer that has been modified for this specific application.
- Preparing the Rheometer.
- Connect the air supply to the rheometer in order to avoid damaging the air bearings. Open the valve besides the air filters until a pressure of approximately 5 bars in the system is achieved.
- Connect the fluid circulator to the measuring plate. Ensure that the hoses of the Peltier element are connected to the rheometer. Switch on the fluid circulator and set the desired temperature (20 °C).
- Mount the customized container containing the regular substrate on the rheometer.
- Take the regular substrate out of the container and clean the surface carefully with distilled water. Dry the surface with a lens cleaning cloth and remove possible residual dust with a blower.
NOTE: The regular substrates are monolayers of 15 x 15 mm2 built from spherical soda-lime glass beads of (405.9 ± 8.7) µm. - Using 0.4 mm thickness double-sided tape, fix the regular substrate into the container ensuring that the substrate center is at a distance of 21 mm from the turning axis.
- Place the customized adapter on the rheometer plate.
- Mount the customized circular container into the plate ensuring that the flat front section is facing the imaging system designed for side recording.
NOTE: Ensure that the container is completely horizontal with the water level (0.6 mm/m). For that purpose, place the water level on the container parallel to the back of the device and level it with the rheometer adjustable feet. Repeat the procedure turning the water level by 90 degrees.
- Take the regular substrate out of the container and clean the surface carefully with distilled water. Dry the surface with a lens cleaning cloth and remove possible residual dust with a blower.
- Switch on the rheometer. Wait until the boot procedure is finished and the status "ok" appears on the device screen.
- Start the computer and the rheometer software. Initialize the rheometer and set the temperature control from the control panel of the software to the desired value (20 °C).
- Mount the customized measuring system. Set-up the zero gap from the software.
NOTE: Before setting the zero gap, ensure that there are no mobile beads on the substrate and that the substrate borders are not bent. An error in setting the zero-gap will lead to a systematic error in the calculation of the shear rate and therefore in the subsequent measurement of the critical Shields number. An absolute uncertainty of 0.05 mm is assumed in the gap width when calculating the critical Shields number. - Lift the measuring plate to 30 mm and remove it.
- Fill the container with approximately 70 mL of 100 mPa·s silicon oil. Ensure that the level of the fluid in the container remains above 2 mm. The silicon oil should not cover the upper part of the transparent plate. Wait approximately 15-20 min for the thermal equilibrium. During that time, adjust the imaging systems (see step 2 from the protocol).
NOTE: The temperature that is fixed to (295.15 ± 0.5) K here, is controlled with a Peltier element connected to the rheometer and measured with an external thermometer. Fluctuations of less than 0.5 K are observed during the experiments.
- Adjusting the imaging system.
- Switch on the 300 W Arc Xenon Lamp. Adjust the flexible light guide to illuminate the bead from the side through the transparent walls of the container.
- Adjust the LED light intensity to avoid strong light reflection on the substrate.
- Adjust the imaging system designed for recording the particle motion from the top through the transparent measuring plate.
- Start-up the imaging software from the computer and choose the monochrome profile from the start dialog.
- Open the 768 x 576 CMOS camera of the imaging system installed on the top of the container. Start up the live video.
- Adjust the horizontal positioning stage until the reference position that has been previously marked in the center of the substrate appears in the center of the image.
- Adjust the vertical positioning stage to focus on the substrate.
- Place carefully a marked soda-lime glass sphere of (405.9 ± 8.7) µm.
- Ensure that at least one of the marks is placed at a distance of approximately 75% of the bead radius or larger from the axis of rotation. If this is not the case, move manually the measuring plate to achieve the motion of the bead to the next equilibrium position (see Figure 2(a) as a reference).
NOTE: To ensure proper monitoring during motion the mobile beads are marked with several spots separated by about 45° (see Figure 3(a)). The code includes a simple control flow statement to minimize mark misassignment in order to calculate the angle of rotation. For further details, we refer to Agudo et al. 201739. - Open the dialog box for setting the camera parameters and adjust the frame rate to 30 fps. Adjust the exposure time to ensure that the marks are properly distinguished from the bead perimeter.
NOTE: The soda-lime glass sphere submerged into a silicon oil of 100 mPa·s requires about 4 seconds to move from its initial position to the watershed to the neighboring equilibrium position. Hence, a framerate of 30 fps permits an uncertainty of less than 1%.
- Mount the measuring plate to the rheometer.
- Set the measuring distance to 2 mm.
NOTE: The focus of the top camera must be slightly readjusted due to the presence of the Plexiglas plate. - Adjust the imaging system designed for recording the particle motion from the side through the transparent microscope slide.
- Open the 4912 x 3684 CMOS camera of the imaging system installed at the front of the container and start up the live video.
- Adjust the vertical and the horizontal positioning stage placed parallel to the rheometer until the marked bead appears in the center of the image.
- Adjust the modular zoom lens until the field of view includes the upper surface of the substrate, the bead, and the bottom part of the measuring disk.
- Adjust the horizontal positioning stage placed perpendicular to the rheometer to focus on the bead.
- Open the dialog box for setting the camera parameters and adjust the frame rate to 30 fps.
- Determine the critical rotating speed for the onset of motion.
- Increase linearly the rotational speed, n, from 0.02 to 0.05 revolutions per second in small increments of 0.00025 revolutions per second using the rheometer software.
- In the measurement window, double-click the cell for the control type and edit the range of the speed from 0.02 to 0.05 revolutions per second.
- Double-click the time setting and enter the number of measurement points, 60, and the duration of each measurement, 5 s.
- Set a table representing the rotational speed as a function of time.
- Open the live video from the top and side cameras. Start recording a video-sequence from both cameras using the imaging software.
- Start the measurement using the rheometer software.
NOTE: A preliminary experiment with a larger step size is recommended prior to step 1.3.1.1 in order to roughly estimate the speed range at which the incipient motion will happen. At a distance of 21 mm from the turning axis and using the silicone oil of 100 mPa·s, for instance, the glass bead moves at rotating speeds of approximately 0.035 revolutions per second. Hence, a range from 0.02 to 0.05 revolutions per second seems appropriate for the experiment. - Look carefully at the live video from the top or from the side camera and stop the measurement when the bead displaces from its equilibrium position. Note the speed at which the bead crosses the separatrix to the neighboring equilibrium position. The noted rotating speed represents the critical rotating speed, nC. Stop the video-sequences.
NOTE: Ensure that the step size is small enough that the increase of speed during the time interval that the bead requires moving from its initial position to the neighboring one does not involve more than 1% of the critical value. - Place the bead back to its original position. This can be done by moving manually the rotating plate until the bead displaces one position back. Repeat the experiment five times noting the mean critical speed and the standard deviation.
- Repeat the steps 1.3.1 to 1.3.5 with a different marked bead in 2 adjacent positions to the center of the substrate.
- Increase linearly the rotational speed, n, from 0.02 to 0.05 revolutions per second in small increments of 0.00025 revolutions per second using the rheometer software.
- Analyzing the data.
- Determine the mode of motion: analyze the sequence of images previously recorded from the top or from the side with the algorithm as described in Agudo et al. 201739.
- Determine the critical Shields number and the shear Reynolds number.
- Obtain the critical Shields number from the following equation40
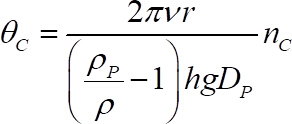 (1)
(1)
where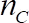 has been obtained from step 1.3.4,
has been obtained from step 1.3.4,  is the kinematic viscosity,
is the kinematic viscosity,  and
and  are particle and liquid densities, respectively,
are particle and liquid densities, respectively, 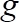 is the acceleration of gravity and
is the acceleration of gravity and 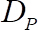 is the mobile bead diameter, all of them known.
is the mobile bead diameter, all of them known.  is the gap width, defined as the distance from the top of the substrate spheres to the measuring plate, i.e. 2 mm and r is the radial distance of the particle from the turning axis, i.e. 21 mm.
is the gap width, defined as the distance from the top of the substrate spheres to the measuring plate, i.e. 2 mm and r is the radial distance of the particle from the turning axis, i.e. 21 mm. - Obtain the shear Reynolds number, Re* based on the shear velocity, from the following equations:
 (2)
(2)
- Obtain the critical Shields number from the following equation40
- Repeat the procedure from 1.1.3 to 1.4.2 using a different regular substrate.
- Use different bead densities and different fluid viscosities in order to cover a broad range of the Re* from creeping flow conditions up to 1.
2. Incipient Particle Motion at the Hydraulically Transitional and Rough Turbulent Regime.
NOTE: The measurements are conducted in a customized low-speed Wind-tunnel with open jet test section, Göttingen type.
- Preparing the imaging system.
- Fix the quadratic substrate in the middle of the test section.
- Place a 5 mm alumina bead previously marked at the desired initial position (110 mm from the leading edge and 95 mm from the side edge).
- Connect the high-speed camera coupled to the macro lens to the computer and switch it on. Adjust the macro lens until the target bead is clear in the image.
- Initiate the imaging software on the computer. Activate "Live Camera", and set the "Sample rate" to 1000 fps.
- Switch on the LED light source and adjust the intensity as well as the focus of the camera to achieve a clear image of the particle and its marks.
NOTE: Ensure that at least one of the marks is placed at a distance of approximately 75% of the bead radius or larger from the axis of rotation (see Figure 3(a) as a reference).
- Determining the critical fan speed for the onset of motion.
- Set the fan speed well below the critical value (approximately 1400 rpm for the 5 mm alumina bead).
- Start the recording by pressing the trigger on the imaging software.
- Increase the speed in steps of approximately 4 to 6 rpm every 10 s until incipient motion occurs.
- Note the critical speed value at which incipient motion occurs and stop the video sequence.
- Place a new marked bead at the same initial position and repeat the procedure from 2.2.1 to 2.2.4 ten times. Note the critical speed for each measurement.
- Repeat the procedure from 2.2.1 to 2.2.5 at the same distance from the leading edge but at 65 and 125 mm from the side edge, respectively. Note the critical speed for each measurement.
- Preparing the constant temperature hot-wire anemometer (CTA).
- Set the CTA control function to stand by and the decade resistance to 00.00. Switch on the main power and wait for approximately 15-20 min to warm up.
- Plug the shorting probe and switch the CTA control function to resistance measurement. Adjust the zero Ohms until the needle is placed in the red mark and switch back the control function to standby.
- Replace the shorting probe by the miniature hot-wire probe. Switch the CTA control function to resistance measurement. Adjust the resistance switches until the needle is placed in the red mark.
NOTE: The measured resistance corresponds to the cold resistance of the miniature probe. The measured value should be in agreement with the value provided by the manufacturer (3.32 Ω). - Switch the CTA function to stand by and adjust the resistance decade to 5.5 Ω to achieve an overheat ratio of about 65%.
- Measure the frequency response of the CTA at the mean critical speed (step 2.2.4).
- Switch on the fan and set the rotational speed of the fan to the critical value, about 1400 rpm. Switch on the oscilloscope.
- Switch the square wave generator of the CTA on.
- Initiate the oscilloscope software on the computer and open the CSV module to enable the data recording. Choose the channel (CH1) and save the recording data i.e. time and voltage, under the desired file name. Wait until the measurements finish (about 3 min).
NOTE: The cut-off frequency is calculated from the response time at which the voltage dropped to a level of - 3db (see Figure 4(a)). - Switch the square wave generator off and set the CTA function to standby.
- Calibrating the CTA.
- Switch the CTA function to operate. Ensure that the probe is adjusted to a sufficient height away from the plate so that it is located in the free stream zone.
- Set the fan rotational speed to 200 rpm. Measure the streamwise velocity in the free stream zone using the impeller anemometer and read the voltage on the oscilloscope.
- Repeat step 2.4.2 for different rotational speeds with a fixed increment of 50 rpm up to about 1450 rpm (a total of 26 reads).
- Establish a correlation between the rpm and the measured free-stream streamwise velocity,
 . Obtain the critical velocity,
. Obtain the critical velocity,  , corresponding to the critical rotational speed for each of the measurements performed from steps 2.2.5 to 2.2.6. Calculate the mean critical free-stream velocity,
, corresponding to the critical rotational speed for each of the measurements performed from steps 2.2.5 to 2.2.6. Calculate the mean critical free-stream velocity,  and the standard deviation of the measurements.
and the standard deviation of the measurements. - Establish a correlation between the velocity and the voltage according to a third-degree polynomial fit:
 (3)
(3)
Here, is the streamwise velocity measured in m/s,
is the streamwise velocity measured in m/s,  is the voltage measured in Volt (V), and
is the voltage measured in Volt (V), and 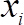 are the fit coefficients. The calibration curves are shown in Figure 4(b) before and after the measurements of the velocity profile.
are the fit coefficients. The calibration curves are shown in Figure 4(b) before and after the measurements of the velocity profile.
- Measuring the streamwise velocity with the wall-normal position at critical conditions.
- Remove the marked bead from the substrate.
- Adjust the handwheel of the horizontal positioning stage until the hot wire probe is placed at the desired initial position (110 mm from the leading edge and 95 mm from the side edge).
- Adjust carefully the handwheel of the vertical positioning stage until the probe is placed as close as possible to the substrate surface. See through the camera coupled to the macro lens to ensure that the wire does not touch the substrate surface. Set the zero value in the digital level indicator at that position.
Caution: The hot wire is very sensitive and if it touches the surface it will break. For sake of security, we place the probe at a distance of 0.05 mm above the top of the substrate sphere (see Figure 1(e) as a reference). This represents a normalized wall-normal component where
where 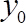 is the starting measuring value,
is the starting measuring value, 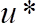 is the shear velocity and
is the shear velocity and  is the kinematic viscosity of air at operating temperature. Note that the starting value is below
is the kinematic viscosity of air at operating temperature. Note that the starting value is below  where the viscosity is dominant55.
where the viscosity is dominant55. - Set the fan rotational speed to the mean rotational speed at which the incipient motion occurs, see step 2.2.4. The free-stream velocity thus corresponds to
 .
. - Adjust the sampling rate to 1 kSa and the number of samples to 6000 on the oscilloscope (total sampling time of 6 s). Choose the channel (CH1) and start the measurement. Save the recording data under the desired file name. Wait until the measurements finish (about 3 min).
- Increase the wall-normal position of the probe by an increment of 0.01 mm up to 0.4 mm, and by an increment of 0.1 mm up to the height of 10 mm. This corresponds to a total of 137 points for the velocity profile curve. Save the recorded data for each height.
- Analyzing the data.
- Calculate the mean streamwise velocity and the turbulent intensity for each wall-normal position.
- Run the self-developed algorithm to evaluate the statistical quantities. Open the script and select the folder containing the calibration curve and the stored data for each of the measured height.
NOTE: The script computes first the fit coefficients from the calibration curve as shown in Eq. 3. For each height, it calculates the instantaneous streamwise velocity,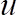 by using Eq. 3 and computes the integral time scale by the autocorrelation method56. Thereafter, it computes the time average,
by using Eq. 3 and computes the integral time scale by the autocorrelation method56. Thereafter, it computes the time average,  and the root square velocity,
and the root square velocity, 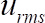 , for samples that are separated by two times the integral time necessary for the time-averaged analysis.
, for samples that are separated by two times the integral time necessary for the time-averaged analysis. - Plot the dimensionless vertical position,
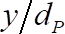 against the dimensionless streamwise time average velocity
against the dimensionless streamwise time average velocity 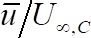 , where
, where 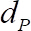 is the diameter of the substrate spheres. Plot
is the diameter of the substrate spheres. Plot 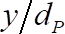 against the dimensionless root square velocity
against the dimensionless root square velocity  . Figure 4(c)-(d) depicts the results for the case of the 5 mm alumina bead.
. Figure 4(c)-(d) depicts the results for the case of the 5 mm alumina bead.
- Run the self-developed algorithm to evaluate the statistical quantities. Open the script and select the folder containing the calibration curve and the stored data for each of the measured height.
- Calculate the shear velocity from the experimental data.
- Fit the dimensionless time average velocity with the logarithmic velocity distribution57
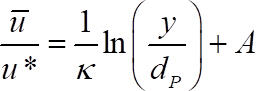 (5)
(5)
where is the shear velocity,
is the shear velocity, 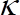 is the von Kármán's constant and
is the von Kármán's constant and  is a constant that depends on the shear Reynolds number26. The solid line in Figure 4(c) is a logarithmic fit to the time average velocity.
is a constant that depends on the shear Reynolds number26. The solid line in Figure 4(c) is a logarithmic fit to the time average velocity.
NOTE: From the fit to the experimental data, it can be shown that the shear velocity, is given by:
is given by:
 (6)
(6)
where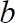 is the logarithmic fit coefficient and
is the logarithmic fit coefficient and  20.
20.
The viscous sublayer, remains above the top of the substrate spheres in our experiments. In the most rigorous scenario, Eq. 5 should be replaced by the modified velocity law presented by Rotta20,58.
remains above the top of the substrate spheres in our experiments. In the most rigorous scenario, Eq. 5 should be replaced by the modified velocity law presented by Rotta20,58.
 (7)
(7)
where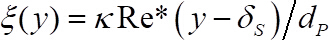 and
and 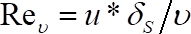 .
.  is the viscous sublayer thickness that can be approximately calculated by
is the viscous sublayer thickness that can be approximately calculated by  55.
55.
The algorithm computes directly the shear velocity from the fit of experimental data to Eq. 5 and Eq. 7. The blue symbols in Figure 4(c) represent the fit to the experimental data according to Eq. 7.
At Re* above 70, represents up to 5% of the mobile bead diameter, and using a fit from Eq. 5 or Eq. 7 involves a variation on
represents up to 5% of the mobile bead diameter, and using a fit from Eq. 5 or Eq. 7 involves a variation on 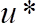 within the adopted range of uncertainty. Compare solid line and blue symbols in Figure 4(c) at a Re* of about 87.5.
within the adopted range of uncertainty. Compare solid line and blue symbols in Figure 4(c) at a Re* of about 87.5.
- Fit the dimensionless time average velocity with the logarithmic velocity distribution57
- Determine the mode of motion: analyze the sequence of images previously recorded from the side with the algorithm as described in Agudo et al. 201739.
- Determine the critical Shields number and the shear Reynolds number.
- Obtain the critical Shields number from the following equation22
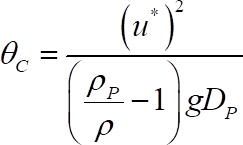 (8)
(8)
where has been obtained from step 10.2,
has been obtained from step 10.2,  and
and  are particle and fluid densities, respectively,
are particle and fluid densities, respectively, 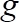 is the acceleration of gravity and
is the acceleration of gravity and 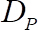 is the mobile bead diameter, all of them known.
is the mobile bead diameter, all of them known. - Obtain the particle Reynolds number, Re*, from the following equations:
 (9)
(9) - Repeat the procedure for measuring the velocity profile as a function of the wall-normal coordinate, step 2.5, at the same distance from the leading edge but at 65 and 125 mm in the width direction, respectively.
- Repeat the procedure from 2.1 to 2.6.4.3 using different bead sizes and regular substrates.
- Obtain the critical Shields number from the following equation22
- Calculate the mean streamwise velocity and the turbulent intensity for each wall-normal position.
Access restricted. Please log in or start a trial to view this content.
Wyniki
Figure 1(a) represents a sketch of the experimental set-up used to characterize the critical Shields number in the creeping flow limit, Section 1 of the protocol. The measurements are conducted in a rotational rheometer that was modified for this specific application. A transparent Plexiglas plate of 70 mm in diameter was carefully fixed to a parallel plate of 25 mm in diameter. The inertia of the measuring system was therefore readjusted bef...
Access restricted. Please log in or start a trial to view this content.
Dyskusje
We present two different experimental methods for characterizing the incipient particle motion as a function of the sediment bed geometry. For that purpose, we use a monolayer of spheres regularly arranged according to a triangular or quadratic symmetry in such a way that the geometrical parameter simplifies to a single geometry. In the creeping flow limit, we describe the experimental method using a rotational rotameter to induce the laminar shear flow as in previous studies39,
Access restricted. Please log in or start a trial to view this content.
Ujawnienia
The authors have nothing to disclose
Podziękowania
The authors are thankful to unknown referees for valuable advice and to Sukyung Choi, Byeongwoo Ko and Baekkyoung Shin for the collaboration in setting up the experiments. This work was supported by the Brain Busan 21 Project in 2017.
Access restricted. Please log in or start a trial to view this content.
Materiały
| Name | Company | Catalog Number | Comments |
| MCR 302 Rotational Rheometer | Anton Paar | Induction of shear laminar flow | |
| Measuring Plate PP25 | Anton Paar | Induction of shear laminar flow | |
| Peltier System P-PTD 200 | Anton Paar | Keep temperature of silicon oils constant in the system at laminar flow | |
| Silicone oils with viscosities of approx. 10 and 100 mPas | Basildon Chemicals | Fluid used to induced the shear in the particles | |
| Soda-lime glass beads of (405.9 ± 8.7) μm | The Technical Glass Company | Construction of the regular substrates for laminar flow conditions | |
| Opto Zoom 70 Module 0.3x-2.2x | WEISS IMAGING AND SOLUTIONS GmbH | Imaging system for recording the bead motion in the rheometer | |
| 2 x TV-Tube 1.0x, D=35 mm, L=146.5 mm | WEISS IMAGING AND SOLUTIONS GmbH | Imaging system for recording the bead motion in the rheometer | |
| UI-1220SE CMOS Camera | IDS Imaging Development Systems GmbH | Imaging system for recording the bead motion in the rheometer | |
| UI-3590CP CMOS Camera | IDS Imaging Development Systems GmbH | Imaging system for recording the bead motion in the rheometer | |
| Volpi IntraLED 3 - LED light source | Volpi USA | Imaging system for recording the bead motion in the rheometer | |
| Active light guide diameter 5mm | Volpi USA | Imaging system for recording the bead motion in the rheometer | |
| 300 Watt Xenon Arc Lamp | Newport Corporation | Imaging system for recording the bead motion in the rheometer | |
| Wind-tunnel with open jet test section, Göttingen type | Tintschl BioEnergie und Strömungstechnik AG | Induction of turbulent flow | |
| Glass spheres of (2.00 ± 0.10) mm | Gloches South Korea | Construction of the regular substrates for turbulent flow conditions | |
| Alumina spheres of (5.00 ± 0.25) mm | Gloches South Korea | Targeted bead for experiments | |
| CTA Anemometer DISA 55M01 | Disa Elektronik A/S | Measurement of flow velocity in the wind tunnel | |
| Miniaure Wire Probe Type 55P15 | Dantec Dynamics | Measurement of flow velocity in the wind tunnel | |
| HMO2022 Digital Oscilloscope, 2 Analogue. Ch., 200MHz | Rohde & Schwarz | Measurement of flow velocity in the wind tunnel | |
| Phantom Miro eX1 High-speed Camera | Vision Research IncVis | Imaging system for recording the bead motion in the wind-tunnel | |
| Canon ef 180mm f/3.5 l usm macro lens | Canon | Imaging system for recording the bead motion in the wind-tunnel | |
| Table LED Lamp | Gloches South Korea | Imaging system for recording the bead motion in the wind-tunnel |
Odniesienia
- Groh, C., Wierschem, A., Aksel, N., Rehberg, I., Kruelle, C. A. Barchan dunes in two dimensions: Experimental tests for minimal models. Phys. Rev. E. 78, 021304(2008).
- Wierschem, A., Groh, C., Rehberg, I., Aksel, N., Kruelle, C. Ripple formation in weakly turbulent flow. Eur. Phys. J. E. 25, 213-221 (2008).
- Herrmann, H. Dune Formation in Traffic and Granular Flow. , Springer. Berlin. (2007).
- Stevanovic, V. D., et al. Analysis of transient ash pneumatic conveying over long distance and prediction of transport capacity. Powder Technol. 254, 281-290 (2014).
- Fan, F. -G., Soltani, M., Ahmadi, G., Hart, S. C. Flow-induced resuspension of rigid-link fibers from surfaces. Aerosol. Sci. Tech. 27, 97-115 (1997).
- Burdick, G., Berman, N., Beaudoin, S. Hydrodynamic particle removal from surfaces. Thin Solid Films. , 116-123 (2005).
- Chang, Y. Laboratory investigation of flume traction and transportation. Proceedings of the American Society of Civil Engineers. , 1701-1740 (1939).
- Paintal, A. A stochastic model of bed load transport. J. Hydraul. Res. 9, 527-554 (1971).
- Mantz, P. A. Incipient transport of fine grains and flakes by fluids-extended shield diagram. J. Hydr. Eng. Div.-Asce. 103, (1977).
- Yalin, M. S., Karahan, E. Inception of sediment transport. J. Hydr. Eng. Div.-Asce. 105, 1433(1979).
- Kuhnle, R. A. Incipient motion of sand-gravel sediment mixtures. J. Hydraul. Eng. 119, 1400-1415 (1993).
- Marsh, N. A., Western, A. W., Grayson, R. B. Comparison of methods for predicting incipient motion for sand beds. J. Hydraul. Eng. 130, 616-621 (2004).
- Vollmer, S., Kleinhans, M. G. Predicting incipient motion, including the effect of turbulent pressure fluctuations in the bed. Water Resour. Res. 43, (2007).
- Valyrakis, M., Diplas, P., Dancey, C. L., Greer, K., Celik, A. O. Role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res.-Earth. 115, (2010).
- Dey, S., Ali, S. Z. Stochastic mechanics of loose boundary particle transport in turbulent flow. Phys. Fluids. 29, 055103(2017).
- Wiberg, P. L., Smith, J. D. Calculations of the critical shear stress for motion of uniform and heterogeneous sediments. Water Resour. Res. 23, 1471-1480 (1987).
- Ling, C. -H. Criteria for incipient motion of spherical sediment particles. J. Hydraul. Eng. 121, 472-478 (1995).
- Dey, S. Sediment threshold. Appl. Math. Model. 23, 399-417 (1999).
- Bravo, R., Ortiz, P., Pérez-Aparicio, J. Incipient sediment transport for non-cohesive landforms by the discrete element method (DEM). Appl. Math. Model. 38, 1326-1337 (2014).
- Ali, S. Z., Dey, S. Hydrodynamics of sediment threshold. Phys. Fluids. 28, 075103(2016).
- Yalin, M. S. Mechanics of sediment transport. , Pergamon Press. California. (1977).
- Graf, W. H., Sueska, L. Sediment transport in steep channels. Journal of Hydroscience and Hydraulic Engineering. 5, 233-255 (1987).
- Recking, A. An experimental study of grain sorting effects on bedload. , Lyon. Doctor in Sciences thesis, Institut National des Sciences Appliques de Lyon (2006).
- Roušar, L., Zachoval, Z., Julien, P. Incipient motion of coarse uniform gravel. J. Hydraul. Res. 54, 615-630 (2016).
- Miller, R. L., Byrne, R. J. The angle of repose for a single grain on a fixed rough bed. Sedimentology. 6, 303-314 (1966).
- Fenton, J., Abbott, J. Initial movement of grains on a stream bed: the effect of relative protrusion. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 352, 523-537 (1977).
- Kirchner, J. W., Dietrich, W. E., Iseya, F., Ikeda, H. The variability of critical shear stress, friction angle, and grain protrusion in water-worked sediments. Sedimentology. 37, 647-672 (1990).
- Armanini, A., Gregoretti, C. Incipient sediment motion at high slopes in uniform flow condition. Water Resour. Res. 41, (2005).
- Chin, C., Chiew, Y. Effect of bed surface structure on spherical particle stability. J. Waterw. Port Coast. 119, 231-242 (1993).
- Whitehouse, R., Hardisty, J. Experimental assessment of two theories for the effect of bedslope on the threshold of bedload transport. Mar. Geol. 79, 135-139 (1988).
- Buffington, J. M., Montgomery, D. R. A systematic analysis of eight decades of incipient motion studies, with special reference to gravel-bedded rivers. Water Resour. Res. 33, 1993-2029 (1997).
- Charru, F., Mouilleron, H., Eiff, O. Erosion and deposition of particles on a bed sheared by a viscous flow. J. Fluid Mech. 519, 55-80 (2004).
- Loiseleux, T., Gondret, P., Rabaud, M., Doppler, D. Onset of erosion and avalanche for an inclined granular bed sheared by a continuous laminar flow. Phys. Fluids. 17, 103304(2005).
- Charru, F., Larrieu, E., Dupont, J. -B., Zenit, R. Motion of a particle near a rough wall in a viscous shear flow. J. Fluid Mech. 570, 431-453 (2007).
- Ouriemi, M., Aussillous, P., Medale, M., Peysson, Y., Guazzelli, É Determination of the critical Shields number for particle erosion in laminar flow. Phys. Fluids. 19, 061706(2007).
- Lobkovsky, A. E., Orpe, A. V., Molloy, R., Kudrolli, A., Rothman, D. H. Erosion of a granular bed driven by laminar fluid flow. J. Fluid Mech. 605, 47-58 (2008).
- Martino, R., Paterson, A., Piva, M. Onset of motion of a partly hidden cylinder in a laminar shear flow. Phys. Rev. E. 79, 036315(2009).
- Agudo, J., Wierschem, A. Incipient motion of a single particle on regular substrates in laminar shear flow. Phys. Fluids. 24, 093302(2012).
- Agudo, J., et al. Detection of particle motion using image processing with particular emphasis on rolling motion. Rev. Sci. Instrum. 88, 051805(2017).
- Agudo, J., et al. Shear-induced incipient motion of a single sphere on uniform substrates at low particle Reynolds numbers. J. Fluid Mech. 825, 284-314 (2017).
- Agudo, J., Dasilva, S., Wierschem, A. How do neighbors affect incipient particle motion in laminar shear flow? Phys. Fluids. 26, 053303(2014).
- Seizilles, G., Lajeunesse, E., Devauchelle, O., Bak, M. Cross-stream diffusion in bedload transport. Phys. Fluids. 26, 013302(2014).
- Seizilles, G., Devauchelle, O., Lajeunesse, E., Métivier, F. Width of laminar laboratory rivers. Phys. Rev. E. 87, 052204(2013).
- Hong, A., Tao, M., Kudrolli, A. Onset of erosion of a granular bed in a channel driven by fluid flow. Phys. Fluids. 27, 013301(2015).
- Derksen, J., Larsen, R. Drag and lift forces on random assemblies of wall-attached spheres in low-Reynolds-number shear flow. J. Fluid Mech. 673, 548-573 (2011).
- Happel, J., Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media. , Martinuis Nijhoff. The Hague. (1983).
- Lajeunesse, E., et al. Fluvial and submarine morphodynamics of laminar and near-laminar flows: A synthesis. Sedimentology. 57, 1-26 (2010).
- Aussillous, P., Chauchat, J., Pailha, M., Médale, M., Guazzelli, É Investigation of the mobile granular layer in bedload transport by laminar shearing flows. J. Fluid Mech. 736, 594-615 (2013).
- Thompson, J. A., Bau, H. H. Microfluidic, bead-based assay: Theory and experiments. J. Chromatogr. B. 878, 228-236 (2010).
- Sawetzki, T., Rahmouni, S., Bechinger, C., Marr, D. W. In situ assembly of linked geometrically coupled microdevices. Proceedings of the National Academy of Sciences. 105, 20141-20145 (2008).
- Amini, H., Sollier, E., Weaver, W. M., Di Carlo, D. Intrinsic particle-induced lateral transport in microchannels. Proceedings of the National Academy of Sciences. 109, 11593-11598 (2012).
- Soepyan, F. B., et al. Threshold velocity to initiate particle motion in horizontal and near-horizontal conduits. Powder Technol. 292, 272-289 (2016).
- Deskos, G., Diplas, P. Incipient motion of a non-cohesive particle under Stokes flow conditions. International Journal of Multiphase Flow. , (2017).
- Julien, P. Y. Erosion and sedimentation. , Cambridge University Press. Cambridge. (2010).
- Jimenez, J. Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173-196 (2004).
- O’neill, P., Nicolaides, D., Honnery, D., Soria, J. 15th Australasian Fluid Mechanics Conference. , The University of Sydney. 1-4 (2006).
- Schlichting, H. Boundary-Layer Theory. , McGraw-Hill. New York. (1979).
- Rotta, J. Das in wandnähe gültige Geschwindigkeitsgesetz turbulenter Strömungen. Arch. Appl. Mech. 18, 277-280 (1950).
- Schlichting, H., Gersten, K., Krause, E., Oertel, H. Boundary-layer theory. 7, Springer. (1955).
- Bruun, H. H. Hot-wire anemometry-principles and signal analysis. , Oxford: University Express. Oxford. (1995).
- Fan, D., Cheng, X., Wong, C. W., Li, J. -D. Optimization and Determination of the Frequency Response of Constant-Temperature Hot-Wire Anemometers. AIAA J. , 1-7 (2017).
- Valyrakis, M., Diplas, P., Dancey, C. L. Entrainment of coarse particles in turbulent flows: An energy approach. J. Geophys. Res.-Earth. 118, 42-53 (2013).
- Valyrakis, M., Diplas, P., Dancey, C. L. Entrainment of coarse grains in turbulent flows: An extreme value theory approach. Water Resour. Res. 47, (2011).
- Dey, S., Das, R., Gaudio, R., Bose, S. Turbulence in mobile-bed streams. Acta Geophys. 60, 1547-1588 (2012).
- Wu, F. -C., Chou, Y. -J. Rolling and lifting probabilities for sediment entrainment. J. Hydraul. Res. 129, 110-119 (2003).
- Leighton, D., Acrivos, A. The lift on a small sphere touching a plane in the presence of a simple shear flow. Z. Angew. Math. Phys. 36, 174-178 (1985).
- Tuyen, N. B., Cheng, N. -S. A single-camera technique for simultaneous measurement of large solid particles transported in rapid shallow channel flows. Exp. Fluids. 53, 1269-1287 (2012).
- Gollin, D., Bowman, E., Shepley, P. Methods for the physical measurement of collisional particle flows. IOP Conference Series: Earth and Environmental Science. 26, 012017(2015).
- Amon, A., et al. Focus on Imaging Methods in Granular Physics. Rev. Sci. Instrum. 88, (2017).
- Mouilleron, H., Charru, F., Eiff, O. Inside the moving layer of a sheared granular bed. J. Fluid Mech. 628, 229-239 (2009).
- Diplas, P., et al. The role of impulse on the initiation of particle movement under turbulent flow conditions. Science. 322, 717-720 (2008).
- Coleman, N. L. A theoretical and experimental study of drag and lift forces acting on a sphere resting on a hypothetical streambed. International Association for Hydraulic Research, 12th Congress, proceedings. 3, 185-192 (1967).
- El-Gabry, L. A., Thurman, D. R., Poinsatte, P. E. Procedure for determining turbulence length scales using hotwire anemometry. , NASA Technical Reports NASA/TM-2014-218403 (2014).
- Roach, P. The generation of nearly isotropic turbulence by means of grids. Int. J. Heat Fluid Fl. 8, 82-92 (1987).
Access restricted. Please log in or start a trial to view this content.
Przedruki i uprawnienia
Zapytaj o uprawnienia na użycie tekstu lub obrazów z tego artykułu JoVE
Zapytaj o uprawnieniaThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Wszelkie prawa zastrzeżone