É necessária uma assinatura da JoVE para visualizar este conteúdo. Faça login ou comece sua avaliação gratuita.
Method Article
Visualmente, com base em caracterização do movimento de partículas incipiente em substratos Regular: de Laminar para turbulentas condições
Neste Artigo
Resumo
São apresentados dois métodos diferentes para caracterizar o movimento de partículas incipiente de uma única pérola como uma função da geometria de cama de sedimentos de laminar para fluxo turbulento.
Resumo
Dois diferentes métodos experimentais para a determinação do limiar do movimento de partículas em função das Propriedades geométricas da cama de laminar para fluxo turbulento condições são apresentados. Para esse efeito, o incipiente movimento de uma única conta é estudado em substratos regulares que consistem em uma monocamada de esferas fixas de tamanho uniforme regularmente organizados em simetrias triangulares e quadráticas. O limiar é caracterizado pelo crítico número escudos. O critério para o início do movimento é definido como o deslocamento da posição original de equilíbrio para o vizinho. O deslocamento e o modo de movimento são identificados com um sistema de imagem. O fluxo laminar é induzido usando um rheometer rotacional com uma configuração de disco paralelo. O número de Reynolds de cisalhamento permanece inferior a 1. O fluxo turbulento é induzido em um túnel de vento de baixa velocidade com seção de teste do jato aberto. A velocidade do ar é regulada com um variador de frequência no ventilador ventilador. O perfil de velocidade é medido com uma sonda de fio quente conectada a um anemômetro de filme quente. O número de Reynolds de cisalhamento variam entre 40 e 150. A lei de velocidade logarítmica e a lei de parede modificado apresentado por Rotta são usados para inferir a velocidade de cisalhamento a partir dos dados experimentais. O último é de especial interesse quando o grânulo móvel fica parcialmente exposto ao fluxo turbulento no regime transitório hidraulicamente fluxo so-called. A tensão de cisalhamento é estimado no início do movimento. Alguns resultados ilustrativos, mostrando o forte impacto do ângulo de repouso e a exposição do cordão para cortar o fluxo de são representados em ambos os regimes.
Introdução
Movimento de partícula incipiente é encontrado em uma ampla gama de processos industriais e naturais. Ambientais são exemplos o processo inicial de sedimento transporte no rio e oceanos, erosão de cama ou formação de dunas, entre outros, 1,2,3. Pneumático, transportando4, remoção de poluentes ou limpeza de superfícies5,6 são aplicações industriais típicas, envolvendo o início do movimento da partícula.
Devido à ampla variedade de aplicações, o início do movimento da partícula foi estudado extensivamente ao longo de um século, principalmente sob condições turbulentas7,8,9,10,11, 12,13,14,15. Muitas abordagens experimentais foram aplicadas para determinar o limiar para o início do movimento. Os estudos incluem parâmetros tais como a partícula Reynolds número13,16,17,18,19,20, a submersão de fluxo relativo 21 , 22 , 23 , 24 ou fatores geométricos como o ângulo do repose16,18,25, exposição para o fluxo26,,27,28,29, protrusão de grão relativo29 ou cama streamwise inclinação30.
Os dados atuais para o limiar incluindo condições turbulentas estão amplamente espalhados12,31 , e os resultados muitas vezes parecem inconsistentes24. Isto é principalmente devido à complexidade inerente de controlar ou determinar parâmetros de fluxo sob condições turbulentas13,14. Além disso, o limiar para o movimento de sedimentos depende fortemente o modo de movimento, ou seja, deslizamento, rolamento ou levantamento17 e o critério para caracterizar o incipiente movimento31. Este último pode ser ambíguo em uma cama de sedimentos erodíveis.
Durante a última década, experimentais pesquisadores estudaram o movimento da partícula incipiente em fluxos laminar32,33,34,35,36,37, 38 , 39 , 40 , 41 , 42 , 43 , 44, onde o amplo espectro de escalas de comprimento interagindo com a cama é evitado45. Em muitos cenários práticos que implica sedimentação, as partículas são muito pequenas e a partícula, o número de Reynolds permanece inferior a cerca de 546. Por outro lado, os fluxos laminar são capazes de gerar padrões geométricos como ondulações e dunas como escoamentos turbulentos do42,47. Similitudes em ambos os regimes foram mostrados para refletir as analogias no subjacente física47 então uma visão importante para o transporte de partículas pode ser obtida um melhor controlado sistema experimental48.
No fluxo laminar, Charru et al notou que o rearranjo de local de um leito granular de grânulos de tamanhos uniforme, chamado cama blindagem, resultou em um aumento progressivo do limiar para o início do movimento até condições saturadas foram alcançadas 32. no entanto, a literatura, revela diferentes limiares para condições saturadas em camas de sedimentos irregularmente arranjados dependendo da montagem experimental36,44. Essa dispersão pode ser devido à dificuldade de controlar parâmetros de partículas tais como orientação, nível de saliência e compactação dos sedimentos.
O objetivo principal deste manuscrito é descrever em detalhe como caracterizar o incipiente movimento de esferas única em função das Propriedades geométricas da cama horizontal de sedimentos. Para o efeito, usamos geometrias regulares, consistindo de monocamadas de grânulos fixos regularmente organizadas de acordo com configurações triangulares ou quadráticas. Substratos regulares semelhantes ao que usamos são encontrados em aplicações tais como para o modelo-conjunto de partículas em ensaios microfluidic49, auto-montagem de microdevices em geometrias estruturado confinados50 ou intrínseco induzida por partículas transporte em microcanais51. Mais importante, usar substratos regulares permite-nos para destacar o impacto da geometria local e orientação e para evitar qualquer dubiety sobre o papel da vizinhança.
No fluxo laminar, observamos que o número de escudos a crítica aumentou 50% apenas dependendo do espaçamento entre as esferas de substrato e, portanto, sobre a exposição do talão para o fluxo de38. Da mesma forma, nós encontramos que o número de escudos crítico alterado por até um fator de dois, dependendo da orientação do substrato para a direção de fluxo38. Notamos que imóveis vizinhos afetam apenas o início da esfera móvel se estivessem mais perto do que a partícula sobre três diâmetros41. Desencadeada pelas conclusões do experimento, recentemente apresentamos um modelo analítico rigoroso que prevê o número crítico de escudos no rastejamento fluxo limite40. O modelo abrange o início do movimento de altamente expostos para contas ocultas.
A primeira parte do manuscrito lida com a descrição do procedimento experimental utilizado em estudos anteriores no cisalhamento número de Reynolds, Re *, menor que 1. O fluxo laminar é induzido com uma rotação rheometer com uma configuração paralela. Este limite de número de Reynolds baixo, a partícula não é para qualquer flutuação de velocidade20 de experiência e o sistema coincide com o chamado fluxo hidraulicamente suave onde a partícula está submersa dentro da subcamada viscosa.
Uma vez que o incipiente movimento no fluxo laminar é estabelecido, o papel da turbulência pode tornar-se mais claro. Motivado por esta ideia, nós introduzimos um novo procedimento experimental na segunda parte do protocolo. Usando um túnel de vento de baixa velocidade de Göttingen com seção de teste do jato aberto, os escudos críticos número pode ser determinado em uma ampla gama de Re * incluindo o fluxo hidraulicamente transitório e regime turbulento. Os resultados experimentais podem fornecer uma importante visão sobre como as forças e torques agem sobre uma partícula devido ao fluxo turbulento, dependendo da geometria do substrato. Além disso, estes resultados podem ser usados como referência para modelos mais sofisticados em alta Re * da mesma forma que o trabalho passado em fluxo laminar tem sido utilizado para alimentar semi modelos probabilísticos52 ou validar recentes modelos numéricos53. Apresentamos alguns exemplos representativos de aplicações em Re * variando de 40 a 150.
O critério incipiente é estabelecido como o movimento da partícula única da posição de equilíbrio inicial para a próxima. Processamento de imagem é usado para determinar o modo de início do movimento, ou seja, rolamento, deslizamento, levantamento de39,41. Para esse efeito, o ângulo de rotação das esferas móveis que foram marcados manualmente é detectado. O algoritmo rastreia a posição das marcas e compara-o com o centro da esfera. Um conjunto preliminar de experimentos foi realizado em ambos os set-ups experimentais para esclarecer que o número de escudos a crítica continua a ser independente dos efeitos de tamanho finito do set-up e submersão de fluxo relativo. Os métodos experimentais destinam-se, portanto, para excluir qualquer outro parâmetro depende do número de escudos crítico além do Re * e Propriedades geométricas da cama sedimento. O Re * é variada usando diferentes combinações de fluido-partícula. O número de escudos crítico é caracterizado em função do grau de enterro,  , definido por Martino et al 37 como
, definido por Martino et al 37 como 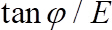 onde
onde  é o ângulo de repouso, ou seja, o ângulo crítico, no qual movimento ocorre54, e
é o ângulo de repouso, ou seja, o ângulo crítico, no qual movimento ocorre54, e  é o grau de exposição, definido como a razão entre a área transversal efetivamente exposta ao fluxo de a área transversal total da esfera móvel.
é o grau de exposição, definido como a razão entre a área transversal efetivamente exposta ao fluxo de a área transversal total da esfera móvel.
Access restricted. Please log in or start a trial to view this content.
Protocolo
1. partícula incipiente movimento no limite de fluxo rastejando.
Nota: As medições são realizadas em um rheometer rotacional que tenha sido modificado para esta aplicação específica.
- Preparando o Rheometer.
- Conecte a alimentação de ar para o rheometer para evitar danificar os rolamentos de ar. Abra a válvula além dos filtros de ar, até que seja alcançada uma pressão de aproximadamente 5 bares no sistema.
- Conecte o circulador fluido para a placa de medição. Verifique se as mangueiras do elemento Peltier são conectadas para o rheometer. Ligue o circulador fluido e regular a temperatura desejada (20 ° C).
- Monte o recipiente personalizado contendo o substrato regular sobre o rheometer.
- Leve o substrato regular fora do recipiente e limpe a superfície cuidadosamente com água destilada. Seque a superfície com uma pano de limpeza da lente e retire a poeira residual possível com um ventilador.
Nota: Os substratos regulares são monocamadas de 15 x 15 mm2 construído a partir de grânulos de vidro soda-cal esférico de µm (405.9 ± 8,7). - Usando a fita de dupla face de espessura de 0,4 mm, conserte o substrato regular para o recipiente garantindo que o centro de substrato está a uma distância de 21 mm do eixo de giro.
- Coloque o adaptador personalizado na placa do rheometer.
- Monte o recipiente circular personalizado para o prato, garantindo que a seção plana frontal está enfrentando o sistema de imagem projetado para gravação de lado.
Nota: Certifique-se que o recipiente está totalmente horizontal com o nível de água (0,6 mm/m). Para o efeito, coloque o nível de água no recipiente paralela à parte traseira do dispositivo e nivelá-lo com os pés reguláveis rheometer. Repita o procedimento para transformar o nível de água em 90 graus.
- Leve o substrato regular fora do recipiente e limpe a superfície cuidadosamente com água destilada. Seque a superfície com uma pano de limpeza da lente e retire a poeira residual possível com um ventilador.
- Ligue o rheometer. Aguarde até o procedimento de inicialização for concluído e o status de "okey" aparece na tela do dispositivo.
- Inicie o computador e o software rheometer. Inicializar o rheometer e regule a temperatura no painel de controle do software para o valor desejado (20 ° C).
- Monte o sistema de medição personalizado. Set-up a zero abertura do software.
Nota: Antes de definir o zero gap, certifique-se que não há nenhum móveis grânulos no substrato e que as fronteiras de substrato não estão dobradas. Um erro na configuração a diferença de zero vai levar a um erro sistemático no cálculo a distorcer a taxa e, portanto, na mensuração subsequente de escudos críticas número. Presume-se uma incerteza absoluta de 0,05 mm na largura da abertura ao calcular o número de escudos a crítica. - Levante a placa de medição de 30 mm e removê-lo.
- Encha o recipiente com cerca de 70 mL de óleo de silicone 100 MPa · s. Certifique-se de que o nível do líquido no recipiente permanece acima de 2 mm. O óleo de silicone não deve cobrir a parte superior da placa transparente. Espere aproximadamente 15-20 min. para o equilíbrio térmico. Durante esse tempo, ajuste os sistemas de imagem (consulte a etapa 2 do protocolo).
Nota: A temperatura que é fixada em (295.15 ± 0,5) K aqui, é controlada com um elemento Peltier conectado para o rheometer e medido com um termômetro externo. Flutuações de menos de 0,5 K são observadas durante os experimentos.
- Ajustando o sistema da imagem latente.
- Ligue a lâmpada de xenônio de arco W 300. Ajuste o guia flexível de luz para iluminar o grânulo do lado pelas paredes do recipiente transparentes.
- Ajuste a intensidade da luz LED para evitar a reflexão da luz forte sobre o substrato.
- Ajuste o sistema de imagem projetado para gravar o movimento da partícula de cima através da placa de medição transparente.
- Arranque do computador, o software de imagem e escolha o perfil monocromático na caixa de diálogo Iniciar.
- Abra a câmera CMOS de 768 x 576 do sistema de imagem instalado no topo do recipiente. Começa o vídeo ao vivo.
- Ajuste a fase de posicionamento horizontal até a posição de referência que foi anteriormente marcada no centro do substrato aparece no centro da imagem.
- Ajuste a fase de posicionamento vertical para centrar-se sobre o substrato.
- Coloca cuidadosamente uma esfera de vidro soda-cal marcado de µm (405.9 ± 8,7).
- Certifique-se de que pelo menos uma das marcas é colocada a uma distância de aproximadamente 75% do raio do grânulo ou maior do eixo de rotação. Se isso não for o caso, Mova manualmente a medição da placa para conseguir o movimento da esfera para a próxima posição de equilíbrio (ver Figura 2(a) como uma referência).
Nota: Para garantir um acompanhamento adequado durante o movimento os grânulos móveis são marcados com diversos pontos separados por cerca de 45° (veja a Figura 3(a)). O código inclui uma instrução de fluxo de controle simples para minimizar a marca misassignment para calcular o ângulo de rotação. Para obter mais detalhes, consultar Agudo et al 2017,39. - Abrir a caixa de diálogo para definir os parâmetros da câmera e ajustar a taxa de quadros 30 fps. Ajuste o tempo de exposição para garantir que as marcas são devidamente distinguidas do perímetro do grânulo.
Nota: A esfera de vidro soda-cal submergida em um óleo de silicone de 100 MPa · s requer cerca de 4 segundos para mover de sua posição inicial para o divisor de águas para a posição de equilíbrio a vizinha. Daí, um framerate de 30 fps permite uma incerteza de menos de 1%.
- Fixar a placa de medição para o rheometer.
- Defina a distância de medição a 2 mm.
Nota: O foco da câmera superior deve ser reajustado ligeiramente devido à presença da placa de Plexiglas. - Ajuste o sistema de imagem projetado para gravar o movimento da partícula do lado através do slide de microscópio transparente.
- Abra a 4912 x 3684 câmera do CMOS do sistema de imagem, instalado na frente do recipiente e iniciar o vídeo ao vivo.
- Ajuste a vertical e a fase de posicionamento horizontal colocado paralelo a rheometer até o talão marcado aparece no centro da imagem.
- Ajuste a lente de zoom modular até o campo de visão inclui a superfície superior do substrato, o talão e a parte inferior do disco medição.
- Ajuste a fase de posicionamento horizontal colocada perpendicular a rheometer para focar o talão.
- Abrir a caixa de diálogo para definir os parâmetros da câmera e ajustar a taxa de quadros 30 fps.
- Determine a velocidade de giro crítica para o início do movimento.
- Aumente linearmente a velocidade rotacional, n, de 0,02 a 0,05 revoluções por segundo em pequenos incrementos de 0,00025 revoluções por segundo utilizando o software rheometer.
- Na janela de medição, clique duas vezes na célula para o tipo de controle e edite o intervalo da velocidade de 0,02 a 0,05 revoluções por segundo.
- Clique duas vezes o tempo de configuração e digite o número de medição aponta, 60 e a duração de cada medição, 5 s.
- Defina uma tabela que representa a velocidade de rotação em função do tempo.
- Abra o vídeo ao vivo das câmeras laterais e superiores. Inicie a gravação de um vídeo-sequência de ambas as câmeras usando o software de imagem.
- Inicie a medição usando o software rheometer.
Nota: Uma experiência preliminar com um tamanho de passo maior é recomendada antes da etapa 1.3.1.1 para estimar aproximadamente o intervalo de velocidade na qual o incipiente movimento vai acontecer. A uma distância de 21 mm do eixo de giro e usando o óleo de silicone de 100 MPa · s, por exemplo, o grânulo de vidro se move ao girar a velocidades de aproximadamente 0,035 revoluções por segundo. Portanto, uma faixa de 0,02 a 0,05 revoluções por segundo parece apropriada para o experimento. - Olhe atentamente para o vídeo ao vivo do topo ou da câmera lateral e parar a medição quando o grânulo desloca-se da posição de equilíbrio. Observe a velocidade na qual o grânulo cruza o separatrix para a posição de equilíbrio a vizinha. A velocidade de rotação notável representa a velocidade de rotação crítica, n.C. Pare as sequências de vídeo.
Nota: Certifique-se que o tamanho do passo é pequeno o suficiente para que o aumento da velocidade durante o intervalo de tempo que o grânulo requer movendo-se de sua posição inicial para o vizinho que não envolve mais de 1% do valor crítico. - Coloque a pérola volta para sua posição original. Isso pode ser feito movendo manualmente o prato giratório até o talão desloca uma posição de volta. Repita a experiência cinco vezes observando a velocidade crítica média e o desvio-padrão.
- Repita as etapas 1.3.1 a 1.3.5 com um grânulo marcado diferente em 2 posições adjacentes ao centro do substrato.
- Aumente linearmente a velocidade rotacional, n, de 0,02 a 0,05 revoluções por segundo em pequenos incrementos de 0,00025 revoluções por segundo utilizando o software rheometer.
- Analisando os dados.
- Determinar o modo de movimento: analisar a sequência de imagens anteriormente gravadas de cima ou de lado com o algoritmo conforme descrito em Agudo et al . 201739.
- Determine o número de escudos a crítica e o número de Reynolds de cisalhamento.
- Obter o número de escudos a crítica da seguinte equação40
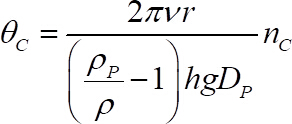 (1)
(1)
onde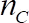 foi Obtida de passo 1.3.4,
foi Obtida de passo 1.3.4,  é a viscosidade cinemática,
é a viscosidade cinemática,  e
e  são partículas e densidades líquidas, respectivamente,
são partículas e densidades líquidas, respectivamente, 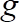 é a aceleração da gravidade e
é a aceleração da gravidade e 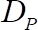 é o diâmetro do grânulo móveis, todos -los conhecido.
é o diâmetro do grânulo móveis, todos -los conhecido.  é a largura do fosso, definida como a distância da parte superior das esferas substrato para a placa de medição, ou seja, 2 mm e r é a distância radial da partícula do eixo de giro, ou seja, 21 mm.
é a largura do fosso, definida como a distância da parte superior das esferas substrato para a placa de medição, ou seja, 2 mm e r é a distância radial da partícula do eixo de giro, ou seja, 21 mm. - Obter o número de Reynolds de cisalhamento, Re * baseia-se a velocidade de cisalhamento, das seguintes equações:
 (2)
(2)
- Obter o número de escudos a crítica da seguinte equação40
- Repita o procedimento de 1.1.3 para 1.4.2 utilizando um substrato diferente de regular.
- Use o grânulo diferentes densidades e viscosidades de fluidos diferentes a fim de cobrir uma ampla gama de Re * de condições de escoamento rastejando até 1.
2. partícula incipiente movimento em Regime turbulento hidraulicamente transitório e áspero.
Nota: As medições são realizadas em um personalizado baixa velocidade-túnel de vento com seção de teste do jato aberto, tipo de Göttingen.
- Preparando o sistema da imagem latente.
- Corrigi o substrato quadrático no meio da seção de teste.
- Lugar um grânulo de alumina de 5mm previamente marcadas na posição inicial desejada (110 mm da borda esquerda e 95 mm da borda lateral).
- Conectar a câmera de alta velocidade, juntamente com a lente macro para o computador e ligá-lo. Ajuste a lente macro até o talão do alvo é claro na imagem.
- Inicie o software de imagem no computador. Ative "Câmera ao vivo" e configure-a "taxa de amostragem" a 1000 fps.
- Ligue a fonte de luz LED e ajustar a intensidade, bem como o foco da câmera para obter uma imagem clara da partícula e suas marcas.
Nota: Certifique-se que pelo menos uma das marcas é colocada a uma distância de aproximadamente 75% do raio do grânulo ou maior do eixo de rotação (ver Figura 3(a) como uma referência).
- Determinar a velocidade do ventilador crítico para o início do movimento.
- Defina a velocidade do ventilador bem abaixo do valor crítico (aproximadamente 1400 rpm para o grânulo de alumina de 5 mm).
- Inicie a gravação, pressionando o gatilho sobre o software de imagem.
- Aumentar a velocidade em passos de aproximadamente 4 a 6 rpm cada 10 s até incipiente movimento ocorre.
- Nota o valor de velocidade crítica na qual incipiente movimento ocorre e parar a sequência de vídeo.
- Coloque uma nova pérola marcada na mesma posição inicial e repita o procedimento de 2.2.1 a 2.2.4 dez vezes. Observe a velocidade crítica para cada medição.
- Repita o procedimento de 2.2.1 a 2.2.5 à mesma distância da borda esquerda, mas a 65 e 125 mm da borda lateral, respectivamente. Observe a velocidade crítica para cada medição.
- Preparando a temperatura constante ligação direta anemômetro (CTA).
- Defina a função de controle CTA a postos e a resistência de década para 00.00. Ligue a energia principal e esperar por aproximadamente 15-20 min aquecer.
- Conecte a circuito sonda e mudar a função de controle do CTA para medição de resistência. Ajuste os zero Ohms até que a agulha é colocada na marca vermelha e trocar a função de controle de volta para standby.
- Substitua a sonda circuito pela sonda miniatura Hot-Wire. Mude a função de controle do CTA para medição de resistência. Ajuste os parâmetros de resistência até que a agulha é colocada na marca vermelha.
Nota: A resistência medida corresponde a resistência fria da sonda em miniatura. O valor medido deve ser de acordo com o valor fornecido pelo fabricante (3.32 Ω). - Mude a função do CTA para preparar e ajustar a década de resistência para 5,5 Ω para atingir uma taxa de superaquecimento de cerca de 65%.
- Medir a resposta de frequência de CTA na média velocidade crítica (etapa 2.2.4).
- Ligue o ventilador e definir a velocidade de rotação do ventilador para o valor crítico, cerca de 1400 rpm. Ligue o osciloscópio.
- Ligue o gerador de onda quadrada da AIC.
- Iniciar o software de osciloscópio no computador e abra o módulo CSV para habilitar a gravação de dados. Escolha o canal (CH1) e salvar a gravação de dados ou seja, o tempo e a tensão, sob o nome de arquivo desejado. Espere até as medições acabar (cerca de 3 min).
Nota: A frequência de corte é calculada a partir do tempo de resposta na qual a tensão caiu para um nível de - 3db (consulte a Figura 4(a)). - Desligue o gerador de onda quadrada e definir a função CTA para standby.
- Calibrando o CTA.
- Interruptor da função CTA para operar. Certifique-se de que a sonda é ajustada a uma altura suficiente longe da placa para que ele está localizado na zona de fluxo livre.
- Defina a velocidade de rotação do ventilador para 200 rpm. Medir a velocidade de streamwise na zona livre fluxo usando o anemômetro do impulsor e ler a tensão no osciloscópio.
- Repita a etapa 2.4.2 para diferentes velocidades de rotação com um incremento fixo de 50 rpm até cerca de 1450 rpm (um total de 26 leituras).
- Estabelecer uma correlação entre o rpm e a velocidade de streamwise livre-fluxo medida,
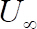 . Obter a velocidade crítica,
. Obter a velocidade crítica,  , correspondente à velocidade de rotação crítica para cada uma das medições realizadas a partir de etapas 2.2.5 para 2.2.6. Calcular a velocidade média de fluxo livre de crítica,
, correspondente à velocidade de rotação crítica para cada uma das medições realizadas a partir de etapas 2.2.5 para 2.2.6. Calcular a velocidade média de fluxo livre de crítica,  e o desvio padrão das medições.
e o desvio padrão das medições. - Estabelece uma correlação entre a velocidade e a voltagem de acordo com um ajuste polinomial de terceiro grau:
 (3)
(3)
Aqui, é a streamwise velocidade medida em m/s,
é a streamwise velocidade medida em m/s,  é a tensão medida em Volt (V), e
é a tensão medida em Volt (V), e 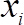 são os coeficientes de ajuste. As curvas de calibração são mostradas na Figura 4(b) antes e após as medições do perfil de velocidade.
são os coeficientes de ajuste. As curvas de calibração são mostradas na Figura 4(b) antes e após as medições do perfil de velocidade.
- Medir a velocidade de streamwise com a posição de parede-normal em condições críticas.
- Extrair o talão marcado do substrato.
- Ajuste o volante da fase de posicionamento horizontal até a sonda de fio quente é colocada na posição inicial desejada (110 mm da borda esquerda e 95 mm da borda lateral).
- Ajustar cuidadosamente o volante de vertical posicionamento estágio até a sonda é colocada como perto possível da superfície do substrato. Ver através da câmera acoplada à lente macro para garantir que o fio não toque a superfície do substrato. Defina o valor zero no indicador de nível digital naquela posição.
Atenção: O fio quente é muito sensível e se toca a superfície quebrará. Para fins de segurança, colocamos a sonda a uma distância de 0,05 mm acima do topo da esfera de substrato (ver Figura 1(e) como uma referência). Isto representa um componente de parede normal normalizado onde
onde 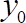 é o ponto de partida medindo valor,
é o ponto de partida medindo valor, 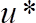 é a velocidade de cisalhamento e
é a velocidade de cisalhamento e  é a viscosidade cinemática do ar à temperatura de funcionamento. Observe que o valor inicial é abaixo
é a viscosidade cinemática do ar à temperatura de funcionamento. Observe que o valor inicial é abaixo  onde a viscosidade é dominante55.
onde a viscosidade é dominante55. - A velocidade de rotação do ventilador da velocidade rotacional média em que ocorre o movimento incipiente, consulte Etapa 2.2.4. A velocidade de fluxo livre, portanto, corresponde ao
 .
. - Ajustar a taxa de amostragem de 1 kSa e o número de amostras a 6000 no osciloscópio (total de tempo de amostragem de 6 s). Escolha o canal (CH1) e iniciar a medição. Salve os dados de gravação sob o nome de arquivo desejado. Espere até as medições acabar (cerca de 3 min).
- Aumente a posição de parede normal da sonda por um incremento de 0,01 mm até 0,4 mm e por um incremento de 0.1 mm até a altura de 10 mm. Isso corresponde a um total de 137 pontos para a curva do perfil de velocidade. Salve os dados gravados para cada altura.
- Analisando os dados.
- Calcule a velocidade média de streamwise e a intensidade turbulenta para cada posição de parede normal.
- Execute o algoritmo de auto-desenvolvimento para avaliar as quantidades de estatísticas. Abra o script e selecione a pasta que contém a curva de calibração e os dados armazenados para cada um da altura medida.
Nota: O script primeiro calcula os coeficientes de ajuste da curva de calibração, como mostrado na EQ. 3. Para cada altura, ele calcula a velocidade instantânea de streamwise,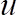 por usando a EQ. 3 e calcula a escala de tempo integral pelo método de autocorrelação56. Depois disso, ele calcula a média de tempo,
por usando a EQ. 3 e calcula a escala de tempo integral pelo método de autocorrelação56. Depois disso, ele calcula a média de tempo,  e a velocidade de raiz quadrada,
e a velocidade de raiz quadrada, 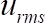 , para amostras que são separadas por duas vezes o tempo integral necessário para a análise de tempo-em média.
, para amostras que são separadas por duas vezes o tempo integral necessário para a análise de tempo-em média. - Plotar a posição vertical adimensional,
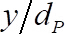 contra a velocidade média de tempo streamwise adimensional
contra a velocidade média de tempo streamwise adimensional 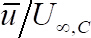 , onde
, onde 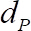 o diâmetro das esferas substrato. Lote
o diâmetro das esferas substrato. Lote 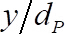 contra a velocidade quadrada raiz adimensional
contra a velocidade quadrada raiz adimensional  . Figura 4 (c)-(d) retrata os resultados para o caso do grânulo de alumina de 5 mm.
. Figura 4 (c)-(d) retrata os resultados para o caso do grânulo de alumina de 5 mm.
- Execute o algoritmo de auto-desenvolvimento para avaliar as quantidades de estatísticas. Abra o script e selecione a pasta que contém a curva de calibração e os dados armazenados para cada um da altura medida.
- Calcule a velocidade de cisalhamento a partir dos dados experimentais.
- Ajuste a velocidade média do tempo adimensional com a distribuição de velocidade logarítmica57
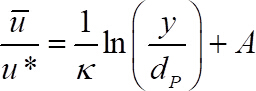 (5)
(5)
onde é a velocidade de cisalhamento,
é a velocidade de cisalhamento, 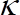 é a constante de von Karman e
é a constante de von Karman e  é uma constante que depende do número de Reynolds26de cisalhamento. A linha contínua na Figura 4(c) é um ajuste logarítmico para a velocidade média de tempo.
é uma constante que depende do número de Reynolds26de cisalhamento. A linha contínua na Figura 4(c) é um ajuste logarítmico para a velocidade média de tempo.
Nota: Desde o ajuste aos dados experimentais, pode ser mostrado que a velocidade de cisalhamento, é dada por:
é dada por: (6)
(6)
onde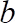 é o coeficiente de forma logarítmico e
é o coeficiente de forma logarítmico e  20.
20.
A subcamada viscosa, permanece acima da parte superior das esferas substrato em nossos experimentos. No cenário mais rigoroso, EQ. 5 deve ser substituído pela lei modificada de velocidade apresentada por Rotta20,58.
permanece acima da parte superior das esferas substrato em nossos experimentos. No cenário mais rigoroso, EQ. 5 deve ser substituído pela lei modificada de velocidade apresentada por Rotta20,58. (7)
(7)
onde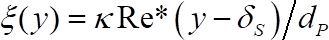 e
e 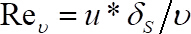 .
.  é a espessura da subcamada viscosa que pode ser aproximadamente calculada por
é a espessura da subcamada viscosa que pode ser aproximadamente calculada por  55.
55.
O algoritmo calcula diretamente a velocidade de cisalhamento do ajuste dos dados experimentais a EQ. 5 e EQ. 7. Os símbolos azuis na Figura 4(c) representam o ajuste aos dados experimentais de acordo com a EQ. 7.
No Re * acima de 70, representa até 5% do diâmetro do grânulo móvel e usando um ajuste de EQ. 5 ou 7 EQ. envolve uma variação na
representa até 5% do diâmetro do grânulo móvel e usando um ajuste de EQ. 5 ou 7 EQ. envolve uma variação na 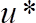 dentro da escala adotada de incerteza. Compare a linha sólida e símbolos azuis na Figura 4(c) em um Re * de cerca de 87,5.
dentro da escala adotada de incerteza. Compare a linha sólida e símbolos azuis na Figura 4(c) em um Re * de cerca de 87,5.
- Ajuste a velocidade média do tempo adimensional com a distribuição de velocidade logarítmica57
- Determinar o modo de movimento: analisar a sequência de imagens anteriormente gravadas do lado com o algoritmo, conforme descrito em Agudo et al . 201739.
- Determine o número de escudos a crítica e o número de Reynolds de cisalhamento.
- Obter o número de escudos a crítica da seguinte equação22
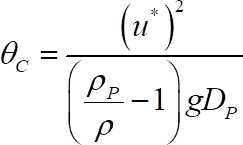 (8)
(8)
onde foi Obtida de passo 10.2,
foi Obtida de passo 10.2,  e
e  são partículas e densidade fluida, respectivamente,
são partículas e densidade fluida, respectivamente, 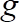 é a aceleração da gravidade e
é a aceleração da gravidade e 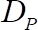 é o diâmetro do grânulo móvel, todas elas conhecidas.
é o diâmetro do grânulo móvel, todas elas conhecidas. - Obter a partícula Reynolds número, Re *, das seguintes equações:
 (9)
(9) - Repita o procedimento para medir o perfil de velocidade em função da coordenada parede normal, passo 2.5, à mesma distância da borda esquerda, mas a 65 e 125 mm na direção de largura, respectivamente.
- Repita o procedimento de 2.1 para 2.6.4.3 usando tamanhos diferentes do grânulo e substratos regulares.
- Obter o número de escudos a crítica da seguinte equação22
- Calcule a velocidade média de streamwise e a intensidade turbulenta para cada posição de parede normal.
Access restricted. Please log in or start a trial to view this content.
Resultados
Figura 1 (a) representa um esboço da montagem experimental utilizada para caracterizar o número crítico de escudos no limite de fluxo rastejando, secção 1 do protocolo. As medições são realizadas em um rheometer rotacional que foi modificado para esta aplicação específica. Uma placa de acrílico transparente de 70 mm de diâmetro foi cuidadosamente fixada a uma placa paralela de 25 mm de diâmetro. Portanto, a inércia do sistema d...
Access restricted. Please log in or start a trial to view this content.
Discussão
Apresentamos dois métodos experimentais diferentes para caracterizar o movimento de partículas incipiente como uma função da geometria da cama do sedimento. Para o efeito, usamos uma monocamada de esferas regularmente organizadas de acordo com uma simetria triangular ou quadrática, de modo que o parâmetro geométrico simplifica para uma geometria única. O limite de fluxo rastejando, descrevemos o método experimental usando um rotâmetro rotacional para induzir o fluxo de cisalhamento laminar como em anteriores es...
Access restricted. Please log in or start a trial to view this content.
Divulgações
Os autores não têm nada a divulgar
Agradecimentos
Os autores são gratos para árbitros desconhecidos para conselhos valiosos e Sukyung Choi, Byeongwoo Ko e Baekkyoung Shin para a colaboração na criação de experiências. Este trabalho foi financiado pelo projeto cérebro Busan 21 em 2017.
Access restricted. Please log in or start a trial to view this content.
Materiais
| Name | Company | Catalog Number | Comments |
| MCR 302 Rotational Rheometer | Anton Paar | Induction of shear laminar flow | |
| Measuring Plate PP25 | Anton Paar | Induction of shear laminar flow | |
| Peltier System P-PTD 200 | Anton Paar | Keep temperature of silicon oils constant in the system at laminar flow | |
| Silicone oils with viscosities of approx. 10 and 100 mPas | Basildon Chemicals | Fluid used to induced the shear in the particles | |
| Soda-lime glass beads of (405.9 ± 8.7) μm | The Technical Glass Company | Construction of the regular substrates for laminar flow conditions | |
| Opto Zoom 70 Module 0.3x-2.2x | WEISS IMAGING AND SOLUTIONS GmbH | Imaging system for recording the bead motion in the rheometer | |
| 2 x TV-Tube 1.0x, D=35 mm, L=146.5 mm | WEISS IMAGING AND SOLUTIONS GmbH | Imaging system for recording the bead motion in the rheometer | |
| UI-1220SE CMOS Camera | IDS Imaging Development Systems GmbH | Imaging system for recording the bead motion in the rheometer | |
| UI-3590CP CMOS Camera | IDS Imaging Development Systems GmbH | Imaging system for recording the bead motion in the rheometer | |
| Volpi IntraLED 3 - LED light source | Volpi USA | Imaging system for recording the bead motion in the rheometer | |
| Active light guide diameter 5mm | Volpi USA | Imaging system for recording the bead motion in the rheometer | |
| 300 Watt Xenon Arc Lamp | Newport Corporation | Imaging system for recording the bead motion in the rheometer | |
| Wind-tunnel with open jet test section, Göttingen type | Tintschl BioEnergie und Strömungstechnik AG | Induction of turbulent flow | |
| Glass spheres of (2.00 ± 0.10) mm | Gloches South Korea | Construction of the regular substrates for turbulent flow conditions | |
| Alumina spheres of (5.00 ± 0.25) mm | Gloches South Korea | Targeted bead for experiments | |
| CTA Anemometer DISA 55M01 | Disa Elektronik A/S | Measurement of flow velocity in the wind tunnel | |
| Miniaure Wire Probe Type 55P15 | Dantec Dynamics | Measurement of flow velocity in the wind tunnel | |
| HMO2022 Digital Oscilloscope, 2 Analogue. Ch., 200MHz | Rohde & Schwarz | Measurement of flow velocity in the wind tunnel | |
| Phantom Miro eX1 High-speed Camera | Vision Research IncVis | Imaging system for recording the bead motion in the wind-tunnel | |
| Canon ef 180mm f/3.5 l usm macro lens | Canon | Imaging system for recording the bead motion in the wind-tunnel | |
| Table LED Lamp | Gloches South Korea | Imaging system for recording the bead motion in the wind-tunnel |
Referências
- Groh, C., Wierschem, A., Aksel, N., Rehberg, I., Kruelle, C. A. Barchan dunes in two dimensions: Experimental tests for minimal models. Phys. Rev. E. 78, 021304(2008).
- Wierschem, A., Groh, C., Rehberg, I., Aksel, N., Kruelle, C. Ripple formation in weakly turbulent flow. Eur. Phys. J. E. 25, 213-221 (2008).
- Herrmann, H. Dune Formation in Traffic and Granular Flow. , Springer. Berlin. (2007).
- Stevanovic, V. D., et al. Analysis of transient ash pneumatic conveying over long distance and prediction of transport capacity. Powder Technol. 254, 281-290 (2014).
- Fan, F. -G., Soltani, M., Ahmadi, G., Hart, S. C. Flow-induced resuspension of rigid-link fibers from surfaces. Aerosol. Sci. Tech. 27, 97-115 (1997).
- Burdick, G., Berman, N., Beaudoin, S. Hydrodynamic particle removal from surfaces. Thin Solid Films. , 116-123 (2005).
- Chang, Y. Laboratory investigation of flume traction and transportation. Proceedings of the American Society of Civil Engineers. , 1701-1740 (1939).
- Paintal, A. A stochastic model of bed load transport. J. Hydraul. Res. 9, 527-554 (1971).
- Mantz, P. A. Incipient transport of fine grains and flakes by fluids-extended shield diagram. J. Hydr. Eng. Div.-Asce. 103, (1977).
- Yalin, M. S., Karahan, E. Inception of sediment transport. J. Hydr. Eng. Div.-Asce. 105, 1433(1979).
- Kuhnle, R. A. Incipient motion of sand-gravel sediment mixtures. J. Hydraul. Eng. 119, 1400-1415 (1993).
- Marsh, N. A., Western, A. W., Grayson, R. B. Comparison of methods for predicting incipient motion for sand beds. J. Hydraul. Eng. 130, 616-621 (2004).
- Vollmer, S., Kleinhans, M. G. Predicting incipient motion, including the effect of turbulent pressure fluctuations in the bed. Water Resour. Res. 43, (2007).
- Valyrakis, M., Diplas, P., Dancey, C. L., Greer, K., Celik, A. O. Role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res.-Earth. 115, (2010).
- Dey, S., Ali, S. Z. Stochastic mechanics of loose boundary particle transport in turbulent flow. Phys. Fluids. 29, 055103(2017).
- Wiberg, P. L., Smith, J. D. Calculations of the critical shear stress for motion of uniform and heterogeneous sediments. Water Resour. Res. 23, 1471-1480 (1987).
- Ling, C. -H. Criteria for incipient motion of spherical sediment particles. J. Hydraul. Eng. 121, 472-478 (1995).
- Dey, S. Sediment threshold. Appl. Math. Model. 23, 399-417 (1999).
- Bravo, R., Ortiz, P., Pérez-Aparicio, J. Incipient sediment transport for non-cohesive landforms by the discrete element method (DEM). Appl. Math. Model. 38, 1326-1337 (2014).
- Ali, S. Z., Dey, S. Hydrodynamics of sediment threshold. Phys. Fluids. 28, 075103(2016).
- Yalin, M. S. Mechanics of sediment transport. , Pergamon Press. California. (1977).
- Graf, W. H., Sueska, L. Sediment transport in steep channels. Journal of Hydroscience and Hydraulic Engineering. 5, 233-255 (1987).
- Recking, A. An experimental study of grain sorting effects on bedload. , Lyon. Doctor in Sciences thesis, Institut National des Sciences Appliques de Lyon (2006).
- Roušar, L., Zachoval, Z., Julien, P. Incipient motion of coarse uniform gravel. J. Hydraul. Res. 54, 615-630 (2016).
- Miller, R. L., Byrne, R. J. The angle of repose for a single grain on a fixed rough bed. Sedimentology. 6, 303-314 (1966).
- Fenton, J., Abbott, J. Initial movement of grains on a stream bed: the effect of relative protrusion. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 352, 523-537 (1977).
- Kirchner, J. W., Dietrich, W. E., Iseya, F., Ikeda, H. The variability of critical shear stress, friction angle, and grain protrusion in water-worked sediments. Sedimentology. 37, 647-672 (1990).
- Armanini, A., Gregoretti, C. Incipient sediment motion at high slopes in uniform flow condition. Water Resour. Res. 41, (2005).
- Chin, C., Chiew, Y. Effect of bed surface structure on spherical particle stability. J. Waterw. Port Coast. 119, 231-242 (1993).
- Whitehouse, R., Hardisty, J. Experimental assessment of two theories for the effect of bedslope on the threshold of bedload transport. Mar. Geol. 79, 135-139 (1988).
- Buffington, J. M., Montgomery, D. R. A systematic analysis of eight decades of incipient motion studies, with special reference to gravel-bedded rivers. Water Resour. Res. 33, 1993-2029 (1997).
- Charru, F., Mouilleron, H., Eiff, O. Erosion and deposition of particles on a bed sheared by a viscous flow. J. Fluid Mech. 519, 55-80 (2004).
- Loiseleux, T., Gondret, P., Rabaud, M., Doppler, D. Onset of erosion and avalanche for an inclined granular bed sheared by a continuous laminar flow. Phys. Fluids. 17, 103304(2005).
- Charru, F., Larrieu, E., Dupont, J. -B., Zenit, R. Motion of a particle near a rough wall in a viscous shear flow. J. Fluid Mech. 570, 431-453 (2007).
- Ouriemi, M., Aussillous, P., Medale, M., Peysson, Y., Guazzelli, É Determination of the critical Shields number for particle erosion in laminar flow. Phys. Fluids. 19, 061706(2007).
- Lobkovsky, A. E., Orpe, A. V., Molloy, R., Kudrolli, A., Rothman, D. H. Erosion of a granular bed driven by laminar fluid flow. J. Fluid Mech. 605, 47-58 (2008).
- Martino, R., Paterson, A., Piva, M. Onset of motion of a partly hidden cylinder in a laminar shear flow. Phys. Rev. E. 79, 036315(2009).
- Agudo, J., Wierschem, A. Incipient motion of a single particle on regular substrates in laminar shear flow. Phys. Fluids. 24, 093302(2012).
- Agudo, J., et al. Detection of particle motion using image processing with particular emphasis on rolling motion. Rev. Sci. Instrum. 88, 051805(2017).
- Agudo, J., et al. Shear-induced incipient motion of a single sphere on uniform substrates at low particle Reynolds numbers. J. Fluid Mech. 825, 284-314 (2017).
- Agudo, J., Dasilva, S., Wierschem, A. How do neighbors affect incipient particle motion in laminar shear flow? Phys. Fluids. 26, 053303(2014).
- Seizilles, G., Lajeunesse, E., Devauchelle, O., Bak, M. Cross-stream diffusion in bedload transport. Phys. Fluids. 26, 013302(2014).
- Seizilles, G., Devauchelle, O., Lajeunesse, E., Métivier, F. Width of laminar laboratory rivers. Phys. Rev. E. 87, 052204(2013).
- Hong, A., Tao, M., Kudrolli, A. Onset of erosion of a granular bed in a channel driven by fluid flow. Phys. Fluids. 27, 013301(2015).
- Derksen, J., Larsen, R. Drag and lift forces on random assemblies of wall-attached spheres in low-Reynolds-number shear flow. J. Fluid Mech. 673, 548-573 (2011).
- Happel, J., Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media. , Martinuis Nijhoff. The Hague. (1983).
- Lajeunesse, E., et al. Fluvial and submarine morphodynamics of laminar and near-laminar flows: A synthesis. Sedimentology. 57, 1-26 (2010).
- Aussillous, P., Chauchat, J., Pailha, M., Médale, M., Guazzelli, É Investigation of the mobile granular layer in bedload transport by laminar shearing flows. J. Fluid Mech. 736, 594-615 (2013).
- Thompson, J. A., Bau, H. H. Microfluidic, bead-based assay: Theory and experiments. J. Chromatogr. B. 878, 228-236 (2010).
- Sawetzki, T., Rahmouni, S., Bechinger, C., Marr, D. W. In situ assembly of linked geometrically coupled microdevices. Proceedings of the National Academy of Sciences. 105, 20141-20145 (2008).
- Amini, H., Sollier, E., Weaver, W. M., Di Carlo, D. Intrinsic particle-induced lateral transport in microchannels. Proceedings of the National Academy of Sciences. 109, 11593-11598 (2012).
- Soepyan, F. B., et al. Threshold velocity to initiate particle motion in horizontal and near-horizontal conduits. Powder Technol. 292, 272-289 (2016).
- Deskos, G., Diplas, P. Incipient motion of a non-cohesive particle under Stokes flow conditions. International Journal of Multiphase Flow. , (2017).
- Julien, P. Y. Erosion and sedimentation. , Cambridge University Press. Cambridge. (2010).
- Jimenez, J. Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173-196 (2004).
- O’neill, P., Nicolaides, D., Honnery, D., Soria, J. 15th Australasian Fluid Mechanics Conference. , The University of Sydney. 1-4 (2006).
- Schlichting, H. Boundary-Layer Theory. , McGraw-Hill. New York. (1979).
- Rotta, J. Das in wandnähe gültige Geschwindigkeitsgesetz turbulenter Strömungen. Arch. Appl. Mech. 18, 277-280 (1950).
- Schlichting, H., Gersten, K., Krause, E., Oertel, H. Boundary-layer theory. 7, Springer. (1955).
- Bruun, H. H. Hot-wire anemometry-principles and signal analysis. , Oxford: University Express. Oxford. (1995).
- Fan, D., Cheng, X., Wong, C. W., Li, J. -D. Optimization and Determination of the Frequency Response of Constant-Temperature Hot-Wire Anemometers. AIAA J. , 1-7 (2017).
- Valyrakis, M., Diplas, P., Dancey, C. L. Entrainment of coarse particles in turbulent flows: An energy approach. J. Geophys. Res.-Earth. 118, 42-53 (2013).
- Valyrakis, M., Diplas, P., Dancey, C. L. Entrainment of coarse grains in turbulent flows: An extreme value theory approach. Water Resour. Res. 47, (2011).
- Dey, S., Das, R., Gaudio, R., Bose, S. Turbulence in mobile-bed streams. Acta Geophys. 60, 1547-1588 (2012).
- Wu, F. -C., Chou, Y. -J. Rolling and lifting probabilities for sediment entrainment. J. Hydraul. Res. 129, 110-119 (2003).
- Leighton, D., Acrivos, A. The lift on a small sphere touching a plane in the presence of a simple shear flow. Z. Angew. Math. Phys. 36, 174-178 (1985).
- Tuyen, N. B., Cheng, N. -S. A single-camera technique for simultaneous measurement of large solid particles transported in rapid shallow channel flows. Exp. Fluids. 53, 1269-1287 (2012).
- Gollin, D., Bowman, E., Shepley, P. Methods for the physical measurement of collisional particle flows. IOP Conference Series: Earth and Environmental Science. 26, 012017(2015).
- Amon, A., et al. Focus on Imaging Methods in Granular Physics. Rev. Sci. Instrum. 88, (2017).
- Mouilleron, H., Charru, F., Eiff, O. Inside the moving layer of a sheared granular bed. J. Fluid Mech. 628, 229-239 (2009).
- Diplas, P., et al. The role of impulse on the initiation of particle movement under turbulent flow conditions. Science. 322, 717-720 (2008).
- Coleman, N. L. A theoretical and experimental study of drag and lift forces acting on a sphere resting on a hypothetical streambed. International Association for Hydraulic Research, 12th Congress, proceedings. 3, 185-192 (1967).
- El-Gabry, L. A., Thurman, D. R., Poinsatte, P. E. Procedure for determining turbulence length scales using hotwire anemometry. , NASA Technical Reports NASA/TM-2014-218403 (2014).
- Roach, P. The generation of nearly isotropic turbulence by means of grids. Int. J. Heat Fluid Fl. 8, 82-92 (1987).
Access restricted. Please log in or start a trial to view this content.
Reimpressões e Permissões
Solicitar permissão para reutilizar o texto ou figuras deste artigo JoVE
Solicitar PermissãoThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados