Se requiere una suscripción a JoVE para ver este contenido. Inicie sesión o comience su prueba gratuita.
Method Article
Visual basado en la caracterización de la propuesta del partícula incipiente en sustratos Regular: de Laminar a turbulentas condiciones
En este artículo
Resumen
Se presentan dos métodos diferentes para caracterizar el movimiento de la partícula incipiente de un solo grano en función de la geometría de la cama de sedimentos de laminar a turbulento.
Resumen
Se presentan dos métodos experimentales para determinar el umbral de movimiento de la partícula en función de las propiedades geométricas de la cama de laminar para condiciones de flujo turbulento. Para ello, el incipiente movimiento de un grano individual se estudia en sustratos regulares que constan de una monocapa de fijadas esferas de tamaño uniforme que se arreglan regularmente en simetrías triangulares y cuadráticas. El umbral se caracteriza por el número crítico de Shields. El criterio para el inicio del movimiento se define como el desplazamiento de la posición original de equilibrio a la vecina. El desplazamiento y el modo de movimiento se identifican con un sistema de proyección de imagen. El flujo laminar es inducido mediante un reómetro rotacional con una configuración de discos paralelos. La cizalla, el número de Reynolds es inferior a 1. El flujo turbulento es inducido en un túnel de viento de baja velocidad con sección de prueba de chorro abierto. La velocidad de aire se regula con un variador de frecuencia en el ventilador del soplador. El perfil de velocidad se mide con una sonda de hilo caliente conectada a un anemómetro de película caliente. El número de Reynolds del esquileo oscila entre 40 y 150. La ley logarítmica de la velocidad y la ley modificada pared presentado por Rotta se utilizan para deducir la velocidad de corte de los datos experimentales. El último es de especial interés cuando el talón móvil se expone parcialmente al flujo turbulento en el llamado régimen de flujo hidráulico transitorio. La tensión de esquileo se estima en el inicio del movimiento. Algunos resultados ilustrativos que muestran el fuerte impacto del ángulo de reposo y la exposición del grano al flujo del esquileo se representan en ambos regímenes.
Introducción
Movimiento incipiente de la partícula se encuentra en una amplia gama de procesos industriales y naturales. Ambientales por ejemplo el proceso inicial de sedimento transporte en río y los océanos, erosión de la cama o formación de dunas entre otras 1,2,3. 4de transporte neumático, eliminación de contaminantes o limpieza de superficies5,6 son aplicaciones industriales típicas que implica el inicio del movimiento de la partícula.
Debido a la amplia gama de aplicaciones, el inicio del movimiento de la partícula se ha estudiado extensivamente más de un siglo, sobre todo bajo condiciones turbulentas7,8,9,10,11, 12,13,14,15. Muchos enfoques experimentales se han aplicado para determinar el umbral para el inicio del movimiento. Los estudios incluyen parámetros como la partícula Reynolds número13,16,17,18,19,20, la sumersión de flujo relativo 21 , 22 , 23 , 24 o factores geométricos como el ángulo de reposan16,18,25, exposición al flujo26,27,28,29, relativo grano saliente29 o CBES cama cuesta30.
Los datos actuales para el umbral incluyendo condiciones turbulentas se encuentran ampliamente dispersos12,31 y los resultados a menudo parecen incompatibles24. Esto se debe principalmente a la complejidad del control o determinación de parámetros de flujo bajo condiciones turbulentas13,14. Además, el umbral para el movimiento del sedimento depende del modo de movimiento, es decir, deslizamiento, balanceo o elevación17 y el criterio para caracterizar el movimiento incipiente31. Este último puede ser ambiguo en un lecho de sedimentos erosionables.
Durante la última década, los investigadores experimentales han estudiado movimiento de partícula incipiente en flujos laminares32,33,34,35,36,37, 38 , 39 , 40 , 41 , 42 , 43 , 44, Dónde está el amplio espectro de escalas de la longitud con la cama evitar45. En muchas situaciones prácticas que implica sedimentación, las partículas son muy pequeñas y el número de Reynolds de partícula sigue siendo inferior a aproximadamente 546. Por otro lado, flujos laminares son capaces de generar patrones geométricos como ondulaciones y dunas como flujos turbulentos42,47. Similitudes en ambos regímenes se han demostrado para reflejar analogías en el subyacente física47 para que penetración importante para el transporte de la partícula puede obtenerse un mejor control de sistema experimental48.
En flujo laminar, Charru et al notar que el cambio de local de un lecho granular de granos de tamaños uniforme, cama supuesto blindaje, dio lugar a un aumento progresivo del umbral para el inicio del movimiento hasta que se lograron condiciones saturadas 32. literatura, sin embargo, revela diferentes umbrales para condiciones saturadas en lechos de sedimentos dispuestos irregularmente dependiendo el montaje experimental36,44. Esta dispersión puede deberse a la dificultad de controlar parámetros de partículas tales como orientación, nivel de la protuberancia y compactación de los sedimentos.
El objetivo principal de este manuscrito es describir en detalle cómo caracterizar el incipiente movimiento de las esferas solo en función de las propiedades geométricas de la cama de sedimentos horizontales. Para ello, utilizamos geometrías regulares, que consiste en monocapas de granos fijadas regularmente dispuestos según configuraciones triangulares o cuadráticas. Substratos regulares similar al que utilizamos se encuentran en aplicaciones tales como para el conjunto de plantilla de partículas en microfluidos ensayos49, uno mismo-Asamblea de microdispositivos en geometrías estructuradas confinados50 o intrínseca inducida por partículas transporte en microcanales51. Lo más importante, utilizando sustratos regulares permite destacar el impacto de la geometría local y orientación y para evitar cualquier inseguridad acerca del papel del barrio.
En flujo laminar, se observó que el número crítico de Shields aumentó en un 50% sólo dependiendo de la separación entre las esferas de sustrato y, por tanto, en la exposición del grano para el flujo38. Del mismo modo, encontramos que el número crítico de Shields cambiante por hasta un factor de dos dependiendo de la orientación del sustrato a la dirección de flujo38. Nos dimos cuenta que vecinos inmóviles sólo afectan el inicio de la cuenta móvil si estuvieran más cercanas que cerca de tres partícula diámetro41. Desencadenada por los resultados del experimento, recientemente hemos presentado un modelo analítico riguroso que predice el número crítico de Shields en el arrastramiento flujo límite40. El modelo cubre el inicio del movimiento de muy expuestos a perlas ocultas.
La primera parte de este manuscrito ocupa de la descripción del procedimiento experimental utilizado en estudios anteriores en el esquileo de número de Reynolds, Re *, menor que 1. El flujo laminar se induce con un reómetro rotacional con una configuración paralela. En este límite de número de Reynolds bajo, la partícula no se supone que cualquier fluctuación de velocidad20 de experiencia y el sistema coincide con el supuesto flujo hidráulicamente liso si la partícula está sumergida dentro de la subcapa viscosa.
Una vez establecido el incipiente movimiento en flujo laminar, el papel de la turbulencia puede ser más claro. Motivado por esta idea, presentamos un novedoso procedimiento experimental en la segunda parte del protocolo. Utilizando un túnel de viento de baja velocidad de Göttingen con sección de prueba de chorro abierto, los escudos críticos número puede ser determinado en una amplia gama de Re * incluyendo el flujo hidráulico transitorio y régimen turbulento. Los resultados experimentales pueden proporcionar información importante acerca de cómo las fuerzas y pares actúan en una partícula debido al flujo turbulento dependiendo de la geometría del sustrato. Además, estos resultados pueden ser utilizados como punto de referencia para los modelos más sofisticados en alta Re * de manera similar que trabajo en flujo laminar en el pasado se ha utilizado para alimentar semi modelos probabilísticos52 o validar recientes modelos numéricos53. Presentamos algunos ejemplos representativos de las aplicaciones en el Re * desde 40 hasta 150.
El incipiente criterio se establece como el movimiento de la partícula individual desde su posición de equilibrio inicial a otro. Procesamiento de imágenes se utiliza para determinar el modo de inicio del movimiento, es decir, rodar, resbalar, elevación39,41. Para ello, se detecta el ángulo de rotación de esferas móviles que fueron marcados manualmente. El algoritmo de seguimiento de la posición de las marcas y compara con el centro de la esfera. Un conjunto preliminar de experimentos se llevó a cabo en ambos montajes experimentales para aclarar que el número crítico de Shields sigue siendo independiente de los efectos de tamaño finito de la configuración y la inmersión de flujo relativa. Los métodos experimentales están diseñados así para excluir cualquier otro parámetro que depende del número de escudos crítico más allá de Re * y propiedades geométricas de la cama de sedimentos. La Re * es variada con diferentes combinaciones de partículas de fluido. El número crítico de Shields se caracteriza por ser una función del grado de entierro,  , definido por Martino et al. 37 como
, definido por Martino et al. 37 como 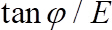 que
que  es el ángulo de reposo, es decir, el ángulo crítico en que movimiento se produce54, y
es el ángulo de reposo, es decir, el ángulo crítico en que movimiento se produce54, y  es el grado de exposición, definido como el cociente entre el área transversal efectiva expuesto al flujo al área transversal total de la cuenta móvil.
es el grado de exposición, definido como el cociente entre el área transversal efectiva expuesto al flujo al área transversal total de la cuenta móvil.
Access restricted. Please log in or start a trial to view this content.
Protocolo
1. movimiento de partículas incipiente en el límite de flujo arrastramiento.
Nota: Las mediciones se llevan a cabo en un reómetro rotacional que ha sido modificado para esta aplicación específica.
- Preparando el Reómetro.
- Conecte el suministro de aire para el Reómetro para evitar daños en los cojinetes de aire. Abra la válvula además de los filtros de aire hasta alcanza una presión de aproximadamente 5 bares en el sistema.
- Conecte la circulación fluida a la placa de medición. Asegúrese que las mangueras del elemento Peltier están conectadas al reómetro. Encienda la circulación fluida y fijar la temperatura deseada (20 ° C).
- Montar el contenedor modificado para requisitos particulares que contiene el substrato regular en el Reómetro.
- El substrato regular fuera del contenedor y limpiar la superficie cuidadosamente con agua destilada. Seque la superficie con un paño para limpiar lentes y quitar el posible polvo residual con un soplador.
Nota: Los sustratos regulares son monocapas de 15 x 15 m m2 construido a partir de granos de cristal de cal sodada esférico (405.9 ± 8.7) μm. - Usando cinta de doble cara de espesor 0,4 mm, fijar el sustrato regular en el envase asegurando que el centro del sustrato está a una distancia de 21 mm en el eje de giro.
- Coloque el adaptador personalizado en la placa del reómetro.
- Montar el contenedor circular modificada para requisitos particulares en la placa asegurando que la sección plana delantera encuentra en el sistema de imagen diseñado para grabación.
Nota: Asegúrese de que el recipiente esté completamente horizontal con el nivel de agua (0.6 mm/m). Para ello, coloque el nivel del agua en el recipiente paralelo a la parte posterior del dispositivo y nivel con las patas ajustables de reómetro. Repita el procedimiento al nivel del agua por 90 grados.
- El substrato regular fuera del contenedor y limpiar la superficie cuidadosamente con agua destilada. Seque la superficie con un paño para limpiar lentes y quitar el posible polvo residual con un soplador.
- Encienda el Reómetro. Espere hasta que termine el procedimiento de arranque y el estado "ok" aparece en la pantalla del dispositivo.
- Iniciar el ordenador y el software del reómetro. Inicializar el Reómetro y regular la temperatura desde el panel de control del software en el valor deseado (20 ° C).
- Monte el sistema de medición modificado para requisitos particulares. La brecha de cero desde el software de configuración.
Nota: Antes de ajustar el cero vacío, asegúrese de que no cuentas móviles sobre el sustrato y que las fronteras de sustrato no estén dobladas. Un error en el establecimiento de la brecha de cero conducirá a un error sistemático en el cálculo de la cizalla tasa y por lo tanto en la medición posterior de los escudos críticas número. Una incertidumbre absoluta de 0,05 mm se asume en la anchura de boquete al calcular el número crítico de Shields. - Levante la placa de medición hasta 30 m m y retírela.
- Llene el recipiente con aproximadamente 70 mL de aceite de silicona de 100 mPa·s. Asegúrese de que el nivel del líquido en el recipiente se mantiene por encima de 2 mm. Aceite de silicona no debe cubrir la parte superior de la placa transparente. Espere aproximadamente 15-20 min para el equilibrio térmico. Durante ese tiempo, ajustar los sistemas de proyección de imagen (consulte el paso 2 del Protocolo).
Nota: La temperatura que se fija (295.15 ± 0,5) K, es controlada con un elemento Peltier conectado con el Reómetro y medido con un termómetro externo. Se observan fluctuaciones de menos de 0,5 K durante los experimentos.
- Ajustar el sistema de proyección de imagen.
- Encienda la lámpara de xenón 300 W arco. Ajuste la guía de luz flexible para iluminar el grano de la parte a través de las paredes transparentes del contenedor.
- Ajustar la intensidad de luz de LED para evitar la reflexión de la luz fuerte sobre el sustrato.
- Ajustar el sistema de proyección de imagen diseñado para registrar el movimiento de la partícula de la parte superior a través de la placa de medición transparente.
- Puesta en marcha el software de proyección de imagen del ordenador y seleccione el perfil monocromo en el cuadro de diálogo de inicio.
- Abrir la cámara del CMOS 768 x 576 de lo sistema de imágenes instalado en la parte superior del contenedor. Poner en marcha el video en vivo.
- Ajuste la fase de posicionamiento horizontal hasta que aparezca la posición de referencia que ha sido previamente marcada en el centro del sustrato en el centro de la imagen.
- Ajuste la fase de posicionamiento vertical para centrarse en el sustrato.
- Coloque cuidadosamente una esfera de cristal de cal sodada marcada (405.9 ± 8.7) μm.
- Asegúrese de que al menos una de las marcas sea colocado a una distancia de aproximadamente el 75% del radio del grano más grande del eje de rotación. Si este no es el caso, mueva manualmente la medición de la placa para lograr el movimiento del grano a la siguiente posición de equilibrio (ver figura 2(a) como una referencia).
Nota: Para asegurar un seguimiento adecuado durante el movimiento las bolas móviles están marcadas con varios puntos separados por aproximadamente 45° (véase la figura 3(a)). El código incluye una instrucción de flujo de control simple para minimizar el mal asignación de marca para calcular el ángulo de rotación. Para obtener más información, nos referimos a Agudo et al. 201739. - Abra el cuadro de diálogo para configurar los parámetros de la cámara y ajustar la velocidad de fotogramas a 30 fps. Ajustar el tiempo de exposición para garantizar que las marcas se distinguen correctamente desde el perímetro del grano.
Nota: La esfera de cristal de cal sodada sumergida en un aceite de silicona de 100 mPa·s requiere 4 segundos para pasar de su posición inicial a la cuenca a la posición vecina del equilibrio. Por lo tanto, una velocidad de fotogramas de 30 fps permite una incertidumbre inferior a 1%.
- Monte la placa de medición para el Reómetro.
- Selecciona la distancia a medir 2 mm.
Nota: El foco de la cámara superior se debe reajustar ligeramente debido a la presencia de la placa de plexiglás. - Ajustar el sistema de proyección de imagen diseñado para registrar el movimiento de partículas desde el lado por el portaobjetos transparente.
- Abrir la cámara CMOS de 4912 x 3684 del sistema de imagen instalado en el frente del envase y puesta en marcha el video en vivo.
- Ajuste vertical y la etapa de posicionamiento horizontal colocado paralelo al reómetro hasta que el grano marcado aparece en el centro de la imagen.
- Ajuste el zoom modular hasta que el campo de visión incluye la superficie superior del sustrato, el talón y la parte inferior del disco de medición.
- Ajuste la fase de posicionamiento horizontal colocada perpendicular al reómetro para centrarse en el talón.
- Abra el cuadro de diálogo para configurar los parámetros de la cámara y ajustar la velocidad de fotogramas a 30 fps.
- Determinar la velocidad de rotación crítica para el inicio del movimiento.
- Aumentar linealmente la velocidad de giro, n, de 0,02 a 0,05 revoluciones por segundo en pequeños incrementos de 0,00025 revoluciones por segundo usando el software del reómetro.
- En la ventana de medición, haga doble clic en la celda para el tipo de control y modificar la gama de la velocidad de 0,02 a 0,05 revoluciones por segundo.
- Haga doble clic en el ajuste del tiempo y escriba el número de medida puntos, 60 y la duración de cada medición, 5 s.
- Establecer una tabla que representa la velocidad de rotación como función del tiempo.
- Abrir el video en vivo de las cámaras superiores y laterales. Iniciar la grabación de una secuencia de vídeo de ambas cámaras con el software de imágenes.
- Iniciar la medición con el software del reómetro.
Nota: Se recomienda un experimento preliminar con un tamaño de paso más grande antes de paso 1.3.1.1 para estimar aproximadamente la gama de la velocidad a la que va a pasar el movimiento incipiente. A una distancia de 21 mm desde el eje de giro y el aceite de silicona de 100 mPa·s, por ejemplo, el grano de cristal se mueve a velocidades de aproximadamente 0,035 revoluciones por segundo de rotación. Por lo tanto, un rango de 0,02 a 0,05 revoluciones por segundo parece apropiado para el experimento. - Mira cuidadosamente el video en vivo desde la parte superior o desde el lateral de la cámara y para la medición cuando el grano se desplaza desde su posición de equilibrio. Tenga en cuenta la velocidad a la que el grano atraviesa la línea de separación a la posición vecina del equilibrio. La velocidad de rotación indica representa la velocidad crítica de rotación, nC. Detener las secuencias de vídeo.
Nota: Asegúrese de que el tamaño de paso es lo suficientemente pequeño como para que el incremento de velocidad durante el intervalo de tiempo que el grano requiere pasar de la posición inicial a la vecina no supone más del 1% del valor crítico. - Coloque el talón en su posición original. Esto puede hacerse moviendo manualmente la placa giratoria hasta el grano desplaza una posición hacia atrás. Repetir el experimento cinco veces observando la velocidad crítica media y la desviación estándar.
- Repita los pasos 1.3.1 a 1.3.5 con un grano marcado diferentes en 2 posiciones adyacentes al centro del sustrato.
- Aumentar linealmente la velocidad de giro, n, de 0,02 a 0,05 revoluciones por segundo en pequeños incrementos de 0,00025 revoluciones por segundo usando el software del reómetro.
- Análisis de los datos.
- Determinar el modo de movimiento: analizar la secuencia de imágenes grabadas previamente desde arriba o desde el lado con el algoritmo descrito en Agudo et al 201739.
- Determinar el número crítico de Shields y la cizalla, el número de Reynolds.
- Obtener el número crítico de Shields de la siguiente ecuación40
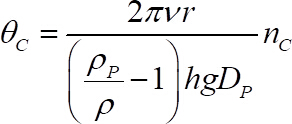 (1)
(1)
donde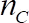 se ha obtenido de paso 1.3.4,
se ha obtenido de paso 1.3.4,  es la viscosidad cinemática,
es la viscosidad cinemática,  y
y  son partículas y densidad de líquidos, respectivamente,
son partículas y densidad de líquidos, respectivamente, 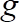 es la aceleración de la gravedad y
es la aceleración de la gravedad y 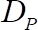 es el diámetro de grano móviles, todos de a conocer.
es el diámetro de grano móviles, todos de a conocer.  es el ancho del espacio, definido como la distancia entre la parte superior de las esferas del substrato y la placa de medición, es decir, 2 mm y r es la distancia radial de la partícula en el eje de giro, es decir, 21 mm.
es el ancho del espacio, definido como la distancia entre la parte superior de las esferas del substrato y la placa de medición, es decir, 2 mm y r es la distancia radial de la partícula en el eje de giro, es decir, 21 mm. - Obtener el corte número de Reynolds, Re * basado en la velocidad de cizalla, de las siguientes ecuaciones:
 (2)
(2)
- Obtener el número crítico de Shields de la siguiente ecuación40
- Repita el procedimiento de 1.1.3 a 1.4.2 usando un substrato regular diferentes.
- Usar grano diferentes densidades y viscosidades de fluidos diferentes para cubrir una amplia gama de Re * de arrastramiento condiciones de flujo de hasta 1.
2. movimiento de partículas incipiente en el régimen turbulento hidráulicamente rugoso y transición.
Nota: Las mediciones se llevan a cabo en un medida baja velocidad-túnel de viento con sección de prueba de chorro abierto, tipo de Göttingen.
- Preparando el sistema de proyección de imagen.
- Fijar el sustrato cuadrático en medio de la sección de prueba.
- Lugar una capa de alúmina de 5 mm previamente marcado en la posición inicial (110 mm desde el borde de ataque y 95 mm desde el borde lateral).
- Conecte la cámara de alta velocidad juntada a la lente de macro al ordenador y enciéndalo. Ajuste la lente macro hasta que el grano blanco es claro en la imagen.
- Iniciar el software de imágenes en el ordenador. Activar la "Cámara viva" y la "velocidad de muestreo" a 1000 fps.
- Encienda la fuente de luz LED y ajustar la intensidad así como el enfoque de la cámara para lograr una imagen clara de la partícula y sus marcas.
Nota: Asegúrese de que al menos una de las marcas sea colocado a una distancia de aproximadamente el 75% del radio del grano más grande del eje de rotación (ver figura 3(a) como una referencia).
- Determinar la velocidad crítica para inicio del movimiento.
- Ajustar la velocidad de ventilador muy por debajo del valor crítico (aproximadamente 1400 rpm para el grano de la alúmina de 5 mm).
- Iniciar la grabación pulsando el disparador en el software de imágenes.
- Aumentar la velocidad en pasos de aproximadamente 4 a 6 rpm cada 10 s hasta que se produzca el movimiento incipiente.
- Nota el valor de la velocidad crítica en que movimiento incipiente ocurre y detener la secuencia de vídeo.
- Coloque un nuevo grano marcado en la misma posición inicial y repetir el procedimiento desde la 2.2.1 a 2.2.4 diez veces. Tenga en cuenta la velocidad crítica para cada medición.
- Repita el procedimiento de 2.2.1 a 2.2.5 a la misma distancia desde el borde de ataque pero en 65 y 125 mm desde el borde lateral, respectivamente. Tenga en cuenta la velocidad crítica para cada medición.
- Preparación de la temperatura constante del hilo caliente anemómetro (CTA).
- Ajuste la función de control de la CTA a y la resistencia de la década a las 00.00. Encienda el interruptor principal y espere unos 15-20 min calentar.
- Conecte la punta de prueba de cortocircuito y la función de control de la CTA a la medida de la resistencia. Ajustar el cero Ohms hasta que la aguja se coloca en la marca roja y cambiar nuevamente la función de control al modo de espera.
- Vuelva a colocar la sonda cortocircuito por la sonda de alambre miniatura. Cambiar la función de control de la CTA a medida de la resistencia. Ajuste los interruptores de resistencia hasta que la aguja se coloca en la marca roja.
Nota: La resistencia corresponde a la resistencia al frío de la punta de prueba miniatura. El valor medido debe estar de acuerdo con el valor proporcionado por el fabricante (3.32 Ω). - Cambiar la función CTA y ajustar la década resistencia a 5,5 Ω para lograr una relación de sobrecalentamiento de alrededor del 65%.
- Medir la respuesta de frecuencia de la CTA a la velocidad crítica media (paso 2.2.4).
- Encienda el ventilador y ajustar la velocidad de giro del ventilador para el valor crítico, cerca de 1400 rpm. Encienda el osciloscopio.
- Encienda el generador de onda cuadrada de la CTA.
- Iniciar el software de osciloscopio en la computadora y abra el módulo CSV para permitir la grabación de datos. Seleccionar el canal (CH1) y guardar los datos de la grabación es decir tiempo y voltaje, bajo el nombre de archivo. Espere hasta que la medición final (3 min.).
Nota: La frecuencia de corte se calcula a partir del tiempo de respuesta en que la tensión se redujo a un nivel de - 3 dB (véase la figura 4(a)). - Apague el generador de onda cuadrada y ajuste la función CTA espera.
- Calibración de la CTA.
- La función CTA para operar el interruptor. Asegúrese de que la sonda se ajusta a una altura suficiente de la placa de modo que se encuentra en la zona de flujo libre.
- Ajustar la velocidad de rotación ventilador a 200 rpm. Medir la velocidad del CBES en la zona de flujo libre con el anemómetro de hélice y lea el voltaje en el osciloscopio.
- Repita el paso 2.4.2 para diferentes velocidades de rotación con un incremento fijo de 50 rpm hasta aproximadamente 1450 rpm (un total de 26 Lee).
- Establecer una correlación entre la rpm y la velocidad medida de CBES de flujo libre,
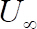 . Obtener la velocidad crítica,
. Obtener la velocidad crítica,  , correspondiente a la velocidad crítica de rotación para cada una de las mediciones realizadas de pasos 2.2.5 a 2.2.6. Calcular la velocidad media de flujo libre de crítica,
, correspondiente a la velocidad crítica de rotación para cada una de las mediciones realizadas de pasos 2.2.5 a 2.2.6. Calcular la velocidad media de flujo libre de crítica,  y la desviación estándar de las mediciones.
y la desviación estándar de las mediciones. - Establecer una correlación entre la velocidad y el voltaje según un ajuste polinomial de tercer grado:
 (3)
(3)
Aquí, se mide la velocidad del CBES en m/s,
se mide la velocidad del CBES en m/s,  es el voltaje medido en voltios (V), y
es el voltaje medido en voltios (V), y 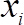 son los coeficientes de ajuste. Las curvas de calibración se muestran en la figura 4(b) antes y después de las mediciones del perfil de velocidad.
son los coeficientes de ajuste. Las curvas de calibración se muestran en la figura 4(b) antes y después de las mediciones del perfil de velocidad.
- Medición de la velocidad CBES con la posición normal de la pared en condiciones críticas.
- Quitar el grano marcado del substrato.
- Ajuste el volante de la etapa de posicionamiento horizontal hasta que la sonda de hilo caliente se coloca en la posición inicial (110 mm desde el borde de ataque y 95 mm desde el borde lateral).
- Ajustar cuidadosamente el volante de dirección de la vertical posición etapa hasta que la sonda se coloca como cerca posible de la superficie del sustrato. Ver a través de la cámara juntada a la lente macro para asegurar que el cable no toque la superficie del sustrato. Establecer el valor cero en el indicador de nivel digital en esa posición.
PRECAUCIÓN: El hilo es muy sensible y si te toca la superficie se romperá. Sea seguridad, colocamos la sonda a una distancia de 0,05 mm por encima de la parte superior de la esfera de substrato (ver figura 1(e) como una referencia). Esto representa un componente normal de pared normalizado donde
donde 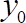 es la medición de valor, a partir
es la medición de valor, a partir 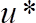 es la velocidad de corte y
es la velocidad de corte y  es la viscosidad cinemática del aire en temperatura de funcionamiento. Tenga en cuenta que el valor inicial está por debajo de
es la viscosidad cinemática del aire en temperatura de funcionamiento. Tenga en cuenta que el valor inicial está por debajo de  donde la viscosidad es dominante55.
donde la viscosidad es dominante55. - Establecer la velocidad de giro del ventilador a la velocidad de rotación media en el que ocurre el movimiento incipiente, consulte el paso 2.2.4. La velocidad de flujo libre así corresponde a
 .
. - Ajustar la frecuencia de muestreo 1 kSa y el número de muestras a 6000 en el osciloscopio (tiempo de muestreo de 6 s). Seleccionar el canal (CH1) y comenzar la medición. Guardar los datos de grabación bajo el nombre de archivo. Espere hasta que la medición final (3 min.).
- Aumentar la posición normal de la pared de la sonda por un incremento de 0.01 mm hasta 0,4 mm y por un incremento de 0,1 mm hasta la altura de 10 mm. Esto corresponde a un total de 137 puntos de la curva del perfil de velocidad. Guardar los datos registrados para cada altura.
- Análisis de los datos.
- Calcular la velocidad media de CBES y la intensidad turbulenta para cada posición de pared normal.
- Ejecutar el algoritmo desarrollado para evaluar las cantidades estadísticas. Abra la secuencia de comandos y seleccione la carpeta que contiene la curva de calibración y los datos almacenados para cada uno de la altura.
Nota: El script primero calcula los coeficientes de ajuste de la curva de calibración como se muestra en la ecuación 3. Para cada altura, calcula la velocidad instantánea del CBES,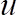 a usando la ecuación 3 y calcula la escala de tiempo integral por el método de autocorrelación56. Después de eso, calcula la media de tiempo,
a usando la ecuación 3 y calcula la escala de tiempo integral por el método de autocorrelación56. Después de eso, calcula la media de tiempo,  y la velocidad cuadrada de la raíz,
y la velocidad cuadrada de la raíz, 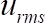 , para las muestras que están separadas por dos veces el tiempo integral necesario para el análisis de tiempo-hecha un promedio.
, para las muestras que están separadas por dos veces el tiempo integral necesario para el análisis de tiempo-hecha un promedio. - Parcela la posición vertical adimensional,
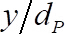 contra la velocidad promedio de tiempo adimensional de CBES
contra la velocidad promedio de tiempo adimensional de CBES 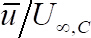 , donde
, donde 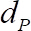 es el diámetro de las esferas de sustrato. Parcela
es el diámetro de las esferas de sustrato. Parcela 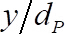 contra la velocidad cuadrada de raíz sin dimensiones
contra la velocidad cuadrada de raíz sin dimensiones  . Figura 4 (c)-(d) muestra los resultados para el caso de las bolas de alúmina 5 mm.
. Figura 4 (c)-(d) muestra los resultados para el caso de las bolas de alúmina 5 mm.
- Ejecutar el algoritmo desarrollado para evaluar las cantidades estadísticas. Abra la secuencia de comandos y seleccione la carpeta que contiene la curva de calibración y los datos almacenados para cada uno de la altura.
- Calcular la velocidad de corte de los datos experimentales.
- Ajuste la velocidad media de tiempo adimensional con la distribución de velocidad logarítmica57
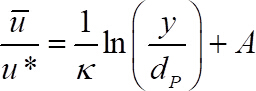 (5)
(5)
donde es la velocidad de cizalla,
es la velocidad de cizalla, 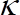 es constante del von Kármán y
es constante del von Kármán y  es una constante que depende de la cizalla Reynolds número26. La línea sólida en la figura 4(c) es un ajuste logarítmico de la velocidad media del tiempo.
es una constante que depende de la cizalla Reynolds número26. La línea sólida en la figura 4(c) es un ajuste logarítmico de la velocidad media del tiempo.
Nota: Del ajuste a los datos experimentales, puede ser demostrado que la velocidad de cizalla, está dada por:
está dada por: (6)
(6)
donde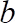 es el coeficiente de ajuste logarítmico y
es el coeficiente de ajuste logarítmico y  20.
20.
La subcapa viscosa, se mantiene por encima de la parte superior de las esferas de sustrato en nuestros experimentos. En el escenario más riguroso, ecuación 5 debería sustituirse por la ley de velocidad modificada presentada por Rotta20,58.
se mantiene por encima de la parte superior de las esferas de sustrato en nuestros experimentos. En el escenario más riguroso, ecuación 5 debería sustituirse por la ley de velocidad modificada presentada por Rotta20,58. (7)
(7)
donde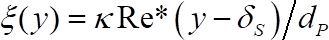 y
y 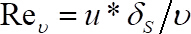 .
.  es el espesor de la subcapa viscosa que puede calcularse aproximadamente por
es el espesor de la subcapa viscosa que puede calcularse aproximadamente por  55.
55.
El algoritmo calcula directamente la velocidad de corte desde el ajuste de datos experimentales EQ. 5 y 7 EQ. Los símbolos azules en la figura 4(c) representan el ajuste a los datos experimentales según la ecuación 7.
En el Re * por encima de 70, representa hasta un 5% del diámetro de grano móvil y utilizando un ajuste de 5 EQ o EQ. 7 implica una variación en
representa hasta un 5% del diámetro de grano móvil y utilizando un ajuste de 5 EQ o EQ. 7 implica una variación en 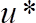 dentro de la gama aprobada de la incertidumbre. Comparar línea sólida y azul símbolos en la figura 4(c) en un Re * de aproximadamente 87.5.
dentro de la gama aprobada de la incertidumbre. Comparar línea sólida y azul símbolos en la figura 4(c) en un Re * de aproximadamente 87.5.
- Ajuste la velocidad media de tiempo adimensional con la distribución de velocidad logarítmica57
- Determinar el modo de movimiento: analizar la secuencia de imágenes grabadas previamente desde el lado con el algoritmo descrito en Agudo et al 201739.
- Determinar el número crítico de Shields y la cizalla, el número de Reynolds.
- Obtener el número crítico de Shields de la siguiente ecuación22
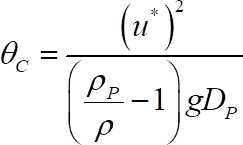 (8)
(8)
donde se ha obtenido en el paso 10.2,
se ha obtenido en el paso 10.2,  y
y  son partículas y densidad de fluido, respectivamente,
son partículas y densidad de fluido, respectivamente, 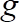 es la aceleración de la gravedad y
es la aceleración de la gravedad y 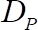 es el diámetro de grano móviles, todos ellos conocidos.
es el diámetro de grano móviles, todos ellos conocidos. - Obtener la partícula Reynolds número, Re *, de las siguientes ecuaciones:
 (9)
(9) - Repita el procedimiento para medir el perfil de velocidad en función de la coordenada de pared normal, paso 2.5, a la misma distancia desde el borde de ataque pero en 65 y 125 mm en la dirección de la anchura, respectivamente.
- Repetir el procedimiento desde 2.1 a 2.6.4.3 utilizando grano diferentes tamaños y sustratos regulares.
- Obtener el número crítico de Shields de la siguiente ecuación22
- Calcular la velocidad media de CBES y la intensidad turbulenta para cada posición de pared normal.
Access restricted. Please log in or start a trial to view this content.
Resultados
Figura 1 (a) representa un esquema del montaje experimental utilizado para caracterizar el número crítico de Shields en el límite de flujo arrastramiento, sección 1 del protocolo. Las mediciones se llevan a cabo en un reómetro rotacional que fue modificado para esta aplicación específica. Cuidadosamente se fijó una placa transparente de plexiglás de 70 mm de diámetro a una placa paralela de 25 mm de diámetro. La inercia del sistema...
Access restricted. Please log in or start a trial to view this content.
Discusión
Presentamos dos métodos experimentales para caracterizar el movimiento incipiente de la partícula en función de la geometría de la cama de sedimentos. Para ello, utilizamos una monocapa de esferas dispuestas regularmente según una simetría triangular o cuadrática de tal manera que el parámetro geométrico se simplifica a una sola geometría. En el límite de flujo arrastramiento, describimos el método experimental en un rotámetro rotacional para inducir el flujo de corte laminar como en anteriores estudios
Access restricted. Please log in or start a trial to view this content.
Divulgaciones
Los autores no tienen nada que revelar
Agradecimientos
Los autores están agradecidos a los árbitros desconocidos para valiosos consejos y Sukyung Choi, Byeongwoo Ko y Baekkyoung Shin para la colaboración en la configuración de los experimentos. Este trabajo fue apoyado por el proyecto cerebro Busan 21 en 2017.
Access restricted. Please log in or start a trial to view this content.
Materiales
| Name | Company | Catalog Number | Comments |
| MCR 302 Rotational Rheometer | Anton Paar | Induction of shear laminar flow | |
| Measuring Plate PP25 | Anton Paar | Induction of shear laminar flow | |
| Peltier System P-PTD 200 | Anton Paar | Keep temperature of silicon oils constant in the system at laminar flow | |
| Silicone oils with viscosities of approx. 10 and 100 mPas | Basildon Chemicals | Fluid used to induced the shear in the particles | |
| Soda-lime glass beads of (405.9 ± 8.7) μm | The Technical Glass Company | Construction of the regular substrates for laminar flow conditions | |
| Opto Zoom 70 Module 0.3x-2.2x | WEISS IMAGING AND SOLUTIONS GmbH | Imaging system for recording the bead motion in the rheometer | |
| 2 x TV-Tube 1.0x, D=35 mm, L=146.5 mm | WEISS IMAGING AND SOLUTIONS GmbH | Imaging system for recording the bead motion in the rheometer | |
| UI-1220SE CMOS Camera | IDS Imaging Development Systems GmbH | Imaging system for recording the bead motion in the rheometer | |
| UI-3590CP CMOS Camera | IDS Imaging Development Systems GmbH | Imaging system for recording the bead motion in the rheometer | |
| Volpi IntraLED 3 - LED light source | Volpi USA | Imaging system for recording the bead motion in the rheometer | |
| Active light guide diameter 5mm | Volpi USA | Imaging system for recording the bead motion in the rheometer | |
| 300 Watt Xenon Arc Lamp | Newport Corporation | Imaging system for recording the bead motion in the rheometer | |
| Wind-tunnel with open jet test section, Göttingen type | Tintschl BioEnergie und Strömungstechnik AG | Induction of turbulent flow | |
| Glass spheres of (2.00 ± 0.10) mm | Gloches South Korea | Construction of the regular substrates for turbulent flow conditions | |
| Alumina spheres of (5.00 ± 0.25) mm | Gloches South Korea | Targeted bead for experiments | |
| CTA Anemometer DISA 55M01 | Disa Elektronik A/S | Measurement of flow velocity in the wind tunnel | |
| Miniaure Wire Probe Type 55P15 | Dantec Dynamics | Measurement of flow velocity in the wind tunnel | |
| HMO2022 Digital Oscilloscope, 2 Analogue. Ch., 200MHz | Rohde & Schwarz | Measurement of flow velocity in the wind tunnel | |
| Phantom Miro eX1 High-speed Camera | Vision Research IncVis | Imaging system for recording the bead motion in the wind-tunnel | |
| Canon ef 180mm f/3.5 l usm macro lens | Canon | Imaging system for recording the bead motion in the wind-tunnel | |
| Table LED Lamp | Gloches South Korea | Imaging system for recording the bead motion in the wind-tunnel |
Referencias
- Groh, C., Wierschem, A., Aksel, N., Rehberg, I., Kruelle, C. A. Barchan dunes in two dimensions: Experimental tests for minimal models. Phys. Rev. E. 78, 021304(2008).
- Wierschem, A., Groh, C., Rehberg, I., Aksel, N., Kruelle, C. Ripple formation in weakly turbulent flow. Eur. Phys. J. E. 25, 213-221 (2008).
- Herrmann, H. Dune Formation in Traffic and Granular Flow. , Springer. Berlin. (2007).
- Stevanovic, V. D., et al. Analysis of transient ash pneumatic conveying over long distance and prediction of transport capacity. Powder Technol. 254, 281-290 (2014).
- Fan, F. -G., Soltani, M., Ahmadi, G., Hart, S. C. Flow-induced resuspension of rigid-link fibers from surfaces. Aerosol. Sci. Tech. 27, 97-115 (1997).
- Burdick, G., Berman, N., Beaudoin, S. Hydrodynamic particle removal from surfaces. Thin Solid Films. , 116-123 (2005).
- Chang, Y. Laboratory investigation of flume traction and transportation. Proceedings of the American Society of Civil Engineers. , 1701-1740 (1939).
- Paintal, A. A stochastic model of bed load transport. J. Hydraul. Res. 9, 527-554 (1971).
- Mantz, P. A. Incipient transport of fine grains and flakes by fluids-extended shield diagram. J. Hydr. Eng. Div.-Asce. 103, (1977).
- Yalin, M. S., Karahan, E. Inception of sediment transport. J. Hydr. Eng. Div.-Asce. 105, 1433(1979).
- Kuhnle, R. A. Incipient motion of sand-gravel sediment mixtures. J. Hydraul. Eng. 119, 1400-1415 (1993).
- Marsh, N. A., Western, A. W., Grayson, R. B. Comparison of methods for predicting incipient motion for sand beds. J. Hydraul. Eng. 130, 616-621 (2004).
- Vollmer, S., Kleinhans, M. G. Predicting incipient motion, including the effect of turbulent pressure fluctuations in the bed. Water Resour. Res. 43, (2007).
- Valyrakis, M., Diplas, P., Dancey, C. L., Greer, K., Celik, A. O. Role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res.-Earth. 115, (2010).
- Dey, S., Ali, S. Z. Stochastic mechanics of loose boundary particle transport in turbulent flow. Phys. Fluids. 29, 055103(2017).
- Wiberg, P. L., Smith, J. D. Calculations of the critical shear stress for motion of uniform and heterogeneous sediments. Water Resour. Res. 23, 1471-1480 (1987).
- Ling, C. -H. Criteria for incipient motion of spherical sediment particles. J. Hydraul. Eng. 121, 472-478 (1995).
- Dey, S. Sediment threshold. Appl. Math. Model. 23, 399-417 (1999).
- Bravo, R., Ortiz, P., Pérez-Aparicio, J. Incipient sediment transport for non-cohesive landforms by the discrete element method (DEM). Appl. Math. Model. 38, 1326-1337 (2014).
- Ali, S. Z., Dey, S. Hydrodynamics of sediment threshold. Phys. Fluids. 28, 075103(2016).
- Yalin, M. S. Mechanics of sediment transport. , Pergamon Press. California. (1977).
- Graf, W. H., Sueska, L. Sediment transport in steep channels. Journal of Hydroscience and Hydraulic Engineering. 5, 233-255 (1987).
- Recking, A. An experimental study of grain sorting effects on bedload. , Lyon. Doctor in Sciences thesis, Institut National des Sciences Appliques de Lyon (2006).
- Roušar, L., Zachoval, Z., Julien, P. Incipient motion of coarse uniform gravel. J. Hydraul. Res. 54, 615-630 (2016).
- Miller, R. L., Byrne, R. J. The angle of repose for a single grain on a fixed rough bed. Sedimentology. 6, 303-314 (1966).
- Fenton, J., Abbott, J. Initial movement of grains on a stream bed: the effect of relative protrusion. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 352, 523-537 (1977).
- Kirchner, J. W., Dietrich, W. E., Iseya, F., Ikeda, H. The variability of critical shear stress, friction angle, and grain protrusion in water-worked sediments. Sedimentology. 37, 647-672 (1990).
- Armanini, A., Gregoretti, C. Incipient sediment motion at high slopes in uniform flow condition. Water Resour. Res. 41, (2005).
- Chin, C., Chiew, Y. Effect of bed surface structure on spherical particle stability. J. Waterw. Port Coast. 119, 231-242 (1993).
- Whitehouse, R., Hardisty, J. Experimental assessment of two theories for the effect of bedslope on the threshold of bedload transport. Mar. Geol. 79, 135-139 (1988).
- Buffington, J. M., Montgomery, D. R. A systematic analysis of eight decades of incipient motion studies, with special reference to gravel-bedded rivers. Water Resour. Res. 33, 1993-2029 (1997).
- Charru, F., Mouilleron, H., Eiff, O. Erosion and deposition of particles on a bed sheared by a viscous flow. J. Fluid Mech. 519, 55-80 (2004).
- Loiseleux, T., Gondret, P., Rabaud, M., Doppler, D. Onset of erosion and avalanche for an inclined granular bed sheared by a continuous laminar flow. Phys. Fluids. 17, 103304(2005).
- Charru, F., Larrieu, E., Dupont, J. -B., Zenit, R. Motion of a particle near a rough wall in a viscous shear flow. J. Fluid Mech. 570, 431-453 (2007).
- Ouriemi, M., Aussillous, P., Medale, M., Peysson, Y., Guazzelli, É Determination of the critical Shields number for particle erosion in laminar flow. Phys. Fluids. 19, 061706(2007).
- Lobkovsky, A. E., Orpe, A. V., Molloy, R., Kudrolli, A., Rothman, D. H. Erosion of a granular bed driven by laminar fluid flow. J. Fluid Mech. 605, 47-58 (2008).
- Martino, R., Paterson, A., Piva, M. Onset of motion of a partly hidden cylinder in a laminar shear flow. Phys. Rev. E. 79, 036315(2009).
- Agudo, J., Wierschem, A. Incipient motion of a single particle on regular substrates in laminar shear flow. Phys. Fluids. 24, 093302(2012).
- Agudo, J., et al. Detection of particle motion using image processing with particular emphasis on rolling motion. Rev. Sci. Instrum. 88, 051805(2017).
- Agudo, J., et al. Shear-induced incipient motion of a single sphere on uniform substrates at low particle Reynolds numbers. J. Fluid Mech. 825, 284-314 (2017).
- Agudo, J., Dasilva, S., Wierschem, A. How do neighbors affect incipient particle motion in laminar shear flow? Phys. Fluids. 26, 053303(2014).
- Seizilles, G., Lajeunesse, E., Devauchelle, O., Bak, M. Cross-stream diffusion in bedload transport. Phys. Fluids. 26, 013302(2014).
- Seizilles, G., Devauchelle, O., Lajeunesse, E., Métivier, F. Width of laminar laboratory rivers. Phys. Rev. E. 87, 052204(2013).
- Hong, A., Tao, M., Kudrolli, A. Onset of erosion of a granular bed in a channel driven by fluid flow. Phys. Fluids. 27, 013301(2015).
- Derksen, J., Larsen, R. Drag and lift forces on random assemblies of wall-attached spheres in low-Reynolds-number shear flow. J. Fluid Mech. 673, 548-573 (2011).
- Happel, J., Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media. , Martinuis Nijhoff. The Hague. (1983).
- Lajeunesse, E., et al. Fluvial and submarine morphodynamics of laminar and near-laminar flows: A synthesis. Sedimentology. 57, 1-26 (2010).
- Aussillous, P., Chauchat, J., Pailha, M., Médale, M., Guazzelli, É Investigation of the mobile granular layer in bedload transport by laminar shearing flows. J. Fluid Mech. 736, 594-615 (2013).
- Thompson, J. A., Bau, H. H. Microfluidic, bead-based assay: Theory and experiments. J. Chromatogr. B. 878, 228-236 (2010).
- Sawetzki, T., Rahmouni, S., Bechinger, C., Marr, D. W. In situ assembly of linked geometrically coupled microdevices. Proceedings of the National Academy of Sciences. 105, 20141-20145 (2008).
- Amini, H., Sollier, E., Weaver, W. M., Di Carlo, D. Intrinsic particle-induced lateral transport in microchannels. Proceedings of the National Academy of Sciences. 109, 11593-11598 (2012).
- Soepyan, F. B., et al. Threshold velocity to initiate particle motion in horizontal and near-horizontal conduits. Powder Technol. 292, 272-289 (2016).
- Deskos, G., Diplas, P. Incipient motion of a non-cohesive particle under Stokes flow conditions. International Journal of Multiphase Flow. , (2017).
- Julien, P. Y. Erosion and sedimentation. , Cambridge University Press. Cambridge. (2010).
- Jimenez, J. Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173-196 (2004).
- O’neill, P., Nicolaides, D., Honnery, D., Soria, J. 15th Australasian Fluid Mechanics Conference. , The University of Sydney. 1-4 (2006).
- Schlichting, H. Boundary-Layer Theory. , McGraw-Hill. New York. (1979).
- Rotta, J. Das in wandnähe gültige Geschwindigkeitsgesetz turbulenter Strömungen. Arch. Appl. Mech. 18, 277-280 (1950).
- Schlichting, H., Gersten, K., Krause, E., Oertel, H. Boundary-layer theory. 7, Springer. (1955).
- Bruun, H. H. Hot-wire anemometry-principles and signal analysis. , Oxford: University Express. Oxford. (1995).
- Fan, D., Cheng, X., Wong, C. W., Li, J. -D. Optimization and Determination of the Frequency Response of Constant-Temperature Hot-Wire Anemometers. AIAA J. , 1-7 (2017).
- Valyrakis, M., Diplas, P., Dancey, C. L. Entrainment of coarse particles in turbulent flows: An energy approach. J. Geophys. Res.-Earth. 118, 42-53 (2013).
- Valyrakis, M., Diplas, P., Dancey, C. L. Entrainment of coarse grains in turbulent flows: An extreme value theory approach. Water Resour. Res. 47, (2011).
- Dey, S., Das, R., Gaudio, R., Bose, S. Turbulence in mobile-bed streams. Acta Geophys. 60, 1547-1588 (2012).
- Wu, F. -C., Chou, Y. -J. Rolling and lifting probabilities for sediment entrainment. J. Hydraul. Res. 129, 110-119 (2003).
- Leighton, D., Acrivos, A. The lift on a small sphere touching a plane in the presence of a simple shear flow. Z. Angew. Math. Phys. 36, 174-178 (1985).
- Tuyen, N. B., Cheng, N. -S. A single-camera technique for simultaneous measurement of large solid particles transported in rapid shallow channel flows. Exp. Fluids. 53, 1269-1287 (2012).
- Gollin, D., Bowman, E., Shepley, P. Methods for the physical measurement of collisional particle flows. IOP Conference Series: Earth and Environmental Science. 26, 012017(2015).
- Amon, A., et al. Focus on Imaging Methods in Granular Physics. Rev. Sci. Instrum. 88, (2017).
- Mouilleron, H., Charru, F., Eiff, O. Inside the moving layer of a sheared granular bed. J. Fluid Mech. 628, 229-239 (2009).
- Diplas, P., et al. The role of impulse on the initiation of particle movement under turbulent flow conditions. Science. 322, 717-720 (2008).
- Coleman, N. L. A theoretical and experimental study of drag and lift forces acting on a sphere resting on a hypothetical streambed. International Association for Hydraulic Research, 12th Congress, proceedings. 3, 185-192 (1967).
- El-Gabry, L. A., Thurman, D. R., Poinsatte, P. E. Procedure for determining turbulence length scales using hotwire anemometry. , NASA Technical Reports NASA/TM-2014-218403 (2014).
- Roach, P. The generation of nearly isotropic turbulence by means of grids. Int. J. Heat Fluid Fl. 8, 82-92 (1987).
Access restricted. Please log in or start a trial to view this content.
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoThis article has been published
Video Coming Soon
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados