Aby wyświetlić tę treść, wymagana jest subskrypcja JoVE. Zaloguj się lub rozpocznij bezpłatny okres próbny.
Method Article
A Computational Modeling Approach to Investigate the Influence of Hyperthermia on the Tumor Microenvironment
W tym Artykule
Podsumowanie
The article describes a protocol to simulate the transient temperature profiles and the coupled spatiotemporal variation of the interstitial fluid pressure following the heating delivered by a dipolar radiofrequency hyperthermia system. The protocol can be used to assess the response of biophysical parameters characterizing the tumor microenvironment to interventional hyperthermia techniques.
Streszczenie
The biophysical properties of the tumor microenvironment differ substantially from normal tissues. A constellation of features, including decreased vascularity, lack of lymphatic drainage, and elevated interstitial pressure, diminishes the penetration of therapeutics into tumors. Local hyperthermia within the tumor can alter microenvironmental properties, such as interstitial fluid pressure, potentially leading to improvements in drug penetration. In this context, multi-physics computational models can provide insight into the interplay between the biophysical parameters within the tumor microenvironment and can guide the design and interpretation of experiments that test the bioeffects of local hyperthermia.
This paper describes a step-by-step workflow for a computational model coupling partial differential equations describing electrical current distribution, bioheat transfer, and fluid dynamics. The main objective is to study the effects of hyperthermia delivered by a bipolar radiofrequency device on the interstitial fluid pressure within the tumor. The system of mathematical expressions linking electrical current distribution, bioheat transfer, and interstitial fluid pressure is presented, emphasizing the changes in the distribution of the interstitial fluid pressure that could be induced by the thermal intervention.
Wprowadzenie
Elevated interstitial fluid pressure (IFP) is a hallmark of solid tumors1. The leakage of fluid into the interstitium from hyperpermeable blood vessels is imbalanced by the egress of fluid due to compressed intratumoral veins and absent lymphatics1,2,3. In concert with other biophysical parameters that are abnormal within the tumor microenvironment (TME), including solid stress and stiffness, elevated IFP undermines the efficacy of both systemic and local drug delivery4,5,6. Interstitial fluid pressure in solid tumors ranges from 5 mmHg (glioblastoma and melanoma) to 30 mmHg (renal cell carcinoma) compared to 1-3 mmHg in normal tissue2. High IFP is responsible for increasing the fluid flow toward the margin of the tumor and exposes stromal cells, infiltrated cells, and other extracellular components to shear stress1,4. Mechano-biological alterations sustain an immunosuppressive TME, for example, by increasing endothelial sprouting, which supports angiogenesis, cancer cell migration and invasion, transforming growth factor-β (TGF-β) expression, and stromal stiffening7,8,9.
Several studies have explored energy-based therapies with the intent of decreasing IFP, including low-intensity ultrasound, high-intensity focused ultrasound, pulsed electric fields, and thermal therapies5,10,11. Heating to temperatures in the range of 40-43 °C, referred to as mild hyperthermia, has been shown to increase tumor blood perfusion and may thus contribute to expanding compressed veins and reducing vascular pressure by facilitating intravasation and drainage of interstitial fluid11,12. Some recent studies have shown the potential of hyperthermia to reduce IFP and consequently, to facilitate the distribution of drug or contrast agents within a tumor13,14. These studies also show increased T-cell infiltration following hyperthermia compared to no treatment control groups13.
The promising results from in vivo small animal experiments motivate further studies employing computational approaches to advance the understanding of how physical parameters within the TME are affected by physical interventions4,15,16,17. Results from computational models can complement in vivo experimental studies to uncover the cause-effect relationship underlying the local heating (or other external energy sources) and the IFP. This can be particularly instructive given the challenges with measuring spatial variations in IFP with catheter- and needle-based pressure transducers, which typically provide point measurements9,16,18,19. In the context of drug delivery, an understanding of the key biophysical mechanisms is essential to define the appropriate heating protocol as well as the time window for drug injection to enhance the likelihood of effective drug distribution. Quantitative information in terms of changes in biophysical characteristics of the TME, including but not limited to the IFP, could also give insights into the interpretation of the immunological response (e.g., T-cell infiltration) to external stimuli.
We present a protocol for computational modeling of thermally mediated changes to tumor IFP profiles. Specifically, the protocol details how to model a custom small-animal apparatus for delivering controlled thermal therapy with radiofrequency current, simulate transient temperature profiles following heating, and couple fluid dynamic simulations to compute the spatio-temporal variation of tumor IFP in response to thermal therapy. This model mirrors the essential features of the experimental setup we used in a subcutaneous tumor model (McArdle RH7777, ATCC) in a prior experimental study20.
Figure 1 shows the computational model we implemented to calculate thermally induced changes in IFP in a tumor surrounded by normal tissue. A pair of hypodermic needles inserted in the tumor is modeled to deliver heating with radiofrequency current at 500 kHz. A porous material is assumed in the tumor domain, composed of two phases: the solid phase represents the solid extracellular matrix, and the fluid phase represents the interstitial fluid. In the case of a pressure change or a matrix deformation resulting from an external stimulus, for example increase of temperature, the solid and fluid components rearrange. This causes the movement of the interstitial fluid through the extracellular solid matrix16,17,21.
From the poroelasticity theory, the stress tensor S (Pa) (equation [1]) is the combination of the elastic term describing the change in volume of the solid component relative to the initial conditions, and a porous term describing the stress induced by the hydrostatic pressure of the fluid component.
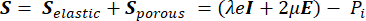 (1)
(1)
Where, λ, μ (Pa) are the Lamé parameters, E is the strain tensor, e is the volumetric strain tensor, Pi (Pa) is the interstitial fluid pressure (I is the identity matrix). Steady-state conditions are assumed for the solid component under poroelastic stress, which means that the stress tensor components are orthogonal, 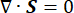 .
.
Figure 2 shows the system of mathematical equations implemented in the described poroelastic model and the interplay between the components of the presented multi-physics model. The workflow of the computational simulations includes:
Electrical problem equations. The solution of the electrical problem equations provides the time-averaged RF heat source Q (Joule heating). To this end, a quasi-static approximation to Maxwell's equations is used to calculate the distribution of the time-averaged electric field E (V/m) (Figure 2, block 1).
Thermal problem equations. The solution of the Pennes bioheat equation (Figure 2, block 2) provides the spatial and temporal variation of the temperature T (°C) as a result of the heat source (Q) linked to the absorbed electromagnetic energy, the passive heating linked to the thermal conduction of the tissues (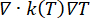 ), and the heat sink effect of the tissue blood perfusion (cWb(T) (T - Tb)). The heat sink term approximates the heat exchange between the blood flowing in the microvasculature and adjacent tissue where electromagnetic power is absorbed. The heat transfer equation also includes the advection term (
), and the heat sink effect of the tissue blood perfusion (cWb(T) (T - Tb)). The heat sink term approximates the heat exchange between the blood flowing in the microvasculature and adjacent tissue where electromagnetic power is absorbed. The heat transfer equation also includes the advection term (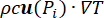 ), which describes the change in the temperature caused by the movement of interstitial fluid through the extracellular matrix of the poroelastic model. However, this term has a negligible impact on the temperature profile compared to the other mechanisms responsible for the temperature change.
), which describes the change in the temperature caused by the movement of interstitial fluid through the extracellular matrix of the poroelastic model. However, this term has a negligible impact on the temperature profile compared to the other mechanisms responsible for the temperature change.
Fluid-dynamic problem equations. The conservation of mass equation (Figure 2, block 3) combined with Darcy's law (Figure 2, block 4) gives as an output the spatial and temporal variation of the interstitial fluid pressure Pi resulting from the balance between the source (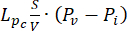 ) and the sink (
) and the sink (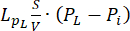 ) of the fluid. The transient pressure term on the left side of the mass conservation equation,
) of the fluid. The transient pressure term on the left side of the mass conservation equation, 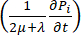 , describes the rearrangement of the fluid and solid components in the poroelastic material. This is caused by the variation of the interstitial fluid pressure, Pi, driven by the variation of the vascular pressure Pv as a function of the temperature.
, describes the rearrangement of the fluid and solid components in the poroelastic material. This is caused by the variation of the interstitial fluid pressure, Pi, driven by the variation of the vascular pressure Pv as a function of the temperature.
The difference between the vascular pressure (Pv) and the interstitial fluid pressure (Pi) is the source of the fluid that flows through the extracellular matrix. The sink term is linked to the pressure difference between the lymphatic vessels (PL) and the interstitial space (Pi). In normal tissue, the pressure in the lymphatic vasculature (~ -6-0 mmHg) is up to two-fold lower than the interstitial fluid pressure13. This pressure difference ensures the efficacy of the lymphatic vessels to drain the excess of the fluid extravasating from the wall of blood vessels into the interstitium. For the tumor model presented here, we neglected the contribution of the lymphatic system4,16,22.
Mathematical expressions from Equations (2) to (5) are used to describe the temperature dependence of the electrical and thermal conductivity of tissue and tissue blood perfusion23,24. Two different mathematical models are used to describe the temperature dependence of blood perfusion in the normal and tumor tissue domains, respectively24,25. The models show that the blood perfusion increases with the temperature up to nine times compared to the baseline in the normal tissue and only approximately two times of the baseline value in the tumor domain. For both models, the increase in the blood perfusion is limited to the temperatures within the mild hyperthermia range (below 45 °C). It is worth mentioning that the mathematical expressions, Equations (4) and (5), do not fully describe the mechanisms underlying the temperature-dependent changes in the blood perfusion in the two different types of tissue. However, they help represent the limited perfusion that typically characterizes the tumor microenvironment compared to normal tissues.
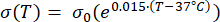 (2)
(2)
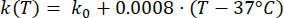 (3)
(3)
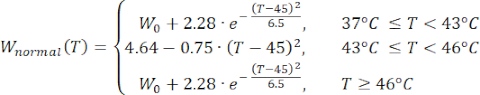 (4)
(4)
 (5)
(5)
 (6)
(6)
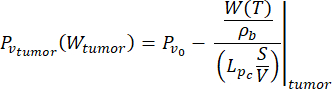 (7)
(7)
In this study, we used Equations (6) and (7) to model the vascular pressure as a function of the blood perfusion both for normal and tumor tissue models26. From Equations (4) and (5), the blood flow rate can be expressed as the ratio between the blood perfusion and the blood density. The relationship between blood flow and vascular pressure is well established in the literature3: the blood flow rate and the geometrical resistance (or conductivity, Lp) of the vasculature determine the pressure difference within the blood vessel. The vascular pressure can be expressed as a function of the temperature (Equations (6) and (7)), leveraging on this relationship and the temperature-dependent model of the blood perfusion (Equations (4) and (5)).
The implementation of the computational workflow (Figure 2) and the temperature-dependent properties of the tissue models are described in detail in the following section. All material properties and their descriptions and baseline values (i.e., at body temperature) are listed in Table 1. See the Table of Materials for details about COMSOL Multiphysics installed on a computer used to implement this computational protocol. The electrical problem was modeled using the AC/DC module; bioheat transfer was modeled using heat transfer physics; and the fluid-dynamics problem was modeled using the Mathematics interface.
Protokół
1. Build the model of a bipolar radiofrequency system
- Preliminary steps to set the interface
- Launch COMSOL Multiphysics and click on Model Wizard.
- Select 3D as Space Dimension.
- Select AC/DC Physics module | Electric Fields and Currents | Electric Currents.
- Select Heat Transfer module | Heat Transfer in Solids.
- Select Mathematics module | PDE interfaces | Coefficient Form PDE.
- Select Study | Time-dependent. Click on Done.
- Once the Comsol working space appears:
- Select Multiphysics | Electromagnetic Heating. With this step, the electromagnetic power loss density is automatically coupled as the heat source for the bioheat transfer equation.
NOTE: If Multiphysics does not appear automatically, manually specify the electromagnetic heat source (shown in COMSOL as Volumetric loss density). For more details on how to add the heat source, see 'Physics' section, step 2 'Setup for the thermal problem'. - Select Study from the top ribbon | Study Steps | Frequency Transient.
- Select Multiphysics | Electromagnetic Heating. With this step, the electromagnetic power loss density is automatically coupled as the heat source for the bioheat transfer equation.
- Define the geometries. From the top ribbon, select Geometry, then:
- Define two cones with the dimensions listed in Table 2.
- Position the cones at the distance indicated in Table 2 (spaced dinter-el apart). These two cones will model the two hypodermic needles used for building the bipolar RF system.
- Duplicate the two previous cones to model the insulation of the needles; modify the size of the cone according to the dimensions reported in Table 2.
- Select a cylinder (height, hm, and diameter dm) to model the bulk of muscle placed at z = - 9 mm (x = 0, y = 0). The values of each dimension are listed in Table 2.
- Select a cylinder (height, hs, and diameter ds) to model the thin layer of skin placed at z = 4 mm (x = 0, y = 0). The values of each dimension are listed in Table 2.
- Select a sphere (diameter, dt) to model the subcutaneous tumor placed at z = -0.5 mm (x = 0, y = 0). The size of the tumor is listed in Table 2.
- To facilitate the selection of the geometries in the following steps of the protocol, we recommend the following:
- From the Geometry ribbon, select Virtual operations | Form Composite Domains.
- Select all domains related to the electrically conductive part of the needles to create a composite geometry.
- Repeat the same procedure to create composite domains for the needle insulation geometries.
- Define the properties of the biological tissue models.
NOTE: The following steps describe the procedure to implement the mathematical expressions described by Equations (2)-(7).- From Component node, right-click to select Definitions.
- Under Functions, select Analytic.
- Specify the name of the Function (e.g., k_muscle or sigma_muscle) and type the mathematical expression consistent with Eq. 2).
- Specify temperature (T) as argument.
- Specify the Units of the function: S/m in the case of electrical conductivity.
- Repeat the previous steps from 1 to 3 to implement Eq. 3, modifying the unit accordingly (i.e., W/(m·K) for thermal conductivity).
- Specify the unit for the argument: K (kelvin) for the temperature. In Plot Parameters, specify the range of values of the function argument (i.e., temperature). To follow this protocol, use a range of 33-100 °C (306.15-373.15 K).
- Repeat the previous steps from 1 to 5 to add the temperature-dependent functions of electrical (Eq. 2) and thermal conductivities (Eq. 3) for each tissue model (i.e., muscle, skin, and tumor) using the nominal values listed in Table 1 (normal tissue refers to both muscle and skin).
- Under Functions, select Piecewise to implement Equations (4)-(7):
- Specify the name of the function.
- Specify temperature (T) as the argument of the function.
- Type the mathematical expression for each temperature interval consistent with Equations (4)-(7).
- Repeat the previous steps from 1 to 3 to add the temperature-dependent functions of blood perfusion and vascular pressure for each tissue model using the nominal values listed in Table 1 (normal tissue refers to both muscle and skin).
- Assign material properties to the geometry components.
- From the component node, select Materials.
- Select blank materials to include normal tissue, tumor tissue, blood, PTFE, and stainless steel.
- Enable manual selection and select the geometric entity corresponding to the specified material.
- Normal tissue is associated with geometries modeling muscle and skin.
- Tumor and blood tissues are associated with the tumor geometry.
- PTFE material is associated with the geometries modeling the needle insulator.
- Stainless steel material is associated with the cone geometries modeling the ground and the active needles.
- For the temperature-dependent electrical and thermal conductivities23, type the chosen name of the function and the related argument (i.e., T) that appears in the Definitions node.
- For the material properties not depending on temperature, refer to the baseline values27 listed in Table 1.
NOTE: We rely on the poroelastic theory to calculate the pressure16,17,26. The following steps show how the properties of a porous material can be assigned to a specific domain. - From Materials, select More Materials | Porous Material.
- Right-click on Porous Material to select Fluid and Solid components. Select Fluid node and under Fluid properties, select Blood (defined in the previous steps). Select Solid node and under Solid properties, select Tumor (defined in the previous steps). In the Solid node, specify the volume fraction defined as θS (Table 1).
- Enable manual selection and select the geometric entity corresponding to the specified material. To follow this protocol, assume that only the tumor region is a poroelastic domain.
- Meshing
- Under Mesh node, select Size and select a predefined Finer mesh.
- Add Free Tetrahedral feature under Mesh node. This step allows for a refined mesh in the critical areas.
NOTE: For this model, we identified the edges of the tumor and the distal end of the hypodermic needle models as critical areas. - Select the geometries of interest and customize the maximum (0.25 mm) and minimum element size in a way that the smallest component (e.g., the tip of the needle) is discretized by at least four meshing elements (complete mesh consists of 1,487,828 elements).
2. Physics
- Setup for the electrical problem
NOTE: The following steps provide information on how to set the parameters to calculate the electric field distribution (Figure 2, block 1) that will provide the radiofrequency heat source (Q).- Right-click on the Electric Currents node.
- For the electrical boundary conditions shown in Figure 3A, select Terminal and Ground as boundaries.
- For Terminal, manually select the proximal end (on the top) of one of the two needles. The identified needle will provide the input power.
- Under Terminal, select Power and specify the value according to the desired energy protocol. To follow this protocol, select 0.5 W for mild hyperthermia based on preliminary ex vivo experiments20.
- Select Ground and manually select the proximal surface of the second needle. This needle will act as a return electrode for the returning path of the electrical current.
- Apply electrical insulation to the remaining external surface of the model.
- Setup for the thermal problem
NOTE: The following steps show how to include the temperature-dependent blood perfusion functions (Equations 4 and 5) in the bioheat transfer equation to model the heat sink caused by the blood flow.- Select Heat Transfer in Solids node and specify 33 °C as the initial value of the temperature.
- To model the heat-sink effect due to the blood flow, right-click on Heat Transfer in Solids, add the Heat source domain, and select the geometry where the heat sink effect should be considered (i.e., tumor and normal tissue). Select General Source | User defined where the expression for the heat sink can be typed.
- For the thermal boundary conditions shown in Figure 3B, right-click on Heat Transfer, add Heat Flux as a boundary condition, and specify the external surfaces to which the heat flux is applied. Select Convective heat flux as the flux type. For the heat transfer coefficient, use h = 15 W/(m2 ·K) to model the mechanism of natural heat exchange between the skin and the air28. Specify the external temperature. Use T = 20 °C to model the ambient temperature in the laboratory environment.
- Setup for the fluid-dynamics problem
NOTE: The following steps describe how to implement the conservation of mass equation illustrated in Figure 2 (Block 3) and how it can be linked to the variation of the temperature.- Select Coefficient Form PDE node and specify Pressure as the dependent variable. At this stage, the unit Pascal (Pa) is automatically assigned.
NOTE: Once the simulation is computed, the results can be displayed and/or exported using the unit of choice. We present the results using mmHg unit for consistency with the literature (see the representative results section). - Specify Fluid conductance unit 1/s as source term quantity.
- Define the name to identify the variable (Pi, interstitial fluid pressure in this study).
- Right-click on Coefficient Form PDE node and select the Coefficient Form domain. Specify the geometrical entity to which the equation refers (tumor). Repeat the same steps and select the remaining tissue (normal tissue) to which a different PDE will be applied.
- For the tumor model, specify the following coefficients and terms to obtain the conservation of mass equation (Figure 2 block 3): diffusion coefficient Ki of the tumor (Table 1); damping coefficient
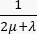 ); source term
); source term 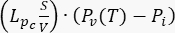 . For the tumor model, neglect the contribution of the lymphatic system. Set all other coefficients equal to zero.
. For the tumor model, neglect the contribution of the lymphatic system. Set all other coefficients equal to zero. - For the normal tissue model, specify the following coefficients and terms to obtain the conservation of mass equation (Figure 2 block 3): diffusion coefficient Ki of the normal tissue (Table 1); damping coefficient
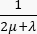 ; source term
; source term 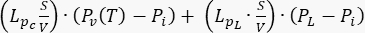 . To consider normal tissue as a normal functioning tissue, consider the contribution of the lymphatic system. Set all other coefficients equal to zero.
. To consider normal tissue as a normal functioning tissue, consider the contribution of the lymphatic system. Set all other coefficients equal to zero. - To create the link with the electromagnetic-thermal simulation, express the vascular pressure Pv as a function of the temperature (by means of the blood perfusion variable, see Equations 6 and 7).
- Right-click on Coefficient Form PDE and select Initial Values. Select the geometrical domain (tumor) and repeat the same step for the normal tissue model (normal tissue). Specify Pi0 for tumor and normal tissue according to the values listed in Table 1.
- For the boundary conditions related to the fluid-dynamic study, shown in Figure 3C, right-click on Coefficient Form PDE and select Dirichlet Boundary conditions. Select the external surface of the normal tissue domain and assign the Pi0 value corresponding to the normal tissue (Table 1).
- Select Coefficient Form PDE node and specify Pressure as the dependent variable. At this stage, the unit Pascal (Pa) is automatically assigned.
3. Run the simulations and display the results
NOTE: As a final step before computing, specify the time (simulating the duration of the procedure) and the operating frequency:
- Select Frequency-Transient from the Study node.
- Specify the time unit (s).
- From Output Times, select range (on the right side) and specify 0 s as start, 5 s as step, and 900 s as stop.
- Set the Frequency as 500e3 Hz.
- Select Compute to run the simulations.
- For the visualization of the results, select Datasets under node Results.
- Right-click to select a cut plane to define the plane to use to visualize 2D distributions (e.g., zx-plane at y = 0).
- Right-click to select a cut point in the 3D volume to display the variation of a parameter across time.
- From Results on the top ribbon,
- Select 2D plot group to visualize the two-dimensional distribution of a variable (e.g., temperature) on one of the planes identified in the steps above.
- Select 1D plot group to visualize 1D results (e.g., pressure across the time) at the point or multiple points identified in the steps above.
NOTE: The time to run the simulations with the settings described in this protocol is approximately 2.5 h.
Wyniki
The homogeneous distribution of high interstitial fluid pressure within the tumor and a drop to the normal values (0-3 mmHg) at the periphery are hallmarks of the TME. Figure 4 and Figure 5 show the initial conditions (t = 0 min) of temperature (A), interstitial fluid pressure (B), and fluid velocity (C). Before starting the heating, when the initial temperature is 33 °C, the value of interstitial fluid pressure within the tumor is approximately 9 mmHg...
Dyskusje
We present a computational modeling protocol to couple transient electric-thermal simulations with fluid-dynamic simulations to study the impact of RF-hyperthermia on thermal and interstitial fluid pressure profiles in tumors. The key aspect is in the building of a numerical workflow capable of capturing the relationship existing between temperature and vascular pressure, which in turn drives the changes in interstitial fluid pressure.
We used the relationship between vascular pressure and blo...
Ujawnienia
The authors have no conflicts of interest to disclose.
Podziękowania
The study was supported by grants from the National Science Foundation (no. 2039014) and the National Cancer Institute (R37CA269622).
Materiały
| Name | Company | Catalog Number | Comments |
| COMSOL Multiphysics (v. 6.0) | COMSOL AB, Stockholm, Sweden | Software used to implement the computational workflow described in the protocol | |
| Dell 1.8.0, 11th Gen Intel(R) Core(TM) i7-11850H @ 2.50GHz, 2496 Mhz, 8 Core(s), 16 Logical Processor(s), 32 GB RAM | Dell Inc. | Laptop used to run computational simulations |
Odniesienia
- Nia, H. T., Munn, L. L., Jain, R. K. Physical traits of cancer. Science. 370 (6516), 546-556 (2020).
- Heldin, C. -. H., Rubin, K., Pietras, K., Östman, A. High interstitial fluid pressure - an obstacle in cancer therapy. Nature Reviews Cancer. 4 (10), 806-813 (2004).
- Jain, R. K. Determinants of tumor blood flow: a review. Cancer Research. 48, 2641-2658 (1988).
- Stylianopoulos, T., Munn, L. L., Jain, R. K. Reengineering the physical microenvironment of tumors to improve drug delivery and efficacy: from mathematical modeling to bench to bedside. Trends in Cancer. 4 (4), 292-319 (2018).
- Sheth, R. A., Hesketh, R., Kong, D. S., Wicky, S., Oklu, R. Barriers to drug delivery in interventional oncology. Journal of Vascular and Interventional Radiology. 24 (8), 1201-1207 (2013).
- Chauhan, V. P., Stylianopoulos, T., Boucher, Y., Jain, R. K. Delivery of molecular and nanoscale medicine to tumors: transport barriers and strategies. Annual Review of Chemical and Biomolecular Engineering. 2 (1), 281-298 (2011).
- Li, R., et al. Interstitial flow promotes macrophage polarization toward an M2 phenotype. Molecular Biology of the Cell. 29 (16), 1927-1940 (2018).
- Stine, C. A., Munson, J. M. Autologous gradient formation under differential interstitial fluid flow environments. Biophysica. 2 (1), 16-33 (2022).
- Provenzano, P. P., et al. Enzymatic targeting of the stroma ablates physical barriers to treatment of pancreatic ductal adenocarcinoma. Cancer Cell. 21 (3), 418-429 (2012).
- Pal, K., Sheth, R. A. Engineering the tumor immune microenvironment through minimally invasive interventions. Cancers. 15 (1), 196 (2022).
- Dunne, M., Regenold, M., Allen, C. Hyperthermia can alter tumor physiology and improve chemo- and radio-therapy efficacy. Advanced Drug Delivery Reviews. 163-164, 98-124 (2020).
- Vaupel, P., et al. From localized mild hyperthermia to improved tumor oxygenation: physiological mechanisms critically involved in oncologic thermo-radio-immunotherapy. Cancers. 15 (5), 1394 (2023).
- Stapleton, S., et al. Radiation and heat improve the delivery and efficacy of nanotherapeutics by modulating intratumoral fluid dynamics. ACS Nano. 12 (8), 7583-7600 (2018).
- Li, Q., Zhou, Y., Zhang, F., McGregor, H., Yang, X. Radiofrequency hyperthermia enhances locally delivered oncolytic immuno-virotherapy for pancreatic adenocarcinoma. CardioVascular and Interventional Radiology. 45 (12), 1812-1821 (2022).
- Mpekris, F., et al. Combining microenvironment normalization strategies to improve cancer immunotherapy. Proceedings of the National Academy of Sciences. 117 (7), 3728-3737 (2020).
- Netti, P. A., Baxter, L. T., Boucher, Y., Skalak, R., Jam, R. K. Time-dependent behavior of interstitial fluid pressure in solid tumors: implications for drug delivery. Cancer Research. 15 (55), 5451-5458 (1995).
- Andreozzi, A., Iasiello, M., Netti, P. A. Effects of pulsating heat source on interstitial fluid transport in tumour tissues. Journal of The Royal Society Interface. 17 (170), 612-626 (2020).
- Leunig, M., Goetz, A. E., Messmer, K. Interstitial fluid pressure in solid tumors following hyperthermia: possible correlation with therapeutic response. Cancer Research. 52, 487-490 (1992).
- Muñoz, N. M., et al. Immune modulation by molecularly targeted photothermal ablation in a mouse model of advanced hepatocellular carcinoma and cirrhosis. Scientific Reports. 12 (1), 14449 (2022).
- Bottiglieri, A., et al. RF-hyperthermia to modulate tumor interstitial fluid pressure: an in vivo pilot study. 38th Annual Society for Thermal Medicine Meeting. , (2023).
- Baxter, L. T., Jain, R. K. Transport of fluid and macromolecules in tumors. I. Role of interstitial pressure and convection. Microvascular Research. 37 (1), 77-104 (1989).
- Stapleton, S., et al. A mathematical model of the enhanced permeability and retention effect for liposome transport in solid tumors. PLoS ONE. 8 (12), 1-10 (2013).
- Rossmann, C., Haemmerich, D. Review of temperature dependence of thermal properties, dielectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures. Critical Reviews in Biomedical Engineering. 42 (6), 467-492 (2014).
- Song, C. W., Lokshina, A., Rhee, J. G., Patten, M., Levitt, S. H. Implication of blood flow in hyperthermic treatment of tumors. IEEE Transactions on Biomedical Engineering. 31 (1), 9-16 (1984).
- Tompkins, D. T., et al. Temperature-dependent versus constant-rate blood perfusion modelling in ferromagnetic thermoseed hyperthermia: results with a model of the human prostate. International Journal of Hyperthermia. 10 (4), 517-536 (1994).
- Andreozzi, A., Iasiello, M., Netti, P. A. A thermoporoelastic model for fluid transport in tumour tissues. Journal of The Royal Society Interface. 16 (154), 0030-0046 (2019).
- Hasgall, P. A., et al. . IT'IS Database for thermal and electromagnetic parameters of biological tissues. , (2022).
- Cavagnaro, M., et al. Influence of the target tissue size on the shape of ex vivo microwave ablation zones. International Journal of Hyperthermia. 31 (1), 48-57 (2015).
- Munson, J., Shieh, A. Interstitial fluid flow in cancer: implications for disease progression and treatment. Cancer Management and Research. 19 (6), 317-328 (2014).
- Muñoz, N. M., et al. Influence of injection technique, drug formulation and tumor microenvironment on intratumoral immunotherapy delivery and efficacy. Journal for ImmunoTherapy of Cancer. 9 (2), 0018-0027 (2021).
- Swartz, M. A., Lund, A. W. Lymphatic and interstitial flow in the tumour microenvironment: linking mechanobiology with immunity. Nature Reviews Cancer. 12 (3), 210-219 (2012).
- Mehta, A., Oklu, R., Sheth, R. A. Thermal ablative therapies and immune checkpoint modulation: can locoregional approaches effect a systemic response. Gastroenterology Research and Practice. 2016, 1-11 (2016).
- Song, C. W., Park, H., Griffin, R. J. Improvement of tumor oxygenation by mild hyperthermia. Radiation Research. 155 (4), 515-528 (2001).
- Dewhirst, M. W., Oleson, J. R., Kirkpatrick, J., Secomb, T. W. Accurate three-dimensional thermal dosimetry and assessment of physiologic response are essential for optimizing thermoradiotherapy. Cancers. 14 (7), 1701 (2022).
Przedruki i uprawnienia
Zapytaj o uprawnienia na użycie tekstu lub obrazów z tego artykułu JoVE
Zapytaj o uprawnieniaPrzeglądaj więcej artyków
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Wszelkie prawa zastrzeżone