Un abonnement à JoVE est nécessaire pour voir ce contenu. Connectez-vous ou commencez votre essai gratuit.
Method Article
Une approche de modélisation computationnelle pour étudier l’influence de l’hyperthermie sur le microenvironnement tumoral
Dans cet article
Résumé
L’article décrit un protocole permettant de simuler les profils de température transitoires et la variation spatio-temporelle couplée de la pression du fluide interstitiel suite à l’échauffement délivré par un système d’hyperthermie radiofréquence dipolaire. Le protocole peut être utilisé pour évaluer la réponse des paramètres biophysiques caractérisant le microenvironnement tumoral aux techniques d’hyperthermie interventionnelle.
Résumé
Les propriétés biophysiques du microenvironnement tumoral diffèrent considérablement de celles des tissus normaux. Une constellation de caractéristiques, notamment une diminution de la vascularisation, un manque de drainage lymphatique et une pression interstitielle élevée, diminue la pénétration des traitements dans les tumeurs. L’hyperthermie locale au sein de la tumeur peut modifier les propriétés microenvironnementales, telles que la pression du liquide interstitiel, ce qui peut entraîner une amélioration de la pénétration des médicaments. Dans ce contexte, les modèles computationnels multiphysiques peuvent donner un aperçu de l’interaction entre les paramètres biophysiques au sein du microenvironnement tumoral et peuvent guider la conception et l’interprétation d’expériences qui testent les effets biologiques de l’hyperthermie locale.
Cet article décrit un flux de travail étape par étape pour un modèle informatique couplant des équations aux dérivées partielles décrivant la distribution du courant électrique, le transfert de biochaleur et la dynamique des fluides. L’objectif principal est d’étudier les effets de l’hyperthermie délivrée par un appareil de radiofréquence bipolaire sur la pression du liquide interstitiel à l’intérieur de la tumeur. Le système d’expressions mathématiques reliant la distribution du courant électrique, le transfert de biochaleur et la pression du fluide interstitiel est présenté, en mettant l’accent sur les changements dans la distribution de la pression du fluide interstitiel qui pourraient être induits par l’intervention thermique.
Introduction
Une pression liquidienne interstitielle élevée (IFP) est une caractéristique des tumeurs solides1. La fuite de liquide dans l’interstitium à partir de vaisseaux sanguins hyperperméables est déséquilibrée par l’évacuation de liquide due à des veines intratumorales comprimées et à l’absence de lymphatiques 1,2,3. De concert avec d’autres paramètres biophysiques anormaux dans le microenvironnement tumoral (TME), y compris le stress solide et la rigidité, un IFP élevé compromet l’efficacité de l’administration systémique et locale de médicaments 4,5,6. La pression du liquide interstitiel dans les tumeurs solides varie de 5 mmHg (glioblastome et mélanome) à 30 mmHg (carcinome à cellules rénales) contre 1-3 mmHg dans les tissus normaux2. Un IFP élevé est responsable de l’augmentation du flux de fluide vers la marge de la tumeur et expose les cellules stromales, les cellules infiltrées et d’autres composants extracellulaires au stress de cisaillement 1,4. Les altérations mécano-biologiques soutiennent un EUT immunosuppresseur, par exemple, en augmentant la germination endothéliale, ce qui favorise l’angiogenèse, la migration et l’invasion des cellules cancéreuses, l’expression du facteur de croissance transformant β (TGF-β) et le raidissement stromal 7,8,9.
Plusieurs études ont exploré les thérapies basées sur l’énergie dans le but de diminuer l’IFP, notamment les ultrasons de faible intensité, les ultrasons focalisés de haute intensité, les champs électriques pulsés et les thérapies thermiques 5,10,11. Il a été démontré que le chauffage à des températures comprises entre 40 et 43 °C, appelé hyperthermie légère, augmente la perfusion sanguine tumorale et peut donc contribuer à l’expansion des veines comprimées et à la réduction de la pression vasculaire en facilitant l’intravasation et le drainage du liquide interstitiel11,12. Certaines études récentes ont montré le potentiel de l’hyperthermie pour réduire l’IFP et, par conséquent, pour faciliter la distribution de médicaments ou d’agents de contraste au sein d’une tumeur13,14. Ces études montrent également une augmentation de l’infiltration des lymphocytes T après une hyperthermie par rapport aux groupes témoins sans traitement13.
Les résultats prometteurs des expériences in vivo sur de petits animaux motivent d’autres études utilisant des approches informatiques pour faire progresser la compréhension de la façon dont les paramètres physiques au sein de l’EUT sont affectés par les interventions physiques 4,15,16,17. Les résultats des modèles informatiques peuvent compléter les études expérimentales in vivo pour découvrir la relation de cause à effet sous-jacente au chauffage local (ou à d’autres sources d’énergie externes) et à l’IFP. Cela peut être particulièrement instructif compte tenu des défis liés à la mesure des variations spatiales de l’IFP avec des transducteurs de pression à cathéter et à aiguille, qui fournissent généralement des mesures ponctuelles 9,16,18,19. Dans le contexte de l’administration de médicaments, la compréhension des principaux mécanismes biophysiques est essentielle pour définir le protocole de chauffage approprié ainsi que la fenêtre temporelle pour l’injection de médicaments afin d’augmenter la probabilité d’une distribution efficace de médicaments. Des informations quantitatives sur les changements dans les caractéristiques biophysiques du TME, y compris, mais sans s’y limiter, l’IFP, pourraient également donner un aperçu de l’interprétation de la réponse immunologique (p. ex., l’infiltration des lymphocytes T) aux stimuli externes.
Nous présentons un protocole de modélisation computationnelle des modifications thermiques des profils IFP tumoraux. Plus précisément, le protocole détaille comment modéliser un appareil personnalisé pour de petits animaux pour administrer une thérapie thermique contrôlée avec un courant de radiofréquence, simuler des profils de température transitoires après chauffage et coupler des simulations de dynamique des fluides pour calculer la variation spatio-temporelle de l’IFP tumorale en réponse à la thérapie thermique. Ce modèle reflète les caractéristiques essentielles du dispositif expérimental que nous avons utilisé dans un modèle de tumeur sous-cutanée (McArdle RH7777, ATCC) dans une étude expérimentale antérieure20.
La figure 1 montre le modèle informatique que nous avons mis en œuvre pour calculer les changements thermiquement induits par l’IFP dans une tumeur entourée de tissus normaux. Une paire d’aiguilles hypodermiques insérées dans la tumeur est modélisée pour délivrer un chauffage avec un courant de radiofréquence à 500 kHz. On suppose un matériau poreux dans le domaine tumoral, composé de deux phases : la phase solide représente la matrice extracellulaire solide, et la phase fluide représente le liquide interstitiel. Dans le cas d’un changement de pression ou d’une déformation matricielle résultant d’un stimulus externe, par exemple une augmentation de la température, les composants solides et fluides se réorganisent. Cela provoque le mouvement du liquide interstitiel à travers la matrice solide extracellulaire 16,17,21.
D’après la théorie de la poroélasticité, le tenseur de contrainte S (Pa) (équation [1]) est la combinaison du terme élastique décrivant la variation de volume du composant solide par rapport aux conditions initiales, et d’un terme poreux décrivant la contrainte induite par la pression hydrostatique du composant fluide.
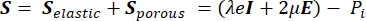 (1)
(1)
Où λ, μ (Pa) sont les paramètres de Lamé, E est le tenseur de déformation, e est le tenseur de déformation volumétrique, Pi (Pa) est la pression du fluide interstitiel (I est la matrice d’identité). Des conditions stationnaires sont supposées pour la composante solide sous contrainte poroélastique, ce qui signifie que les composantes du tenseur de contrainte sont orthogonales, 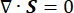 .
.
La figure 2 montre le système d’équations mathématiques mis en œuvre dans le modèle poroélastique décrit et l’interaction entre les composantes du modèle multiphysique présenté. Le flux de travail des simulations informatiques comprend :
Équations de problèmes électriques. La solution des équations du problème électrique fournit la source de chaleur RF Q (chauffage par effet Joule) moyennée dans le temps. À cette fin, une approximation quasi-statique des équations de Maxwell est utilisée pour calculer la distribution du champ électrique moyen dans le temps E (V/m) (Figure 2, bloc 1).
Équations de problèmes thermiques. La solution de l’équation de la biochaleur de Pennes (Figure 2, bloc 2) fournit la variation spatiale et temporelle de la température T (°C) résultant de la source de chaleur (Q) liée à l’énergie électromagnétique absorbée, de l’échauffement passif lié à la conduction thermique des tissus (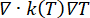 ), et de l’effet de dissipation thermique de la perfusion sanguine tissulaire (cWb(T) (T - Tb)). Le terme de dissipateur thermique se rapproche de l’échange de chaleur entre le sang circulant dans la microvascularisation et les tissus adjacents où la puissance électromagnétique est absorbée. L’équation de transfert de chaleur comprend également le terme d’advection (
), et de l’effet de dissipation thermique de la perfusion sanguine tissulaire (cWb(T) (T - Tb)). Le terme de dissipateur thermique se rapproche de l’échange de chaleur entre le sang circulant dans la microvascularisation et les tissus adjacents où la puissance électromagnétique est absorbée. L’équation de transfert de chaleur comprend également le terme d’advection (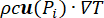 ), qui décrit le changement de température causé par le mouvement du liquide interstitiel à travers la matrice extracellulaire du modèle poroélastique. Cependant, ce terme a un impact négligeable sur le profil de température par rapport aux autres mécanismes responsables du changement de température.
), qui décrit le changement de température causé par le mouvement du liquide interstitiel à travers la matrice extracellulaire du modèle poroélastique. Cependant, ce terme a un impact négligeable sur le profil de température par rapport aux autres mécanismes responsables du changement de température.
Équations de problèmes de dynamique des fluides. L’équation de la conservation de la masse (Figure 2, bloc 3) combinée à la loi de Darcy (Figure 2, bloc 4) donne en sortie la variation spatiale et temporelle de la pression du fluide interstitiel Pirésultant de l’équilibre entre la source (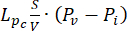 ) et le puits (
) et le puits (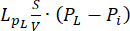 ) du fluide. Le terme de pression transitoire sur le membre gauche de l’équation de conservation de la masse,
) du fluide. Le terme de pression transitoire sur le membre gauche de l’équation de conservation de la masse, 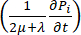 , décrit le réarrangement des composants fluides et solides dans le matériau poroélastique. Ceci est causé par la variation de la pression du liquide interstitiel, Pi, entraînée par la variation de la pression vasculaire Pven fonction de la température.
, décrit le réarrangement des composants fluides et solides dans le matériau poroélastique. Ceci est causé par la variation de la pression du liquide interstitiel, Pi, entraînée par la variation de la pression vasculaire Pven fonction de la température.
La différence entre la pression vasculaire (Pv) et la pression du liquide interstitiel (Pi) est la source du liquide qui circule à travers la matrice extracellulaire. Le terme sink est lié à la différence de pression entre les vaisseaux lymphatiques (PL) et l’espace interstitiel (Pi). Dans les tissus normaux, la pression dans le système vasculaire lymphatique (~ -6-0 mmHg) est jusqu’à deux fois inférieure à la pression du liquide interstitiel13. Cette différence de pression assure l’efficacité des vaisseaux lymphatiques à drainer l’excès de liquide qui s’échappe de la paroi des vaisseaux sanguins dans l’interstitium. Pour le modèle tumoral présenté ici, nous avons négligé la contribution du système lymphatique 4,16,22.
Les expressions mathématiques des équations (2) à (5) sont utilisées pour décrire la dépendance à la température de la conductivité électrique et thermique des tissus et de la perfusion sanguine tissulaire23,24. Deux modèles mathématiques différents sont utilisés pour décrire la dépendance de la température de la perfusion sanguine dans les domaines du tissu normal et du tissu tumoral, respectivement24,25. Les modèles montrent que la perfusion sanguine augmente avec la température jusqu’à neuf fois par rapport à la valeur de base dans le tissu normal et seulement environ deux fois la valeur de base dans le domaine tumoral. Pour les deux modèles, l’augmentation de la perfusion sanguine est limitée aux températures comprises dans la plage d’hyperthermie légère (inférieure à 45 °C). Il convient de mentionner que les expressions mathématiques, les équations (4) et (5), ne décrivent pas entièrement les mécanismes sous-jacents aux changements dépendants de la température dans la perfusion sanguine dans les deux types de tissus différents. Cependant, ils aident à représenter la perfusion limitée qui caractérise généralement le microenvironnement tumoral par rapport aux tissus normaux.
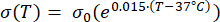 (2)
(2)
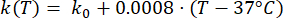 (3)
(3)
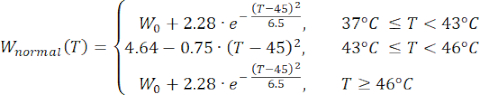 (4)
(4)
 (5)
(5)
 (6)
(6)
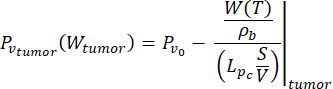 (7)
(7)
Dans cette étude, nous avons utilisé les équations (6) et (7) pour modéliser la pression vasculaire en fonction de la perfusion sanguine à la fois pour les modèles de tissus normaux et tumoraux26. À partir des équations (4) et (5), le débit sanguin peut être exprimé comme le rapport entre la perfusion sanguine et la densité sanguine. La relation entre le débit sanguin et la pression vasculaire est bien établie dans la littérature3 : le débit sanguin et la résistance géométrique (ou conductivité, Lp) du système vasculaire déterminent la différence de pression à l’intérieur du vaisseau sanguin. La pression vasculaire peut être exprimée en fonction de la température (équations (6) et (7)), en s’appuyant sur cette relation et sur le modèle de perfusion sanguine dépendant de la température (équations (4) et (5)).
La mise en œuvre du flux de travail de calcul (Figure 2) et les propriétés dépendantes de la température des modèles de tissus sont décrites en détail dans la section suivante. Toutes les propriétés des matériaux, ainsi que leurs descriptions et valeurs de référence (c.-à-d. à la température corporelle) sont énumérées dans le tableau 1. Voir la Table des matériaux pour plus de détails sur COMSOL Multiphysics installé sur un ordinateur utilisé pour implémenter ce protocole de calcul. Le problème électrique a été modélisé à l’aide du module AC/DC ; Le transfert de biochaleur a été modélisé à l’aide de la physique du transfert de chaleur ; et le problème de dynamique des fluides a été modélisé à l’aide de l’interface mathématiques.
Protocole
1. Construire le modèle d’un système de radiofréquence bipolaire
- Étapes préliminaires de configuration de l’interface
- Lancez COMSOL Multiphysics et cliquez sur Model Wizard.
- Sélectionnez 3D comme dimension spatiale.
- Sélectionnez le module de physique AC/DC | Champs et courants électriques | Courants électriques.
- Sélectionnez le module de transfert de chaleur | Transfert de chaleur dans les solides.
- Sélectionner le module Mathématiques | Interfaces PDE | Forme du coefficient PDE.
- Sélectionner une étude | En fonction du temps. Cliquez sur Terminé.
- Une fois que l’espace de travail Comsol apparaît :
- Sélectionnez Multiphysique | Chauffage électromagnétique. Avec cette étape, la densité de perte de puissance électromagnétique est automatiquement couplée comme source de chaleur pour l’équation de transfert de biochaleur.
REMARQUE : Si Multiphysics n’apparaît pas automatiquement, spécifiez manuellement la source de chaleur électromagnétique (affichée dans COMSOL sous forme de densité de perte volumétrique). Pour plus de détails sur l’ajout de la source de chaleur, voir la section 'Physique', étape 2 'Configuration du problème thermique'. - Sélectionnez Étude dans le ruban supérieur | Étapes de l’étude | Fréquence transitoire.
- Sélectionnez Multiphysique | Chauffage électromagnétique. Avec cette étape, la densité de perte de puissance électromagnétique est automatiquement couplée comme source de chaleur pour l’équation de transfert de biochaleur.
- Définissez les géométries. Dans le ruban supérieur, sélectionnez Géométrie, puis :
- Définissez deux cônes avec les dimensions indiquées dans le tableau 2.
- Positionnez les cônes à la distance indiquée dans le tableau 2 (espacés dentre les deux ). Ces deux cônes modéliseront les deux aiguilles hypodermiques utilisées pour la construction du système RF bipolaire.
- Dupliquer les deux cônes précédents pour modéliser l’isolation des aiguilles ; modifier la taille du cône en fonction des dimensions indiquées dans le tableau 2.
- Sélectionnez un cylindre (hauteur, hm et diamètre dm) pour modéliser la masse du muscle placé à z = - 9 mm (x = 0, y = 0). Les valeurs de chaque dimension sont répertoriées dans le tableau 2.
- Sélectionnez un cylindre (hauteur, hs et diamètre ds) pour modéliser la fine couche de peau placée à z = 4 mm (x = 0, y = 0). Les valeurs de chaque dimension sont répertoriées dans le tableau 2.
- Sélectionner une sphère (diamètre, dt) pour modéliser la tumeur sous-cutanée placée à z = -0,5 mm (x = 0, y = 0). La taille de la tumeur est indiquée dans le tableau 2.
- Pour faciliter la sélection des géométries dans les étapes suivantes du protocole, nous vous recommandons ce qui suit :
- Dans le ruban Géométrie , sélectionnez Opérations virtuelles | Former des domaines composites.
- Sélectionnez tous les domaines liés à la partie électriquement conductrice des aiguilles pour créer une géométrie composite.
- Répétez la même procédure pour créer des domaines composites pour les géométries d’isolation de l’aiguille.
- Définir les propriétés des modèles de tissus biologiques.
REMARQUE : Les étapes suivantes décrivent la procédure d’implémentation des expressions mathématiques décrites par les équations (2)-(7).- Dans le nœud Composant, cliquez avec le bouton droit de la souris pour sélectionner Définitions.
- Sous Fonctions, sélectionnez Analytique.
- Spécifiez le nom de la fonction (par exemple, k_muscle ou sigma_muscle) et tapez l’expression mathématique conformément à l’équation 2).
- Spécifiez la température (T) comme argument.
- Spécifiez les unités de la fonction : S/m dans le cas de la conductivité électrique.
- Répétez les étapes précédentes de 1 à 3 pour mettre en œuvre l’équation 3, en modifiant l’unité en conséquence (c’est-à-dire W/(m·K) pour la conductivité thermique).
- Spécifiez l’unité de l’argument : K (kelvin) pour la température. Dans Paramètres de tracé, spécifiez la plage de valeurs de l’argument de fonction (c’est-à-dire la température). Pour suivre ce protocole, utilisez une plage de 33 à 100 °C (306,15 à 373,15 K).
- Répétez les étapes précédentes de 1 à 5 pour ajouter les fonctions dépendantes de la température des conductivités électriques (équation 2) et thermiques (équation 3) pour chaque modèle de tissu (c’est-à-dire muscle, peau et tumeur) en utilisant les valeurs nominales répertoriées dans le tableau 1 (le tissu normal fait référence à la fois au muscle et à la peau).
- Sous Fonctions, sélectionnez Tronçon pour implémenter les équations (4)-(7) :
- Spécifiez le nom de la fonction.
- Spécifiez la température (T) comme argument de la fonction.
- Tapez l’expression mathématique pour chaque intervalle de température conformément aux équations (4) à (7).
- Répétez les étapes précédentes de 1 à 3 pour ajouter les fonctions dépendantes de la température de la perfusion sanguine et de la pression vasculaire pour chaque modèle de tissu en utilisant les valeurs nominales indiquées dans le tableau 1 (le tissu normal fait référence à la fois au muscle et à la peau).
- Attribuez des propriétés de matériau aux composants géométriques.
- Dans le noeud du composant, sélectionnez Matériaux.
- Sélectionnez les matériaux vierges pour inclure les tissus normaux, les tissus tumoraux, le sang, le PTFE et l’acier inoxydable.
- Activez la sélection manuelle et sélectionnez l’entité géométrique correspondant au matériau spécifié.
- Les tissus normaux sont associés à des géométries modelant les muscles et la peau.
- La tumeur et les tissus sanguins sont associés à la géométrie de la tumeur.
- Le matériau PTFE est associé aux géométries modélisant l’isolant de l’aiguille.
- Le matériau en acier inoxydable est associé aux géométries des cônes modélisant le sol et les aiguilles actives.
- Pour les conductivités électriques et thermiques dépendantes de la température 23, tapez le nom choisi de la fonction et l’argument associé (c’est-à-dire T) qui apparaît dans le nœud Définitions.
- Pour les propriétés du matériau qui ne dépendent pas de la température, reportez-vous aux valeurs de référence27 énumérées dans le tableau 1.
REMARQUE : Nous nous appuyons sur la théorie poroélastique pour calculer la pression 16,17,26. Les étapes suivantes montrent comment les propriétés d’un matériau poreux peuvent être attribuées à un domaine spécifique. - Dans Matériaux, sélectionnez Autres matériaux | Matériau poreux.
- Cliquez avec le bouton droit de la souris sur Matériau poreux pour sélectionner les composants Fluide et Solide . Sélectionnez Nœud Fluide et, sous Propriétés du fluide, sélectionnez Sang (défini dans les étapes précédentes). Sélectionnez Nœud solide et sous Propriétés solides, sélectionnez Tumeur (définie dans les étapes précédentes). Dans le nœud Solide, spécifiez la fraction volumique définie comme θS (Tableau 1).
- Activez la sélection manuelle et sélectionnez l’entité géométrique correspondant au matériau spécifié. Pour suivre ce protocole, supposons que seule la région tumorale est un domaine poroélastique.
- Maillage
- Sous Nœud de maillage, sélectionnez Taille et sélectionnez un maillage plus fin prédéfini.
- Ajout de la fonction tétraédrique libre sous le nœud Mesh . Cette étape permet d’obtenir un maillage raffiné dans les zones critiques.
REMARQUE : Pour ce modèle, nous avons identifié les bords de la tumeur et l’extrémité distale des modèles d’aiguille hypodermique comme des zones critiques. - Sélectionnez les géométries qui vous intéressent et personnalisez la taille maximale (0,25 mm) et minimale de l’élément de manière à ce que le plus petit composant (par exemple, la pointe de l’aiguille) soit discrétisé par au moins quatre éléments de maillage (le maillage complet se compose de 1 487 828 éléments).
2. Physique
- Configuration pour le problème électrique
REMARQUE : Les étapes suivantes fournissent des informations sur la façon de définir les paramètres de calcul de la distribution du champ électrique (Figure 2, bloc 1) qui fournira la source de chaleur radiofréquence (Q).- Faites un clic droit sur le nœud Courants électriques.
- Pour les conditions aux limites électriques illustrées à la figure 3A, sélectionnez Borne et Masse comme limites.
- Pour Terminal, sélectionnez manuellement l’extrémité proximale (en haut) de l’une des deux aiguilles. L’aiguille identifiée fournira la puissance d’entrée.
- Sous Terminal, sélectionnez Alimentation et spécifiez la valeur en fonction du protocole d’énergie souhaité. Pour suivre ce protocole, sélectionnez 0,5 W pour une hyperthermie légère sur la base d’expériences préliminaires ex vivo 20.
- Sélectionnez Sol et sélectionnez manuellement la surface proximale de la deuxième aiguille. Cette aiguille agira comme une électrode de retour pour le chemin de retour du courant électrique.
- Appliquez une isolation électrique sur la surface externe restante du modèle.
- Configuration pour le problème thermique
REMARQUE : Les étapes suivantes montrent comment inclure les fonctions de perfusion sanguine dépendantes de la température (équations 4 et 5) dans l’équation de transfert de biochaleur pour modéliser le dissipateur thermique causé par le flux sanguin.- Sélectionnez le nœud Transfert de chaleur dans les solides et spécifiez 33 °C comme valeur initiale de la température.
- Pour modéliser l’effet de dissipateur thermique dû au flux sanguin, cliquez avec le bouton droit de la souris sur Transfert de chaleur dans les solides, ajoutez le domaine Source de chaleur et sélectionnez la géométrie où l’effet de dissipateur thermique doit être pris en compte (c’est-à-dire la tumeur et le tissu normal ). Sélectionner Source générale | Défini par l’utilisateur où l’expression du dissipateur de chaleur peut être tapée.
- Pour les conditions limites thermiques illustrées à la figure 3B, cliquez avec le bouton droit de la souris sur Transfert de chaleur, ajoutez Flux de chaleur en tant que condition limite et spécifiez les surfaces externes auxquelles le flux de chaleur est appliqué. Sélectionnez Flux de chaleur convectif comme type de flux. Pour le coefficient de transfert de chaleur, utiliser h = 15 W/(m2 · K) de modéliser le mécanisme d’échange naturel de chaleur entre la peau et l’air28. Spécifiez la température extérieure. Utilisez T = 20 °C pour modéliser la température ambiante dans l’environnement du laboratoire.
- Configuration pour le problème de la dynamique des fluides
REMARQUE : Les étapes suivantes décrivent comment mettre en œuvre l’équation de conservation de la masse illustrée dans Graphique 2 (Bloc 3) et comment elle peut être liée à la variation de la température.- Sélectionnez le nœud Forme de coefficient PDE et spécifiez Pression comme variable dépendante. À ce stade, l’unité Pascal (Pa) est automatiquement attribuée.
REMARQUE : Une fois la simulation calculée, les résultats peuvent être affichés et/ou exportés à l’aide de l’unité de votre choix. Nous présentons les résultats en utilisant l’unité mmHg pour plus de cohérence avec la littérature (voir la section des résultats représentatifs). - Spécifiez l’unité de conductance fluide 1/s comme quantité du terme source.
- Définissez le nom pour identifier la variable (Pi, pression du fluide interstitiel dans cette étude).
- Cliquez avec le bouton droit de la souris sur le nœud Coefficient Form PDE et sélectionnez le domaine Coefficient Form . Spécifiez l’entité géométrique à laquelle l’équation se réfère (tumeur). Répétez les mêmes étapes et sélectionnez le tissu restant (tissu normal) sur lequel une EDP différente sera appliquée.
- Pour le modèle tumoral, spécifiez les coefficients et termes suivants pour obtenir l’équation de conservation de la masse (Figure 2 bloc 3) : coefficient de diffusion Kide la tumeur (Tableau 1) ; coefficient
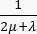 d’amortissement ); terme source
d’amortissement ); terme source 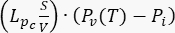 . Pour le modèle tumoral, négligez l’apport du système lymphatique. Définissez tous les autres coefficients égaux à zéro.
. Pour le modèle tumoral, négligez l’apport du système lymphatique. Définissez tous les autres coefficients égaux à zéro. - Pour le modèle de tissu normal, spécifiez les coefficients et les termes suivants pour obtenir l’équation de conservation de la masse (Figure 2 bloc 3) : coefficient de diffusion Ki du tissu normal (Tableau 1) ; coefficient
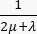 d’amortissement ; terme source
d’amortissement ; terme source 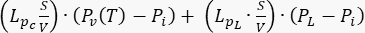 . Pour considérer un tissu normal comme un tissu fonctionnant normalement, considérez la contribution du système lymphatique. Définissez tous les autres coefficients égaux à zéro.
. Pour considérer un tissu normal comme un tissu fonctionnant normalement, considérez la contribution du système lymphatique. Définissez tous les autres coefficients égaux à zéro. - Pour faire le lien avec la simulation électromagnético-thermique, exprimez la pression vasculaire Pv en fonction de la température (au moyen de la variable de perfusion sanguine, voir équations 6 et 7).
- Cliquez avec le bouton droit de la souris sur Coefficient Form PDE et sélectionnez Valeurs initiales. Sélectionnez le domaine géométrique (tumeur) et répétez la même étape pour le modèle de tissu normal (tissu normal). Spécifiez Pi0pour la tumeur et les tissus normaux selon les valeurs énumérées dans le tableau 1.
- Pour les conditions aux limites liées à l’étude de la dynamique des fluides, illustrées à la figure 3C, cliquez avec le bouton droit de la souris sur Forme du coefficient PDE et sélectionnez Conditions aux limites de Dirichlet. Sélectionnez la surface externe du domaine du tissu normal et attribuez la valeur Pi0correspondant au tissu normal (tableau 1).
- Sélectionnez le nœud Forme de coefficient PDE et spécifiez Pression comme variable dépendante. À ce stade, l’unité Pascal (Pa) est automatiquement attribuée.
3. Exécutez les simulations et affichez les résultats
REMARQUE : Comme dernière étape avant le calcul, spécifiez le temps (simulant la durée de la procédure) et la fréquence de fonctionnement :
- Sélectionnez Transitoire de fréquence dans le nœud Étude.
- Spécifiez la ou les unité(s) de temps.
- Dans Temps de sortie, sélectionnez plage (sur le côté droit) et spécifiez 0 s comme début, 5 s comme pas et 900 s comme arrêt.
- Réglez la fréquence sur 500E3 Hz.
- Sélectionnez Calculer pour exécuter les simulations.
- Pour la visualisation des résultats, sélectionnez Jeux de données sous le nœud Résultats.
- Cliquez avec le bouton droit de la souris pour sélectionner un plan de coupe afin de définir le plan à utiliser pour visualiser les distributions 2D (par exemple, zx-plan à y = 0).
- Cliquez avec le bouton droit de la souris pour sélectionner un point de coupe dans le volume 3D afin d’afficher la variation d’un paramètre dans le temps.
- À partir des résultats sur le ruban supérieur,
- Sélectionnez le groupe de tracés 2D pour visualiser la distribution bidimensionnelle d’une variable (par exemple, la température) sur l’un des plans identifiés dans les étapes ci-dessus.
- Sélectionnez le groupe de tracés 1D pour visualiser les résultats 1D (par exemple, la pression dans le temps) au point ou à plusieurs points identifiés dans les étapes ci-dessus.
REMARQUE : Le temps nécessaire pour exécuter les simulations avec les paramètres décrits dans ce protocole est d’environ 2,5 h.
Résultats
La distribution homogène d’une pression de fluide interstitielle élevée au sein de la tumeur et une chute vers les valeurs normales (0-3 mmHg) à la périphérie sont des caractéristiques de l’EUT. Les figures 4 et 5 montrent les conditions initiales (t = 0 min) de la température (A), de la pression du fluide interstitiel (B) et de la vitesse du fluide (C). Avant de commencer le chauffage, lorsque la température initiale est de 33 °C, la valeur de la ...
Discussion
Nous présentons un protocole de modélisation informatique pour coupler des simulations électro-thermiques transitoires avec des simulations de dynamique des fluides afin d’étudier l’impact de l’hyperthermie RF sur les profils de pression des fluides thermiques et interstitiels dans les tumeurs. L’aspect clé réside dans la construction d’un flux de travail numérique capable de capturer la relation existant entre la température et la pression vasculaire, qui à son tour entraîne les changements de pressi...
Déclarations de divulgation
Les auteurs n’ont aucun conflit d’intérêts à divulguer.
Remerciements
L’étude a été soutenue par des subventions de la National Science Foundation (n° 2039014) et de l’Institut national du cancer (R37CA269622).
matériels
| Name | Company | Catalog Number | Comments |
| COMSOL Multiphysics (v. 6.0) | COMSOL AB, Stockholm, Sweden | Software used to implement the computational workflow described in the protocol | |
| Dell 1.8.0, 11th Gen Intel(R) Core(TM) i7-11850H @ 2.50GHz, 2496 Mhz, 8 Core(s), 16 Logical Processor(s), 32 GB RAM | Dell Inc. | Laptop used to run computational simulations |
Références
- Nia, H. T., Munn, L. L., Jain, R. K. Physical traits of cancer. Science. 370 (6516), 546-556 (2020).
- Heldin, C. -. H., Rubin, K., Pietras, K., Östman, A. High interstitial fluid pressure - an obstacle in cancer therapy. Nature Reviews Cancer. 4 (10), 806-813 (2004).
- Jain, R. K. Determinants of tumor blood flow: a review. Cancer Research. 48, 2641-2658 (1988).
- Stylianopoulos, T., Munn, L. L., Jain, R. K. Reengineering the physical microenvironment of tumors to improve drug delivery and efficacy: from mathematical modeling to bench to bedside. Trends in Cancer. 4 (4), 292-319 (2018).
- Sheth, R. A., Hesketh, R., Kong, D. S., Wicky, S., Oklu, R. Barriers to drug delivery in interventional oncology. Journal of Vascular and Interventional Radiology. 24 (8), 1201-1207 (2013).
- Chauhan, V. P., Stylianopoulos, T., Boucher, Y., Jain, R. K. Delivery of molecular and nanoscale medicine to tumors: transport barriers and strategies. Annual Review of Chemical and Biomolecular Engineering. 2 (1), 281-298 (2011).
- Li, R., et al. Interstitial flow promotes macrophage polarization toward an M2 phenotype. Molecular Biology of the Cell. 29 (16), 1927-1940 (2018).
- Stine, C. A., Munson, J. M. Autologous gradient formation under differential interstitial fluid flow environments. Biophysica. 2 (1), 16-33 (2022).
- Provenzano, P. P., et al. Enzymatic targeting of the stroma ablates physical barriers to treatment of pancreatic ductal adenocarcinoma. Cancer Cell. 21 (3), 418-429 (2012).
- Pal, K., Sheth, R. A. Engineering the tumor immune microenvironment through minimally invasive interventions. Cancers. 15 (1), 196 (2022).
- Dunne, M., Regenold, M., Allen, C. Hyperthermia can alter tumor physiology and improve chemo- and radio-therapy efficacy. Advanced Drug Delivery Reviews. 163-164, 98-124 (2020).
- Vaupel, P., et al. From localized mild hyperthermia to improved tumor oxygenation: physiological mechanisms critically involved in oncologic thermo-radio-immunotherapy. Cancers. 15 (5), 1394 (2023).
- Stapleton, S., et al. Radiation and heat improve the delivery and efficacy of nanotherapeutics by modulating intratumoral fluid dynamics. ACS Nano. 12 (8), 7583-7600 (2018).
- Li, Q., Zhou, Y., Zhang, F., McGregor, H., Yang, X. Radiofrequency hyperthermia enhances locally delivered oncolytic immuno-virotherapy for pancreatic adenocarcinoma. CardioVascular and Interventional Radiology. 45 (12), 1812-1821 (2022).
- Mpekris, F., et al. Combining microenvironment normalization strategies to improve cancer immunotherapy. Proceedings of the National Academy of Sciences. 117 (7), 3728-3737 (2020).
- Netti, P. A., Baxter, L. T., Boucher, Y., Skalak, R., Jam, R. K. Time-dependent behavior of interstitial fluid pressure in solid tumors: implications for drug delivery. Cancer Research. 15 (55), 5451-5458 (1995).
- Andreozzi, A., Iasiello, M., Netti, P. A. Effects of pulsating heat source on interstitial fluid transport in tumour tissues. Journal of The Royal Society Interface. 17 (170), 612-626 (2020).
- Leunig, M., Goetz, A. E., Messmer, K. Interstitial fluid pressure in solid tumors following hyperthermia: possible correlation with therapeutic response. Cancer Research. 52, 487-490 (1992).
- Muñoz, N. M., et al. Immune modulation by molecularly targeted photothermal ablation in a mouse model of advanced hepatocellular carcinoma and cirrhosis. Scientific Reports. 12 (1), 14449 (2022).
- Bottiglieri, A., et al. RF-hyperthermia to modulate tumor interstitial fluid pressure: an in vivo pilot study. 38th Annual Society for Thermal Medicine Meeting. , (2023).
- Baxter, L. T., Jain, R. K. Transport of fluid and macromolecules in tumors. I. Role of interstitial pressure and convection. Microvascular Research. 37 (1), 77-104 (1989).
- Stapleton, S., et al. A mathematical model of the enhanced permeability and retention effect for liposome transport in solid tumors. PLoS ONE. 8 (12), 1-10 (2013).
- Rossmann, C., Haemmerich, D. Review of temperature dependence of thermal properties, dielectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures. Critical Reviews in Biomedical Engineering. 42 (6), 467-492 (2014).
- Song, C. W., Lokshina, A., Rhee, J. G., Patten, M., Levitt, S. H. Implication of blood flow in hyperthermic treatment of tumors. IEEE Transactions on Biomedical Engineering. 31 (1), 9-16 (1984).
- Tompkins, D. T., et al. Temperature-dependent versus constant-rate blood perfusion modelling in ferromagnetic thermoseed hyperthermia: results with a model of the human prostate. International Journal of Hyperthermia. 10 (4), 517-536 (1994).
- Andreozzi, A., Iasiello, M., Netti, P. A. A thermoporoelastic model for fluid transport in tumour tissues. Journal of The Royal Society Interface. 16 (154), 0030-0046 (2019).
- Hasgall, P. A., et al. . IT'IS Database for thermal and electromagnetic parameters of biological tissues. , (2022).
- Cavagnaro, M., et al. Influence of the target tissue size on the shape of ex vivo microwave ablation zones. International Journal of Hyperthermia. 31 (1), 48-57 (2015).
- Munson, J., Shieh, A. Interstitial fluid flow in cancer: implications for disease progression and treatment. Cancer Management and Research. 19 (6), 317-328 (2014).
- Muñoz, N. M., et al. Influence of injection technique, drug formulation and tumor microenvironment on intratumoral immunotherapy delivery and efficacy. Journal for ImmunoTherapy of Cancer. 9 (2), 0018-0027 (2021).
- Swartz, M. A., Lund, A. W. Lymphatic and interstitial flow in the tumour microenvironment: linking mechanobiology with immunity. Nature Reviews Cancer. 12 (3), 210-219 (2012).
- Mehta, A., Oklu, R., Sheth, R. A. Thermal ablative therapies and immune checkpoint modulation: can locoregional approaches effect a systemic response. Gastroenterology Research and Practice. 2016, 1-11 (2016).
- Song, C. W., Park, H., Griffin, R. J. Improvement of tumor oxygenation by mild hyperthermia. Radiation Research. 155 (4), 515-528 (2001).
- Dewhirst, M. W., Oleson, J. R., Kirkpatrick, J., Secomb, T. W. Accurate three-dimensional thermal dosimetry and assessment of physiologic response are essential for optimizing thermoradiotherapy. Cancers. 14 (7), 1701 (2022).
Réimpressions et Autorisations
Demande d’autorisation pour utiliser le texte ou les figures de cet article JoVE
Demande d’autorisationThis article has been published
Video Coming Soon