Quantitative Strain Mapping of an Abdominal Aortic Aneurysm

Source: Hannah L. Cebull¹, Arvin H. Soepriatna¹, John J. Boyle² and Craig J. Goergen¹

¹Weldon School of Biomedical Engineering, Purdue University, West Lafayette, Indiana

²Mechanical Engineering & Materials Science, Washington University in St. Louis, St Louis, Missouri

The mechanical behavior of soft tissues, such as blood vessels, skin, tendons, and other organs, are strongly influenced by their composition of elastin and collagen, which provide elasticity and strength. The fiber orientation of these proteins depends on the type of soft tissue and can range from a single preferred direction to intricate meshed networks, which can become altered in diseased tissue. Therefore, soft tissues often behave anisotropically on the cellular and organ level, creating a need for three-dimensional characterization. Developing a method for reliably estimating strain fields within complex biological tissues or structures is important to mechanically characterize and understande disease. Strain represents how soft tissue relatively deforms over time, and it can be described mathematically through various estimations.

Acquiring image data over time allows deformation and strain to be estimated. However, all medical imaging modalities contain some amount of noise, which increases the difficulty of accurately estimating in vivo strain. The technique described here successfully overcomes these issues by using a direct deformation estimation (DDE) method to calculate spatially varying 3D strain fields from volumetric image data.

Current strain estimation methods include digital image correlation (DIC) and digital volume correlation. Unfortunately, DIC can only accurately estimate strain from a 2D plane, severely limiting the application of this method. While useful, 2D methods such as DIC have difficulty quantifying strain in regions that undergo 3D deformation. This is because out-of-plane motion creates deformation errors. Digital volume correlation is a more applicable method that divides the initial volume data into regions and finds the most similar region of the deformed volume, thereby reducing out-of-plane error. However, this method proves to be sensitive to noise and requires assumptions about the mechanical properties of the material.

The technique demonstrated here eliminates these issues by using a DDE method, thus making it very useful in the analysis of medical imaging data. Furthermore, it is robust to high or localized strain. Here we describe the acquisition of gated, volumetric 4D ultrasound data, its conversion into an analyzable format, and the use of a custom Matlab code to estimate 3D deformation and corresponding Green-Lagrange strains, a parameter that better describes large deformations. The Green-Lagrange strain tensor is implemented in many 3D strain estimation methods because it allows for F to be calculated from a Least Squares Fit (LSF) of the displacements. The equation below represents the Green-Lagrange strain tensor, E, where F and I represent the deformation gradient and second order identity tensor, respectively.

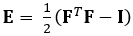(1)