The pH of a salt solution is determined by its component anions and cations. Salts that contain pH-neutral anions and the hydronium ion-producing cations form a solution with a pH less than 7. For example, in ammonium nitrate (NH₄NO₃) solution, NO₃⁻ ions do not react with water whereas NH₄⁺ ions produce the hydronium ions resulting in the acidic solution. In contrast, salts that contain pH-neutral cations and the hydroxide ion-producing anions form a solution with a pH greater than 7. For example, in sodium fluoride (NaF) solution, the Na⁺ is pH-neutral but the F^- produces the hydroxide ions and forms the basic solution. The counterions of a strong acid or base are pH-neutral and salts formed by such counterions form a neutral solution with a pH equal to 7. For example, in KBr, The K⁺ cation is inert and will not affect pH. The bromide ion is the conjugate base of a strong acid, and so it is of negligible base strength (no appreciable base ionization). The solution is neutral.

Some salts contain both an acidic cation and a basic anion. The overall acidity or basicity of a solution is determined by the relative strength of the cation and anion, which can be compared using K_a and K_b. For example, in NH₄F, the NH₄⁺ ion is acidic and the F⁻ ion is basic (conjugate base of the weak acid HF). Comparing the two ionization constants: K_a of NH₄⁺ is 5.6 × 10⁻¹⁰ and the K_b of F⁻ is 1.6× 10⁻¹¹, so the solution is acidic, since K_a > K_b.

Calculating the pH of an Acidic Salt Solution

Aniline is an amine that is used to manufacture dyes. It is isolated as anilinium chloride, [C₆H₅NH₃⁺]Cl, a salt prepared by the reaction of the weak base aniline and hydrochloric acid. What is the pH of a 0.233 M solution of anilinium chloride?

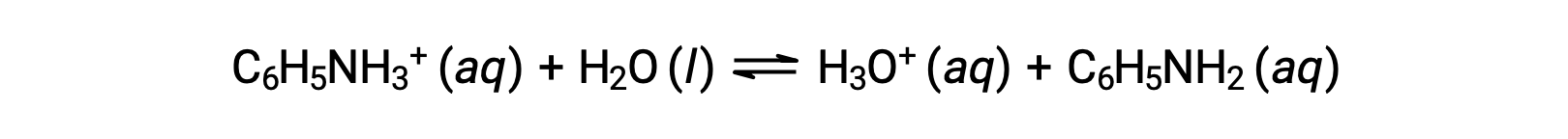
The K_a for anilinium ion is derived from the K_b for its conjugate base, aniline:

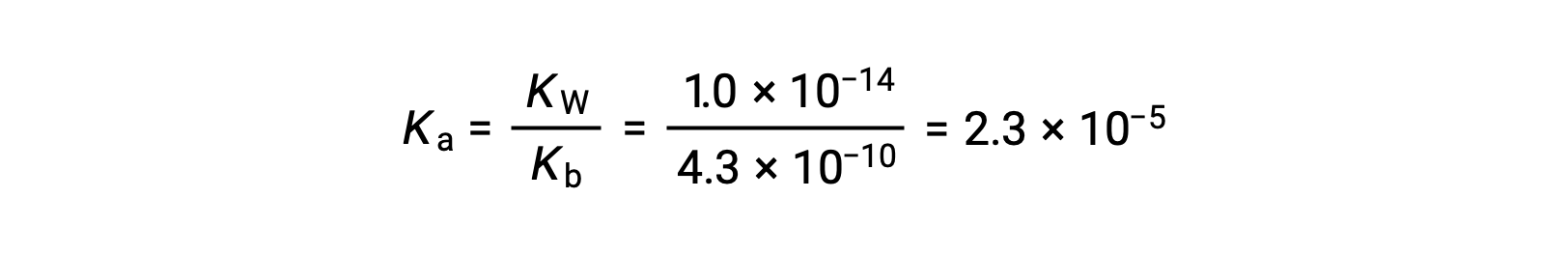
Using the provided information, an ICE table for this system is prepared:

	C6H5NH3+ (aq)	H3O+ (aq)	C6H5NH2 (aq)
Initial Concentration (M)	0.233	~0	0
Change (M)	−x	+x	+x
Equilibrium Concentration (M)	0.233 − x	x	x

Substituting these equilibrium concentration terms into the K_a expression gives

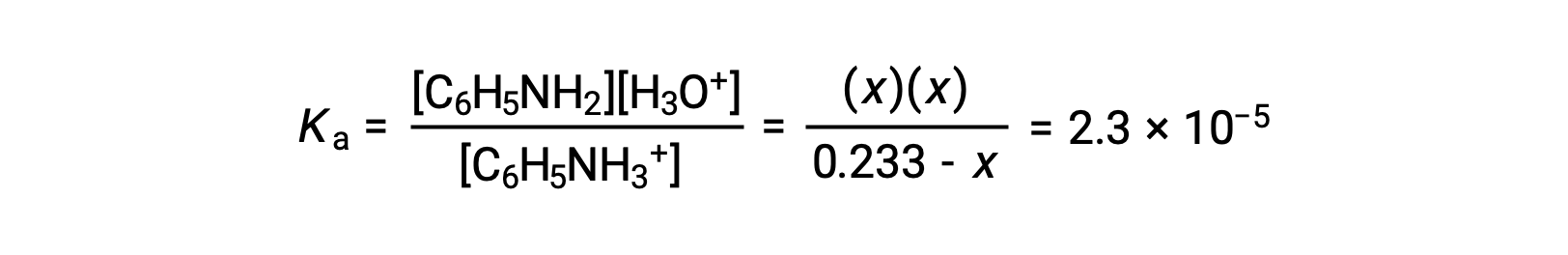
Assuming x << 0.233, the equation is simplified and solved for x:

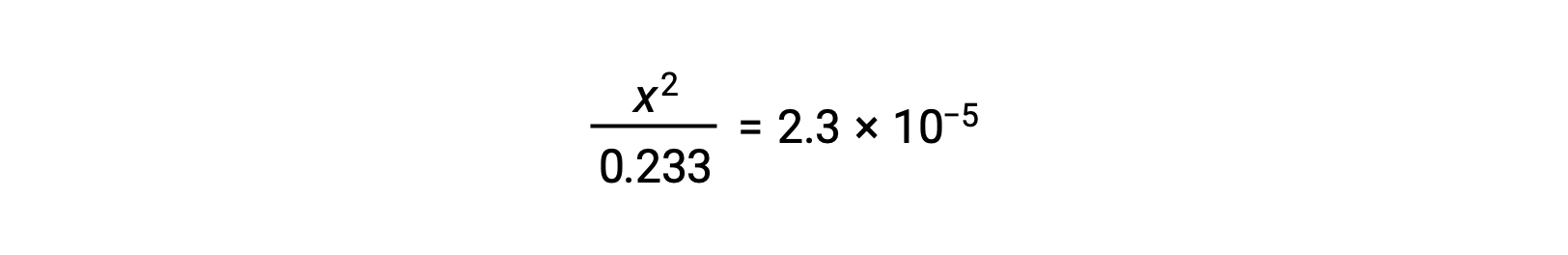
The ICE table defines x as the hydronium ion molarity, and so the pH is computed as

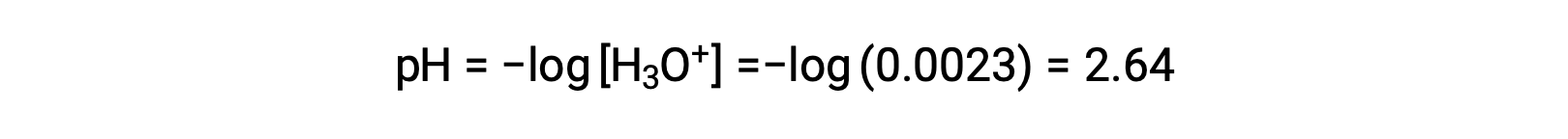
Hydrolysis of [Al(H₂O)₆]³⁺

Calculate the pH of a 0.10 M solution of aluminum chloride, which dissolves completely to give the hydrated aluminum ion [Al(H₂O)₆]³⁺ in solution.

The equation for the reaction and K_a are:

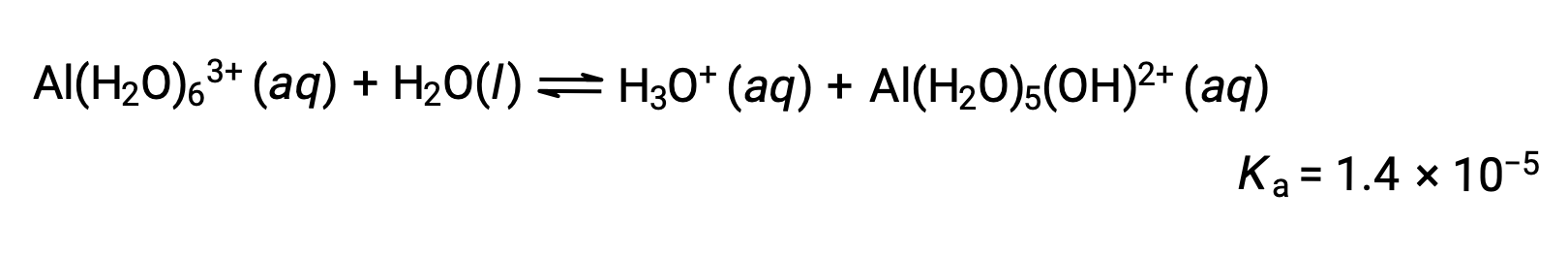
An ICE table with the provided information is

	Al(H2O)63+ (aq)	H3O+ (aq)	Al(H2O)5(OH)2+ (aq)
Initial Concentration (M)	0.10	~0	0
Change (M)	−x	+x	+x
Equilibrium Concentration (M)	0.10 − x	x	x

Substituting the expressions for the equilibrium concentrations into the equation for the ionization constant yields:

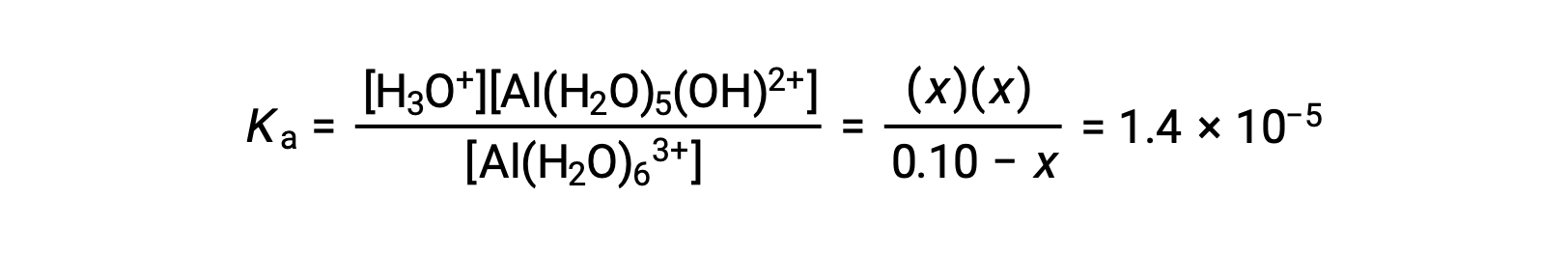
Assuming x << 0.10 and solving the simplified equation gives:

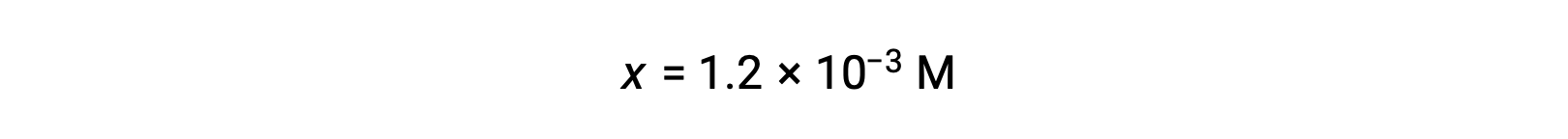
The ICE table defined x as equal to the hydronium ion concentration, and so the pH is calculated to be 2.92, and the solution is acidic.

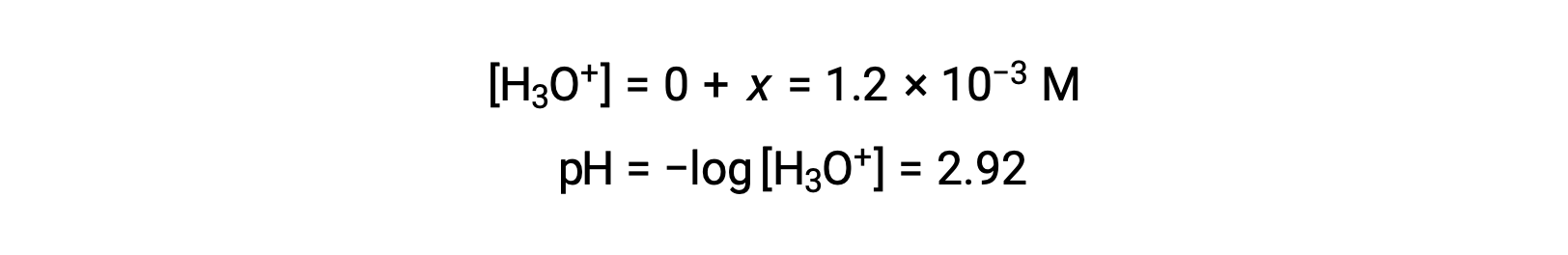
This text is adapted from Openstax, Chemistry 2e, Section 14.4: Hydrolysis of Salts.