10.10 : Moment of Inertia of Compound Objects
The moment of inertia is a quantitative measure of the rotational inertia of an object. It is defined as the sum of the products obtained by multiplying the mass of each particle of matter in a given body by the square of its distance from the axis. The total moment of inertia for compound objects can be found by determining and adding the moment of inertia of individual components together.
Consider a child of mass (mc) 25 kg standing at a distance (rc) of 1 m from the axis of a rotating merry-go-round. The merry-go-round is approximated as a uniform solid disk with a mass (mm) of 500 kg and a radius (rm) of 2 m. Find the moment of inertia of the compound system.
The total moment of inertia of the system can be determined by adding up the individual moments of inertia of the merry-go-round and the child rotating on the axis. Since the mass and size of the child are much smaller than the merry-go-round, the child can be considered as a point mass.
- The moment of inertia (I) for the child is calculated as
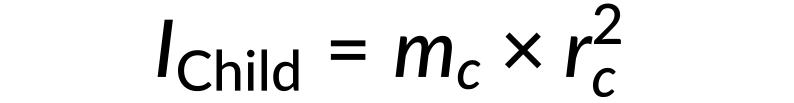
- The moment of inertia (I) for the merry-go-round is calculated as
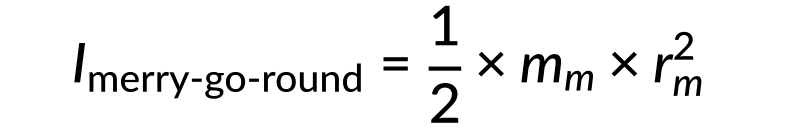
- By substituting and adding both values, the total moment of inertia of the system is determined to be 1025 kg⋅m2.
This text is adapted from Openstax, University Physics Volume 1, Section 10.5: Calculating Moments of Inertia.
From Chapter 10:

Now Playing
10.10 : Moment of Inertia of Compound Objects
Rotation and Rigid Bodies
6.1K Views

10.1 : Angular Velocity and Displacement
Rotation and Rigid Bodies
14.8K Views

10.2 : Angular Velocity and Acceleration
Rotation and Rigid Bodies
8.8K Views

10.3 : Rotation with Constant Angular Acceleration - I
Rotation and Rigid Bodies
6.6K Views

10.4 : Rotation with Constant Angular Acceleration - II
Rotation and Rigid Bodies
5.9K Views

10.5 : Relating Angular And Linear Quantities - I
Rotation and Rigid Bodies
6.5K Views

10.6 : Relating Angular And Linear Quantities - II
Rotation and Rigid Bodies
5.4K Views

10.7 : Moment of Inertia
Rotation and Rigid Bodies
11.9K Views

10.8 : Moment of Inertia and Rotational Kinetic Energy
Rotation and Rigid Bodies
7.2K Views

10.9 : Moment of Inertia: Calculations
Rotation and Rigid Bodies
6.7K Views

10.11 : Parallel-axis Theorem
Rotation and Rigid Bodies
6.4K Views

10.12 : Perpendicular-Axis Theorem
Rotation and Rigid Bodies
2.6K Views

10.13 : Vector Transformation in Rotating Coordinate Systems
Rotation and Rigid Bodies
1.4K Views

10.14 : Coriolis Force
Rotation and Rigid Bodies
3.0K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved