JoVE Logo
Authors
Contact Us

Sign In

A subscription to JoVE is required to view this content. Sign in or start your free trial.

In This Article

  • Summary
  • Abstract
  • Introduction
  • Protocol
  • النتائج
  • Discussion
  • Disclosures
  • Acknowledgements
  • Materials
  • References
  • Reprints and Permissions

Summary

الهدف من هذا البروتوكول هو الكشف عن الديناميكيات الهيكلية لنشر البروتين أحادي البعد على طول الحمض النووي ، باستخدام عامل النسخ النباتي WRKY مجال البروتين كنظام مثالي. للقيام بذلك ، تم تنفيذ كل من محاكاة الديناميكا الجزيئية الذرية والحبيبات الخشنة جنبا إلى جنب مع عينات حسابية واسعة النطاق.

Abstract

يعد انزلاق بروتين عامل النسخ أحادي البعد (1-D) على طول الحمض النووي ضروريا لتسهيل انتشار TF لتحديد موقع الحمض النووي المستهدف للتنظيم الجيني. لا يزال اكتشاف دقة الزوج الأساسي (bp) لانزلاق TF أو الدوس على الحمض النووي أمرا صعبا من الناحية التجريبية. لقد أجرينا مؤخرا محاكاة الديناميكا الجزيئية لجميع الذرات (MD) لالتقاط خطوة عفوية 1-bp لبروتين TF صغير في مجال WRKY على طول الحمض النووي. استنادا إلى مسار خطوة WRKY 10 μs الذي تم الحصول عليه من عمليات المحاكاة هذه ، يوضح البروتوكول هنا كيفية إجراء عينات توافقية أكثر شمولا لأنظمة TF-DNA ، من خلال بناء نموذج حالة ماركوف (MSM) لخطوة البروتين 1-bp ، مع اختبار أعداد مختلفة من الحالات الدقيقة والكلية لبناء MSM. من أجل فحص البحث العملي 1-D المنتشر لبروتين TF جنبا إلى جنب مع الحمض النووي مع الأساس الهيكلي ، يوضح البروتوكول أيضا كيفية إجراء محاكاة MD ذات الحبيبات الخشنة (CG) لأخذ عينات من ديناميكيات النطاق طويل الأمد للنظام. مثل هذه النمذجة والمحاكاة CG مفيدة بشكل خاص للكشف عن التأثيرات الكهروستاتيكية للبروتين والحمض النووي على الحركات المنتشرة العملية لبروتين TF فوق عشرات الميكروثانية ، مقارنة بحركات خطوة البروتين دون الميكروثانية إلى الميكروثانية التي تم الكشف عنها من عمليات محاكاة جميع الذرات.

Introduction

عوامل النسخ (TF) تبحث عن الحمض النووي المستهدف لربط وتنظيم النسخ الجيني والأنشطة ذات الصلة1. بصرف النظر عن الانتشار ثلاثي الأبعاد (3D) ، فقد اقترح أن الانتشار الميسر ل TF ضروري للبحث عن الحمض النووي المستهدف ، حيث يمكن للبروتينات أيضا الانزلاق أو القفز على طول الحمض النووي أحادي البعد (1D) ، أو القفز مع النقل بين القطاعات على الحمض النووي2،3،4،5،6،7.

في دراسة حديثة ، أجرينا عشرات الميكروثانية (μs) محاكاة الديناميكا الجزيئية لتوازن الذرة بالكامل (MD) على نبات TF - بروتين مجال WRKY على الحمض النووي8. تم التقاط خطوة كاملة 1-bp من WRKY على الحمض النووي poly-A في غضون ميكروثانية. وقد لوحظت حركات البروتين على طول أخدود الحمض النووي وديناميكيات إصلاح الروابط الهيدروجينية (HBs). في حين أن مثل هذا المسار يمثل مسارا واحدا تم أخذ عينات منه ، إلا أن المشهد العام لخطوات البروتين لا يزال غير موجود. هنا ، نوضح كيفية توسيع العينات الحسابية حول مسار خطوة البروتين الذي تم التقاطه في البداية باستخدام نموذج حالة ماركوف (MSM) ، والذي تم تنفيذه على نطاق واسع لمحاكاة مجموعة متنوعة من الأنظمة الجزيئية الحيوية التي تنطوي على تغييرات تكوينية كبيرة وفصل على نطاق زمني9،10،11،12،13،14،15،16 ، 17,18,19. والغرض من ذلك هو الكشف عن المجموعة التوافقية والحالات المستقرة ميتا لنشر بروتين TF على طول الحمض النووي لخطوة دورية واحدة.

في حين أن محاكاة MD المذكورة أعلاه تكشف عن الدقة الذرية لحركات البروتين ل 1 نقطة أساس على الحمض النووي ، فإن الديناميكيات الهيكلية للانتشار العملي طويل الأمد ل TF على طول الحمض النووي بنفس الدقة العالية يصعب الوصول إليها. ومع ذلك ، فإن إجراء عمليات محاكاة MD ذات الحبيبات الخشنة (CG) على مستوى البقايا أمر سهل من الناحية الفنية. يمكن توسيع النطاق الزمني لمحاكاة CG بشكل فعال إلى عشرات أو مئات المرات أطول من المحاكاة الذرية 20،21،22،23،24،25،26،27،28،29. هنا ، نعرض محاكاة CG التي أجريت من خلال تنفيذ برنامج CafeMol الذي طوره مختبر تاكادا30.

في البروتوكول الحالي ، نقدم المحاكاة الذرية لبروتين مجال WRKY على طول الحمض النووي poly-A وبناء MSM أولا ، والتي تركز على أخذ عينات من حركات البروتين المتدرجة ل 1 نقطة أساس فقط على طول الحمض النووي. ثم نقدم نمذجة CG ومحاكاة نفس نظام البروتين والحمض النووي ، والتي توسع أخذ العينات الحسابية إلى الانتشار العملي للبروتين على مدى عشرات من نقاط أساس على طول الحمض النووي.

هنا ، نستخدم برنامج GROMACS 31,32,33 لإجراء محاكاة MD و MSMbuilder 34 لبناء MSM للقطات المطابقة للعينات ، وكذلك لاستخدام VMD 35 لتصور الجزيئات الحيوية. يتطلب البروتوكول أن يكون المستخدم قادرا على تثبيت البرنامج أعلاه وتنفيذه. ثم يعد تثبيت وتنفيذ برنامج CafeMol30 ضروريا لإجراء عمليات محاكاة CG MD. كما يتم إجراء المزيد من التحليلات للمسارات والتصور في VMD.

Protocol

1. بناء نموذج حالة ماركوف (MSM) من محاكاة MD الذرية

  1. مسار خطوة البروتين التلقائي وجمع الهياكل الأولية
    1. استخدم مسار MD 8 لجميع الذرات الذي تم الحصول عليه مسبقا 10-μs لاستخراج 10000 إطار بالتساوي من مسار خطوة "أمامي" 1-bp (أي إطار واحد لكل نانو ثانية). يجب أن يكون العدد الإجمالي للإطارات كبيرا بما يكفي ليشمل جميع التشكيلات التمثيلية.
    2. قم بإعداد مسار الانتقال باستخدام 10000 إطار في VMD بالنقر فوق ملف > حفظ الإحداثيات، اكتب البروتين أو النواة في مربع الذرات المحددة واختر الإطارات في مربع الإطارات، انقر حفظ للحصول على الإطارات المطلوبة.
      ملاحظة: تم استخدام مسار محاكاة MD لجميع الذرات الذي تم الحصول عليه مسبقا 10 ميكروثانية (يسمى "مسار الخطوة الأمامية" هنا) ل WRKY يخطو مسافة 1-bp على 34-bp متجانس poly-A DNA8 كمسار أولي لإطلاق المزيد من العينات التوافقية. لاحظ أنه في معظم الممارسات ، ومع ذلك ، يتم إنشاء مسار أولي ، من خلال إجراء محاكاة MD الموجهة أو المستهدفة ، أو تنفيذ طرق توليد المسار العامة ، وما إلى ذلك 36،37،38،39.
    3. قم بمحاذاة المحور الطويل للحمض النووي المرجعي (من البنية البلورية) إلى المحور x، واضبط مركز الكتلة الأولي (COM) للحمض النووي الكامل 34-bp في أصل مساحة الإحداثيات لراحة مزيد من تحليل البيانات. للقيام بذلك، انقر فوق ملحقات > وحدة تحكم Tk في VMD، واكتب في إطار الأمر وحدة تحكم Tk :
      المصدر rotate.tcl
      يمكن العثور على البرنامج النصي tcl في الملف التكميلي 3.
    4. ثم احسب الجذر والمتوسط والمربع المسافة (RMSD) للعمود الفقري للبروتين عن طريق محاذاة الحمض النووي المركزي 10 نقاط أساس (A 14 إلى 23 و T 14 إلى 23 بوصة) مع ذلك من البنية البلورية40 ، ويمثل RMSD المقاييس الهندسية للأنظمة (انظر الشكل 1A). قم بذلك بالنقر فوق ملحقات > VMD > تحليل > أداة مسار RMSD واكتب النواة والبقايا من 14 إلى 23 ومن 46 إلى 55 في مربع تحديد الذرة ، انقر فوق محاذاة ثم مربع RMSD لحساب قيم RMSD.
    5. حساب درجة دوران البروتين حول الحمض النووي Θ(t) على المستوى y-z في MATLAB عن طريق كتابة الأمر
      rad2deg(atan(z/y))
      مع تحديد الموقع الزاوي الأولي على أنه Θ (0) = 0 ، كما تم إجراؤه سابقا8.
    6. اكتب الأمر التالي في MATLAB41 لاستخدام أساليب K-means42,43,44 وتصنيف هياكل 10000 إلى 25 مجموعة عن طريق الكتابة:
      [idx, C]=kmeans( X, 25)
      هنا X هو مصفوفة 2D من RMSD وزاوية دوران WRKY على الحمض النووي. اجمع هياكل هذه المراكز العنقودية ال 25 لمزيد من عمليات محاكاة MD.
      ملاحظة: نظرا لأن البروتين RMSD الذي تم أخذ عينات منه بالنسبة إلى الحمض النووي يغطي نطاقا يبلغ حوالي 25 Å ، فإننا نختار 25 مجموعة للحصول على مجموعة واحدة لكل أنغستروم.
  2. إجراء الجولة 1من محاكاة MD وإعدادات المحاكاة
    1. بناء أنظمة ذرية للهياكل ال 25 باستخدام برنامج GROMACS 5.1.232 تحت حقل قوة parmbsc145 وباستخدام ملف buildsystem.sh من الملف التكميلي 2 في shell.
    2. قم بإجراء محاكاة MD 60-ns لهذه الأنظمة ال 25 تحت مجموعة NPT بخطوة زمنية تبلغ 2 fs عن طريق كتابة الأمر التالي في shell:
      gmx_mpi grompp -f md.mdp -c npt.gro -p topol.top -o md.tpr
      gmx_mpi mdrun -deffnm md
  3. تجميع الرقم 1سانت مسارات MD المستديرة
    1. قم بإزالة أول 10 نانو ثانية من كل مسار محاكاة عن طريق الكتابة في shell:
      gmx_mpi trjcat -f md.xtc -b 10000 -e 600000 -o newtraj.xtc
      وجمع التكوينات من مسارات 25 × 50 ns للتجميع لإعداد هياكل المدخلات لأخذ العينات اللاحقة الأكثر شمولا (محاكاة MD الجولةالثانية ).
      ملاحظة: لتقليل التأثير من المسار الأولي وللسماح بالتوازن المحلي، تمت إزالة 10-ns من الفترة الأولية للمحاكاة.
    2. اختر أزواج المسافة بين البروتين والحمض النووي كمعلمات إدخال لتحليل المكونات المستقلة عن الوقت (tICA) 46،47،48 الإسقاط. استخدم الأمر make_ndx في غروماكس للقيام بما يلي:
      gmx_mpi make_ndx -f input.pdb -o index.ndx
      ملاحظة: هنا ، تم اختيار ذرات البروتين CA والذرات الثقيلة (NH1 ، NH2 ، OH ، NZ ، NE2 ، ND2) من بقايا Y119 ، K122 ، K125 ، R131 ، Y133 ، Q146 ، K144 ، R135 ، W116 ، R117 ، Y134 ، K118 ، Q121 التي يمكن أن تشكل روابط هيدروجينية (HBs) مع نيوكليوتيد الحمض النووي ، والتي تقترن مع ذرات O1P O2P و N6 من نيوكليوتيد الحمض النووي (A14-20 ، T19-23). يمكن للأحماض الأمينية المختارة إما أن تشكل HBs مستقرة أو جسور ملحية مع الحمض النووي.
    3. انسخ فهرس الذرة المحدد أعلاه من ملف index.ndx إلى ملف نصي جديد (index.dat). احصل على معلومات الزوج بين هذه الذرات بواسطة برنامج python النصي من الملف التكميلي 1 generate_atom_indices.py والنوع:
      مؤشر generate_atom_indices.py python2.6.dat > مؤشرات الذرة.txt
      هذا يولد 415 زوجا من المسافة بين البروتين والحمض النووي.
    4. حساب أزواج المسافة 415 من كل مسار عن طريق كتابة الأمر التالي في إطار الأمر MSMbuilder:
      MSMB AtomPairsFeaturizer -out pair_features --pair_indices AtomIndices.txt --أعلى المراجع.pdb --trjs "مسارات/*.xtc" --تحويل pair_features --خطوة 5
    5. قم بإجراء tICA لتقليل بعد البيانات على أول 2 مكون مستقل عن الوقت (tICs) أو متجهات عن طريق كتابة:
      MSMB tICA -i .. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --غاما 0.05 -t tica_results.h5
      ملاحظة: tICA هي طريقة لتقليل الأبعاد تحسب القيمة الذاتية لمصفوفة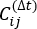 figure-protocol-5652 الارتباط المتخلفة زمنيا لتحديد أبطأ درجات الاسترخاء لحرية نظام المحاكاة بواسطة المعادلة: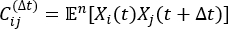
      figure-protocol-5811
      حيث X i(t) هي قيمة إحداثيات التفاعل i-th في الوقت t ، و X j (t + Δ t) هي قيمةإحداثيات تفاعل j-th في الوقت t + Δ t.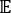 figure-protocol-6090 هي القيمة المتوقعة لناتج مسارات المحاكاة الكلية Xi(t) وX j(t + Δ t). تتوافق الاتجاهات على طول أبطأ درجات الاسترخاء من الحرية مع أكبر القيم الذاتية لمصفوفة 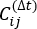figure-protocol-6379الارتباط المتخلفة زمنيا أعلاه . هنا ، يبدو أن 2 tICs هي مجموعة دنيا للتمييز بين ثلاث حالات كلية على بناء MSM الخاص بنا (يتم تناوله لاحقا). يمكن للمرء أيضا حساب درجة حاصل رايلي المعمم (GMRQ)49 ، على سبيل المثال ، لاستكشاف مجموعة مثالية من المكونات التي سيتم استخدامها.
    6. استخدم الأمر في MSMbuilder لتجميع مجموعات البيانات المسقطة في 100 مجموعة بواسطة طريقة K-center43,44 (انظر الشكل 1B):
      MSMB KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 100.
      حدد الهيكل المركزي لكل مجموعة كهيكل أولي للجولة 2الثانية من محاكاة MD. الحفاظ على معلومات المحاكاة الخاصة بهياكل 100 المحاكاة، بما في ذلك المواقع ودرجات الحرارة والضغوط وما إلى ذلك، باستثناء السرعات.
      ملاحظة: بعد الجولة الأولى من 25 عملية محاكاة، تم تقليل ذاكرة المسار الأولي، لذلك قمنا بإنشاء المزيد من المجموعات، على سبيل المثال، 100 مجموعة، في الجولة الثانية، لتوسيع العينات المطابقة بشكل كبير.
  4. إجراء الجولةالثانية 2 محاكاة MD واسعة النطاق
    1. قم بإجراء محاكاة MD 60-ns بدءا من هذه الهياكل الأولية 100 بعد فرض سرعات أولية عشوائية على جميع الذرات. أضف السرعات الأولية العشوائية عن طريق تشغيل توليد السرعة في ملف mdp ، أي تغيير ملف md.mdp gen_vel = لا إلى gen_vel = نعم.
    2. قم بإزالة أول 10 نانو ثانية من كل محاكاة كما هو موضح في الخطوة 1.3.1 ، واجمع 2,500,000 لقطة من مسارات 100 × 50 ns بالتساوي لبناء MSM.
      ملاحظة: لاحظ أنه في بناء الحالات الكلية اللاحقة، تم العثور على عدد صغير من الحالات خارج المسار ذات عدد السكان المنخفض بشكل خاص (~ 0.2٪، في الجزء السفلي من مستوى X-Θ). يتم تصنيف هذه الحالات خارج المسار كحالة كلية واحدة عندما يتم تعيين العدد الإجمالي للحالات الكلية على أنها 3 إلى 6 (الشكل 2B). نظرا لأن هذه الحالة الكلية السكانية المنخفضة لا تشمل سوى 3 مسارات ، والتي تمت إزالتها في النهاية ، فقد تم الحصول على النتائج الموضحة في هذا البروتوكول بالفعل من مسارات 97 × 50 ns ، مع ما مجموعه 2،425،000 إطار أو لقطة.
  5. تجميع مسارات MD الجولةالثانية 2
    1. إجراء tICA لمسارات الجولة2 كما كان يحدث سابقا. اكتب في MSMbuilder:
      MSMB tICA -i .. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --غاما 0.05 -t tica_results.h5
    2. حساب المقياس الزمني الضمني للتحقق من صحة المعلمات الخاصة بوقت تأخير الارتباط Δt وأرقام الحالات الدقيقة (انظر الشكل 1C) ،
      figure-protocol-8910
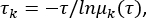
      حيث يمثل τ وقت التأخير المستخدم لبناء مصفوفة احتمال الانتقال (TPM) ؛ يمثل μk(τ) القيمة الذاتية kth ل TPM تحت وقت تأخير τ. استخدم البرنامج النصي python من الملف التكميلي 1 لهذا الثعبان BuildMSMsAsVaryLagTime.py -d .. / -و .. /trajlist_num -i 50 -m 1000 -t 10 -n 20 -s 500.
    3. قم بتغيير وقت التأخر τ وعدد الحالات الدقيقة عن طريق تغيير المعلمات المستخدمة أعلاه:
      الثعبان BuildMSMsAsVaryLagTime.py -d .. / -و .. /trajlist_num -i 50 -m 1000 -t 5 10 20 30 40 -n 20 -s 20 200 400 500 800 2000
      ملاحظة: يعتبر النظام ماركوفيان عندما تبدأ منحنيات المقياس الزمني الضمنية في التسوية مع فصل المقياس الزمني. ثم اختر Dt كوقت تأخير الارتباط و τ وقت التأخر حيث يبدأ المقياس الزمني الضمني في الاستقرار لإنشاء MSM.
    4. وفقا لذلك ، اختر عددا كبيرا نسبيا (ولكن ليس كبيرا جدا) من الحالات ، N = 500 ، ووقت تأخير ارتباط قصير نسبيا Δt = 10 ns. تم العثور على وقت التأخر ليكون τ = 10 ns لبناء MSM.
    5. صنف التكوينات إلى 500 مجموعة (انظر الشكل 1D) باستخدام الأمر:
      MSMB KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 500
  6. بناء سوق مسقط للأوراق المالية
    1. قم بتجميع 500 حالة دقيقة في 3-6 حالات كبيرة لمعرفة عدد الحالات الكلية التي تناسب بشكل أفضل وفقا لخوارزمية PCCA+50 في MSMbuilder ، باستخدام البرنامج النصي python في الملف التكميلي 1 python msm_lumping_usingPCCAplus.py. تحديد شبكة حركية مخفضة من النماذج للتغيرات التوافقية الأكثر أهمية للجزيئات الحيوية ، من خلال بناء عدد صغير من الحالات الكلية ، أي عند تجميع مئات الحالات الدقيقة حركيا كما هو موضح أدناه17,51.
    2. ارسم خريطة للتكوينات عالية الأبعاد ل X (حركة البروتين على طول محور الحمض النووي الطويل) وزاوية دوران البروتين على طول الحمض النووي لكل حالة كبيرة كما هو موضح في الخطوة 1.1.3 و 1.1.4 (على سبيل المثال ، لا توجد حالة ذات عدد سكان منخفض للغاية < 1٪ ؛ انظر الشكل 2C). ثم ابحث عن 3 حالات ماكرو تمثل النظام بشكل أفضل (الشكل 1E) . انظر الشكل 2D للحصول على لقطات لحركة البروتين على طول الحمض النووي وزاوية دوران البروتين حول الحمض النووي.
      ملاحظة: في العمل السابق الذي يولد مسار التقدم التلقائي للبروتين 10 ميكروثانية إلى الأمام ، أجرينا أيضا محاكاة MD لتوازن 5 × 4 ميكروثانية لتوسيع العينات بشكل معتدل. أظهرنا رسم خرائط للمسار الأمامي الأصلي (انظر الشكل 2A إلى اليسار) ومسارات أخذ عينات أخرى من 4-μs على المسار الأمامي أجريت سابقا (انظر الشكل 2A إلى اليمين)8. ويرد رسم خرائط للمسارات الأصلية 100 × 50 ns (انظر الشكل 2B إلى اليسار)8 والمسارات 97 × 50 ns المستخدمة في هذا العمل (انظر الشكل 2B إلى اليمين).
  7. حساب متوسط مرات المرور الأول (MFPT)
    1. قم بإجراء خمسة مسارات مونت كارلو (MC) بسعة 10 مللي ثانية استنادا إلى TPM ل 500 microstate MSM مع تعيين وقت التأخر البالغ 10 ns كخطوة زمنية ل MC. حساب MFPT52 بين كل زوج من الحالات الكبيرة (الشكل 3) بواسطة البرنامج النصي python في الملف التكميلي 1 python python mfpt_msm3.py.
    2. حساب متوسط والخطأ القياسي ل MFPT باستخدام ملف bash في الملف التكميلي 2، اكتب:
      ش mfpt_analysis.باش

2. إجراء محاكاة الحبيبات الخشنة (CG) لأخذ عينات من الديناميكيات طويلة الأمد

  1. قم بإجراء محاكاة CG باستخدام برنامج CafeMol 3.030. راجع إعدادات محاكاة CG المحددة في ملف تكوين الإدخال بامتداد .inp، بما في ذلك هياكل الإدخال ومعلمات المحاكاة وملفات الإخراج وما إلى ذلك. اكتب الأمر التالي على المحطة الطرفية لتشغيل محاكاة CG:
    كافيمول XXX.inp
  2. حدد الكتل التالية في ملف الإدخال، مع بدء كل كتلة بالتسمية < and ending with >>>>.
    1. قم بتعيين كتلة أسماء الملفات (مطلوبة) لتحديد أدلة العمل ومسار مخزن ملفات الإدخال / الإخراج. اكتب ما يلي لكتلة أسماء الملفات لعمليات المحاكاة هذه:
      أسماء الملفات <<<<
      المسار = XXXXX (مسار العمل)
      اسم الملف = wrky (أسماء ملفات الإخراج)
      OUTPUT psf pdb فيلم dcd rst
      path_pdb = XXXXX (مسار البنية الأصلية للإدخال)
      path_ini = XXXXX (مسار البنية الأولية للإدخال)
      path_natinfo = XXXXX (مسار ملف المعلومات الأصلي)
      path_para = XXXXX (مسار ملفات المعلمات)
      >>>>
      ملاحظة: نظرا لاستخدام نموذج Go53 في نمذجة CG ، أي أن البروتين سيكون متحيزا للمطابقة الأصلية ، لذلك يحتاج المرء إلى تعيين الهيكل النموذجي على أنه التشكيل الأصلي. هنا ، تم تعيين بنية بلورية الإدخال كمطابقة أصلية.
    2. قم بتعيين كتلة التحكم في المهمة (مطلوبة) لتحديد وضع تشغيل عمليات المحاكاة. اكتب الأمر التالي:
      <<<< job_cntl
      i_run_mode = 2 (= 2 محاكاة درجة الحرارة الثابتة)
      i_simulate_type = 1 (= 1 ديناميكيات لانجفين)
      i_initial_state = 2 (=2 يعني أن التكوين الأولي هو التكوين الأصلي)
      >>>>
      حدد درجة الحرارة الثابتة محاكاة ديناميكيات Langevin.
    3. قم بتعيين الوحدة وكتلة الحالة (مطلوبة) لتحديد المعلومات الخاصة بهياكل الإدخال. اكتب الأمر التالي:
      <<<< unit_and_state
      i_seq_read_style = 1 (= 1 يعني قراءة التسلسلات من ملف PDB)
      i_go_native_read_style = 1 (= 1 يعني أن البنية الأصلية من ملف PDB)
      1 بروتين بروتين.pdb (وحدة molecular_type native_structure الحالة)
      2-3 الحمض النووي الحمض النووي.pdb (وحدة &الدولة molecular_type native_structure)
      >>>>
      ملاحظة: هناك حاجة إلى ملفات بنية الإدخال الأولية (البروتين .pdb والحمض النووي .pdb هنا). تتم كتابة الهياكل بتنسيق pdb. هناك حاجة إلى ملفين pdb هنا: أحدهما هو ملف بنية البروتين الذي يحتوي على إحداثيات الذرة الثقيلة ل WRKY (الوحدة 1) ، والآخر هو إحداثيات الحمض النووي المزدوج (ds) 200-bp (الوحدة 2-3). يتم وضع البروتين في البداية على بعد 15 Å بعيدا عن الحمض النووي.
    4. اضبط كتلة دالة الطاقة (المطلوبة) المحددة في كتلة energy_function. اكتب الأمر التالي:
      <<<< energy_function
      محلي(1) L_GO
      محلي(2-3) L_DNA2
      NLOCAL(1/1) الذهاب إكس إيلي
      NLOCAL (2-3/2-3) الحمض النووي ELE
      NLOCAL (1/2-3) EXV ELE
      i_use_atom_protein = 0
      i_use_atom_dna = 0
      i_para_from_ninfo = 1
      i_triple_angle_term = 2
      >>>>
      ملاحظة: في عمليات محاكاة CG ، يكون البروتين خشنا الحبيبات بواسطة نموذج Go53 مع كل حمض أميني يمثله جسيم CG يوضع في موضع Cα الخاص به. سيكون تشكيل البروتين منحازا بعد ذلك نحو البنية الأصلية ، أو البنية البلورية هنا ، تحت إمكانات Go (الشكل 4A على اليسار). يتم وصف الحمض النووي بواسطة نموذج 3SPN.254 ، حيث يتم تمثيل كل نيوكليوتيد بواسطة 3 جسيمات CG S ، P ، N ، والتي تتوافق مع السكر والفوسفات والقاعدة النيتروجينية ، على التوالي (الشكل 4A يمين). يتم النظر في التفاعلات الكهروستاتيكية و vdW بين سلاسل مختلفة. يتم تقريب التفاعلات الكهروستاتيكية بين البروتين والحمض النووي في محاكاة CG بواسطة جهد Debye-Hückel55. تأخذ الطاقة المثيرة للاشمئزاز vdW نفس الشكل كما هو الحال في نموذج Go.
    5. قم بتعيين كتلة md_information (مطلوبة) لتحديد معلومات المحاكاة. اكتب الأمر التالي:
      <<<< md_information
      n_step_sim = 1
      n_tstep(1) = 500000000
      tstep_size = 0.1
      n_step_save = 1000
      n_step_neighbor = 100
      i_com_zeroing = 0
      i_no_trans_rot = 0
      تيمبك = 300.0
      n_seed = -1
      >>>>
      n_tstep هي خطوة المحاكاة. قم بتعيين tstep_size كطول زمني لكل خطوة MD ، كل خطوة زمنية CG Cafemol حوالي 200 fs30 ، لذلك كل خطوة MD هنا هي 200 × 0.1 fs من حيث المبدأ. قم بتحديث قائمة الجيران كل 100 خطوة MD (n_step_neighbor = 100). اضبط درجة حرارة المحاكاة على 300 K. تحكم في درجة الحرارة عن طريق استخدام خوارزمية Verlet من نوع السرعة لتحديث بنية البروتين باستخدام ترموستات Berendsen56.
      ملاحظة: n_step_sim هو رقم الحوض للإمكانات القائمة على نموذج Go ، أو الحد الأدنى المحلي لعدد منحنى الطاقة. تسمح إمكانات الأحواض المتعددة بتشكيل البروتين المنحاز إلى تكوينات مختلفة بحيث يمكن أن يتغير تشكيل البروتين من حد أدنى محلي إلى آخر. هنا يتم استخدام نموذج Go لحوض واحد فقط ، مما يعني تشكيلا متحيزا واحدا فقط (بنية بلورية) للبروتين في عمليات المحاكاة. وفي الوقت نفسه ، نظرا لعدم وجود تفاعل بين الترابط الهيدروجيني بين البروتين والحمض النووي ، وما إلى ذلك ، على غرار سياق CG ، يمكن أخذ عينات من الحركات الجزيئية بشكل أسرع ، أي > 10 مرات مقارنة بالمحاكاة الذرية.
    6. قم بتعيين الكتلة الكهروستاتيكية (مطلوبة فقط عند استخدام التفاعل الكهروستاتيكي) حيث يعتبر التفاعل الكهروستاتيكي بين سلاسل مختلفة ، لذا استخدم هذه الكتلة لتحديد معلمات التفاعل الكهروستاتيكي عن طريق كتابة:
      <<<< الكهروستاتيكي
      cutoff_ele = 10.0
      ionic_strength = 0.15
      >>>>
      اضبط طول Debye في التفاعل الكهروستاتيكي على 10 Å ، المقابلة لحالة المحلول. اضبط القوة الأيونية على 0.15 م ، كما هو الحال في الحالة الفسيولوجية.

النتائج

انزلاق مقترن بالدوران أو خطوة 1 نقطة أساس من WRKY من بناء MSM
يتم تعيين جميع تكوينات البروتين على الحمض النووي إلى الحركة الطولية X وزاوية دوران البروتين COM على طول الحمض النووي (انظر الشكل 3A). يشير الاقتران الخطي لهاتين الدرجتين إلى خطوة مقترنة بالدوران لبروتين مجال ...

Discussion

يتناول هذا العمل كيفية إجراء المحاكاة الحسابية القائمة على البنية وأخذ العينات للكشف عن عامل النسخ أو بروتين TF الذي يتحرك على طول الحمض النووي ، ليس فقط في التفاصيل الذرية للخطوة ، ولكن أيضا في الانتشار العملي ، وهو أمر ضروري لتسهيل انتشار TF في البحث عن هدف الحمض النووي. للقيام بذلك ، تم بن...

Disclosures

ليس لدى المؤلفين أي تضارب في المصالح.

Acknowledgements

تم دعم هذا العمل من قبل NSFC Grant # 11775016 و #11635002. تم دعم JY من قبل CMCF التابع لشركة UCI عبر NSF DMS 1763272 ومنحة مؤسسة Simons Foundation # 594598 وصندوق بدء التشغيل من UCI. تم دعم LTD من قبل مؤسسة العلوم الطبيعية في شنغهاي #20ZR1425400 و #21JC1403100. كما نعترف بالدعم الحسابي المقدم من مركز بكين لأبحاث العلوم الحاسوبية (CSRC).

Materials

NameCompanyCatalog NumberComments
CafeMolKyoto Universitycoarse-grained (CG) simulations
GROMACSUniversity of Groningen Royal Institute of Technology Uppsala Universitymolecular dynamics simulations software
MatlabMathWorksNumerical calculation software
MSMbuilderStanford Universitybuild MSM
VMDUNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGNmolecular visualization program

References

  1. Latchman, D. S. Transcription factors: an overview. The International Journal of Biochemistry & Cell Biology. 29 (12), 1305-1312 (1997).
  2. Berg, O. G., von Hippel, P. H. Selection of DNA binding sites by regulatory proteins. Statistical-mechanical theory and application to operators and promoters. Journal of Molecular Biology. 193 (4), 723-750 (1987).
  3. von Hippel, P. H., Berg, O. G. Facilitated target location in biological systems. The Journal of Biological Chemistry. 264 (2), 675-678 (1989).
  4. Halford, S. E., Marko, J. F. How do site-specific DNA-binding proteins find their targets. Nucleic Acids Research. 32 (10), 3040-3052 (2004).
  5. Slusky, M., Mirny, L. A. Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential. Biophysical Journal. 87 (6), 4021-4035 (2004).
  6. Bauer, M., Metzler, R. Generalized facilitated diffusion model for DNA-binding proteins with search and recognition states. Biophysical Journal. 102 (10), 2321-2330 (2012).
  7. Shvets, A. A., Kochugaeva, M. P., Kolomeisky, A. B. Mechanisms of Protein Search for Targets on DNA: Theoretical Insights. Molecules. 23 (9), 2106 (2018).
  8. Dai, L., Xu, Y., Du, Z., Su, X. D., Yu, J. Revealing atomic-scale molecular diffusion of a plant-transcription factor WRKY domain protein along DNA. Proceedings of the National Academy of Sciences of the United States of America. 118 (23), 2102621118 (2021).
  9. Chodera, J. D., Singhal, N., Pande, V. S., Dill, K. A., Swope, W. C. Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. The Journal of Chemical Physics. 126 (15), 155101 (2007).
  10. Pan, A. C., Roux, B. Building Markov state models along pathways to determine free energies and rates of transitions. The Journal of Chemical Physics. 129 (6), 064107 (2008).
  11. Bowman, G. R., Huang, X., Pande, V. S. Using generalized ensemble simulations and Markov state models to identify conformational states. Methods. 49 (2), 197-201 (2009).
  12. Prinz, J. H., et al. Markov models of molecular kinetics: Generation and validation. The Journal of chemical physics. 134 (17), 174105 (2011).
  13. Chodera, J. D., Noé, F. Markov state models of biomolecular conformational dynamics. Current Opinion in Structural Biology. 25, 135-144 (2014).
  14. Malmstrom, R. D., Lee, C. T., Van Wart, A. T., Amaro, R. E. On the Application of Molecular-Dynamics Based Markov State Models to Functional Proteins. Journal of Chemical Theory and Computation. 10 (7), 2648-2657 (2014).
  15. Husic, B. E., Pande, V. S. Markov State Models: From an Art to a Science. Journal of the American Chemical Society. 140 (7), 2386-2396 (2018).
  16. Sittel, F., Stock, G. Perspective: Identification of collective variables and metastable states of protein dynamics. The Journal of chemical physics. 149 (15), 150901 (2018).
  17. Wang, W., Cao, S., Zhu, L., Huang, X. Constructing Markov State Models to elucidate the functional conformational changes of complex biomolecules. WIREs Computational Molecular Science. 8, 1343 (2018).
  18. Peng, S., et al. Target search and recognition mechanisms of glycosylase AlkD revealed by scanning FRET-FCS and Markov state models. Proceedings of the National Academy of Sciences of the United States of America. 117 (36), 21889-21895 (2020).
  19. Tian, J., Wang, L., Da, L. T. Atomic resolution of short-range sliding dynamics of thymine DNA glycosylase along DNA minor-groove for lesion recognition. Nucleic Acids Research. 49 (3), 1278-1293 (2021).
  20. Chu, J. -. W., Izveko, S., Voth, G. The multiscale challenge for biomolecular systems: coarse-grained modeling. Molecular Simulation. 32 (3-4), 211-218 (2006).
  21. Marrink, S. J., Risselada, H. J., Yefimov, S., Tieleman, D. P., De Vries, A. H. The MARTINI force field: coarse grained model for biomolecular simulations. The Journal of Physical Chemistry B. 111 (27), 7812-7824 (2007).
  22. Givaty, O., Levy, Y. Protein sliding along DNA: dynamics and structural characterization. Journal of Molecular Biology. 385 (4), 1087-1097 (2009).
  23. Khazanov, N., Levy, Y. Sliding of p53 along DNA can be modulated by its oligomeric state and by cross-talks between its constituent domains. Journal of Molecular Biology. 408 (2), 335-355 (2011).
  24. Riniker, S., Allison, J. R., van Gunsteren, W. F. On developing coarse-grained models for biomolecular simulation: a review. Physical Chemistry Chemical Physics : PCCP. 14 (36), 12423-12430 (2012).
  25. Kmiecik, S., et al. Coarse-Grained Protein Models and Their Applications. Chemical Reviews. 116 (14), 7898-7936 (2006).
  26. Bhattacherjee, A., Krepel, D., Levy, Y. Coarse-grained models for studying protein diffusion along DNA. WIREs Computational Molecular Science. 6, 515-531 (2016).
  27. Wang, J., et al. Machine Learning of Coarse-Grained Molecular Dynamics Force Fields. ACS Central Science. 5 (5), 755-767 (2019).
  28. Joshi, S. Y., Deshmukh, S. A. A review of advancements in coarse-grained molecular dynamics simulations. Molecular Simulation. 47 (10-11), 786-803 (2021).
  29. Bigman, L. S., Greenblatt, H. M., Levy, Y. What Are the Molecular Requirements for Protein Sliding along DNA. The Journal of Physical Chemistry B. 125 (12), 3119-3131 (2021).
  30. Kenzaki, H., et al. CafeMol: A Coarse-Grained Biomolecular Simulator for Simulating Proteins at Work. Journal of Chemical Theory and Computation. 7 (6), 1979-1989 (2011).
  31. Berendsen, H. J. C., vander Spoel, D., van Drunen, R. GROMACS: a message-passing parallel molecular dynamics implementation. Computer Physics Communications. 91 (1-3), 43-56 (1995).
  32. vander Spoel, D., et al. GROMACS: fast, flexible, and free. Journal of Computational Chemistry. 26 (16), 1701-1718 (2005).
  33. Abraham, M. J., et al. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 1-2, 19-25 (2015).
  34. Harrigan, M. P., et al. MSMBuilder: Statistical Models for Biomolecular Dynamics. Biophysical journal. 112 (1), 10-15 (2017).
  35. Humphrey, W., Dalke, A., Schulten, K. VMD: visual molecular dynamics. Journal of Molecular Graphics. 14 (1), 33-38 (1996).
  36. Izrailev, S., et al. Steered Molecular Dynamics. Computational Molecular Dynamics: Challenges, Methods, Ideas. 4, 39-65 (1999).
  37. Schlitter, J., Engels, M., Krüger, P. Targeted molecular dynamics: a new approach for searching pathways of conformational transitions. Journal of Molecular Graphics. 12 (2), 84-89 (1994).
  38. Maragliano, L., Fischer, A., Vanden-Eijnden, E., Ciccotti, G. String method in collective variables: minimum free energy paths and isocommittor surfaces. The Journal of Chemical Physics. 125 (2), 24106 (2006).
  39. Weiss, D. R., Levitt, M. Can morphing methods predict intermediate structures. Journal of Molecular Biology. 385 (2), 665-674 (2009).
  40. Xu, Y. P., Xu, H., Wang, B., Su, X. D. Crystal structures of N-terminal WRKY transcription factors and DNA complexes. Protein. 11 (3), 208-213 (2020).
  41. Higham, D. J., Higham, N. J. MATLAB guide. Society for Industrial and Applied Mathematics. , (2016).
  42. Hartigan, J. A., Wong, M. A. Algorithm AS 136: A K-Means Clustering Algorithm. Journal of the Royal Statistical Society. Series C (Applied Statistics). 28 (1), 100-108 (1979).
  43. Gonzalez, T. F. Clustering to minimize the maximum intercluster distance. Theoretical Computer Science. 38, 293-306 (1985).
  44. Zhao, Y., Sheong, F. K., Sun, J., Sander, P., Huang, X. A fast parallel clustering algorithm for molecular simulation trajectories. Journal of Computational Chemistry. 34 (2), 95-104 (2013).
  45. Ivani, I., et al. Parmbsc1: a refined force field for DNA simulations. Nature Methods. 13 (1), 55-58 (2016).
  46. Naritomi, Y., Fuchigami, S. Slow dynamics of a protein backbone in molecular dynamics simulation revealed by time-structure based independent component analysis. The Journal of Chemical Physics. 139 (21), 215102 (2013).
  47. Naritomi, Y., Fuchigami, S. Slow dynamics in protein fluctuations revealed by time-structure based independent component analysis: the case of domain motions. The Journal of Chemical Physics. 134 (6), 065101 (2011).
  48. Pérez-Hernández, G., Paul, F., Giorgino, T., De Fabritiis, G., Noé, F. Identification of slow molecular order parameters for Markov model construction. The Journal of Chemical Physics. 139 (1), 015102 (2013).
  49. McGibbon, R. T., Pande, V. S. Variational cross-validation of slow dynamical modes in molecular kinetics. The Journal of Chemical Physics. 142 (12), 124105 (2015).
  50. Deuflhard, P., Weber, M. Robust Perron cluster analysis in conformation dynamics. Linear Algebra and its Applications. 398, 161-184 (2005).
  51. Silva, D. A., et al. Millisecond dynamics of RNA polymerase II translocation at atomic resolution. Proceedings of the National Academy of Sciences of the United States of America. 111 (21), 7665-7670 (2014).
  52. Swope, W. C., Pitera, J. W., Suits, F. Describing Protein Folding Kinetics by Molecular Dynamics Simulations. 1. Theory. The Journal of Physical Chemistry B. 108 (21), 6571-6581 (2004).
  53. Clementi, C., Nymeyer, H., Onuchic, J. N. Topological and energetic factors: what determines the structural details of the transition state ensemble and "en-route" intermediates for protein folding? An investigation for small globular proteins. Journal of molecular biology. 298 (5), 937-953 (2000).
  54. Hinckley, D. M., Freeman, G. S., Whitmer, J. K., De Pablo, J. J. An experimentally-informed coarse-grained 3-Site-Per-Nucleotide model of DNA: structure, thermodynamics, and dynamics of hybridization. The Journal of chemical physics. 139 (14), 144903 (2013).
  55. Debye, P., Huckel, E. The theory of the electrolyte II-The border law for electrical conductivity. Physikalische Zeitschrift. 24, 305-325 (1923).
  56. Berendsen, H. J., Postma, J. V., van Gunsteren, W. F., DiNola, A., Haak, J. R. Molecular dynamics with coupling to an external bath. The Journal of Chemical Physics. 81, 3684-3690 (1984).
  57. Bowman, G. R. Improved coarse-graining of Markov state models via explicit consideration of statistical uncertainty. The Journal of Chemical Physics. 137 (13), 134111 (2012).
  58. Jain, A., Stock, G. Identifying metastable states of folding proteins. Journal of Chemical Theory and Computation. 8 (10), 3810-3819 (2012).
  59. Röblitz, S., Weber, M. Fuzzy spectral clustering by PCCA+: application to Markov state models and data classification. Advances in Data Analysis and Classification. 7, 147-179 (2013).
  60. Mardt, A., Pasquali, L., Wu, H., Noé, F. VAMPnets for deep learning of molecular kinetics. Nature Communications. 9 (1), 5 (2018).
  61. Wang, W., Liang, T., Sheong, F. K., Fan, X., Huang, X. An efficient Bayesian kinetic lumping algorithm to identify metastable conformational states via Gibbs sampling. The Journal of Chemical Physics. 149 (7), 072337 (2018).
  62. Chen, W., Sidky, H., Ferguson, A. L. Nonlinear discovery of slow molecular modes using state-free reversible VAMPnets. The Journal of Chemical Physics. 150 (21), 214114 (2019).
  63. Gu, H., et al. RPnet: a reverse-projection-based neural network for coarse-graining metastable conformational states for protein dynamics. Physical Chemistry Chemical Physics :PCCP. 24 (3), 1462-1474 (2022).
  64. Lane, T. J., Bowman, G. R., Beauchamp, K., Voelz, V. A., Pande, V. S. Markov state model reveals folding and functional dynamics in ultra-long MD trajectories. Journal of the American Chemical Society. 133 (45), 18413-18419 (2011).
  65. Konovalov, K. A., Unarta, I. C., Cao, S., Goonetilleke, E. C., Huang, X. Markov State Models to Study the Functional Dynamics of Proteins in the Wake of Machine Learning. JACS Au. 1 (9), 1330-1341 (2021).
  66. Cao, S., Montoya-Castillo, A., Wang, W., Markland, T. E., Huang, X. On the advantages of exploiting memory in Markov state models for biomolecular dynamics. The Journal of Chemical Physics. 153 (1), 014105 (2020).
  67. Brandani, G. B., Takada, S. Chromatin remodelers couple inchworm motion with twist-defect formation to slide nucleosomal DNA. PLoS Computational Biology. 14 (11), 1006512 (2018).
  68. Tan, C., Terakawa, T., Takada, S. Dynamic Coupling among Protein Binding, Sliding, and DNA Bending Revealed by Molecular Dynamics. Journal of the American Chemical Society. 138 (27), 8512-8522 (2016).
  69. Terakawa, T., Takada, S. p53 dynamics upon response element recognition explored by molecular simulations. Scientific reports. 5, 17107 (2015).
  70. Brandani, G. B., Niina, T., Tan, C., Takada, S. DNA sliding in nucleosomes via twist defect propagation revealed by molecular simulations. Nucleic Acids Research. 46 (6), 2788-2801 (2018).
  71. Knotts, T. A., Rathore, N., Schwartz, D. C., de Pablo, J. J. A coarse grain model for DNA. The Journal of Chemical Physics. 126 (8), 084901 (2007).
  72. Freeman, G. S., Hinckley, D. M., Lequieu, J. P., Whitmer, J. K., de Pablo, J. J. Coarse-grained modeling of DNA curvature. The Journal of Chemical Physics. 141 (16), 165103 (2014).

Reprints and Permissions

Request permission to reuse the text or figures of this JoVE article

Request Permission

Explore More Articles

181

This article has been published

Video Coming Soon

JoVE Logo

Privacy

Terms of Use

Policies

Contact Us

Recommend to library

JoVE NEWSLETTERS

Research

Education

Authors

Librarians

ABOUT JoVE

Copyright © 2025 MyJoVE Corporation. All rights reserved