需要订阅 JoVE 才能查看此. 登录或开始免费试用。
Method Article
微米/纳米尺度应变分布测量从采样莫尔条纹
摘要
这里介绍了采用2像素和多像素采样方法进行微/纳米级高精度应变分布测量的采样莫尔技术。
摘要
这项工作描述了全场微/纳米尺度变形测量的采样莫尔技术的测量程序和原理。开发的技术可以通过两种方式进行:使用重建的多重莫尔法或空间相移采样莫尔法。当样本网格间距约为2像素时,产生2像素采样莫尔条纹以重建用于变形测量的乘法云纹图案。位移和应变灵敏度都是在同一广视野范围内的传统扫描波纹法的两倍。当样本网格间距大于或大于3像素时,产生多像素采样莫尔条纹,并组合空间相移技术进行全场变形测量。应变测量精度得到显着提高,并且易于实现自动批量测量。两种方法都可以像传统的莫尔技术一样,测量来自单点格栅图像的二维(2D)应变分布,而不旋转样品或扫描线。作为示例,在三点弯曲试验中测量了二维位移和应变分布,包括两个碳纤维增强塑料样品的剪切应变。所提出的技术预计将在各种材料的机械性能,裂纹发生和残余应力的非破坏性定量评估中发挥重要作用。
引言
微/纳米尺度变形测量对于评估先进材料的机械性能,不稳定行为,残余应力和裂纹发生至关重要。由于光学技术是非接触的,全场的和非破坏性的,所以已经开发了用于近几十年的变形测量的各种光学方法。近年来,微纳米尺度变形测量技术主要包括莫尔方法1,2,3,4 ,几何相位分析(GPA) 5,6 ,傅里叶变换(FT),数字图像相关(DIC)和电子散斑图案干涉测量(ESPI)。在这些技术中,由于存在多个频率,所以GPA和FT不太适用于复杂的变形测量。 DIC方法是sim因为变形载体是随机斑点,而是无噪声。最后,ESPI对振动非常敏感。
在微/纳米级莫尔方法中,目前最常用的方法是显微镜扫描莫尔法,例如电子扫描莫尔7,8,9 ,激光扫描莫尔10,11和原子力显微镜(AFM)莫尔12 ,以及一些基于显微镜的莫尔方法,例如数字/重叠莫尔13,14,15方法和乘法/分数莫尔法16,17 。扫描莫尔法具有广泛的视野,高分辨率等诸多优点并且对随机噪声不敏感。然而,传统的扫描莫尔法对于2D应变测量是不方便的,因为需要将样品台或扫描方向旋转90°并扫描两次以在两个方向18上产生莫尔条纹。旋转和双重扫描过程引入旋转误差并花费很长时间,严重影响2D应变的测量精度,特别是对于剪切应变。虽然时间相移技术19,20可以提高变形测量精度,但是它需要时间和特殊的相移装置不适于动态测试。
采样莫尔法21,22在位移测量中具有高精度,并且现在主要用于当汽车p屁股。为了将采样莫尔法扩展到微尺度/纳米尺度的2D应变测量,从2像素采样莫尔条纹开始,新开发了一种重新构成的多重波纹法,其中测量是灵敏度的两倍,保持扫描波纹法。此外,空间相移采样莫尔法也是从多像素采样莫尔条纹开发的,允许进行高精度应变测量。该协议将介绍详细的应变测量程序,并有望帮助研究人员和工程师学习如何测量变形,改进材料和产品的制造过程。
研究方案
1.样品上的微/纳米级网格的确认
- 样品加工
- 将样品切割成在显微镜下使用的特定加载装置( 例如, 1×5×30mm 3 )所需的尺寸,使得观察到的表面比感兴趣区域大1.5倍。
- 对待观察的样品表面进行抛光( 例如, 1 x 30 mm 2 ),连续在自动抛光机上使用粗细砂纸( 例如,使用SiC箔#320 3分钟,然后在800 rpm下#800进行1分钟和30 N)。每次抛光步骤后,用水清洗样品。
- 抛光相同的样品表面,依次在自动抛光机上使用粗精细抛光溶液( 例如,使用DP-Spray P 15μm,5 min,P 1μm,8 min,P 0.25μm,150 rpm,10 min; 30 N)。每次抛光后用水清洗样品g步。
- 如果标本上没有定期图案,则制作微/纳米尺度网格
注意:如果样品表面上的微/纳米级上存在天然周期性图案,则可以省略此步骤。从以下选择栅极制造方法:紫外线(UV)或加热纳米压印光刻(NIL) 26 ,电子束光刻(EBL) 2和聚焦离子束(FIB)铣削6 。
注意:这里介绍了网格制作过程,以UV NIL为例。- 使用移液管在样品表面上滴2 mL紫外线抗蚀剂。
- 使用旋转涂布机以1500rpm将样品表面上的抗蚀剂涂覆60秒。
- 在0.2MPa的压力下将纳米压印模压制成抗蚀剂层。将抗蚀剂用波长为375nm的UV曝光30秒。
- 将纳米压印模具与样品表面分开。
- 使用显微镜观察样本上的网格
- 使用离子涂布机( 例如, 3Pa的涂覆30秒,溅射电流为30mA)在网格表面上涂覆厚度为3-10nm的铂或金层。
- 将样品置于激光扫描显微镜(LSM) 23下 。
注意:也可以使用其他显微镜,例如透射电子显微镜(TEM) 5 ,原子力显微镜(AFM) 12或扫描电子显微镜(SEM) 7 。 - 通过点击显微镜图像记录软件中的"捕获"和"文件|导出|图像文件",使用显微镜调整焦点并保存一个网格图像。
- 从网格图像计算样本的网格间距(nm或μm)
- 计算超过10克的平均值在网格图像的中央区域的id间距,以避免扫描或镜头失真的潜在影响。
注意:样品上的网格可以在室温下保存几天。
- 计算超过10克的平均值在网格图像的中央区域的id间距,以避免扫描或镜头失真的潜在影响。
2.在加载测试中获取网格图像
- 显微镜下加载试验的准备
- 在显微镜下将样品固定到加载装置,例如拉伸,压缩,加热或电加载装置。
注意:如果栅格间距小于20 nm,应使用TEM或AFM。如果网格间距为20nm〜10μm,则可以使用SEM。如果网格间距大于400nm,则可以使用LSM。 - 根据具体要求设置负载速度( 例如, 0.01 mm / s)和负载或位移增量步长( 例如, 0.5 N /步或0.024 mm /步)。将负载和位移预设为零。
- 使网格冲浪ace在观察平面。通过移动或旋转显微镜的样品台,在低倍率下选择感兴趣的区域。
- 通过使图像中的网格间距大于1.8×1像素大小来选择适当的放大倍率。
注意:通常,最好使图像中的网格间距大于2像素。一个网格间距对应的像素越多,变形测量的精度越高,但测量的视场越小。
- 在显微镜下将样品固定到加载装置,例如拉伸,压缩,加热或电加载装置。
- 加载测试中的网格图像集合
- 通过点击显微镜图像记录软件中的"捕获"和"文件|导出|图像文件"来保存加载区域的网格图像。
- 开始使用加载装置的操作软件,通过施加第一加载步骤( 例如, 0.5N或0.024mm)将样品原位载入显微镜。
- 录音在显微镜的图像记录软件中单击"捕获"和"文件|导出|图像文件" ,在第一次加载步骤后( 例如, 0.5 N或0.024 mm)处理感兴趣区域的网格图像。确保显微镜的放大倍数和工作距离保持不变。
- 通过使用装载装置执行每个加载步骤继续加载样品。在每个加载步骤之后记录网格图像,直到样品断裂或直到达到某个值( 例如,负载19次,并以0.5的间隔以1 N,1.5 N,2.0 N,...,10 N记录19个网格图像N;或0.048mm,0.072mm,0.096mm,...,0.48mm,间隔为0.024mm)。确保显微镜的放大倍数和工作距离保持不变。
注意:网格图像可以任意长时间保存。
Def。之前和之后的采样莫尔条纹的生成ormation
- 网格图像中网格间距(像素)的估计
- 通过在图像处理软件( 例如, Microsoft Paint)中测量两个相邻网格点的中心之间的距离,在加载前估算网格图像中的网格间距(单位:像素)。
- 以最大负载估计网格图像中的网格间距。
- 取样间距(像素)的确定
- 当变形前后的网格间距为1.8至2.5像素时,转到步骤3.2.2。当变形前后的网格间距在2.4和3.6像素之间时跳到步骤3.2.3。当变形前后的网格间距大于3.2像素时跳到步骤3.2.4。
- 将采样间距设置为T = 2像素。跳到步骤3.3。
- 将采样间距设置为T = 3像素。跳到步骤3.3。
- 将采样间距T设置为正整数在0.75x和1.25x之间变形前后的网格间距,由丰富的模拟结果22确定 。
注意:如果有2个正整数满足步骤3.2.1和3.2.4中的要求,最好选择较大的整数作为采样间距。如果有3个或更多的正整数满足要求,最好选择中间整数,只要它比采样间距稍大一点。
- 变形前产生采样莫尔条纹
- 变形前打开网格图像。假设x方向水平向右, y方向垂直向下,坐标(0,0)位于左上角,计算x方向的图像宽度W和y方向上的图像高度H 。
注意: y方向也可以定义为垂直向上 - 转到步骤3.3.3,在y方向产生莫尔条纹。跳到步骤3.3.7在x方向产生莫尔条纹。
- 使用低通滤波器(LPF)将网格图像处理为光栅图像。例如,使用FT算法来抑制光栅,其主方向为x ,其中主方向被定义为垂直于光栅线的方向。将过滤器尺寸设置为接近网格间距。
- 通过仅从几个水平线中提取灰度值,从y = k个像素( k = 0)( 图1 )的采样间距T (T≥2)的间距( 即仅保持灰色) y = k像素, y = k + T像素,..., y = k + iT像素的采样线中的值,其中i是po坐标整数)。使最后一个采样线的坐标k + iT小于图像高度H。
- 通过用水平采样线执行图像的全场强度插值(线性或B样条),在y方向上生成采样波纹图案。
- 通过在1像素的增量步长处改变k来重复步骤3.3.4和3.3.5 T -1次,从而在y方向上生成其他T -1采样莫尔图案( 即,将变薄的起始点移动到y = k像素; k = 1,..., T -1)。
- 在步骤3.3.3-3.3.6中使用与步骤3.3.3-3.3.6相同的步骤,通过在步骤3.3.3中将x改变为y来在x方向上生成T阶梯空间相移采样莫尔图案,将图像高度H更改为图像宽度W ,并在步骤3.3中将y更改为x 。4-3.3.6。
注意: x方向上的采样间距可能与y方向不同。
- 变形前打开网格图像。假设x方向水平向右, y方向垂直向下,坐标(0,0)位于左上角,计算x方向的图像宽度W和y方向上的图像高度H 。
- 变形后产生采样莫尔条纹
- 在不同的负载下打开所有网格图像。假设网格图像的数量为N。
- 通过重复步骤3.3.3-3.3.6 N次,在y方向生成N组T阶空间相移莫尔条纹。
- 通过重复步骤3.3.7 N次,在x方向生成N组T阶梯空间相移莫尔条纹。
加载试验中样品的变形测量
- 变形前后莫尔条纹强度的确定
- 在t变形前提取T形波纹条纹的强度他的方向在步骤3.3.5和3.3.6;在步骤3.3.7中确定x方向上的莫尔强度。使用下列公式描述j ( j = x , y )方向变形前的T阶(T≥2)莫尔强度:
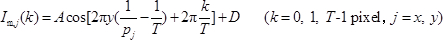 (1)
(1)
其中p j是在j ( j = x , y )方向变形之前的网格间距, A是调制幅度, D包括背景和较高频率强度。 - 在步骤3.4.2中,在y方向上提取T形台阶莫尔条纹的强度,并在步骤3.4.3中确定x方向上的莫尔强度。描述变形后的T级 (T≥2)莫尔强度通过将I m, j ( k ), p j , A和D改变为I 'm,j ( k ), p ' ,使用与上述相同的等式(等式1),在j ( j = x , y ) j , A '和D ',其中上标单引号意味着变形后。
注意:如果采样间距为T≥3像素,请忽略此步骤,然后跳至步骤4.3。
- 在t变形前提取T形波纹条纹的强度他的方向在步骤3.3.5和3.3.6;在步骤3.3.7中确定x方向上的莫尔强度。使用下列公式描述j ( j = x , y )方向变形前的T阶(T≥2)莫尔强度:
- 从变形前的两步采样莫尔强度( 图1a )之间的乘积干涉重建多重莫尔条纹,使用以下等式23
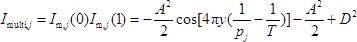 (2)
(2)
我在哪里, j代表强度of在变形前在j ( j = x , y )方向上重构的多重莫尔条纹。 - 使用条纹定心技术24在变形前处理重建的多重莫尔条纹。为连续的整数和半整数f j = [1,1.5,2,2.5,...]分配给重建的叠加莫尔条纹中心线的边界。
注意:如果乘法莫尔条纹太密集,则可以首先确定两步采样莫尔条纹的边界( 即,f j ( 0)= [1,0,2,0,3,0,...]和f j (1)= [0,1.5,0,2.5,0,3.5,...])。乘法莫尔条纹的边缘顺序将为f j = f j (0)+ f j (1)= [1,1.5,2,2.5,3,3.5,...]。刚体位移不会影响应变结果。 - 使用以下等式23测量变形前样品相对于采样间距的相对应变
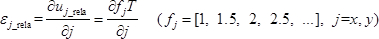 (3)
(3) 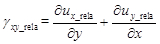 (4)
(4)
其中u j _rela和εj _rela分别表示在j ( j = x , y )方向变形之前样品的相对位移和相对应变,γxy _rela表示变形前的相对剪切应变。 - 重复步骤4.2.1-4.2.3确定样品在x和y方向变形后的相对应变N次,改变I multi, j , I m, j (0), I m, j , j , I ',(1), p ( j ),( j ), j , j , m, j (0), I 'm, j (1), p'j , A ', D ', u'j _rela (j = x,y), ε'j _rela和γ'xy _上标单引号表示变形后。
- 确定j ( j = x , y )方向上的实际正应变εj,其是网格间距和剪切应变的相对变化,γxy,这是绝对值e由变形前后相对应变载荷引起的试样网格角变化20 。
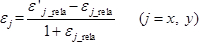 (5)
(5) 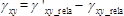 (6)
(6)
- 从变形前的两步采样莫尔强度( 图1a )之间的乘积干涉重建多重莫尔条纹,使用以下等式23
- 采样间距为T≥3像素时的变形测量
- 使用空间相移技术计算k = 0时变形前的j ( j = x , y )方向上的采样莫尔条纹的相位( 图1b ) 21
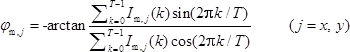 (7)
(7) - 当k = 0时,通过代替φm获得变形后的j ( j = x , y )方向上的采样莫尔条纹的相位, j和I m, j ( k )在等式(7)中分别为φ'm , j和I 'm, j ( k ),其中上标单引号表示变形后。对N个负载重复N次。
注意:如果在步骤4.3.1和4.3.2中的相位分布中存在太多的随机噪声,则可以使用sin / cos滤波器25来平滑相位。 - 确定变形前后的j ( j = x , y )方向上的采样莫尔条纹的相位差( 即 Δφm , j =φ'm , j - φm , j )。
- 测量位移u j ,正应变εj的分布 j( j = x , y )方向,由载荷引起的试样的剪切应变γxy。使用以下等式6,21
 (8)
(8) 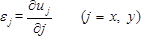 (9)
(9) 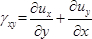 (10)
(10)
注意:如果应变分布中的噪声太大,可以使用平均滤光片,滤光片尺寸小于2个网格间距。
- 使用空间相移技术计算k = 0时变形前的j ( j = x , y )方向上的采样莫尔条纹的相位( 图1b ) 21
- 结果存储
- 保存莫尔条纹,相位(采样间距为T≥3像素)的数据,图像形式的位移和应变,如.tif或.bmp文件和文本,如.txt或.csv文件。
结果
根据莫尔形成原理23和测量过程( 图1 )测量两种碳纤维增强塑料(CFRP)样品(#1和#2)的二维位移和应变分布。 CFRP样品由10-11μm直径的K13D碳纤维和环氧树脂制成。使用来自两步采样莫尔条纹的重建的叠加莫尔法确定CFRP#1的变形,并且使用来自三步采样莫尔条纹的空间相移采样莫尔法测量CFRP#2的变形。
讨论
在所描述的技术中,如果样品上没有周期性图案,则一个具有挑战性的步骤是微/纳米尺度网格或光栅(缩写为格栅)制造26 。变形前网格间距应均匀,因为它是变形测量的重要参数。如果材料是金属,金属合金或陶瓷,UV或加热纳米压印光刻(NIL) 27 ,电子束光刻(EBL) 2 ,聚焦离子束(FIB)铣削6或网格重复法
披露声明
作者没有什么可以披露的。
致谢
这项工作由JSPS KAKENHI,授权号JP16K17988和JP16K05996以及由内阁办公室经营的跨部门战略创新促进计划D66,结构材料创新测量与分析(SIP-IMASM)支持。作者也对Drs感激不尽。 NISSISISISISISHI和Kimiyoshi Naito的CFRP材料。
材料
| Name | Company | Catalog Number | Comments |
| Automatic Polishing Machine | Marumoto Struers K.K. | LaboPol-30, Labor Force-100 | |
| Carbon Fiber Reinforced Plastic | Mitsubishi Plastics, Inc. | HYEJ16M95DHX1 | |
| Computer | DELL Japan | VOSTRO | Can be replaced with another computer with C++ programming language |
| Image Recording Software | Lasertec Corporation | LMEYE7 | Installed in a laser scanning microscope |
| Ion Coater | Japan Electron Optics Laboratory Ltd. | JEC3000F | |
| Laser Scanning Microscope | Lasertec Corporation | OPTELICS HYBRID | |
| Nanoimprint Device | Japan Laser Corporation | EUN-4200 | Can be replaced with a electron beam lithography device or a focused ion beam milling device |
| Nanoimprint Mold | SCIVAX Corporation | 3.0μm pitch | Customized |
| Nanoimprint Resist | Toyo Gosei Co., Ltd | PAK01 | |
| Polishing Solution | Marumoto Struers K.K. | DP-Spray P 15μm, 1μm, 0.25μm | Use from coarse to fine |
| Pipet | AS ONE Corporation | 10mL | |
| Sand Paper | Marumoto Struers K.K. | SiC Foil #320, #800 | Use from coarse to fine |
| Spin Coater | MIKASA Corporation | MS-A100 |
参考文献
- Weller, R., Shepard, B. Displacement measurement by mechanical interferometry. Proc. Soc. Exp. Stress Anal. 6 (1), 35-38 (1948).
- Kishimoto, S., Egashira, M., Shinya, N. Microcreep deformation measurements by a moiré method using electron beam lithography and electron beam scan. Opt. Eng. 32 (3), 522-526 (1993).
- Ifju, P., Han, B. Recent applications of moiré interferometry. Exp. Mech. 50 (8), 1129-1147 (2010).
- Zhang, H., Wu, C., Liu, Z., Xie, H. A curved surface micro-moiré method and its application in evaluating curved surface residual stress. Meas. Sci. Technol. 25 (9), 095002 (2014).
- Zhang, H., Liu, Z., Wen, H., Xie, H., Liu, C. Subset geometric phase analysis method for deformation evaluation of HRTEM images. Ultramicroscopy. 171, 34-42 (2016).
- Wang, Q., Kishimoto, S., Xie, H., Liu, Z., Lou, X. In situ high temperature creep deformation of micro-structure with metal film wire on flexible membrane using geometric phase analysis. Microelectron. Reliab. 53 (4), 652-657 (2013).
- Wang, Q., Kishimoto, S. Simultaneous analysis of residual stress and stress intensity factor in a resist after UV-nanoimprint lithography based on electron moiré fringes. J. Micromech. Microeng. 22 (10), 105021 (2012).
- Kishimoto, S., Wang, Q., Xie, H., Zhao, Y. Study of the surface structure of butterfly wings using the scanning electron microscopic moiré method. Appl. Opt. 46 (28), 7026-7034 (2007).
- Li, C., Liu, Z., Xie, H., Wu, D. Novel 3D SEM Moiré method for micro height measurement. Opt. Express. 21 (13), 15734-15746 (2013).
- Xie, H., Wang, Q., Kishimoto, S., Dai, F. Characterization of planar periodic structure using inverse laser scanning confocal microscopy moiré method and its application in the structure of butterfly wing. J. Appl. Phys. 101 (10), 103511 (2007).
- Tang, M., Xie, H., Wang, Q., Zhu, J. Phase-shifting laser scanning confocal microscopy moiré method and its applications. Meas. Sci. Technol. 21 (5), 055110 (2010).
- Xie, H., Kishimoto, S., Asundi, A., Boay, C. G., Shinya, N., Yu, J., Ngoi, B. K. In-plane deformation measurement using the atomic force microscope moiré method. Nanotechnology. 11 (1), 24 (2000).
- Xie, H., Liu, Z., Fang, D., Dai, F., Gao, H., Zhao, Y. A study on the digital nano-moiré method and its phase shifting technique. Meas. Sci. Technol. 15 (9), 1716 (2004).
- Wang, Q., Kishimoto, S., Yamauchi, Y. Three-directional structural characterization of hexagonal packed nanoparticles by hexagonal digital moiré method. Opt. Lett. 37 (4), 548-550 (2012).
- Liu, Z., Lou, X., Gao, J. Deformation analysis of MEMS structures by modified digital moiré methods. Opt. Lasers Eng. 48 (11), 1067-1075 (2010).
- Li, Y., Xie, H., Chen, P., Zhang, Q. Theoretical analysis of moiré fringe multiplication under a scanning electron microscope. Meas. Sci. Technol. 22 (2), 025301 (2010).
- Patorski, K., Wielgus, M., Ekielski, M., Kaźmierczak, P. AFM nanomoiré technique with phase multiplication. Meas. Sci. Technol. 24 (3), 035402 (2013).
- Wang, Q., Ri, S., Takashita, Y., Ogihara, S., Yoshida, S. Chapter 33: Full-field measurements of principal strains and orientations using moiré fringes. Advancement of Optical Methods in Experimental Mechanics. 3, 251-259 (2017).
- Wang, Z., Han, B. Advanced iterative algorithm for phase extraction of randomly phase-shifted interferograms. Opt. Lett. 29 (14), 1671-1673 (2004).
- Wang, Q., Xie, H., Hu, Z., Zhang, J., Sun, J., Liu, G. Residual thermo-creep deformation of copper interconnects by phase-shifting SEM moiré method. Appl. Mech. Mater. 83, 185-190 (2011).
- Ri, S., Fujigaki, M., Morimoto, Y. Sampling moiré method for accurate small deformation distribution measurement. Exp. Mech. 50 (4), 501-508 (2010).
- Ri, S., Muramatsu, T. Theoretical error analysis of the sampling moiré method and phase compensation methodology for single-shot phase analysis. Appl. Opt. 51 (16), 3214-3223 (2012).
- Wang, Q., Ri, S., Tsuda, H. Digital sampling Moiré as a substitute for microscope scanning Moiré for high-sensitivity and full-field deformation measurement at micron/nano scales. Appl. Opt. 55 (25), 6858-6865 (2016).
- Dai, F., Wang, Z. Automatic fringe patterns analysis using digital processing tehniques: I fringe center method. Acta Photonica Sinica. 28, 700-706 (1999).
- Gutmann, B., Weber, H. Phase-shifter calibration and error detection in phase-shifting applications: a new method. Appl. Opt. 37 (32), 7624-7631 (1998).
- Wang, Q., Kishimoto, S., Tanaka, Y., Kagawa, Y. Micro/submicro grating fabrication on metals for deformation measurement based on ultraviolet nanoimprint lithography. Opt. Lasers Eng. 51 (7), 944-948 (2013).
- Min-Jin, T., Hui-Min, X., Yan-Jie, L., Xiao-Jun, L., Dan, W. A new grating fabrication technique on metal films using UV-nanoimprint lithography. Chin. Phys. Lett. 29 (9), 098101 (2012).
转载和许可
请求许可使用此 JoVE 文章的文本或图形
请求许可探索更多文章
This article has been published
Video Coming Soon
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。