需要订阅 JoVE 才能查看此. 登录或开始免费试用。
Method Article
软材料大振幅振荡剪切响应的研究
摘要
我们提出了一个详细的协议, 概述了如何执行非线性振荡剪切流变学的软材料, 以及如何运行 SPP-LAOS 分析, 以了解作为一系列物理过程的反应。
摘要
我们研究了在水中的二甲基亚硫酸盐 (DMSO) 和黄原胶中的大振幅振荡剪切 (LAOS) 过程中表现出的物理过程序列--这两种浓缩聚合物溶液用作食品中的粘附剂,提高采收率和土壤修复。了解软材料的非线性流变行为, 对于许多消费品的设计和控制制造都很重要。研究表明, 如何将这些聚合物溶液对 LAOS 的响应从线性粘弹性向粘塑性变形的清晰过渡解释为在一段时间内再次回归。利用基于 matlab 的免费软件,通过物理过程 (spp) 技术的完全定量序列对 laos 结果进行分析。提出了用商业流变仪进行 LAOS 测量、用免费软件分析非线性应力响应以及解释 LAOS 下物理过程的详细协议。进一步表明, 在 SPP 框架内, LAOS 响应包含有关线性粘弹性、瞬态流动曲线和导致非线性开始的临界应变的信息。
引言
浓缩聚合物溶液主要用于各种工业应用, 主要是为了增加粘度, 包括食品1和其他消费品2、增强采收率3和土壤修复4。在它们的加工和使用过程中, 它们必然会在一系列时间尺度上受到大的变形。在这样的过程中, 它们表现出丰富而复杂的非线性流变行为, 这取决于流动或变形条件1。了解这些复杂的非线性流变行为对于成功控制过程、设计卓越产品和最大限度地提高能源效率至关重要。除了工业重要性外, 对了解远离平衡的聚合物材料的流变行为也有很大的学术兴趣。
由于应变和应变速率5的正交应用, 以及通过调整振幅和频率。小振幅振荡剪切应变的应力响应, 小到不干扰材料内部结构, 可以在应变相和应变相分解成分量。各组分在应变和应变速率的相位中的系数统称为动态模量6、7, 单独称为存储模量 和损耗模量.
和损耗模量. 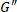 动态模量导致清晰的弹性和粘性解释。然而, 基于这些动态模量的解释仅适用于小的应变振幅, 其中对正弦激励的应力响应也是正弦的。这种状态通常被称为小振幅振荡剪切 (SAOS), 或线性粘弹性状态。随着施加变形的增大, 材料微观结构发生了变化, 这反映在非正弦瞬态应力响应的复杂性上。在这种流变非线性的状态下, 动态模量对响应的描述很差, 这种系统更密切地模仿了工业加工和消费者的使用条件。因此, 需要另一种方法来了解浓缩软材料的行为如何超出平衡。
动态模量导致清晰的弹性和粘性解释。然而, 基于这些动态模量的解释仅适用于小的应变振幅, 其中对正弦激励的应力响应也是正弦的。这种状态通常被称为小振幅振荡剪切 (SAOS), 或线性粘弹性状态。随着施加变形的增大, 材料微观结构发生了变化, 这反映在非正弦瞬态应力响应的复杂性上。在这种流变非线性的状态下, 动态模量对响应的描述很差, 这种系统更密切地模仿了工业加工和消费者的使用条件。因此, 需要另一种方法来了解浓缩软材料的行为如何超出平衡。
最近的一些研究9、10、11、12、13、14、15、16表明, 材料通过在中振幅振荡剪切 (maos)15、17和大振幅振荡剪切 (laos) 制度中, 较大的变形所引起的不同的循环内结构和动力变化。循环内结构和动力学变化有不同的表现形式, 如微观结构断裂、结构各向异性、局部重排、改造和扩散率变化。非线性状态中的这些周期内物理变化导致了复杂的非线性应力响应, 不能简单地用动态模量来解释。作为替代方法, 提出了几种解释非线性应力响应的方法。常见的例子有傅立叶变换流变学 (ft 流变学)18, 功率级数扩展11, 切比雪夫描述19, 和物理过程序列 (spp)5,8, 13、14、20分析。尽管所有这些技术在数学上都被证明是鲁棒性的, 但对于这些技术中的任何一种是否能够为非线性振荡应力响应提供清晰合理的物理解释, 这仍然是一个没有答案的问题。对与结构和动态措施相关的流变数据提供简明的解释仍然是一个突出的挑战。
在最近的一项研究中, 通过 SPP 方案分析了软玻璃流变学 (sgr) 模型8和胶体恒星聚合物7制成的软玻璃在振荡剪切下的非线性应力响应。用 SPP 模量分别量化了非线性应力响应中固有的弹性和粘性的时间变化. 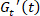
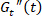 此外, 瞬态模量所表示的流变性转变与介观元素分布所代表的微观结构变化准确地相关。在 SGR 模型8的研究中, 可以清楚地表明, 通过spp 方案进行的流变解释准确地反映了软玻璃线性和非线性条件下所有振荡剪切条件下的物理变化。这种为软玻璃非线性响应提供精确物理解释的独特能力, 使 SPP 方法成为研究聚合物溶液和其他软材料不平衡动力学的研究人员的一个有吸引力的方法。
此外, 瞬态模量所表示的流变性转变与介观元素分布所代表的微观结构变化准确地相关。在 SGR 模型8的研究中, 可以清楚地表明, 通过spp 方案进行的流变解释准确地反映了软玻璃线性和非线性条件下所有振荡剪切条件下的物理变化。这种为软玻璃非线性响应提供精确物理解释的独特能力, 使 SPP 方法成为研究聚合物溶液和其他软材料不平衡动力学的研究人员的一个有吸引力的方法。
Spp 方案是围绕着将流变行为视为发生在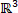 由应变 (
由应变 (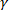 )、应变率 (
)、应变率 (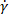 ) 和应力 (
) 和应力 ( )5组成的三维空间中构建的。从数学意义上说, 应力响应被视为应变和应变速率的多变量函数 (
)5组成的三维空间中构建的。从数学意义上说, 应力响应被视为应变和应变速率的多变量函数 (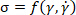 )。由于流变行为被认为是一个轨迹 (
)。由于流变行为被认为是一个轨迹 ( 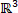 或一个多变量函数), 因此需要一个讨论轨迹特性的工具。在 SPP 方法中, 瞬态模
或一个多变量函数), 因此需要一个讨论轨迹特性的工具。在 SPP 方法中, 瞬态模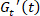 量和
量和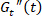 这样的作用。瞬
这样的作用。瞬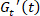 态弹性模量和粘性模
态弹性模量和粘性模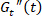 量被定义为应力相对于应变 (
量被定义为应力相对于应变 (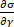 ) 和应变率 (
) 和应变率 (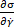 ) 的偏导数。在微分弹性和粘性模量的物理定义下, 瞬态模量分别量化了应变和应变速率对应力响应的瞬时影响, 而其他分析方法不能提供任何弹性和粘性的信息。
) 的偏导数。在微分弹性和粘性模量的物理定义下, 瞬态模量分别量化了应变和应变速率对应力响应的瞬时影响, 而其他分析方法不能提供任何弹性和粘性的信息。
SPP 方法丰富了振荡剪切试验的解释。通过 SPP 分析, saos 中浓缩聚合物溶液的复杂非线性流变行为与 SAOS 中的线性流变行为直接相关。在本工作中, 我们展示了应变极值附近的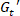 最大瞬态弹性模量 (最大) 如何与线性状态 (saos) 中的存储模量相对应。此外, 我们还展示了 LAOS 周期中的
最大瞬态弹性模量 (最大) 如何与线性状态 (saos) 中的存储模量相对应。此外, 我们还展示了 LAOS 周期中的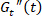 瞬态粘性模量 () 是如何跟踪稳态流动曲线的。除了提供浓缩聚合物溶液在 LAOS 下经历的复杂工艺序列的详细信息外, SPP 方案还提供了有关材料中可回收应变的信息。这些信息无法通过其他方法获得, 它是衡量一旦应力消除, 材料会退缩多少的有用指标。这种行为会影响3D 打印应用的集中解决方案的打印性能, 以及丝网印刷、纤维形成和流量停止。最近的一些研究5、8、13清楚地表明, 可回收应变不一定与 laos 实验中施加的应变相同。例如, LAOS13下的软胶体玻璃研究发现, 当总应变明显较大时, 可回收应变仅为 5% (420%)。是强加的。其他研究16,21,22, 23,24使用保持架模量21也得出结论, 线性弹性可以在 laos 下观察到在点关闭对应变最大值, 这意味着材料在这些瞬间经历了相对较小的变形。SPP 方案是理解 LAOS 的唯一框架, laos 解释了应变平衡的变化, 导致可回收应变和总应变之间的差异。
瞬态粘性模量 () 是如何跟踪稳态流动曲线的。除了提供浓缩聚合物溶液在 LAOS 下经历的复杂工艺序列的详细信息外, SPP 方案还提供了有关材料中可回收应变的信息。这些信息无法通过其他方法获得, 它是衡量一旦应力消除, 材料会退缩多少的有用指标。这种行为会影响3D 打印应用的集中解决方案的打印性能, 以及丝网印刷、纤维形成和流量停止。最近的一些研究5、8、13清楚地表明, 可回收应变不一定与 laos 实验中施加的应变相同。例如, LAOS13下的软胶体玻璃研究发现, 当总应变明显较大时, 可回收应变仅为 5% (420%)。是强加的。其他研究16,21,22, 23,24使用保持架模量21也得出结论, 线性弹性可以在 laos 下观察到在点关闭对应变最大值, 这意味着材料在这些瞬间经历了相对较小的变形。SPP 方案是理解 LAOS 的唯一框架, laos 解释了应变平衡的变化, 导致可回收应变和总应变之间的差异。
本文的目的是通过提供 LAOS 分析免费软件的详细协议, 使用两种浓缩聚合物溶液, 4 wt% 黄原胶 (XG) 水溶液和 5 WT% PEO 在 DMSO 溶液中的理解和易用性。选择这些系统是因为它们具有广泛的应用范围和流变学上有趣的特性。黄原胶是一种天然的高分子量多糖, 是一种特别有效的水系统稳定剂, 通常用作食品添加剂, 以提供所需的粘化或在石油钻井中, 以增加粘度和屈服点。钻井泥巴。PEO 具有独特的亲水性, 经常用于医药产品和控释系统以及土壤修复活动。这些聚合物系统在各种振荡剪切条件下进行测试, 旨在近似加工、运输和最终使用条件。虽然这些实际条件不一定像振荡剪切那样涉及流动反转, 但在振荡测试中, 通过独立控制应用振幅和施加的频率, 可以很容易地逼近和调整流场。此外, SPP 方案可以按照此处所述用于了解范围广泛的流类型, 包括那些不包括流反转的流类型, 例如最近提出的 ULD-LAOS25, 其中大振幅振荡在一个仅指向 "单向 LAOS")。为了简单起见, 为了说明起见, 我们将当前的研究限制在传统的 LAOS, 它确实包括周期性的流反转。采用 SPP 方法对测量到的流变响应进行了分析。我们演示了如何使用 SPP 软件, 并对突出的计算步骤进行了简单的解释, 以提高读者的理解和使用。介绍了解释 SPP 分析结果的图例, 根据该图例确定了流变学过渡的类型。显示了两种聚合物在各种振荡剪切条件下的代表性 SPP 分析结果, 其中我们清楚地确定了一系列物理过程, 其中包含了材料的线性粘弹性响应信息以及材料的稳态流动特性。
该协议提供了如何准确执行非线性流变实验的突出细节, 以及使用 SPP 框架分析和理解流变响应的分步指南, 如图 1所示。我们首先介绍仪器的设置和校准, 然后是使商业上可用的流变仪收集高质量瞬态数据的特定命令。一旦获得流变数据, 我们就会介绍 SPP 分析免费软件, 并提供详细的手册。通过将 LAOS 得到的结果与线性状态频率扫描和稳态流动曲线进行比较, 进一步讨论了如何在 SPP 方案中了解两种浓缩聚合物溶液的时间依赖性响应。这些结果清楚地表明, 聚合物溶液在振荡中的不同流变状态之间过渡, 从而能够更详细地了解其非线性瞬态流变。这些数据可用于优化产品形成、运输和使用的处理条件。这些依赖时间的反应进一步提供了潜在的途径, 通过将流变学与从中子、x 射线或光线的小角度散射中获得的微观结构信息耦合起来, 形成清晰的结构-性质-处理关系 (SANS、SAXS 和 SALS)、显微镜或详细模拟。
Access restricted. Please log in or start a trial to view this content.
研究方案
1. 流变仪设置
- 使用在 SMT 模式下配置的流变仪 (参见注释), 连接上、下驱动几何形状。要保持尽可能接近均匀剪切场, 请使用50毫米板 (PP50) 作为下部夹具, 并使用2度锥形 (CP50-2) 作为上部夹具。
注意: 我们使用的流变仪 (见材料表) 可以配置为组合电机传感器 (cmt) 或单独的电机传感器 (smt) 模式。流变仪头只集成了一个电机, 它作为传统的 CMT 应力控制流变仪, 所获得的数据需要惯性校正。由于有两个电机集成在 SMT 模式中, 上部电机仅作为扭矩传感器运行, 而底部电机充当驱动单元, 从而将流变仪转换为典型的应变控制流变仪。- 连接底部和顶部的几何图形。
- 单击控制面板中的零间隙按钮。
- 在顶部的"测量集" 选项卡下导航以启动服务功能。运行上下测量系统的惯性校准, 可在下拉菜单中找到。
- 运行上下电机的调整。
- 在控制面板中指定所需的温度。
注: 在 XG 和 PEO 溶液上进行实验的测量结果分别为25±0.1°c 和35±0.1°c。
- 用铲子或移液器将感兴趣的材料装入底部几何形状的顶部, 确保样品中不包含气泡。
注: 在设置下的流变测量软件中提供了完全填充几何图形所需的材料的近似体积。测量系统。- 负载1.14 毫升以填充圆锥和板的几何形状。用铲子装入粘度较高的样品, 用移液器装载粘度较低的材料。
注: 铲子用于加载聚合物溶液。 - 命令测量系统修剪间隙, 并使用方形铲子轻轻修剪几何边缘的多余材料, 确保铲子保持垂直于流变仪的轴。
注: 材料装载质量将显著影响流变结果, 应避免任何明显的不足或过度灌装。 - 按流变测量软件中的继续按钮移动到测量间隙。
注意: 完整的加载过程如图 2所示。
- 负载1.14 毫升以填充圆锥和板的几何形状。用铲子装入粘度较高的样品, 用移液器装载粘度较低的材料。
2. 进行振荡剪切试验
注: 介绍了两种运行振荡剪切试验的方法。第一种方法仅针对正弦应力和应变而设计, 用于收集我们在此处报告的数据。第二种方法允许设置任意应力或应变计划。
-
正弦振荡剪切
- 导航到大振幅振荡剪切-Laos 下的我的应用程序在软件中。转到 "测量" 框, 然后单击应变变量。
- 指定初始值 (1%)和最终值 (4, 000%)应变振幅扫描。指定 0.316 rads 的施加频率. 将所需的应变振幅总数定义为指定振幅范围内的 16, 这将导致每 10年5点的点密度。
- 检查顶部的"获取波形" 框, 以收集瞬态响应。
- 单击顶部的"开始" 按钮开始实验, 原始数据将自动显示在流变测量软件中。
-
任意应力或应变计划
- 要施加任意定义的变形, 请单击软件中 "我的应用程序" 下的"波形正弦生成器".
- 定义与要应用的函数相对应的应变值列表 (不限于正弦波形)。在外部程序中生成值列表。
- 单击测量框中应变值下的"编辑" 。将这些数字复制并粘贴到值列表中。
- 指定数据点的数量、点持续时间和间隔时间, 以调整所施加的频率。例如, 如果将正弦应变周期粘贴到具有512个点的应变值列表中, 并且需要 1 rads 的频率, 则分别将数据点的数量和间隔时间指定为512点和 6.2832 s。
注意: 由于振荡循环次数有限, 也由于在流变仪上的振荡测试模式下启用的自动校正在本模式。尽管如此, 由于 SPP 框架中没有正弦应变的假设, 因此可以根据材料可能遇到的加工条件或最终用途任意定义施加的应变函数, 而 SPP 框架仍然存在适用于流变响应的分析。 - 检查顶部的"获取波形" 框。然后单击顶部的"开始" 按钮开始实验。
3. 执行 SPP 分析 (SPP-LAOS 软件)
注: SPP 分析软件是一个基于 matlab 的免费软件包, 用于分析与 SPP 框架的流变数据, 并作为补充文件 1 \ u2012621 附加.
- 将数据文件设置为制词条分隔的文本 (. txt), 由四列组成, 顺序为 {Time (-)、应变 (-)、速率 (-)、压力 (Pa)}。
注意: 用户可能需要修改函数文件中的标题行数, 以便能够处理其数据。请参阅示例数据文件 (补充文件 7\ o20120129)。 - 若要运行 SPP-LAOS 软件, 请在 MATLAB 中打开名为RunSPPplus_v1.m的 m 文件。
注意: 虽然 RunSPPplus_v1.m 是运行分析的主要脚本, 但包中包含将从主脚本调用的其他函数文件, 包括 SPPplus_read_v1.m、SPPplus_fourier_v1.m、SPPplus_numerical_v1.m、SPPplus_print_v1.m 和SPPplus_figure_v1.m. - 导航到标记为 "用户定义"变量的部分, 并指定以下变量。
- 文件名: 指定将用于 SPP 分析的. txt 文件的名称。
注意: 该文件必须符合上述格式要求。 - 运行状态: 将矢量作为 [1, 0] 运行傅立叶分析模式, 以实现规则的振荡剪切响应。
注: 该软件采用两种不同的方法来计算瞬时 SPP 模量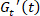 ,
, 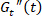 并基于傅立叶变换和数值微分。傅立叶变换方法是为周期输入而设计的, 如振荡剪切试验。任意时间相关测试, 包括但不限于正弦协议, 可以用数值微分方法进行分析。
并基于傅立叶变换和数值微分。傅立叶变换方法是为周期输入而设计的, 如振荡剪切试验。任意时间相关测试, 包括但不限于正弦协议, 可以用数值微分方法进行分析。 - 运行状态: 将矢量输入为 [0, 1] 以运行数字微分分析模式, 用于任意时间相关的测试。
- 欧米茄 (傅立叶分析): 用半径单位指定振荡的角频率。
- M (傅立叶分析): 定义要包含在 SPP 分析中的较高谐波数。调整这个数字, 以包括噪音地板上方所有较高的谐波。
注意: 此数字必须是正奇数, 并随振幅和材质的变化而变化。我们包括 MAOS 系统中的第三谐波, 以及所调查的最大振幅的第55次谐波。 - p (傅立叶分析): 指定输入数据中测量时间的总数, 它必须是正整数。
注意: 收集的数据周期越多, SPP 参数的时间分辨率就越高。 - k (数值微分): 定义数值微分的步长, 它必须是正整数。
- num _ mode (数值微分): 将num _ mode 指定为"0" (标准微分) 或 "1" (循环微分)。
注: 在数值微分方案中实现了两个过程。"标准区分" 没有对数据的形式作出假设。它利用正向差计算数据的前 2, 000个点的导数, 最后 2, 000个点的后向差, 以及其他地方的居中差。"循环微分" 假定数据是在稳态周期条件下获取的, 并包含一个整数的句点。这些假设允许通过在数据的两端循环来计算居中的差异。 - 指定所有变量后, 选择顶部的运行按钮。
注意: 软件将计算与数据关联的所有 SPP 指标, 然后显示与当前分析运行相关的数字, 并输出包含所有计算的 SPP 指标的文本文件, 以便进一步分析。 - 从输出傅里叶谱上迭代调整要包含在分析中的谐波数。包括噪音地板上方所有较高的奇次谐波。
- 文件名: 指定将用于 SPP 分析的. txt 文件的名称。
4. 解释 LAOS 响应
- 导航到瞬时 SPP 模数的
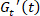 Cole-Cole 图,
Cole-Cole 图, 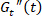 该图由 spp 软件自动生成。
该图由 spp 软件自动生成。
注: Cole-Cole 地块中的曲线被认为是粘弹性材料状态的轨迹, 在周期间过程中, 可以在振荡中、周期内过程中或连续周期之间形成解释。 - 用瞬时弹性模量解释刚度,
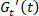 并增加/
并增加/ 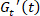 减少, 表明刚度/软化。请参见图 3。
减少, 表明刚度/软化。请参见图 3。 - 根据瞬时粘性模量解释材料的粘度
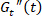 。此参数的减小表示增薄。
。此参数的减小表示增薄。 - 将焦点转移到瞬态模量的时间导数的另一个 Cole-Cole
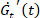 图
图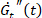 , 并提供有关响应变硬 (
, 并提供有关响应变硬 (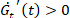 )、软化 ()、增厚 (
)、软化 ()、增厚 (
 ) 的定量信息,变薄 (
) 的定量信息,变薄 (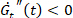 )。请参见图 3。
)。请参见图 3。
注: 利用导数的数值, 可以定量确定材料经过硬化度的速率/软化或增厚。 - 读取作为动态模
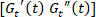

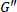 量的 cole-cole 图中的轨迹中心 (在时间加权平均意义上)。
量的 cole-cole 图中的轨迹中心 (在时间加权平均意义上)。
注意: 动态模量是变形周期内的平均参数, 不足以在 laos 下提供本地信息。 - 跟踪轨迹在振幅之间的相对运动, 以了解周期间的物理学。
注: 关注时间加权平均中心的相对运动, 相当于传统的动态模量的应变振幅扫描。尽管如此, 人们可以很容易地分析其他特定点的跨振幅运动, 例如应变极值。 - 确定瞬态微分粘
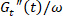 度, 并将其叠加在稳定剪切流曲线的顶部。比较瞬态 LAOS 响应与稳态剪切条件的对比。
度, 并将其叠加在稳定剪切流曲线的顶部。比较瞬态 LAOS 响应与稳态剪切条件的对比。 - 确定在 Cole-Cole 图中的大振幅处
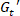
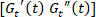 的最大值点。请参见图 4c中标记的星形。
的最大值点。请参见图 4c中标记的星形。- 记录这些瞬间的
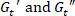 值。
值。 - 在动态模量的振幅扫描的基础上绘制它们。参见图 4d。
注意: 注意最大瞬态弹性模量与线性粘弹性 之间的任何对应关系。
之间的任何对应关系。
- 记录这些瞬间的
- 找到弹性 Llsajous 图形
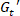 中最大的瞬间, 并记录相应的应变值。请参阅图 4a中标记的星形。
中最大的瞬间, 并记录相应的应变值。请参阅图 4a中标记的星形。 - 如果
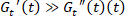 , 然后确定平衡应变和
, 然后确定平衡应变和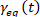 弹性应变.
弹性应变. 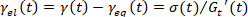
注意。在位移应力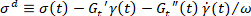 的作用下
的作用下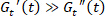 , 当平衡应变可以确定
, 当平衡应变可以确定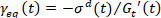 为, 因此弹性应变可以确定为应变和平衡应变 5, 13 之间的差异时, 可以确定..在其他地方
为, 因此弹性应变可以确定为应变和平衡应变 5, 13 之间的差异时, 可以确定..在其他地方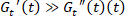 推导和讨论了这一要求。
推导和讨论了这一要求。 - 绘制弹性应变作为施加应变振幅的函数。参见图 4e。如果弹性应变与应变振幅无关, 则指示该临界应变在振幅扫描上, 如图4d 所示。
Access restricted. Please log in or start a trial to view this content.
结果
图 4和图 5给出了在振荡剪切试验下 xg 和 PEO/DMSO 溶液的 spp 分析的代表性结果。我们首先将原始数据呈现为弹性 (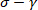 ) 和粘性 (
) 和粘性 (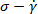 ) Lissajus-bowdcht 曲线, 如图 4a、 4a、 5a和5a。为了充分理解周期内物理, 图4c...
) Lissajus-bowdcht 曲线, 如图 4a、 4a、 5a和5a。为了充分理解周期内物理, 图4c...
Access restricted. Please log in or start a trial to view this content.
讨论
我们已经演示了如何正确地执行大振幅振荡剪切流变测试使用商业流变仪, 并运行 SPP 分析免费软件来解释和理解两个不同的聚合物解决方案的非线性应力响应。SPP 框架以前已被证明与结构变化相关, 并有助于了解许多胶体系统, 它同样适用于聚合物体系。利用 SPP 方案研究了两种浓缩聚合物溶液对 LAOS 的响应, 在 spp 方案中, 流变反应表现出复杂的过程序列。这些瞬态循环内解释提供了有关聚合物?...
Access restricted. Please log in or start a trial to view this content.
披露声明
作者没有什么可透露的。
致谢
作者感谢安东帕通过他们的 VIP 学术研究项目使用 MCR 702 流变仪。我们还感谢 Abhishek Shetty 博士在仪器设置中的评论。
Access restricted. Please log in or start a trial to view this content.
材料
| Name | Company | Catalog Number | Comments |
| SPP analysis software | Simon Rogers Group (UIUC) | SPPplus_v1p1 | Attached as supplementary files |
| MATLAB | Mathwork | ||
| Rheometer | Anton Paar | MCR 702 TwinDrive | |
| 50mm 2-degree cone | Anton Paar | CP50-2 | Upper measuring system |
| 50mm plate | Anton Paar | PP50 | Lower measuring system |
| Xanthan gum (XG) | Sigma-Aldrich | 11138-66-2 | |
| Polyethylene oxide (PEO) | Sigma-Aldrich | 25322-68-3 | Mv=1,000,000 |
| Dimethyl sulfoxide (DMSO) | Sigma-Aldrich | 67-68-5 |
参考文献
- Dolz, M., Hernández, M. J., Delegido, J., Alfaro, M. C., Muñoz, J. Influence of xanthan gum and locust bean gum upon flow and thixotropic behaviour of food emulsions containing modified starch. Journal of Food Engineering. 81 (1), 179-186 (2007).
- Gupta, N., Zeltmann, S. E., Shunmugasamy, V. C., Pinisetty, D. Applications of Polymer Matrix Syntactic Foams. JOM. 66 (2), 245-254 (2013).
- Garcıa-Ochoa, F., Santos, V. E., Casas, J. A., Gómez, E. Xanthan gum: production, recovery, and properties. Biotechnology Advances. 18 (7), 549-579 (2000).
- Chang, I., Im, J., Prasidhi, A. K., Cho, G. -C. Effects of Xanthan gum biopolymer on soil strengthening. Construction and Building Materials. 74, 65-72 (2015).
- Rogers, S. A. In search of physical meaning: defining transient parameters for nonlinear viscoelasticity. Rheologica Acta. 56 (5), 501-525 (2017).
- Ferry, J. D. Viscoelastic properties of polymers. , John Wiley & Sons. (1980).
- Bird, R. B., Armstrong, R. C., Hassager, O. Dynamics of Polymeric Liquids. Volume 1: Fluid Mechanics. , John Wiley & Sons. New York. (1987).
- Park, J. D., Rogers, S. A. The transient behavior of soft glassy materials far from equilibrium. Journal of Rheology. 62 (4), 869-888 (2018).
- Rogers, S., Kohlbrecher, J., Lettinga, M. P. The molecular origin of stress generation in worm-like micelles, using a rheo-SANS LAOS approach. Soft Matter. 8 (30), 7831-7839 (2012).
- Lettinga, M. P., Holmqvist, P., Ballesta, P., Rogers, S., Kleshchanok, D., Struth, B. Nonlinear Behavior of Nematic Platelet Dispersions in Shear Flow. Phys Rev Lett. 109 (24), 246001(2012).
- Hyun, K., Wilhelm, M., et al. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Progress in Polymer Science. 36 (12), 1697-1753 (2011).
- Park, J. D., Ahn, K. H., Lee, S. J. Structural change and dynamics of colloidal gels under oscillatory shear flow. Soft Matter. 11 (48), 9262-9272 (2015).
- Lee, C. -W., Rogers, S. A. A sequence of physical processes quantified in LAOS by continuous local measures. Korea-Australia Rheology Journal. 29 (4), 269-279 (2017).
- Rogers, S. A., Erwin, B. M., Vlassopoulos, D., Cloitre, M. A sequence of physical processes determined and quantified in LAOS: Application to a yield stress fluid. Journal of Rheology. 55 (2), 435-458 (2011).
- Wagner, M. H., Rolon-Garrido, V. H., Hyun, K., Wilhelm, M. Analysis of medium amplitude oscillatory shear data of entangled linear and model comb polymers. Journal of Rheology. 55 (3), 495-516 (2011).
- Radhakrishnan, R., Fielding, S. Shear banding in large amplitude oscillatory shear (LAOStrain and LAOStress) of soft glassy materials. Journal of Rheology. 62 (2), 559-576 (2018).
- Bharadwaj, N. A., Ewoldt, R. H. Constitutive model fingerprints in medium-amplitude oscillatory shear. Journal of Rheology. 59 (2), 557-592 (2015).
- Wilhelm, M. Fourier‐Transform Rheology. Macromolecular Materials and Engineering. 287 (2), 83-105 (2002).
- Ewoldt, R. H., Hosoi, A. E., McKinley, G. H. New measures for characterizing nonlinear viscoelasticity in large amplitude oscillatory shear. Journal of Rheology. 52 (6), 1427-1458 (2008).
- Rogers, S. A., Lettinga, M. P. A sequence of physical processes determined and quantified in large-amplitude oscillatory shear (LAOS): Application to theoretical nonlinear models. Journal of Rheology. 56 (1), 1-25 (2011).
- Rogers, S. A. A sequence of physical processes determined and quantified in LAOS: An instantaneous local 2D/3D approach. Journal of Rheology. 56 (5), 1129-1151 (2012).
- Kim, J., Merger, D., Wilhelm, M., Helgeson, M. E. Microstructure and nonlinear signatures of yielding in a heterogeneous colloidal gel under large amplitude oscillatory shear. Journal of Rheology. 58 (5), 1359-1390 (2014).
- van der Vaart, K., Rahmani, Y., Zargar, R., Hu, Z., Bonn, D., Schall, P. Rheology of concentrated soft and hard-sphere suspensions. Journal of Rheology. 57 (4), 1195-1209 (2013).
- Poulos, A. S., Stellbrink, J., Petekidis, G. Flow of concentrated solutions of starlike micelles under large-amplitude oscillatory shear. Rheologica Acta. 52 (8-9), 785-800 (2013).
- Armstrong, M. J., Beris, A. N., Rogers, S. A., Wagner, N. J. Dynamic shear rheology of a thixotropic suspension: Comparison of an improved structure-based model with large amplitude oscillatory shear experiments. Journal of Rheology. 60 (3), 433-450 (2016).
- Calabrese, M. A., Wagner, N. J., Rogers, S. A. An optimized protocol for the analysis of time-resolved elastic scattering experiments. Soft Matter. 12 (8), 2301-2308 (2016).
Access restricted. Please log in or start a trial to view this content.
转载和许可
请求许可使用此 JoVE 文章的文本或图形
请求许可This article has been published
Video Coming Soon
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。