JoVE Logo
Authors
Contact Us

Sign In

A subscription to JoVE is required to view this content. Sign in or start your free trial.

In This Article

  • Summary
  • Abstract
  • Introduction
  • Protocol
  • תוצאות
  • Discussion
  • Disclosures
  • Acknowledgements
  • Materials
  • References
  • Reprints and Permissions

Summary

אנו מציגים פרוטוקול מפורט חלוקה לרמות ביצוע rheology לא לינארית הטיה מתנדנדות על חומרים רכים, וכיצד להפעיל את ניתוח SPP-לאוס כדי להבין את התגובות כרצף של תהליכים פיזיקליים.

Abstract

אנחנו חוקרים את הרצף של תהליכים פיזיקליים הציג במהלך משרעת גדולה מתנדנדות הטיה (לאוס) של תחמוצת פוליאתילן (פאו) דימתיל סולפוקסיד (דימתיל סולפוקסיד), xanthan מסטיק במים – שני מרוכז תמיסות פולימר משמש viscosifiers במזונות, שחזור משופר שמן, משיקום קרקע. הבנת ההתנהגות rheological לא לינארית מחומרים קלים חשוב בעיצוב, נשלט הייצור של מוצרי צריכה רבים. הוא הראה כיצד אפשר לפרש התגובה לאוס הפתרונות הללו פולימר מבחינת מעבר ברור מן viscoelasticity ליניארית דפורמציה viscoplastic וחזרה שוב במהלך תקופה. התוצאות לאוס הן שנותחה באמצעות הטכניקה במלואה כמותיים רצף של תהליכים פיזיים (SPP), באמצעות תוכנה חופשית מבוססת-MATLAB. נוהל מפורט של ביצוע מדידה לאוס עם rheometer המסחרי ניתוח תגובות הלחץ לא לינארית עם freeware, ופרשנות תהליכים פיזיקליים תחת לאוס מוצג. היא מופיעה בהמשך, במסגרת SPP, תגובה לאוס מכיל מידע לגבי viscoelasticity לינארי את העקומות זרימה ארעי, המתח קריטי אחראי על תחילתה של nonlinearity.

Introduction

מרוכז תמיסות פולימרים משמשים במגוון רחב של יישומים תעשייתיים בעיקר להגברת צמיגות, לרבות מזונות1 ו אחרים מוצרים לצרכן2, שחזור שמן משופרת3ואדמה תיקונים4. במהלך עיבוד ושימוש שלהם, הם בהכרח נידונים דפורמציות גדולות על טווח של צירי זמן. תחת תהליכים כאלה, הם מדגימים עשיר לא לינארית rheological והתנהגויות מורכבות התלויים זרימה או דפורמציה תנאים1. להבנת התנהגויות מורכבות rheological לא לינארית חיוני בהצלחה שליטה תהליכים, תכנון מוצרים מעולים של למקסם יעילות אנרגיה. מלבד החשיבות תעשייתי, יש מידה רבה של עניין אקדמי בהבנת ההתנהגויות rheological של חומרים פולימריים רחוק שיווי משקל.

הטיה מתנדנדות בדיקות הן מרכיב בסיסי של כל אפיון rheological יסודית בשל היישום אורתוגונלית של זן ו זן שיעור5, היכולת לשלוט באופן עצמאי את האורך ואת הזמן מאזני הנייר על-ידי כיוונון משרעת ותדירות. תגובת המתח זנים הטיה מתנדנדות משרעת קטן, אשר הם קטנים מספיק כדי שלא להפריע את המבנה הפנימי של חומר, יכול להיות לרכיבים בשלב עם המתח, בשלב עם קצב זן. המקדמים של הרכיבים בשלב עם המתח וקצב זן באופן קולקטיבי מתייחסים כמו מודולים דינמיים6,7, ובנפרד כמו המודולוס אחסון, figure-introduction-1290 , ואת אובדן המודולוס, figure-introduction-1384 . 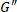מודולים דינמיים להוביל נקה פרשנויות אלסטיות וחוזק צמיגה. עם זאת, פרשנויות בהתבסס על מודולים דינמיים אלה תקפים רק עבור amplitudes זן קטן, שבו מתח התגובות sinusoidal excitations גם הם sinusoidal. המשטר בדרך כלל מתייחסים כאל משרעת קטן מתנדנדות גזירה (SAOS) או המשטר viscoelastic ליניארית. להרכב שנכפה עליו הופך גדול יותר, השינויים הם המושרה ב מיקרו חומרים, אשר משתקפים בסיבוכיות של תגובות הלחץ חולף שאינו sinusoidal8. במשטר זה rheologically לא-ליניאריות, אשר באופן הדוק יותר מחקה בתנאי שימוש תעשייתי של עיבוד של הצרכן, לשמש מודולים דינמיים המסכן תיאורים של התגובה. דרך אחרת להבין כמה חומרים רכים מרוכז מתנהגים מתוך שיווי משקל ולכן נדרש.

מספר האחרונות מחקרים9,10,11,12,13,14,15,16 הראו כי חומרים יעברו דרך שינויים מבניים, דינמיות מגוונות אינטרה-מחזור שהפיק דפורמציות גדולות משרעת בינוני מתנדנדות הטיה (MAOS)15,17 ו הטיה מתנדנדות משרעת גדולה משטרים (לאוס). השינויים המבניים, דינמיות אינטרה-מחזור יש ביטויים שונים, כגון שבירה של מיקרו, חיזקו מבניים, rearrangements מקומיים, הרפורמציה ושינויים diffusivity. אלה שינויים פיזיים אינטרה-מחזור המשטר לא לינארית להוביל התגובות מתח לא לינארית מורכבים לא יכול להתפרש בפשטות עם מודולים דינמיים. כחלופה, מספר גישות שהוצעו על הפרשנות של התגובות מתח לא-ליניאריות. דוגמאות נפוצות של זה הן פורייה המרה rheology (rheology מטרים)18, טור חזקות הרחבות11, תיאור צ'בישב19, ואודות הרצף של תהליכים פיזיקליים (SPP)5,8, 13,14,20 ניתוח. למרות כל הטכניקות הללו הוכחו להיות עמיד מבחינה מתמטית, זה עדיין שאלה ללא מענה לגבי אם באחת מהשיטות הבאות יכול לספק הסברים פיזי ברור והגיוני של תגובות הלחץ מתנדנדות לא-ליניאריות. זה נשאר אתגר מצטיינים להעניק פרשנויות תמציתי של נתונים rheological תשבחות אמצעים מבניים דינמיות.

במחקר שנערך לאחרונה, תגובת המתח לא לינארית של מודל Rheology מזוגגות רכות (SGR)8 וכוס רך העשוי colloidal פולימרים כוכב7תחת הטיה מתנדנדות נותחו באמצעות ערכת SPP. טמפורלית שינויים במאפייני אלסטיות וחוזק צמיגה הטמונה תגובות הלחץ לא לינארית היו לכמת בנפרד על-ידי מודולים SPP, 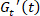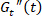figure-introduction-4052 , figure-introduction-4120 . יתר על כן, המעבר rheological המיוצג על-ידי מודולים ארעי היה בקורלציה במדויק לשינויים microstructural מיוצגים על ידי חלוקת אלמנטים mesoscopic. במחקר של מודל SGR8, זה בבירור הראו שכי פרשנות rheological באמצעות ערכת SPP משקף באופן מדויק השינויים הגופניים תחת בכל התנאים הטיה מתנדנדות המשטרים ליניאריים ולא -ליניאריים משקפי שמש רכה. יכולת ייחודית זו לספק מדויק הפירוש הפיזיקלי של תגובות לא לינארית של משקפיים רך הופך השיטה SPP גישה אטרקטיבי עבור החוקרים ללמוד out-של-שיווי משקל הדינמיקה של תמיסות פולימר וחומרים רכים אחרים.

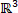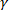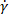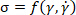ערכת SPP בנוי סביב הצגת התנהגויות rheological כפי שקורה במרחב תלת-ממדי (figure-introduction-4847) כולל המתח (figure-introduction-4925), זן קצב (figure-introduction-5001), מתח (figure-introduction-5074)5. במובן המתמטי, תגובות הלחץ כאל פונקציות multivariable של זן ו זן קצב (figure-introduction-5236). כמו ההתנהגות rheological נחשב מסלול ב 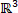figure-introduction-5342 (או פונקציה multivariable), כלי דנים את המאפיינים של מסלול נדרש. בגישה SPP, מודולים ארעית 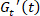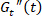figure-introduction-5498 , figure-introduction-5566 ככזה. הנפח ארעית 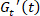figure-introduction-5649 , מודולוס צמיגה 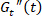figure-introduction-5731 מוגדרים נגזרות חלקיות של הלחץ ביחס המתח (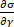figure-introduction-5838) וקצב זן (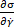figure-introduction-5916). בעקבות ההגדרה הפיזי של מודולים אלסטיות וחוזק צמיגה דיפרנציאלית, מודולים ארעי לכמת השפעתה מיידית של זן וקצב המתח על תגובת המתח בהתאמה, ואילו שיטות ניתוח אחרות אין אפשרות לספק את כל מידע על תכונות אלסטיות וחוזק צמיגה בנפרד.

הגישה SPP מעשיר את הפרשנות של הבדיקות הטיה מתנדנדות. עם הניתוח של SPP, התנהגויות מורכבות rheological לא לינארית של תמיסות פולימרים מרוכז בלאוס אפשר קשורה ישירות ההתנהגויות rheological ליניארית ב- SAOS. אנחנו מראים בעבודה זו איך מרבית הנפח ארעי (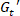figure-introduction-6481מקסימום) ליד המתח extrema מקביל המודולוס אחסון המשטר ליניארי (SAOS). יתר על כן, אנו מציגים כיצד המודולוס צמיגה ארעי (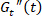figure-introduction-6676) במהלך לאוס מחזור רשמים עקומת זרימה מצב יציב. בנוסף מתן פרטים של רצף מורכב של תהליכים מרוכז תמיסות פולימר לעבור תחת לאוס, ערכת SPP מספק גם את המידע לגבי המתח ההשבה בחומר. מידע זה, שאינו בר השגה דרך גישות אחרות, הוא מדד שימושי של כמה חומר יירתע ברגע מתח יוסר. התנהגות כזו יש השפעה על שמשטחו הפתרונות מרוכז עבור יישומי הדפסה תלת-ממדית, וכן הדפסה המסך, סיבים היווצרות הפסקת זרימת. מספר מחקרים שנערכו לאחרונה,5,8,13 עולה בבירור כי המתח ההשבה היא לא בהכרח זהה המתח שהוטלו במהלך הניסויים לאוס. למשל, מחקר של משקפיים colloidal רך לפי לאוס13 מצאו כי המתח ההשבה הוא רק 5% כאשר משמעותית גדול יותר הכולל זן (420%) הוא הטיל. מחקרים אחרים16,21,22,23,24 באמצעות מודולוס21 את הכלוב גם להסיק אלסטיות ליניארי יכול להיות שנצפו תחת לאוס בנקודת סגור בן ציון לזר זן, רומז כי החומרים חוו דפורמציה קטן יחסית על הרגעים האלה. ערכת SPP הוא המסגרת היחידה ללאוס הבנה החשבונות עבור משמרת באיזון עומס שמוביל הבדל בין ההשבה של זנים הכולל.

מאמר זה נועד להקל על ההבנות ואת קלות השימוש של שיטת הניתוח SPP על-ידי מתן פרוטוקול מפורט freeware ניתוח לאוס, באמצעות שתי תמיסות פולימר מרוכז, עם 4 wt % xanthan מסטיק (XG) תמיסה מימית של 5% wt פאו בפתרון דימתיל סולפוקסיד. מערכות אלו נבחרו בגלל שלהם במגוון רחב של יישומים ומעניין rheologically מאפיינים. Xanthan מסטיק, הצפוני רב גבוהה משקל מולקולרי-סוכר טבעי, הוא מייצב ביעילותן מערכות מימית והחלת נפוץ בתור תוסף לספק viscosification הרצוי מזון או בשמן קידוח להגדיל צמיגות, תשואות נקודות קידוח כושים. פאו יש מאפיין ייחודי הידרופילית ומשמש לעיתים קרובות מוצרים פרמצבטיים, מערכות לשחרור מבוקר, כמו גם פעילויות משיקום קרקע. מערכות פולימרים אלה נבחנים בתנאים הטיה מתנדנדות שונים שנועדו משוער עיבוד, תחבורה והתנאים ביתי. למרות אלה תנאים מעשיים ייתכן כרוך בהכרח היפוך זרימה כמו הטיה מתנדנדות, השדה זרימה ניתן בקלות לקרב את ערכיהן מכוון עם שליטה עצמאית של משרעת יישומית, שהוטלו תדירות במבחן מתנדנדות. יתר על כן, ערכת SPP יכול לשמש כפי שמתואר כאן להבין מגוון רחב של סוגי זרימה, לרבות אלה שאינן כוללות זרימת ביטולי כגון הציעה לאחרונה אוד-לאוס25, שבו מוחלות תנודות משרעת גדולה אחת רק בכיוון (המוביל הכינוי "לאוס חד-כיוונית"). לשם הפשטות, ולשם המחשה, אנחנו מגבילים המחקר הנוכחי לאוס המסורתית, הכוללים היפוך זרימה תקופתיים. התגובות rheological נמדד מנותחים עם הגישה SPP. נדגים כיצד להשתמש בתוכנה SPP עם הסברים בסיסיים על חישוב הבולטות צעדים כדי לשפר את ההבנה והשימוש הקוראים. מקרא לפרש את התוצאות של ניתוח SPP הוא הציג, על-פי אשר סוג מעבר rheological מזוהה. תוצאות ניתוח SPP נציג פולימרים שני בתנאים הטיה מתנדנדות שונים מוצגים, שבו נוכל לזהות בבירור רצף של תהליכים פיזיקליים, המכיל מידע על התגובה viscoelastic ליניארית של החומר כמו גם המאפיינים מצב יציב זרימה של החומר.

פרוטוקול זה מספק פרטים הבולטות של כיצד לבצע במדויק לא לינארית ניסויים rheological, כמו גם צעד אחר צעד מדריך כדי ניתוח והבנה rheological תגובות עם SPP framework, כפי שמוצג באיור1. נתחיל על-ידי מתן מבוא לכלי המהיר וההתקנה ולידציות, ואחריו פקודות ספציפיות עבור ביצוע של rheometer זמין מסחרית לאסוף נתונים ארעית באיכות גבוהה. ברגע שהנתונים rheological הושגו, אנחנו מציגים freeware ניתוח SPP, עם מדריך מפורט. יתר על כן, נדון כיצד להבין את התגובה תלוי-זמן של שני פתרונות פולימרים מרוכז בתוך ערכת SPP, על ידי השוואת התוצאות המתקבלות מלאוס לטאטא את תדירות ליניארי-המשטר, עקומת זרימה מצב יציב. תוצאות אלו לזהות בבירור כי הפתרונות פולימר מעבר בין מצבי rheological נפרדות בתוך תנודה, המאפשרות תמונה מפורטת יותר של שלהם rheology ארעית לא לינארית להסתמן. נתונים אלה ניתן להשתמש כדי למטב את תנאי עיבוד מוצר למערך, תחבורה, ולהשתמש. אלה תלוית זמן תגובות נוספות לספק מסלולים פוטנציאליים לטופס בבירור יחסי מבנה-רכוש-עיבוד על ידי צימוד rheology עם microstructural מידע שהתקבל זווית קטנה פיזור של נייטרונים, צילומי רנטגן או (אור SANS SAXS, SALS, בהתאמה), מיקרוסקופיה, או סימולציות מפורט.

Access restricted. Please log in or start a trial to view this content.

Protocol

1. rheometer ההתקנה

  1. עם rheometer נקבעה במצב של טכנולוגיית השמה משטחית (ראה הערה), לצרף את גיאומטריות הכונן העליון והתחתון. כדי לשמור על כמה שיותר קרוב שדה הטיה הומוגניות ככל האפשר, השתמש צלחת 50 מ מ (PP50) הנורה התחתון, וכן קונוס 2 מעלות (CP50-2) עבור הנורה העליון.
    הערה: rheometer אנו משתמשים (ראה הטבלה של חומרים) ניתן להגדיר גם בשילוב מנוע-מתמר (CMT) או במצב מתמר מנוע נפרד (SMT). עם רק מנוע יחיד משולב בראש rheometer, היא פועלת כמו המסורתי CMT שבשליטת הלחץ rheometer, הנתונים שהושגו דורשת אינרציה תיקונים. עם שני מנועים שולבו במצב SMT, המנוע העליון פועל אך ורק מתמר מומנט, המנוע התחתון פועל כיחידה נסיעה וכך המרת את rheometer rheometer טיפוסי שבשליטת זן.
    1. לצרף את גיאומטריות תחתון ועליון.
    2. לחץ על לחצן אפס-gap שבלוח הבקרה.
    3. נווט כדי להפעיל פונקציה שירות תחת הכרטיסייה ערכת מדידה על העליונה. להפעיל כוח האינרציה ולידציות עבור העליון והתחתון, מדידה, מצאתי בתפריט הנפתח.
    4. הפעל את ההתאמות מנועים עליון ותחתון.
    5. ציין את הטמפרטורה הרצויה בחלונית ' בקרה '.
      הערה: המידות-אילו ניסויים XG ו פאו מבוצעות פתרונות הם 25 ± 0.1 º C ו 35 ± 0.1 º C בהתאמה.
  2. לטעון את החומר של עניין על-גבי הצורה הגיאומטרית התחתון עם מרית או פיפטה, המבטיח שאין בועות אוויר הם entrained במדגם.
    הערה: כרכים משוער של החומר הנדרש למלא לגמרי על גאומטריה ניתנים התוכנה rheometry תחת הגדרת | , מדידה.
    1. לטעון mL 1.14 כדי למלא את הגיאומטריה של קונוס-צלחת. לטעון דגימות צמיגות גבוהה יותר עם מרית, ופחות צמיגה חומרים עם פיפטה.
      הערה: מרית משמש כדי לטעון את הפתרונות פולימר.
    2. הפקודה מערכת מדידה כדי לקצץ את הפער ולחיתוך בעדינות חומר עודף בקצה של גיאומטריה עם מרית הסתיימה כיכר, הבטחת שהמרית נשאר בניצב לציר rheometer.
      הערה: איכות החומרים טעינת ישפיעו על התוצאות rheological באופן משמעותי, יש לכאורה תחת - או over - filling יש להימנע.
    3. לחץ על לחצן המשך בתוכנה rheometry כדי להעביר המדידה הפער.
      הערה: תהליך טעינה מלאה מודגם באיור2.

2. בדיקות הטיה מתנדנדות

הערה: הם הציגו שתי דרכים של בדיקות הטיה מתנדנדות. הגישה הראשונה מיועדת sinusoidal מדגיש וללחצים רק ושימש כדי לאסוף את הנתונים שאנחנו מדווחים כאן. השיטה השניה מאפשרת מתח שרירותי או לוחות זמנים זן להגדיר.

  1. הטיה מתנדנדות sinusoidal
    1. נווט אל משרעת גדולה מתנדנדות הטיה-לאוס תחת שלי apps בתוכנה. עבור תיבת מדידה ולחץ מתח משתנה.
    2. לציין הראשונית (1%) ואת הערכים הסופיים (4000%) של סריקה משרעת המתח. לציין את התדירות שנכפה עליו של ראד 0.316/s. הגדר המספר הכולל הרצוי של זן amplitudes כמו 16 בטווח שצוין משרעת, כשהתוצאה היא הצפיפות בנקודה של 5 נקודות לכל עשור.
    3. סמן את התיבה לקבל waveform בחלק העליון כדי לאסוף את התגובות ארעית.
    4. לחץ על לחצן ' התחל ' בחלק העליון כדי להפעיל את הניסויים, הנתונים הגולמיים יוצגו בתוכנה rheometry באופן אוטומטי.
  2. מתח שרירותי או לוחות זמנים זן
    1. לכפות שרירותי מוגדרת על-ידי דפורמציה, לחץ על צורת גל סינוס מחולל תחת שלי apps בתוכנה.
    2. להגדיר רשימה של ערכי המתח המתאימים לפונקציה זו כדי להחיל (לא מוגבל sinusoidal waveform). צור רשימת הערכים בתוכנית חיצוניים.
    3. לחץ על ערוך תחת הערך זן בתיבה מדידה. העתק והדבק את המספרים האלה לתוך רשימת ערכים.
    4. ציין את מספר נקודות הנתונים, הצבע ומשך מרווח הזמן כדי להתאים את תדירות שנכפה עליו. כך למשל, מציינים את מספר נקודות הנתונים ואת מרווח הזמן 512 נקודות וכן 6.2832 s, בהתאמה, אם מחזור של זן sinusoidal יודבק זן רשימת ערכים עם 512 נקודות ואת התדירות של ראד 1/s היא הרצויה.
      הערה: גישה זו אינה מומלצת עבור הפעלת הטיה מתנדנדות sinusoidal בגלל מספר מוגבל של מחזורי מתנדנדות, וגם בשל העובדה כי התיקונים האוטומטיים אשר זמינות במצב בדיקה מתנדנדות על rheometer מושבתים בזה מצב זה. למרות זאת, מאחר שאיני של זן sinusoidal מובנה בתוך המסגרת SPP, ניתן באופן שרירותי להגדיר פונקציות זן שנכפה עליו על-פי התנאים עיבוד או סוף להשתמש החומרים עלולים לחוות, שרידי מסגרת SPP כדי לנתח את התגובה rheological הישימים.
    5. סמן את התיבה לקבל waveform בחלק העליון. לחץ על לחצן ' התחל ' בחלק העליון כדי להפעיל את הניסויים.

3. ביצוע ניתוח SPP (תוכנה SPP-לאוס)

הערה: התוכנה ניתוח SPP חבילה מבוסס-MATLAB freeware עבור ניתוח נתונים rheological בעזרת מסגרת SPP, מצורפת כמו הקבצים המשלימים 1\u2012621.

  1. לעצב את קבצי הנתונים להיות טקסט מופרד (. txt) בהיקף של ארבע עמודות מנת של {זמן (s), זן (-), קצב (1/s), מתח (Pa)}.
    הערה: משתמשים ייתכן שיהיה עליך לשנות את מספר שורות הכותרת קבצים פונקציה כדי להיות מסוגל לעבד את הנתונים שלהם. לראות קבצי נתונים לדוגמה (7\u20129 הקבצים המשלימים).
  2. כדי להפעיל תוכנה SPP-לאוס, פתח את m-הקובץ בשם RunSPPplus_v1.m ב- MATLAB.
    הערה: בעוד RunSPPplus_v1.m הוא קובץ ה-script הראשי כדי להפעיל את הניתוח, החבילה מכילה קבצים אחרים פונקציה אשר נקראת מהתסריט הראשי, כולל SPPplus_read_v1.m, SPPplus_fourier_v1.m, SPPplus_numerical_v1.m, SPPplus_print_v1.m, SPPplus_figure_v1.m.
  3. נווט אל המקטע שכותרתו משתנים על-ידי המשתמש, וציין את המשתנים הבאים.
    1. שם הקובץ: ציין את השם של קובץ. txt ישמש לניתוח SPP.
      הערה: הקובץ חייב להתאים את הדרישה בפורמט הנ.
    2. הפעל מצב: למקם את הווקטור כמו [1, 0] כדי להפעיל מצב אנליזת פורייה עבור התגובה הטיה מתנדנדות רגיל.
      הערה: התוכנה מעסיקה שתי שיטות שונות של חישוב של מודולים SPP מיידי,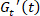 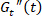figure-protocol-5765 , figure-protocol-5833 , המבוססת על שינוי פורייה, בידול מספריים. הגישה התמרת פורייה מיועד עבור קלט תקופתיים, כגון בדיקות הטיה מתנדנדות. מבחנים תלויי-זמן שרירותי, אשר כוללים, אך אינם מוגבלים פרוטוקולים sinusoidal, ניתן לנתח בגישה בידול מספריים.
    3. הפעל מצב: קלט את הווקטור כמו [0, 1] כדי להפעיל מצב אנליזה נומרית-בידול לבדיקות תלויי-זמן שרירותי.
    4. אומגה (ניתוח פורייה): לציין את תדירות זוויתית של תנודה, עם יחידות של ראד/s.
    5. M (ניתוח פורייה): להגדיר מספר הרמוניות גבוהות כדי להיכלל בניתוח SPP. התאם את המספר הזה כדי לכלול את כל הרמוניות גבוהות מעל הרצפה רעש.
      הערה: מספר זה חייב להיות מספר אי-זוגי חיובי, משתנה עם משרעת והחומרים. אנו כוללים עד היום ה-3 הרמונית המשטר MAOS, ועד 55 הרמונית-משרעת הגדול חקר.
    6. p (ניתוח פורייה): לציין את המספר הכולל של תקופות של מדידת הזמן בנתוני הקלט, אשר חייב להיות מספר שלם חיובי.
      הערה: בתקופות יותר של הנתונים שנאספו, ככל שהרזולוציה זמן של הפרמטרים SPP.
    7. k (בידול מספרי): להגדיר את גודל צעד עבור בידול מספריים, אשר חייב להיות מספר שלם חיובי.
    8. num_mode (בידול מספרי): ציין num_mode יהיה "0" (בידול סטנדרטי) או "1" (בידול שיכורה).
      הערה: ישנם שני הליכים ליישם את הערכה מספרית בידול. "בידול סטנדרטי" עושה בלי השערות לגבי צורתם של הנתונים. הוא מנצל את ההבדל קדימה כדי לחשב את הנגזרת על הנקודות 2,000 הראשונה של הנתונים, הבדל לאחור על 2,000 הנקודות הסופי הבדל ממורכז במקום אחר. "כרך בידול" מבוסס על ההנחה כי הנתונים נלקח בתנאים תקופתיים מצב יציב כוללת מספר שלם של תקופות. הנחות אלו מאפשרות הבדל ממורכז לחשב בכל מקום על-ידי יצירת לולאה על הקצוות של הנתונים.
    9. בחר בלחצן הפעל בראש ברגע כל המשתנים שצוינו.
      הערה: התוכנה לחשב כל המדדים SPP המשויך את הנתונים, ולאחר מכן להציג דמויות הקשורות במנוסה ניתוח הנוכחי, פלט קובץ טקסט המכיל כל מחושב SPP מדדים לצורך ניתוח נוסף.
    10. Iteratively לכוונן את מספר הרמוניות כדי להיכלל בניתוח מהפלט ספקטרום פורייה. כוללים כל הרמוניות מוזר גבוה מעל הרצפה רעש.

4. פירוש לתגובה לאוס

  1. נווט אל העלילה קול-קול של מודולים SPP מיידי 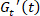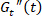figure-protocol-7935 , figure-protocol-8003 זה נוצר באופן אוטומטי על ידי תוכנת SPP.
    הערה: עיקול בעלילה קול-קול נחשב את המסלול של המדינה viscoelastic גשמי, פרשנויות יכול להיווצר בתוך תנודה, בתהליכים אינטרה-מחזור, או בין תקופות רצופות, תהליכים בין-מחזור.
  2. לפרש נוקשות על ידי הנפח מיידי,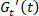figure-protocol-8321, הגדלה/הקטנה של 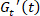figure-protocol-8405 המציין stiffening/ריכוך. ראו איור 3.
  3. לפרש צמיגות של חומר בהתבסס על המודולוס צמיגה מיידי, 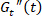figure-protocol-8600 . הגדלה/הקטנה פרמטר זה מייצג עיבוי/דליל.
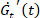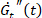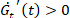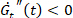  4. להעביר את המוקד אל קול-קול אחר, חלקת הזמן נגזרות של מודולים ארעית figure-protocol-8789 , figure-protocol-8859 , אשר מספקים מידע כמותי אודות כמה לתגובה הוא stiffening (figure-protocol-8990), ריכוך (figure-protocol-9067), עיבוי (figure-protocol-9144), דליל ((figure-protocol-9221)). ראו איור 3.
    הערה: עם הערכים של נגזרות, הקצב שבו עוברים חומרי ריכוך/stiffening או עיבוי/דליל יכול באופן כמותי להיקבע.
  5. . קראתי מרכז מסלול (במובן זמן משוקלל ממוצע) העלילה קול-קול של 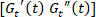figure-protocol-9514 כמו מודולים דינמיים, [figure-protocol-9604figure-protocol-9669].
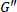    הערה: מודולים דינמיים הם בממוצע פרמטרים על מחזור של דפורמציה, אינן מספיקות לספק מידע מקומי תחת לאוס.
  6. לעקוב אחר התנועה היחסי של המסלול מעבר amplitudes להבין את הפיזיקה הבין-מחזור.
    הערה: התמקדות התנועה היחסית של מרכז ממוצע משוקלל זמן זה שקול לסריקה משרעת המתח המסורתי מודולים דינמיים. בכל זאת, אחד בקלות ניתן לנתח את התנועה על פני-משרעת של נקודות ספציפיות אחרות, למשל, extrema זן.
  7. לקבוע את צמיגות דיפרנציאלית ארעית 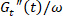figure-protocol-10195 רבדים זה על גבי עקומת זרימה יציבה-הטיה. להשוות את התגובה לאוס ארעי בתנאים יציב-הטיה.
  8. לקבוע את נקודות מקסימום 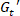figure-protocol-10382 ב amplitudes גדולים בעלילה קול-קול של 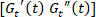figure-protocol-10488 . לראות את כוכב הנקרא איור 4ג'.
    1. להקליט את הערכים של 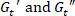figure-protocol-10652 על הרגעים האלה.
    2. מניחים אותם על גבי לטאטא את משרעת של מודולים דינמיים. ראו איור 4 d.
      הערה: שימו לב כל תכתובת בין את הנפח ארעי המרבי של viscoelastic ליניארי figure-protocol-10919 .
  9. לאתר את הרגעים של מקסימום 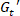figure-protocol-11042 ב הגומי Lissajous להבין ולהקליט את הערכים זן. לראות את כוכב המסומנות באיור 4a.
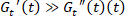  10. אם figure-protocol-11232 , לאחר מכן לקבוע את המתח שיווי משקל 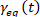figure-protocol-11342 ואת המתח אלסטי figure-protocol-11425 .
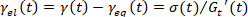    שימו לב. עם הלחץ הזחה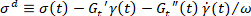 figure-protocol-11526 , כאשר 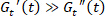figure-protocol-11607 המתח שיווי משקל יכול להיקבע כמו 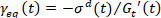figure-protocol-11707 , לפיכך ניתן לקבוע את המתח אלסטי כמו ההבדל בין זן שיווי משקל זן5,13 . הדרישה של 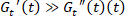figure-protocol-11914 נגזר ודן15במקום אחר.
  11. מגרש המתח אלסטי כפונקציה של משרעת המתח שנכפה עליו. ראה איור 4e. אם המתח אלסטית באופן עצמאי משרעת המתח, ואז מציינים את הנבג קריטיים לטאטא את משרעת כמו באיור 4 d.

Access restricted. Please log in or start a trial to view this content.

תוצאות

נציג תוצאות הניתוח SPP מ XG ופתרונות פאו/דימתיל סולפוקסיד תחת הטיה מתנדנדות בדיקות מוצגים איורים 4 ו- 5. תחילה נציג את הנתונים הגולמיים כמו אלסטית (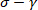figure-results-240), צמיגה (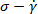figure-results-317) Lissajous-Bowditch עקומות דמוי...

Access restricted. Please log in or start a trial to view this content.

Discussion

הראו כיצד לבצע כראוי משרעת גדולה הטיה מתנדנדות rheometry בדיקות באמצעות rheometer מסחרי וכדי להפעיל ניתוח SPP freeware כדי לפרש ולהבין את התגובות מתח לא לינארית של שתי תמיסות פולימר ברורים. המסגרת SPP, אשר בעבר הוכח לתאם עם שינויים מבניים וכדי להקל על ההבנות של מערכות colloidal רבים, ניתן להחיל באופן שווה למער...

Access restricted. Please log in or start a trial to view this content.

Disclosures

המחברים אין לחשוף.

Acknowledgements

המחברים מודים פאר אנטון על השימוש rheometer 702 בתפוז דרך תוכנית המחקר האקדמי שלהם VIP. אנו מודים גם ד ר אייל שטי על ההערות בכיוונון כלי נגינה.

Access restricted. Please log in or start a trial to view this content.

Materials

NameCompanyCatalog NumberComments
SPP analysis softwareSimon Rogers Group (UIUC)SPPplus_v1p1Attached as supplementary files
MATLABMathwork
RheometerAnton PaarMCR 702 TwinDrive
50mm 2-degree coneAnton PaarCP50-2Upper measuring system
50mm plateAnton PaarPP50Lower measuring system
Xanthan gum (XG)Sigma-Aldrich11138-66-2
Polyethylene oxide (PEO)Sigma-Aldrich25322-68-3Mv=1,000,000
Dimethyl sulfoxide (DMSO)Sigma-Aldrich67-68-5

References

  1. Dolz, M., Hernández, M. J., Delegido, J., Alfaro, M. C., Muñoz, J. Influence of xanthan gum and locust bean gum upon flow and thixotropic behaviour of food emulsions containing modified starch. Journal of Food Engineering. 81 (1), 179-186 (2007).
  2. Gupta, N., Zeltmann, S. E., Shunmugasamy, V. C., Pinisetty, D. Applications of Polymer Matrix Syntactic Foams. JOM. 66 (2), 245-254 (2013).
  3. Garcıa-Ochoa, F., Santos, V. E., Casas, J. A., Gómez, E. Xanthan gum: production, recovery, and properties. Biotechnology Advances. 18 (7), 549-579 (2000).
  4. Chang, I., Im, J., Prasidhi, A. K., Cho, G. -C. Effects of Xanthan gum biopolymer on soil strengthening. Construction and Building Materials. 74, 65-72 (2015).
  5. Rogers, S. A. In search of physical meaning: defining transient parameters for nonlinear viscoelasticity. Rheologica Acta. 56 (5), 501-525 (2017).
  6. Ferry, J. D. Viscoelastic properties of polymers. , John Wiley & Sons. (1980).
  7. Bird, R. B., Armstrong, R. C., Hassager, O. Dynamics of Polymeric Liquids. Volume 1: Fluid Mechanics. , John Wiley & Sons. New York. (1987).
  8. Park, J. D., Rogers, S. A. The transient behavior of soft glassy materials far from equilibrium. Journal of Rheology. 62 (4), 869-888 (2018).
  9. Rogers, S., Kohlbrecher, J., Lettinga, M. P. The molecular origin of stress generation in worm-like micelles, using a rheo-SANS LAOS approach. Soft Matter. 8 (30), 7831-7839 (2012).
  10. Lettinga, M. P., Holmqvist, P., Ballesta, P., Rogers, S., Kleshchanok, D., Struth, B. Nonlinear Behavior of Nematic Platelet Dispersions in Shear Flow. Phys Rev Lett. 109 (24), 246001(2012).
  11. Hyun, K., Wilhelm, M., et al. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Progress in Polymer Science. 36 (12), 1697-1753 (2011).
  12. Park, J. D., Ahn, K. H., Lee, S. J. Structural change and dynamics of colloidal gels under oscillatory shear flow. Soft Matter. 11 (48), 9262-9272 (2015).
  13. Lee, C. -W., Rogers, S. A. A sequence of physical processes quantified in LAOS by continuous local measures. Korea-Australia Rheology Journal. 29 (4), 269-279 (2017).
  14. Rogers, S. A., Erwin, B. M., Vlassopoulos, D., Cloitre, M. A sequence of physical processes determined and quantified in LAOS: Application to a yield stress fluid. Journal of Rheology. 55 (2), 435-458 (2011).
  15. Wagner, M. H., Rolon-Garrido, V. H., Hyun, K., Wilhelm, M. Analysis of medium amplitude oscillatory shear data of entangled linear and model comb polymers. Journal of Rheology. 55 (3), 495-516 (2011).
  16. Radhakrishnan, R., Fielding, S. Shear banding in large amplitude oscillatory shear (LAOStrain and LAOStress) of soft glassy materials. Journal of Rheology. 62 (2), 559-576 (2018).
  17. Bharadwaj, N. A., Ewoldt, R. H. Constitutive model fingerprints in medium-amplitude oscillatory shear. Journal of Rheology. 59 (2), 557-592 (2015).
  18. Wilhelm, M. Fourier‐Transform Rheology. Macromolecular Materials and Engineering. 287 (2), 83-105 (2002).
  19. Ewoldt, R. H., Hosoi, A. E., McKinley, G. H. New measures for characterizing nonlinear viscoelasticity in large amplitude oscillatory shear. Journal of Rheology. 52 (6), 1427-1458 (2008).
  20. Rogers, S. A., Lettinga, M. P. A sequence of physical processes determined and quantified in large-amplitude oscillatory shear (LAOS): Application to theoretical nonlinear models. Journal of Rheology. 56 (1), 1-25 (2011).
  21. Rogers, S. A. A sequence of physical processes determined and quantified in LAOS: An instantaneous local 2D/3D approach. Journal of Rheology. 56 (5), 1129-1151 (2012).
  22. Kim, J., Merger, D., Wilhelm, M., Helgeson, M. E. Microstructure and nonlinear signatures of yielding in a heterogeneous colloidal gel under large amplitude oscillatory shear. Journal of Rheology. 58 (5), 1359-1390 (2014).
  23. van der Vaart, K., Rahmani, Y., Zargar, R., Hu, Z., Bonn, D., Schall, P. Rheology of concentrated soft and hard-sphere suspensions. Journal of Rheology. 57 (4), 1195-1209 (2013).
  24. Poulos, A. S., Stellbrink, J., Petekidis, G. Flow of concentrated solutions of starlike micelles under large-amplitude oscillatory shear. Rheologica Acta. 52 (8-9), 785-800 (2013).
  25. Armstrong, M. J., Beris, A. N., Rogers, S. A., Wagner, N. J. Dynamic shear rheology of a thixotropic suspension: Comparison of an improved structure-based model with large amplitude oscillatory shear experiments. Journal of Rheology. 60 (3), 433-450 (2016).
  26. Calabrese, M. A., Wagner, N. J., Rogers, S. A. An optimized protocol for the analysis of time-resolved elastic scattering experiments. Soft Matter. 12 (8), 2301-2308 (2016).

Access restricted. Please log in or start a trial to view this content.

Reprints and Permissions

Request permission to reuse the text or figures of this JoVE article

Request Permission

Explore More Articles

146Rheologyviscoelasticviscoplastic

This article has been published

Video Coming Soon

JoVE Logo

Privacy

Terms of Use

Policies

Contact Us

Recommend to library

JoVE NEWSLETTERS

Research

Education

Authors

Librarians

ABOUT JoVE

Copyright © 2025 MyJoVE Corporation. All rights reserved