基于结构的转录因子蛋白沿DNA从原子级步进到粗晶扩散运动的模拟和采样

摘要

该协议的目标是揭示蛋白质沿DNA的一维扩散的结构动力学，使用植物转录因子WRKY结构域蛋白作为示例系统。为此，已经实施了原子和粗粒度分子动力学模拟以及广泛的计算采样。

摘要

转录因子（TF）蛋白沿DNA的一维（1-D）滑动对于促进TF的扩散以定位遗传调控的靶DNA位点至关重要。检测TF滑动或踩踏DNA的碱基对（bp）分辨率在实验上仍然具有挑战性。我们最近进行了全原子分子动力学（MD）模拟，捕获了小的WRKY结构域TF蛋白沿DNA的自发1-bp步进。基于从此类仿真中获得的10 μs WRKY步进路径，此处的协议显示了如何通过构建用于1-bp蛋白质步进的马尔可夫状态模型（MSM）对TF-DNA系统进行更广泛的构象采样，并测试各种数量的微观和宏观状态用于MSM构建。为了检查TF蛋白与结构基础的DNA的加工一维扩散搜索，该方案进一步展示了如何进行粗粒度（CG）MD模拟以采样系统的长期尺度动力学。与全原子模拟揭示的亚微秒到微秒的蛋白质步进运动相比，这种CG建模和模拟对于揭示蛋白质-DNA静电对TF蛋白质在几十微秒以上的过程扩散运动的影响特别有用。

引言

转录因子（TF）寻找靶DNA以结合和调节基因转录及相关活性¹.除了三维（3D）扩散之外，TF的促进扩散被认为是靶DNA搜索所必需的，其中蛋白质还可以沿着一维（1D）DNA滑动或跳跃，或者在DNA^2，3，⁴，^5，6，7上进行节间转移。

在最近的一项研究中，我们对植物TF进行了数十微秒（μs）全原子平衡分子动力学（MD）模拟 - DNA⁸上的WRKY结构域蛋白。在微秒内捕获了WRKY在多晶A DNA上的完整1-bp步进。已经观察到蛋白质沿DNA槽的运动和氢键（HBs）断裂重整动力学。虽然这样的轨迹代表了一条采样路径，但整体蛋白质步进景观仍然缺乏。在这里，我们展示了如何使用构建的马尔可夫状态模型（MSM）围绕最初捕获的蛋白质步进路径扩展计算采样，该模型已广泛实施，用于模拟涉及实质性构象变化和时间尺度分离的各种生物分子系统^{9，10，11，12，13，14，15，16，17，18，19}.目的是揭示TF蛋白沿DNA扩散的构象集合和亚稳态，用于一个循环步骤。

虽然上述MD模拟揭示了DNA上1 bp的蛋白质运动的原子分辨率，但TF以相同的高分辨率沿DNA的长期过程扩散的结构动力学几乎不容易获得。然而，在残留物水平上进行粗粒度（CG）MD仿真在技术上是可行的。CG模拟时间尺度可以有效地扩展到比原子模拟长^{20、21、22、23、24、25、26、}27^、28、29的几十倍或几百倍。在这里，我们展示了通过实施Takada lab³⁰开发的CafeMol软件进行的CG模拟。

在目前的方案中，我们首先介绍了沿多A DNA和MSM构建的WRKY结构域蛋白的原子模拟，其重点是对沿DNA仅1 bp的蛋白质步进运动进行采样。然后，我们提出了同一蛋白质 - DNA系统的CG建模和模拟，该系统将计算采样扩展到蛋白质沿着DNA的数十个bps上的过程扩散。

在这里，我们使用GROMACS^31，32，33 软件进行MD模拟，并使用MSMbuilder³⁴ 构建用于采样构象快照的MSM，以及使用VMD³⁵ 可视化生物分子。该协议要求用户能够安装和实现上述软件。然后，CafeMol³⁰ 软件的安装和实施对于进行CG MD模拟是必要的。在VMD中还对轨迹和可视化进行了进一步的分析。

研究方案

1. 从原子MD模拟构建马尔可夫状态模型（MSM）

1. 自发蛋白质步进途径和初始结构收集
   1. 使用先前获得的10μs全原子MD轨迹⁸ 从"向前"的1-bp步进路径（即，每纳秒一帧）中均匀地提取10000帧。帧的总数需要足够大，以包括所有代表性构象。
   2. 在 VMD 中准备具有 10000 帧的过渡路径，方法是单击 "文件">"保存坐标"，在"所选原子"框中键入蛋白质或细胞核，然后在"帧"框中选择帧，单击" 保存 "以获取所需的帧。
      注意:先前获得的10 μs全原子MD模拟轨迹（此处称为"正向步进轨迹"），用于在34 bp均相多晶A DNA⁸上进行WRKY步进1-bp距离，用作启动进一步构象采样的初始路径。然而，请注意，在大多数实践中，通过执行定向或有针对性的MD模拟，或实现一般的路径生成方法等，可以构造初始^路径。
   3. 将参考DNA的长轴（从晶体结构）对齐到x轴，并将完整的34-bp DNA的初始质心（COM）设置在坐标空间的原点，以方便进一步数据分析。为此，请单击 VMD 中 Tk 控制台>扩展 ，然后在 Tk 控制台命令窗口中键入:
      源旋转.tcl
      tcl 脚本可以在 补充文件 3 中找到。
   4. 然后通过将中心10 bp DNA（A 14至23和T 14'至23'）与晶体结构⁴⁰的DNA对齐来计算蛋白质主链的均方根距离（RMSD），RMSD表示系统的几何测量值（见 图1A）。为此，请单击 "VMD >扩展>分析> RMSD 轨迹工具 ，然后在原子选择框中键入核和残基 14 到 23 和 46 到 55，单击 对齐 ，然后单击 RMSD 框以计算 RMSD 值。
   5. 在 MATLAB 中，通过键入命令，计算蛋白质围绕 y-z 平面上 DNA Θ（t） 的旋转度
      rad2deg（atan（z/y））
      初始角度定位定义为 Θ（0）=0，如之前执行的⁸ 所示。
   6. 在 MATLAB⁴¹ 中键入以下命令以使用 K-means 方法^42，43，44 ，并通过键入将 10000 个结构分类为 25 个聚类:
      [idx， C]=kmeans（ X， 25）
      这里的 X 是RMSD的2D矩阵和WRKY在DNA上的旋转角度。收集这 25 个集群中心的结构，以进行进一步的 MD 模拟。
      注意:由于相对于DNA采样的蛋白质RMSD覆盖约25 Å的范围，因此我们选择25个簇以每埃具有一个簇。
2. 进行^第一 轮MD模拟和模拟设置
   1. 在 parmbsc1 力场⁴⁵ 下使用 GROMACS 5.1.2 软件³² 并使用 shell 中补充文件 2 中的 buildsystem.sh 文件，为 25 个结构构建原子系统。
   2. 通过在shell中键入以下命令，在NPT集成下对这25个系统进行60-ns MD仿真，时间步长为2 fs:
      gmx_mpi grompp -f md.mdp -c npt.gro -p topol.top -o md.tpr
      gmx_mpi mdrun -deffnm md
3. 聚类 1^圣 圆形 MD 轨迹
   1. 通过在 shell 中键入来删除每个仿真轨迹的前 10 ns:
      gmx_mpi trjcat -f md.xtc -b 10000 -e 600000 -o newtraj.xtc
      并从 25 × 50 ns 轨迹中收集构象以进行聚类，以便为后续更广泛的采样（^第 2 轮 MD 模拟）准备输入结构。
      注意:为了减少初始路径的影响并允许局部平衡，删除了10-ns的初始仿真周期。
   2. 选择蛋白质和DNA之间的距离对作为时间无关成分分析（tICA）^46，47，48 投影的输入参数。使用GROMACS中的 make_ndx 命令来执行此操作:
      gmx_mpi make_ndx -f 输入.pdb -o index.ndx
      注意:这里，选择了残基Y119，K122，K125，R131，Y133，Q146，K144，R135，W116，R117，Y134，K118，Q121的蛋白质CA原子和重原子（NH1，NH2，OH，NZ，NE2，ND2），它们可以与DNA核苷酸形成氢键（HBs），它们与DNA核苷酸的O1P O2P和N6原子配对（A14-20， T19-23）。选定的氨基酸可以形成稳定的HBs或与DNA的盐桥。
   3. 将上述选定的原子索引从 index.ndx 文件复制到新的文本文件（索引.dat）。通过 python 脚本从 补充文件 1 中获取这些原子之间的对信息，generate_atom_indices.py并键入:
      python2.6 generate_atom_indices.py索引.dat >原子索引.txt
      这在蛋白质和DNA之间生成415个距离对。
   4. 通过在 MSMbuilder 命令窗口中键入以下命令，计算每个轨迹的 415 个距离对:
      msmb AtomPairsFeaturizer -out pair_features --pair_indices AtomIndices.txt --top references.pdb --trjs "trajectories/*.xtc" --transformed pair_features --stride 5
   5. 执行 tICA，通过键入以下内容，将数据维度减小到前 2 个与时间无关的分量 （tIC） 或向量上:
      msmb tICA -i ../tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --伽马 0.05 -t tica_results.h5
      注意:tICA是一种降维方法，它计算时间滞后相关矩阵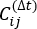 的特征值，通过以下公式确定仿真系统最慢的松弛自由度: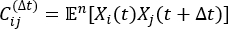
      
      其中 X_i（t） 是时间 t 处第 i 个反应坐标的值，X_j（t+Δt） 是时间 t+Δt 时第 j 个反应坐标的值。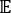是 X_i（t） 和 X _j（t + Δ t） 整体仿真轨迹的乘积的期望值。沿最慢松弛自由度的方向对应于上述时间滞后相关矩阵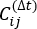的最大特征值。在这里，2个tIC似乎是在我们的MSM构造上区分三个宏观状态的最小集合（稍后讨论）。例如，还可以计算广义矩阵瑞利商（GMRQ）得分⁴⁹，以探索要使用的最佳分量集。
   6. 使用 MSMbuilder 中的命令，通过 K-center^{43，44 方法将}投影数据集聚类到 100 个聚类中（参见图 1B）:
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 100.
      选择每个聚类的中心结构作为^第 二轮 MD 模拟的初始结构。维护模拟的100个结构的模拟信息，包括位置、温度、压力等，速度除外。
      注意:在第一轮25次模拟之后，初始路径的内存已经减少，因此我们在第二轮中生成了更多的聚类，例如100个聚类，以大幅扩展构象采样。
4. 进行^第 二轮广泛的MD模拟
   1. 从这100个初始结构开始，在所有原子上施加随机初始速度后，进行60-ns MD仿真。通过在 mdp 文件中打开速度生成来添加随机初始速度，即将 md.mdp 文件gen_vel = 否 更改为 gen_vel = yes。
   2. 按照步骤 1.3.1 中所述，删除每个仿真的前 10 个 ns，从 100 个× 50 ns 轨迹中平均收集 2，500，000 个快照以构建 MSM。
      注意:请注意，在后来的宏观状态构造中，发现了少量具有特别低总体（X-Θ平面底部约0.2%）的偏离路径状态。当宏态的总数设置为 3 到 6 时，这些偏离路径状态被分类为一个宏状态（图 2B）。由于如此低的总体宏观状态仅包括3个轨迹，这些轨迹最终被移除，因此该协议中显示的结果确实是从97×50 ns轨迹中获得的，总共有2，425，000帧或快照。
5. 聚类^第 2 轮 MD 轨迹
   1. 像以前一样，对^第 2轮轨迹进行tICA。在 MSMbuilder 中键入:
      msmb tICA -i ../tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --伽马 0.05 -t tica_results.h5
   2. 计算隐含的时间尺度，以验证相关延迟时间Δt和微观状态数的参数（见 图1C），
      
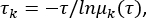
      其中 τ 表示用于构建转移概率矩阵 （TPM） 的滞后时间;μ_k（τ） 表示滞后时间 τ 下 TPM 的第 k 个特征值。将 补充文件 1 中的 python 脚本用于此 python BuildMSMsAsVaryLagTime.py -d .。/ -f ../trajlist_num -i 50 -m 1000 -t 10 -n 20 -s 500.
   3. 通过更改上面使用的参数来改变滞后时间 τ 和微状态数:
      python BuildMSMsAsVaryLagTime.py -d ../ -f ../trajlist_num -i 50 -m 1000 -t 5 10 20 30 40 -n 20 -s 20 200 400 500 800 2000
      注意:当隐含的时间尺度曲线开始随着时间尺度分离而趋于平稳时，系统被视为马尔可夫系统。然后，选择 Dt 作为相关延迟时间，选择 τ 作为隐含时间刻度开始趋于平稳以构建 MSM 的延迟时间。
   4. 因此，选择一个相对较大（但不太大）的状态数，N = 500，以及相对较短的相关延迟时间Δt = 10 ns。发现构建 MSM 的滞后时间为 τ =10 ns。
   5. 使用以下命令将构象分类为 500 个簇（参见 图 1D）:
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 500
6. 中微管理建筑
   1. 将 500 个微观状态集中为 3–6 个宏观状态，以找出最适合根据 MSMbuilder 中的 PCCA+ 算法⁵⁰ 的宏观状态的数量，方法是使用补充文件 1 python msm_lumping_usingPCCAplus.py中的 python 脚本。通过构建少量的宏观状态，即在动力学上聚集数百个微观状态，如下^所述，确定生物分子最基本的构象变化的模型的简化动力学^网络。
   2. 如步骤1.1.3和1.1.4所述，将高维构象映射到X（蛋白质沿DNA长轴的运动）和蛋白质沿DNA的旋转角度（例如，没有状态具有过低的种群<1%;见 图2C）。然后找到最能代表系统的3个宏状态（图1E）。参见 图2D ，了解蛋白质沿DNA的运动和蛋白质围绕DNA的旋转角度的快照。
      注意:在之前生成10 μs自发蛋白质正向步进路径的工作中，我们还进行了5 x 4 μs平衡MD模拟，以适度扩展采样。我们显示了原始正向路径的映射（见 图2A 左图）以及先前进行的正向路径上进一步的4μs采样轨迹（见 图2A 右）⁸。图中显示了本工作中使用的原始100×50 ns（见 图2B 左）⁸ 和97×50 ns轨迹的映射（见 右图2B ）。
7. 计算平均首次通过时间 （MFPT）
   1. 根据 500 微状态 MSM 的 TPM 执行五个 10 ms 蒙特卡罗 （MC） 轨迹，并将 10 ns 的延迟时间设置为 MC 的时间步长。通过补充文件 1 python python mfpt_msm3.py中的 python 脚本计算每对宏状态之间的 MFPT⁵²（图 3）。
   2. 使用 补充文件 2 中的 bash 文件计算 MFPT 的平均误差和标准误差，键入:
      sh mfpt_analysis.bash

2. 进行粗粒度（CG）模拟，对长时间动力学进行采样

1. 使用CafeMol 3.0^软件30进行CG模拟。查看在扩展名为 .inp 的输入配置文件中指定的 CG 模拟设置，包括输入结构、模拟参数、输出文件等。在终端上键入以下命令以运行 CG 模拟:
   咖啡酚 XXX.inp
2. 在输入文件中指定以下块，每个块都以标签 < and ending with >>>>开头。
   1. 设置文件名块（必需）以指定工作目录和输入/输出文件存储路径。为这些模拟的文件名块键入以下内容:
      <<<<文件名
      路径 = XXXXX（工作路径）
      文件名 = wrky（输出文件名）
      输出 psf pdb 电影 dcd rst
      path_pdb = XXXXX（输入本机结构路径）
      path_ini = XXXXX（输入初始结构路径）
      path_natinfo = XXXXX（本机信息文件路径）
      path_para = XXXXX（参数文件路径）
      >>>>
      注意:由于Go-model⁵³ 在CG建模中使用，即蛋白质将偏向于天然构象，因此需要将建模结构设置为天然构象。在这里，输入晶体结构被设置为原生构象。
   2. 设置作业控制块（必需）以定义模拟的运行模式。键入以下命令:
      <<<< job_cntl
      i_run_mode = 2（= 2 恒温模拟）
      i_simulate_type = 1 （=1 朗格文动力学）
      i_initial_state = 2（=2 表示初始配置为本机配置）
      >>>>
      选择恒温朗格文动力学仿真。
   3. 设置单位和状态块（必需）以定义输入结构的信息。键入以下命令:
      <<<< unit_and_state
      i_seq_read_style = 1（=1 表示从 PDB 文件读取序列）
      i_go_native_read_style = 1（=1 表示本机结构来自 PDB 文件）
      1蛋白质蛋白质.pdb（单位和状态molecular_type native_structure）
      2-3 DNA DNA.pdb（单位和状态molecular_type native_structure）
      >>>>
      注意:需要初始输入结构文件（蛋白质.pdb和DNA.pdb此处）。这些结构以 pdb 格式编写。这里需要两个pdb文件:一个是包含WRKY重原子坐标（单元1）的蛋白质结构文件，另一个是200-bp双链（ds）DNA（单元2-3）的坐标。蛋白质最初放置在距离DNA15埃的位置。
   4. 设置energy_function块中定义的能量功能块（必需）。键入以下命令:
      <<<< energy_function
      本地（1） L_GO
      本地（2-3） L_DNA2
      NLOCAL（1/1） GO EXV ELE
      NLOCAL（2-3/2-3） ELE DNA
      NLOCAL（1/2-3） EXV ELE
      i_use_atom_protein = 0
      i_use_atom_dna = 0
      i_para_from_ninfo = 1
      i_triple_angle_term = 2
      >>>>
      注意:在CG模拟中，蛋白质由Go-model⁵³ 粗粒度表示，每个氨基酸由放置在其Cα位置的CG颗粒表示。蛋白质构象将在Go电位下偏向天然结构或晶体结构（图4A 左）。DNA由3SPN.2模型⁵⁴描述，其中每个核苷酸由3个CG颗粒S，P，N表示，分别对应于糖，磷酸盐和含氮碱基（图4A 右）。考虑不同链之间的静电和vdW相互作用。在CG模拟中，蛋白质和DNA之间的静电相互作用近似于Debye-Hückel电位⁵⁵。vdW斥力能量采用与围棋模型中相同的形式。
   5. 设置md_information块（必需）以定义仿真信息。键入以下命令:
      <<<< md_information
      n_step_sim = 1
      n_tstep（1） = 500000000
      tstep_size = 0.1
      n_step_save = 1000
      n_step_neighbor = 100
      i_com_zeroing = 0
      i_no_trans_rot = 0
      温度 = 300.0
      n_seed = -1
      >>>>
      n_tstep是模拟步骤。将tstep_size设置为每个MD步骤的时间长度，每个CG Cafemol时间步骤约为200 fs³⁰，因此这里的每个MD步骤原则上为200×0.1 fs。每 100 MD 步更新一次邻居列表（n_step_neighbor = 100）。将模拟温度设置为300 K.通过使用Berendsen恒温器⁵⁶更新蛋白质结构的速度型Verlet算法来控制温度。
      注意:n_step_sim是基于Go模型势的盆地数，或能量曲线的局部最小数。多盆电位允许蛋白质构象偏向于不同的构象，以便蛋白质构象可以从一个局部最小值变化到另一个局部最小值。这里只使用单个盆地Go模型，这意味着在模拟中蛋白质只有一个偏置构象（晶体结构）。同时，由于在CG背景下没有蛋白质 - DNA氢键相互作用等，因此分子运动的采样速度甚至更快，即比原子模拟中的>10倍。
   6. 设置静电块（仅在使用静电相互作用时才需要）作为不同链之间的静电相互作用的考虑因素，因此使用此块通过键入来定义静电相互作用的参数:
      <<<<静电
      cutoff_ele = 10.0
      ionic_strength = 0.15
      >>>>
      将静电相互作用中的 Debye 长度设置为 10 Å，对应于溶液条件。将离子强度设置为0.15 M，如生理状况一样。

结果

旋转耦合滑动或 1 bp 步进的 WRKY 从 MSM 结构
DNA上的所有蛋白质构象都映射到蛋白质COM沿DNA的纵向运动X和旋转角度（见 图3A）。这两个度的线性偶联表示WRKY结构域蛋白在DNA上的旋转耦合步进。构象可以在 MSM 中进一步聚类为 3 个宏状态（S1、S2 和 S3）。然后，WRKY 的正向步进遵循宏观状态转换 S1->S2->S3。S1是指由建模结构（基于WRKY-DNA复合物⁴⁰的?...

讨论

这项工作解决了如何进行基于结构的计算模拟和采样，以揭示转录因子或TF蛋白沿着DNA移动，不仅在步进的原子细节下，而且在过程扩散中，这对于TF在DNA靶标搜索中的促进扩散至关重要。为此，首先构建了小TF结构域蛋白WRKY沿着均匀的poly-A DNA步进1-bp的马尔可夫状态模型或MSM，以便可以揭示DNA上的蛋白质构象集合以及蛋白质 - DNA界面处的集体氢键或HB动力学。为了获得MSM，我们沿着自发蛋白质步?...

材料

Name	Company	Catalog Number	Comments
CafeMol	Kyoto University		coarse-grained (CG) simulations
GROMACS	University of Groningen Royal Institute of Technology Uppsala University		molecular dynamics simulations software
Matlab	MathWorks		Numerical calculation software
MSMbuilder	Stanford University		build MSM
VMD	UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN		molecular visualization program