JoVE Logo
Yazarlar
Bize Ulaşın

Oturum Aç

Bu içeriği görüntülemek için JoVE aboneliği gereklidir. Oturum açın veya ücretsiz deneme sürümünü başlatın.

Bu Makalede

  • Özet
  • Özet
  • Giriş
  • Protokol
  • Sonuçlar
  • Tartışmalar
  • Açıklamalar
  • Teşekkürler
  • Malzemeler
  • Referanslar
  • Yeniden Basımlar ve İzinler

Özet

Bu protokolün amacı, örnek bir sistem olarak bir bitki transkripsiyon faktörü WRKY alan proteini kullanarak, DNA boyunca proteinin tek boyutlu difüzyonunun yapısal dinamiklerini ortaya çıkarmaktır. Bunu yapmak için, hem atomistik hem de kaba taneli moleküler dinamik simülasyonları ve kapsamlı hesaplamalı örneklemeler uygulanmıştır.

Özet

Transkripsiyon faktörü (TF) proteininin DNA boyunca tek boyutlu (1-D) kayması, genetik düzenleme için hedef DNA bölgesini bulmak için TF'nin difüzyonunun kolaylaştırılması için gereklidir. TF'nin DNA'ya kayması veya basması baz çifti (bp) çözünürlüğünü tespit etmek hala deneysel olarak zordur. Son zamanlarda, DNA boyunca küçük bir WRKY alan TF proteininin kendiliğinden 1-bp adımını yakalayan tüm atom moleküler dinamiği (MD) simülasyonlarını gerçekleştirdik. Bu tür simülasyonlardan elde edilen 10 μs WRKY adım yoluna dayanarak, buradaki protokol, 1-bp protein basamağı için Markov durum modelini (MSM) oluşturarak, MSM yapısı için test edilen çeşitli mikro ve makro durumlarla TF-DNA sistemlerinin daha kapsamlı konformasyonel örneklemelerinin nasıl yapılacağını göstermektedir. TF proteininin DNA ile birlikte yapısal temeldeki işlemsel 1-D difüzyonel aramasını incelemek için, protokol ayrıca sistemin uzun süreli ölçek dinamiklerini örneklemek için kaba taneli (CG) MD simülasyonlarının nasıl yapılacağını göstermektedir. Bu tür CG modellemesi ve simülasyonları, TF proteininin onlarca mikrosaniyenin üzerindeki işlemsel difüzyonel hareketleri üzerindeki protein-DNA elektrostatik etkilerini, tüm atom simülasyonlarından ortaya çıkarılan mikrosaniyeler ila mikrosaniyeler arasındaki protein adım atma hareketleriyle karşılaştırıldığında ortaya çıkarmak için özellikle yararlıdır.

Giriş

Transkripsiyon faktörleri (TF), gen transkripsiyonunu ve ilgili aktiviteleri bağlamak ve düzenlemek için hedef DNA'yıarar 1. Üç boyutlu (3D) difüzyonun yanı sıra, TF'nin kolaylaştırılmış difüzyonunun, proteinlerin tek boyutlu (1D) DNA boyunca kayabileceği veya zıplayabileceği veya DNA 2,3,4,5,6,7 üzerinde segmentler arası transfer ile atlayabileceği hedef DNA araştırması için gerekli olduğu öne sürülmüştür.

Son zamanlarda yapılan bir çalışmada, bir bitki TF - DNA8 üzerindeki WRKY alan proteini - üzerinde onlarca mikrosaniye (μs) tüm atom dengesi moleküler dinamiği (MD) simülasyonu gerçekleştirdik. Mikrosaniyeler içinde poli-A DNA'sı üzerinde WRKY'nin tam 1-bp basamağı yakalandı. Proteinin DNA oluğu boyunca hareketleri ve hidrojen bağları (HBs) kırılma-reform dinamikleri gözlenmiştir. Böyle bir yörünge örneklenmiş bir yolu temsil ederken, genel bir protein basamaklama manzarası hala eksiktir. Burada, önemli konformasyonel değişiklikler ve zaman ölçeği ayrımı içeren çeşitli biyomoleküler sistemleri simüle etmek için yaygın olarak uygulanan yapılandırılmış Markov durum modeli (MSM) ile başlangıçta yakalanan protein basamak yolu etrafındaki hesaplamalı örneklemelerin nasıl genişletileceğini gösteriyoruz 9,10,11,12,13,14,15,16, 17,18,19. Amaç, bir siklik adım için DNA boyunca TF protein difüzyonunun konformasyonel topluluk ve meta-kararlı durumlarını ortaya çıkarmaktır.

Yukarıdaki MD simülasyonu, DNA üzerindeki 1 bp için protein hareketlerinin atomik çözünürlüğünü ortaya çıkarırken, TF'nin DNA boyunca aynı yüksek çözünürlükte uzun süreli işlemsel difüzyonunun yapısal dinamiklerine pek erişilemez. Bununla birlikte, kalıntı düzeyinde kaba taneli (CG) MD simülasyonlarının yapılması teknik olarak ulaşılabilirdir. CG simülasyon zaman ölçeği, atomik simülasyonlardan 20,21,22,23,24,25,26,27,28,29'dan onlarca veya yüzlerce kat daha uzun bir süreye kadar etkili bir şekilde genişletilebilir. Burada, Takada lab30 tarafından geliştirilen CafeMol yazılımı uygulanarak yapılan CG simülasyonlarını gösteriyoruz.

Mevcut protokolde, WRKY alan proteininin poli-A DNA boyunca atomik simülasyonlarını ve önce DNA boyunca sadece 1 bp için protein adım hareketlerini örneklemeye odaklanan MSM yapısını sunuyoruz. Daha sonra, hesaplamalı örneklemeyi DNA boyunca onlarca bps boyunca protein prosesi difüzyonuna genişleten aynı protein-DNA sisteminin CG modellemesini ve simülasyonlarını sunuyoruz.

Burada, MD simülasyonları yapmak için GROMACS 31,32,33 yazılımını ve örneklenmiş konformasyonel anlık görüntüler için MSM'yi oluşturmak için MSMbuilder34'ü ve biyomolekülleri görselleştirmek için VMD35'i kullanıyoruz. Protokol, kullanıcının yukarıdaki yazılımı yükleyebilmesini ve uygulayabilmesini gerektirir. CG MD simülasyonlarını yürütmek için CafeMol30 yazılımının kurulumu ve uygulanması daha sonra gereklidir. VMD'de yörüngelerin ve görselleştirmenin daha ileri analizleri de yapılmaktadır.

Protokol

1. Atomik MD simülasyonlarından Markov durum modelinin (MSM) yapımı

  1. Spontan protein basamak yolu ve başlangıç yapılarının toplanması
    1. "İleri" 1-bp basamak yolundan (yani, her nanosaniye için bir kare) 10000 kareyi eşit olarak çıkarmak için daha önce elde edilen 10-μs tüm atomlu MD yörünge8'i kullanın. Toplam çerçeve sayısının, tüm temsili konformasyonları içerecek kadar büyük olması gerekir.
    2. VMD'de Dosya > Koordinatları kaydet'e tıklayarak geçiş yolunu hazırlayın, seçili atomlar kutusuna protein veya nükleik yazın ve Çerçeveler kutusunda çerçeveleri seçin, gerekli kareleri almak için Kaydet'i tıklatın.
      NOT: 34-bp homojen poli-A DNA8 üzerinde WRKY adım 1-bp mesafesi için daha önce elde edilen 10 μs tüm atomlu MD simülasyon yörüngesi (burada "ileri adım yörüngesi" olarak adlandırılır), daha fazla konformasyonel örnekleme başlatmak için ilk yol olarak kullanılmıştır. Bununla birlikte, uygulamaların çoğunda, yönlendirilmiş veya hedeflenmiş MD simülasyonları gerçekleştirilerek veya genel yol oluşturma yöntemleri uygulanarak bir başlangıç yolunun oluşturulduğunu unutmayın.36,37,38,39.
    3. Referans DNA'nın uzun eksenini (kristal yapıdan) x eksenine hizalayın ve daha fazla veri analizinin rahatlığı için koordinat uzayının kökeninde tam 34-bp DNA'nın başlangıç kütle merkezini (COM) ayarlayın. Bunu yapmak için, VMD'de Tk Konsolu> Uzantılar'a tıklayın ve Tk konsolu komut penceresine yazın:
      kaynak rotate.tcl
      tcl komut dosyası Ek Dosya 3'te bulunabilir.
    4. Ardından, merkezi 10 bp DNA'sını (A 14 ila 23 ve T 14' ila 23') kristal yapı40'tan buna hizalayarak protein omurgasının kök-ortalama-kare mesafesini (RMSD) hesaplayın ve RMSD, sistemlerin geometrik ölçümlerini temsil eder (bkz. Şekil 1A). Bunu, RMSD yörünge aracında VMD > Uzantıları > Analizi>ni tıklatarak yapın ve atom seçim kutusuna çekirdek ve kalıntı 14 - 23 ve 46 - 55 yazın, RMSD değerlerini hesaplamak için Hizala'yı ve ardından RMSD kutusunu tıklatın.
    5. MATLAB'da y-z düzleminde DNA Θ(t) etrafındaki proteinin dönme derecesini komutu yazarak hesaplayın
      rad2deg(atan(z/y))
      ilk açısal konumlandırma daha önce8'de yapıldığı gibi Θ(0)=0 olarak tanımlanır.
    6. K-means yöntemleri42,43,44'ü kullanmak için MATLAB41'e aşağıdaki komutu yazın ve 10000 yapılarını yazarak 25 küme halinde sınıflandırın:
      [idx, C]=kmeans( X, 25)
      Burada X , RMSD'nin 2B matrisi ve DNA üzerindeki WRKY'nin dönme açısıdır. Daha fazla MD simülasyonu için bu 25 küme merkezinin yapılarını toplayın.
      NOT: DNA'ya göre örneklenen RMSD proteini yaklaşık 25 Å'lik bir aralığı kapsadığından, angstrom başına bir kümeye sahip olmak için 25 küme seçiyoruz.
  2. MD simülasyonlarının 1. turunun ve simülasyon ayarlarının yapılması
    1. Parmbsc1 kuvvet alanı 45 altında GROMACS 5.1.2 yazılımı32'yi kullanarak ve kabuktaki Ek Dosya 2'deki buildsystem.sh dosyasını kullanarak25 yapı için atomistik sistemler oluşturun.
    2. NPT topluluğu altındaki bu 25 sistem için 60-ns MD simülasyonlarını, kabukta aşağıdaki komutu yazarak 2 fs'lik bir zaman adımıyla gerçekleştirin:
      gmx_mpi grompp -f md.mdp -c npt.gro -p topol.top -o md.tpr
      gmx_mpi mdrun -deffnm md
  3. 1'i kümelemesokak yuvarlak MD yörüngeleri
    1. Kabuk yazarak her simülasyon yörüngesinin ilk 10 n'sini kaldırın:
      gmx_mpi trjcat -f md.xtc -b 10000 -e 600000 -o newtraj.xtc
      ve sonraki daha kapsamlı örneklemeler (2. tur MD simülasyonları) için giriş yapılarını hazırlamak üzere kümeleme için 25 × 50 ns yörüngelerinden konformasyonlar toplayın.
      NOT: İlk yoldan gelen etkiyi azaltmak ve yerel dengeye izin vermek için, simülasyonların ilk periyodunun 10-n'si kaldırıldı.
    2. Zamandan bağımsız bileşen analizi (tICA)46,47,48 projeksiyonu için giriş parametreleri olarak protein ve DNA arasındaki mesafe çiftlerini seçin. Bunu yapmak için GROMACS'taki make_ndx komutunu kullanın:
      gmx_mpi make_ndx -f girişi.pdb -o index.ndx
      NOT: Burada, DNA nükleotidinin O1P O2P ve N6 atomları ile eşleşen DNA nükleotidi (A14-20) ile eşleşen protein CA atomları ve kalıntı Y119, K122, K125, R131, Y133, Q117, Y134, K118, Q121 kalıntısının ağır atomları (NH1, NH2, OH, NZ, NE2, ND2) seçilmiştir. T19-23). Seçilen amino asitler kararlı HB'ler veya DNA ile tuz köprüleri oluşturabilir.
    3. Yukarıda seçilen atom dizinini index.ndx dosyasından yeni bir metin dosyasına (index.dat) kopyalayın. Bu atomlar arasındaki çift bilgisini python betiği ile Ek Dosya 1 generate_atom_indices.py ve şunu yazın:
      python2.6 generate_atom_indices.py indeksi.dat > AtomIndexces.txt
      Bu, protein ve DNA arasındaki 415 mesafe çiftini üretir.
    4. MSMbuilder komut penceresine aşağıdaki komutu yazarak her yörüngeden 415 uzaklık çiftini hesaplayın:
      msmb AtomPairsFeaturizer -out pair_features --pair_indices AtomIndexces.txt --top references.pdb --trjs "yörüngeler/*.xtc" --dönüştürülmüş pair_features --adım 5
    5. Aşağıdakileri yazarak verilerin boyutunu zamandan bağımsız ilk 2 bileşene (tIC) veya vektöre indirgemek için tICA uygulayın:
      msmb tICA -i .. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gama 0,05 -t tica_results,s5
      NOT: tICA, simülasyon sisteminin denklem tarafından en yavaş gevşeme serbestlik derecelerini belirlemek için zaman gecikmeli korelasyon matrisinin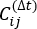 figure-protocol-6186 özdeğerini hesaplayan bir boyut indirgeme yöntemidir: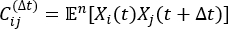
      figure-protocol-6310
      burada X i(t), t zamanındaki i-th reaksiyon koordinatının değeridir ve X j(t+Δ t), t+Δ t zamanındaki j-th reaksiyon koordinatının değeridir.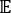 figure-protocol-6615 Xi(t) ve X j(t + Δ t) genel simülasyon yörüngelerinin ürününün beklenti değeridir. En yavaş gevşeyen serbestlik dereceleri boyunca yönler, yukarıdaki zaman gecikmeli korelasyon matrisinin 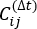figure-protocol-6937en büyük özdeğerlerine karşılık gelir. Burada, 2 tIC, MSM yapımızdaki üç makro durumu ayırt etmek için minimal bir set gibi görünmektedir (daha sonra ele alınacaktır). Örneğin, kullanılacak en uygun bileşen kümesini keşfetmek için genelleştirilmiş matris Rayleigh bölümü (GMRQ) puanı49'u da hesaplayabilirsiniz.
    6. Öngörülen veri kümelerini K-center43,44 yöntemiyle 100 kümede kümelemek için MSMbuilder'da komutu kullanın (bkz. Şekil 1B):
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 100.
      MD simülasyonlarının 2. turu için başlangıç yapısı olarak her kümenin merkez yapısını seçin. Hızlar hariç, konumlar, sıcaklıklar, basınçlar vb. dahil olmak üzere simüle edilmiş 100 yapının simülasyon bilgilerini koruyun.
      NOT: 25 simülasyonun ilk turundan sonra, ilk yolun belleği azaltıldı, bu nedenle konformasyonel örneklemeleri önemli ölçüde genişletmek için ikinci turda daha fazla küme, örneğin 100 küme üretiyoruz.
  4. 2. tur kapsamlı MD simülasyonlarının yürütülmesi
    1. Tüm atomlara rastgele başlangıç hızları uyguladıktan sonra bu 100 başlangıç yapısından başlayarak 60-ns MD simülasyonları yapın. mdp dosyasındaki hız üretimini açarak, yani md.mdp dosyasını gen_vel = hayır olarak değiştirerek rastgele başlangıç hızlarını ekleyin gen_vel = evet.
    2. Adım 1.3.1'de açıklandığı gibi her simülasyonun ilk 10 n'sini kaldırın, MSM'yi oluşturmak için 100 × 50 ns yörüngelerinden eşit olarak 2.500.000 anlık görüntü toplayın.
      NOT: Daha sonraki makrostat yapımında, özellikle düşük nüfuslu (X-Θ düzleminin dibinde ~% 0.2) az sayıda yol dışı durumun bulunduğunu unutmayın. Bu yol dışı durumlar, toplam makro durum sayısı 3 ile 6 arasında ayarlandığında bir makro durum olarak sınıflandırılır (Şekil 2B). Bu kadar düşük nüfuslu bir makrostat, sonunda kaldırılan sadece 3 yörünge içerdiğinden, bu protokolde gösterilen sonuçlar gerçekten de 97 × 50 ns yörüngeden, toplam 2.425.000 kare veya anlık görüntü ile elde edilmiştir.
  5. 2. tur MD yörüngelerinin kümelenmesi
    1. Daha önce yapıldığı gibi 2. tur yörüngeleri için tICA yapın. MSMbuilder yazın:
      msmb tICA -i .. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gama 0,05 -t tica_results,s5
    2. Korelasyon gecikme süresi Δt ve mikrostat sayıları için parametreleri doğrulamak için zımni zaman ölçeğini hesaplayın (bkz . Şekil 1C),
      figure-protocol-9653
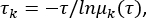
      burada τ, geçiş olasılığı matrisini (TPM) oluşturmak için kullanılan gecikme süresini temsil eder; μk(τ), TPM'nin kth özdeğerini τ gecikme süresi altında temsil eder. Bu python için Ek Dosya 1'deki python betiğini kullanın BuildMSMsAsVaryLagTime.py -d .. / -f .. /trajlist_num -i 50 -m 1000 -t 10 -n 20 -s 500.
    3. Yukarıda kullanılan parametreleri değiştirerek gecikme süresi τ ve mikrostat sayısını değiştirin:
      python BuildMSMsAsVaryLagTime.py -d .. / -f .. /trajlist_num -i 50 -m 1000 -t 5 10 20 30 40 -n 20 -s 20 200 400 500 800 2000 2000
      NOT: Sistem, ima edilen zaman ölçeği eğrileri zaman ölçeği ayrımı ile dengelenmeye başladığında Markovian olarak kabul edilir. Ardından, korelasyon gecikme süresi olarak Dt değerini ve MSM oluşturmak için ima edilen zaman ölçeğinin seviyelendirilmeye başladığı τ gecikme süresini seçin.
    4. Buna göre, nispeten büyük (ancak çok büyük olmayan) bir durum sayısı, N = 500 ve nispeten kısa bir korelasyon gecikme süresi Δt = 10 ns seçin. MSM oluşturmak için gecikme süresinin τ = 10 ns olduğu bulunmuştur.
    5. Komutu kullanarak konformasyonları 500 küme halinde sınıflandırın (bkz. Şekil 1B):
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 500
  6. MSM inşaatı
    1. Ek Dosya 1 python msm_lumping_usingPCCAplus.py'ndeki python betiğini kullanarak, MSMbuilder'daki PCCA + algoritması 50'ye göre en uygun makro durumların sayısını bulmak için500 mikrostatı 3-6 makro duruma toplayın. Biyomoleküllerin en önemli konformasyonel değişiklikleri için azaltılmış bir kinetik model ağı tanımlayın, az sayıda makrostat inşa ederek,yani aşağıda açıklandığı gibi yüzlerce mikrostatı kinetik olarak topaklayın.
    2. Yüksek boyutlu konformasyonları, adım 1.1.3 ve 1.1.4'te açıklandığı gibi her makrostat için X (DNA uzun ekseni boyunca protein hareketi) ve DNA boyunca proteinin dönme açısı ile eşleyin (örneğin, popülasyonu %1'< çok düşük olan hiçbir durum; bkz. Şekil 2C). Ardından sistemi en iyi temsil eden 3 makro durumu bulun (Şekil 1E). Proteinin DNA boyunca hareketinin ve DNA etrafındaki protein dönme açısının anlık görüntüleri için Şekil 2B'ye bakınız.
      NOT: 10 μs spontan protein ileri adım yolunu üreten önceki çalışmada, örneklemeleri orta derecede genişletmek için ek olarak 5 x 4 μs denge MD simülasyonları gerçekleştirdik. Orijinal ileri yolun haritalanmasını (bkz. Şekil 2A solda) ve daha önce yürütülen ileri yoldaki diğer 4-μs örnekleme yörüngelerini gösterdik (bkz. Şekil 2A sağ)8. Bu çalışmada kullanılan orijinal 100 × 50 ns (bkz. Şekil 2B sol)8 ve 97 × 50 ns yörüngelerinin haritalanması gösterilmiştir (bkz. Şekil 2B sağ).
  7. Ortalama ilk geçiş sürelerinin hesaplanması (MFPT)
    1. MC'nin zaman adımı olarak ayarlanan 10 ns gecikme süresi ile 500 mikro durum MSM'sinin TPM'sine dayalı beş adet 10 ms Monte Carlo (MC) yörüngesi yürütün. Ek Dosya 1 python mfpt_msm3.py'deki python betiği ile her makro durum çifti arasındaki MFPT52'yi hesaplayın (Şekil 3).
    2. Ek Dosya 2'deki bash dosyasını kullanarak MFPT'nin ortalama ve standart hatasını hesaplayın, şunu yazın:
      sh mfpt_analysis.bash

2. Uzun süreli dinamikleri örneklemek için kaba taneli (CG) simülasyon yapmak

  1. CafeMol 3.0 yazılımı30'u kullanarak bir CG simülasyonu gerçekleştirin. Giriş yapıları, simülasyon parametreleri, çıktı dosyaları vb. dahil olmak üzere .inp uzantılı giriş yapılandırma dosyasında belirtilen CG simülasyon ayarlarına bakın. CG benzetimini çalıştırmak için terminalde aşağıdaki komutu yazın:
    cafemol XXX.inp
  2. Giriş dosyasında, her blok etiketle < and ending with >başlayacak şekilde aşağıdaki blokları belirtin >>>.
    1. Çalışma dizinlerini ve giriş/çıkış dosya deposu yolunu belirtmek için dosya adları bloğunu (gerekli) ayarlayın. Bu benzetimlerin dosya adları bloğu için aşağıdakileri yazın:
      Dosya adlarını <<<<
      yol = XXXXX (çalışma yolu)
      filename = wrky (çıktı dosyası adları)
      ÇIKIŞ psf pdb film dcd rst
      path_pdb = XXXXX (giriş yerel yapı yolu)
      path_ini = XXXXX (giriş başlangıç yapısı yolu)
      path_natinfo = XXXXX (yerel bilgi dosyası yolu)
      path_para = XXXXX (parametre dosyaları yolu)
      >>>>
      NOT: Go-model53 , CG modellemesinde kullanıldığından, yani protein doğal konformasyona önyargılı olacağından, modellenen yapının doğal konformasyon olarak ayarlanması gerekir. Burada, giriş kristal yapısı doğal konformasyon olarak ayarlandı.
    2. Simülasyonların çalışma modunu tanımlamak için iş kontrol bloğunu (gerekli) ayarlayın. Aşağıdaki komutu yazın:
      <<<< job_cntl
      i_run_mode = 2 (= 2 sabit sıcaklık simülasyonu)
      i_simulate_type = 1 (=1 Langevin dinamiği)
      i_initial_state = 2 (=2, ilk yapılandırmanın Yerel yapılandırma olduğu anlamına gelir)
      >>>>
      Sabit sıcaklık Langevin dinamiği simülasyonlarını seçin.
    3. Giriş yapılarına ilişkin bilgileri tanımlamak için birimi ve durum bloğunu (gerekli) ayarlayın. Aşağıdaki komutu yazın:
      <<<< unit_and_state
      i_seq_read_style = 1 (=1, PDB dosyasından okuma dizileri anlamına gelir)
      i_go_native_read_style = 1 (=1, yerel yapının PDB dosyasından olduğu anlamına gelir)
      1 protein proteini.pdb (birim ve devlet molecular_type native_structure)
      2-3 dna DNA.pdb (birim ve devlet molecular_type native_structure)
      >>>>
      NOT: İlk giriş yapısı dosyaları (protein.pdb ve DNA.pdb burada) gereklidir. Yapılar pdb formatında yazılmıştır. Burada iki pdb dosyasına ihtiyaç vardır: biri WRKY'nin (ünite 1) ağır atom koordinatlarını içeren protein yapı dosyası, diğeri ise 200-bp çift sarmallı (ds) DNA'nın koordinatlarıdır (ünite 2-3). Protein başlangıçta DNA'dan 15 şuzağa yerleştirilir.
    4. energy_function bloğunda tanımlanan enerji fonksiyon bloğunu (gerekli) ayarlayın. Aşağıdaki komutu yazın:
      <<<< energy_function
      YEREL(1) L_GO
      YEREL(2-3) L_DNA2
      NLOCAL(1/1) GO EXV ELE
      NLOCAL(2-3/2-3) ELE DNA
      NLOCAL(1/2-3) EXV ELE
      i_use_atom_protein = 0
      i_use_atom_dna = 0
      i_para_from_ninfo = 1
      i_triple_angle_term = 2
      >>>>
      NOT: CG simülasyonlarında, protein, Go-model53 tarafından kaba tanelidir ve her amino asit, Cα konumuna yerleştirilmiş bir CG parçacığı ile temsil edilir. Protein konformasyonu, Go potansiyeli altında doğal yapıya veya buradaki kristal yapıya doğru önyargılı olacaktır (Şekil 4A solda). DNA, her nükleotidin sırasıyla şeker, fosfat ve azotlu baza karşılık gelen 3 CG parçacık S, P, N ile temsil edildiği 3SPN.2 model54 ile tanımlanır (Şekil 4A sağda). Elektrostatik ve vdW etkileşimleri farklı zincirler arasında değerlendirilir. CG simülasyonunda protein ve DNA arasındaki elektrostatik etkileşimler, Debye-Hückel potansiyeli55 ile yaklaştırılmıştır. VdW itici enerjisi, Go modelindeki ile aynı formu alır.
    5. Simülasyon bilgilerini tanımlamak için md_information bloğunu (gerekli) ayarlayın. Aşağıdaki komutu yazın:
      <<<< md_information
      n_step_sim = 1
      n_tstep(1) = 5000000000
      tstep_size = 0,1
      n_step_save = 1000
      n_step_neighbor = 100
      i_com_zeroing = 0
      i_no_trans_rot = 0
      tempk = 300,0
      n_seed = -1
      >>>>
      n_tstep simülasyon adımıdır. tstep_size her MD adımının zaman uzunluğu olarak ayarlayın, her CG Cafemol zaman adımı yaklaşık 200 fs 30'dur, bu nedenle buradaki her MD adımı prensipte200 × 0.1 fs'dir. Komşu listesini her 100 MD adımında bir güncelleyin (n_step_neighbor = 100). Simülasyon sıcaklığını 300 K'ya ayarlayın Berendsen termostatı56 ile protein yapısını güncellemek için hız tipi Verlet algoritmasını kullanarak sıcaklığı kontrol edin.
      NOT: n_step_sim, Go modeline dayalı potansiyelin havza numarası veya enerji eğrisinin yerel minimum sayısıdır. Çoklu havza potansiyeli, protein konformasyonunun farklı konformasyonlara önyargılı olmasına izin verir, böylece protein konformasyonu bir yerel minimumdan diğerine değişebilir. Burada sadece tek havza Go modeli kullanılır, bu da simülasyonlarda protein için sadece bir önyargılı konformasyon (kristal yapı) anlamına gelir. Bu arada, CG bağlamında modellenmiş protein-DNA hidrojen bağ etkileşimi vb. olmadığından, moleküler hareketler atomik simülasyonlardan 10 kat daha hızlı, yani > örneklenebilir.
    6. Elektrostatik etkileşim farklı zincirler arasında dikkate alındığından elektrostatik bloğu ayarlayın (yalnızca elektrostatik etkileşim kullanıldığında gereklidir), bu nedenle bu bloğu yazarak elektrostatik etkileşim parametrelerini tanımlamak için kullanın:
      <<<< elektrostatik
      cutoff_ele = 10.0
      ionic_strength = 0.15
      >>>>
      Elektrostatik etkileşimdeki Debye uzunluğunu, çözelti koşuluna karşılık gelen 10 şdeğerine ayarlayın. İyonik mukavemeti fizyolojik durumda olduğu gibi 0.15 M'ye ayarlayın.

Sonuçlar

Rotasyona bağlı kayar veya MSM konstrüksiyonundan WRKY'nin 1 bp kademelendirilmesi
DNA üzerindeki tüm protein konformasyonları, DNA boyunca protein COM'unun uzunlamasına hareketi X ve dönme açısı ile eşleştirilir (bkz. Şekil 3A). Bu iki derecenin doğrusal eşleşmesi, DNA üzerindeki WRKY alan proteininin rotasyonla eşleşmiş adımını gösterir. Konformasyonlar MSM'de 3 makro duruma (S1, S2 ve S3) daha fazla kümelenebilir. WRKY'nin ileri adımlanması ...

Tartışmalar

Bu çalışma, DNA boyunca hareket eden bir transkripsiyon faktörünü veya TF proteinini ortaya çıkarmak için yapı tabanlı hesaplamalı simülasyonun ve örneklemelerin nasıl yürütüleceğini, sadece adımlamanın atomik detayında değil, aynı zamanda DNA hedef aramasında TF'nin kolaylaştırılmış difüzyonu için gerekli olan işlemsel difüzyonda da ele almaktadır. Bunu yapmak için, homojen poli-A DNA boyunca 1-bp için küçük bir TF alan proteini WRKY adımının Markov durum modeli veya MSM'si ilk...

Açıklamalar

Yazarların çıkar çatışması yoktur.

Teşekkürler

Bu çalışma NSFC Grant #11775016 ve #11635002 tarafından desteklenmiştir. JY, NSF DMS 1763272) aracılığıyla UCI'nin CMCF'si ve UCI'dan Simons Vakfı hibe #594598 ve başlangıç fonu tarafından desteklenmiştir. LTD, Şangay Doğa Bilimleri Vakfı #20ZR1425400 ve #21JC1403100 tarafından desteklenmektedir. Pekin Hesaplamalı Bilim Araştırma Merkezi'nin (CSRC) hesaplama desteğini de kabul ediyoruz.

Malzemeler

NameCompanyCatalog NumberComments
CafeMolKyoto Universitycoarse-grained (CG) simulations
GROMACSUniversity of Groningen Royal Institute of Technology Uppsala Universitymolecular dynamics simulations software
MatlabMathWorksNumerical calculation software
MSMbuilderStanford Universitybuild MSM
VMDUNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGNmolecular visualization program

Referanslar

  1. Latchman, D. S. Transcription factors: an overview. The International Journal of Biochemistry & Cell Biology. 29 (12), 1305-1312 (1997).
  2. Berg, O. G., von Hippel, P. H. Selection of DNA binding sites by regulatory proteins. Statistical-mechanical theory and application to operators and promoters. Journal of Molecular Biology. 193 (4), 723-750 (1987).
  3. von Hippel, P. H., Berg, O. G. Facilitated target location in biological systems. The Journal of Biological Chemistry. 264 (2), 675-678 (1989).
  4. Halford, S. E., Marko, J. F. How do site-specific DNA-binding proteins find their targets. Nucleic Acids Research. 32 (10), 3040-3052 (2004).
  5. Slusky, M., Mirny, L. A. Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential. Biophysical Journal. 87 (6), 4021-4035 (2004).
  6. Bauer, M., Metzler, R. Generalized facilitated diffusion model for DNA-binding proteins with search and recognition states. Biophysical Journal. 102 (10), 2321-2330 (2012).
  7. Shvets, A. A., Kochugaeva, M. P., Kolomeisky, A. B. Mechanisms of Protein Search for Targets on DNA: Theoretical Insights. Molecules. 23 (9), 2106 (2018).
  8. Dai, L., Xu, Y., Du, Z., Su, X. D., Yu, J. Revealing atomic-scale molecular diffusion of a plant-transcription factor WRKY domain protein along DNA. Proceedings of the National Academy of Sciences of the United States of America. 118 (23), 2102621118 (2021).
  9. Chodera, J. D., Singhal, N., Pande, V. S., Dill, K. A., Swope, W. C. Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. The Journal of Chemical Physics. 126 (15), 155101 (2007).
  10. Pan, A. C., Roux, B. Building Markov state models along pathways to determine free energies and rates of transitions. The Journal of Chemical Physics. 129 (6), 064107 (2008).
  11. Bowman, G. R., Huang, X., Pande, V. S. Using generalized ensemble simulations and Markov state models to identify conformational states. Methods. 49 (2), 197-201 (2009).
  12. Prinz, J. H., et al. Markov models of molecular kinetics: Generation and validation. The Journal of chemical physics. 134 (17), 174105 (2011).
  13. Chodera, J. D., Noé, F. Markov state models of biomolecular conformational dynamics. Current Opinion in Structural Biology. 25, 135-144 (2014).
  14. Malmstrom, R. D., Lee, C. T., Van Wart, A. T., Amaro, R. E. On the Application of Molecular-Dynamics Based Markov State Models to Functional Proteins. Journal of Chemical Theory and Computation. 10 (7), 2648-2657 (2014).
  15. Husic, B. E., Pande, V. S. Markov State Models: From an Art to a Science. Journal of the American Chemical Society. 140 (7), 2386-2396 (2018).
  16. Sittel, F., Stock, G. Perspective: Identification of collective variables and metastable states of protein dynamics. The Journal of chemical physics. 149 (15), 150901 (2018).
  17. Wang, W., Cao, S., Zhu, L., Huang, X. Constructing Markov State Models to elucidate the functional conformational changes of complex biomolecules. WIREs Computational Molecular Science. 8, 1343 (2018).
  18. Peng, S., et al. Target search and recognition mechanisms of glycosylase AlkD revealed by scanning FRET-FCS and Markov state models. Proceedings of the National Academy of Sciences of the United States of America. 117 (36), 21889-21895 (2020).
  19. Tian, J., Wang, L., Da, L. T. Atomic resolution of short-range sliding dynamics of thymine DNA glycosylase along DNA minor-groove for lesion recognition. Nucleic Acids Research. 49 (3), 1278-1293 (2021).
  20. Chu, J. -. W., Izveko, S., Voth, G. The multiscale challenge for biomolecular systems: coarse-grained modeling. Molecular Simulation. 32 (3-4), 211-218 (2006).
  21. Marrink, S. J., Risselada, H. J., Yefimov, S., Tieleman, D. P., De Vries, A. H. The MARTINI force field: coarse grained model for biomolecular simulations. The Journal of Physical Chemistry B. 111 (27), 7812-7824 (2007).
  22. Givaty, O., Levy, Y. Protein sliding along DNA: dynamics and structural characterization. Journal of Molecular Biology. 385 (4), 1087-1097 (2009).
  23. Khazanov, N., Levy, Y. Sliding of p53 along DNA can be modulated by its oligomeric state and by cross-talks between its constituent domains. Journal of Molecular Biology. 408 (2), 335-355 (2011).
  24. Riniker, S., Allison, J. R., van Gunsteren, W. F. On developing coarse-grained models for biomolecular simulation: a review. Physical Chemistry Chemical Physics : PCCP. 14 (36), 12423-12430 (2012).
  25. Kmiecik, S., et al. Coarse-Grained Protein Models and Their Applications. Chemical Reviews. 116 (14), 7898-7936 (2006).
  26. Bhattacherjee, A., Krepel, D., Levy, Y. Coarse-grained models for studying protein diffusion along DNA. WIREs Computational Molecular Science. 6, 515-531 (2016).
  27. Wang, J., et al. Machine Learning of Coarse-Grained Molecular Dynamics Force Fields. ACS Central Science. 5 (5), 755-767 (2019).
  28. Joshi, S. Y., Deshmukh, S. A. A review of advancements in coarse-grained molecular dynamics simulations. Molecular Simulation. 47 (10-11), 786-803 (2021).
  29. Bigman, L. S., Greenblatt, H. M., Levy, Y. What Are the Molecular Requirements for Protein Sliding along DNA. The Journal of Physical Chemistry B. 125 (12), 3119-3131 (2021).
  30. Kenzaki, H., et al. CafeMol: A Coarse-Grained Biomolecular Simulator for Simulating Proteins at Work. Journal of Chemical Theory and Computation. 7 (6), 1979-1989 (2011).
  31. Berendsen, H. J. C., vander Spoel, D., van Drunen, R. GROMACS: a message-passing parallel molecular dynamics implementation. Computer Physics Communications. 91 (1-3), 43-56 (1995).
  32. vander Spoel, D., et al. GROMACS: fast, flexible, and free. Journal of Computational Chemistry. 26 (16), 1701-1718 (2005).
  33. Abraham, M. J., et al. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 1-2, 19-25 (2015).
  34. Harrigan, M. P., et al. MSMBuilder: Statistical Models for Biomolecular Dynamics. Biophysical journal. 112 (1), 10-15 (2017).
  35. Humphrey, W., Dalke, A., Schulten, K. VMD: visual molecular dynamics. Journal of Molecular Graphics. 14 (1), 33-38 (1996).
  36. Izrailev, S., et al. Steered Molecular Dynamics. Computational Molecular Dynamics: Challenges, Methods, Ideas. 4, 39-65 (1999).
  37. Schlitter, J., Engels, M., Krüger, P. Targeted molecular dynamics: a new approach for searching pathways of conformational transitions. Journal of Molecular Graphics. 12 (2), 84-89 (1994).
  38. Maragliano, L., Fischer, A., Vanden-Eijnden, E., Ciccotti, G. String method in collective variables: minimum free energy paths and isocommittor surfaces. The Journal of Chemical Physics. 125 (2), 24106 (2006).
  39. Weiss, D. R., Levitt, M. Can morphing methods predict intermediate structures. Journal of Molecular Biology. 385 (2), 665-674 (2009).
  40. Xu, Y. P., Xu, H., Wang, B., Su, X. D. Crystal structures of N-terminal WRKY transcription factors and DNA complexes. Protein. 11 (3), 208-213 (2020).
  41. Higham, D. J., Higham, N. J. MATLAB guide. Society for Industrial and Applied Mathematics. , (2016).
  42. Hartigan, J. A., Wong, M. A. Algorithm AS 136: A K-Means Clustering Algorithm. Journal of the Royal Statistical Society. Series C (Applied Statistics). 28 (1), 100-108 (1979).
  43. Gonzalez, T. F. Clustering to minimize the maximum intercluster distance. Theoretical Computer Science. 38, 293-306 (1985).
  44. Zhao, Y., Sheong, F. K., Sun, J., Sander, P., Huang, X. A fast parallel clustering algorithm for molecular simulation trajectories. Journal of Computational Chemistry. 34 (2), 95-104 (2013).
  45. Ivani, I., et al. Parmbsc1: a refined force field for DNA simulations. Nature Methods. 13 (1), 55-58 (2016).
  46. Naritomi, Y., Fuchigami, S. Slow dynamics of a protein backbone in molecular dynamics simulation revealed by time-structure based independent component analysis. The Journal of Chemical Physics. 139 (21), 215102 (2013).
  47. Naritomi, Y., Fuchigami, S. Slow dynamics in protein fluctuations revealed by time-structure based independent component analysis: the case of domain motions. The Journal of Chemical Physics. 134 (6), 065101 (2011).
  48. Pérez-Hernández, G., Paul, F., Giorgino, T., De Fabritiis, G., Noé, F. Identification of slow molecular order parameters for Markov model construction. The Journal of Chemical Physics. 139 (1), 015102 (2013).
  49. McGibbon, R. T., Pande, V. S. Variational cross-validation of slow dynamical modes in molecular kinetics. The Journal of Chemical Physics. 142 (12), 124105 (2015).
  50. Deuflhard, P., Weber, M. Robust Perron cluster analysis in conformation dynamics. Linear Algebra and its Applications. 398, 161-184 (2005).
  51. Silva, D. A., et al. Millisecond dynamics of RNA polymerase II translocation at atomic resolution. Proceedings of the National Academy of Sciences of the United States of America. 111 (21), 7665-7670 (2014).
  52. Swope, W. C., Pitera, J. W., Suits, F. Describing Protein Folding Kinetics by Molecular Dynamics Simulations. 1. Theory. The Journal of Physical Chemistry B. 108 (21), 6571-6581 (2004).
  53. Clementi, C., Nymeyer, H., Onuchic, J. N. Topological and energetic factors: what determines the structural details of the transition state ensemble and "en-route" intermediates for protein folding? An investigation for small globular proteins. Journal of molecular biology. 298 (5), 937-953 (2000).
  54. Hinckley, D. M., Freeman, G. S., Whitmer, J. K., De Pablo, J. J. An experimentally-informed coarse-grained 3-Site-Per-Nucleotide model of DNA: structure, thermodynamics, and dynamics of hybridization. The Journal of chemical physics. 139 (14), 144903 (2013).
  55. Debye, P., Huckel, E. The theory of the electrolyte II-The border law for electrical conductivity. Physikalische Zeitschrift. 24, 305-325 (1923).
  56. Berendsen, H. J., Postma, J. V., van Gunsteren, W. F., DiNola, A., Haak, J. R. Molecular dynamics with coupling to an external bath. The Journal of Chemical Physics. 81, 3684-3690 (1984).
  57. Bowman, G. R. Improved coarse-graining of Markov state models via explicit consideration of statistical uncertainty. The Journal of Chemical Physics. 137 (13), 134111 (2012).
  58. Jain, A., Stock, G. Identifying metastable states of folding proteins. Journal of Chemical Theory and Computation. 8 (10), 3810-3819 (2012).
  59. Röblitz, S., Weber, M. Fuzzy spectral clustering by PCCA+: application to Markov state models and data classification. Advances in Data Analysis and Classification. 7, 147-179 (2013).
  60. Mardt, A., Pasquali, L., Wu, H., Noé, F. VAMPnets for deep learning of molecular kinetics. Nature Communications. 9 (1), 5 (2018).
  61. Wang, W., Liang, T., Sheong, F. K., Fan, X., Huang, X. An efficient Bayesian kinetic lumping algorithm to identify metastable conformational states via Gibbs sampling. The Journal of Chemical Physics. 149 (7), 072337 (2018).
  62. Chen, W., Sidky, H., Ferguson, A. L. Nonlinear discovery of slow molecular modes using state-free reversible VAMPnets. The Journal of Chemical Physics. 150 (21), 214114 (2019).
  63. Gu, H., et al. RPnet: a reverse-projection-based neural network for coarse-graining metastable conformational states for protein dynamics. Physical Chemistry Chemical Physics :PCCP. 24 (3), 1462-1474 (2022).
  64. Lane, T. J., Bowman, G. R., Beauchamp, K., Voelz, V. A., Pande, V. S. Markov state model reveals folding and functional dynamics in ultra-long MD trajectories. Journal of the American Chemical Society. 133 (45), 18413-18419 (2011).
  65. Konovalov, K. A., Unarta, I. C., Cao, S., Goonetilleke, E. C., Huang, X. Markov State Models to Study the Functional Dynamics of Proteins in the Wake of Machine Learning. JACS Au. 1 (9), 1330-1341 (2021).
  66. Cao, S., Montoya-Castillo, A., Wang, W., Markland, T. E., Huang, X. On the advantages of exploiting memory in Markov state models for biomolecular dynamics. The Journal of Chemical Physics. 153 (1), 014105 (2020).
  67. Brandani, G. B., Takada, S. Chromatin remodelers couple inchworm motion with twist-defect formation to slide nucleosomal DNA. PLoS Computational Biology. 14 (11), 1006512 (2018).
  68. Tan, C., Terakawa, T., Takada, S. Dynamic Coupling among Protein Binding, Sliding, and DNA Bending Revealed by Molecular Dynamics. Journal of the American Chemical Society. 138 (27), 8512-8522 (2016).
  69. Terakawa, T., Takada, S. p53 dynamics upon response element recognition explored by molecular simulations. Scientific reports. 5, 17107 (2015).
  70. Brandani, G. B., Niina, T., Tan, C., Takada, S. DNA sliding in nucleosomes via twist defect propagation revealed by molecular simulations. Nucleic Acids Research. 46 (6), 2788-2801 (2018).
  71. Knotts, T. A., Rathore, N., Schwartz, D. C., de Pablo, J. J. A coarse grain model for DNA. The Journal of Chemical Physics. 126 (8), 084901 (2007).
  72. Freeman, G. S., Hinckley, D. M., Lequieu, J. P., Whitmer, J. K., de Pablo, J. J. Coarse-grained modeling of DNA curvature. The Journal of Chemical Physics. 141 (16), 165103 (2014).

Yeniden Basımlar ve İzinler

Bu JoVE makalesinin metnini veya resimlerini yeniden kullanma izni talebi

Izin talebi

Daha Fazla Makale Keşfet

BiyolojiSay 181

This article has been published

Video Coming Soon

JoVE Logo

Gizlilik

Kullanım Şartları

İlkeler

Bize Ulaşın

KÜTÜPHANEYE TAVSİYE ET

JoVE HABER BÜLTENLERİ

Araştırma

Eğitim

Yazarlar

Kütüphaneciler

JoVE Hakkında

Telif Hakkı © 2020 MyJove Corporation. Tüm hakları saklıdır