Simulación basada en la estructura y muestreo de los movimientos de proteínas del factor de transcripción a lo largo del ADN desde el paso a escala atómica hasta la difusión de grano grueso

Resumen

El objetivo de este protocolo es revelar la dinámica estructural de la difusión unidimensional de la proteína a lo largo del ADN, utilizando una proteína de dominio WRKY del factor de transcripción vegetal como un sistema ejemplar. Para ello, se han implementado simulaciones de dinámica molecular tanto atomísticas como de grano grueso junto con extensos muestreos computacionales.

Resumen

El deslizamiento unidimensional (1-D) de la proteína del factor de transcripción (TF) a lo largo del ADN es esencial para facilitar la difusión del TF para localizar el sitio de ADN objetivo para la regulación genética. La detección de la resolución de par de bases (bp) del TF deslizando o pisando el ADN sigue siendo un desafío experimental. Recientemente hemos realizado simulaciones de dinámica molecular (DM) de todos los átomos que capturan el paso espontáneo de 1 pb de una pequeña proteína TF del dominio WRKY a lo largo del ADN. Basado en la ruta de paso WRKY de 10 μs obtenida de tales simulaciones, el protocolo aquí muestra cómo realizar muestreos conformacionales más extensos de los sistemas TF-DNA, mediante la construcción del modelo de estado de Markov (MSM) para el paso de proteína de 1 pb, con varios números de micro y macro estados probados para la construcción de MSM. Con el fin de examinar la búsqueda de difusión 1-D procesiva de la proteína TF junto con el ADN con base estructural, el protocolo muestra además cómo realizar simulaciones de MD de grano grueso (CG) para muestrear la dinámica a escala a largo plazo del sistema. Tales modelos y simulaciones de CG son particularmente útiles para revelar los impactos electrostáticos proteína-ADN en los movimientos de difusión procesivos de la proteína TF por encima de decenas de microsegundos, en comparación con los movimientos de paso de proteínas de submicrosegundos a microsegundos revelados a partir de las simulaciones de todos los átomos.

Introducción

Los factores de transcripción (TF) buscan que el ADN objetivo se una y regule la transcripción de genes y las actividades relacionadas¹. Aparte de la difusión tridimensional (3D), se ha sugerido que la difusión facilitada de TF es esencial para la búsqueda de ADN objetivo, en la que las proteínas también pueden deslizarse o saltar a lo largo del ADN unidimensional (1D), o saltar con transferencia intersegmental en el ADN 2,3,4,5,6,7.

En un estudio reciente, hemos realizado decenas de simulaciones de dinámica molecular (MD) de equilibrio de todos los átomos (μs) en una planta TF, la proteína del dominio WRKY en el ADN⁸. Se ha capturado un paso completo de 1 pb de WRKY en ADN poli-A en microsegundos. Se han observado los movimientos de la proteína a lo largo del surco del ADN y la dinámica de ruptura-reforma de los enlaces de hidrógeno (HB). Si bien tal trayectoria representa un camino muestreado, todavía falta un panorama general de pasos de proteínas. Aquí, mostramos cómo expandir los muestreos computacionales alrededor de la ruta de paso de la proteína capturada inicialmente con el modelo de estado de Markov (MSM) construido, que se han implementado ampliamente para simular una variedad de sistemas biomoleculares que involucran cambios conformacionales sustanciales y separación a escala de tiempo 9,10,11,12,13,14,15,16, 17,18,19. El propósito es revelar el conjunto conformacional y los estados metaestables de la difusión de la proteína TF a lo largo del ADN durante un paso cíclico.

Si bien la simulación MD anterior revela la resolución atómica de los movimientos de proteínas para 1 pb en el ADN, la dinámica estructural de la difusión procesiva a largo plazo del TF a lo largo del ADN a la misma alta resolución es difícilmente accesible. Sin embargo, la realización de simulaciones de MD de grano grueso (CG) a nivel de residuo es técnicamente accesible. La escala de tiempo de simulación CG se puede extender efectivamente a decenas o cientos de veces más que las simulaciones atómicas 20,21,22,23,24,25,26,27,28,29. Aquí, mostramos las simulaciones CG realizadas mediante la implementación del software CafeMol desarrollado por Takada lab³⁰.

En el protocolo actual, presentamos primero las simulaciones atómicas de la proteína del dominio WRKY a lo largo del ADN poli-A y la construcción de MSM, que se centran en el muestreo de los movimientos de paso de la proteína para solo 1 pb a lo largo del ADN. A continuación presentamos el modelado CG y las simulaciones del mismo sistema proteína-ADN, que extienden el muestreo computacional a la difusión procesiva de proteínas sobre decenas de bps a lo largo del ADN.

Aquí, utilizamos el software GROMACS^31,32,33 para realizar simulaciones de MD y MSMbuilder³⁴ para construir el MSM para instantáneas conformacionales muestreadas, así como para usar VMD³⁵ para visualizar las biomoléculas. El protocolo requiere que el usuario pueda instalar e implementar el software anterior. La instalación e implementación del software CafeMol³⁰ es necesaria para realizar las simulaciones CG MD. También se realizan análisis adicionales de las trayectorias y la visualización en VMD.

Protocolo

1. Construcción del modelo de estado de Markov (MSM) a partir de simulaciones de MD atómica

1. Vía de paso espontánea de proteínas y recolección de estructuras iniciales
   1. Utilice una trayectoria MD de 10 μs de todo átomo⁸ obtenida previamente para extraer 10000 fotogramas de manera uniforme de un camino de paso "hacia adelante" de 1 pb (es decir, un fotograma por cada nanosegundo). El número total de marcos debe ser lo suficientemente grande como para incluir todas las conformaciones representativas.
   2. Prepare la ruta de transición con 10000 fotogramas en VMD haciendo clic en Archivo > Guardar coordenadas, escriba proteína o nucleico en el cuadro átomos seleccionados y elija fotogramas en el cuadro Marcos, haga clic en Guardar para obtener los fotogramas necesarios.
      NOTA: Se utilizó una trayectoria de simulación MD de 10 μs de todos los átomos obtenida previamente (llamada "trayectoria de paso hacia adelante" aquí) para la distancia de paso WRKY de 1 pb en un ADN poli-A^{homogéneo de} 34 pb 8 como la ruta inicial para lanzar más muestreos conformacionales. Tenga en cuenta que en la mayoría de las prácticas, sin embargo, se construye una ruta inicial, mediante la realización de simulaciones de MD dirigidas o dirigidas, o la implementación de métodos generales de generación de rutas, ^{etc.36,37,38,39}.
   3. Alinee el eje largo del ADN de referencia (de la estructura cristalina) con el eje x y establezca el centro de masa inicial (COM) del ADN completo de 34 pb en el origen del espacio de coordenadas para la conveniencia de un análisis de datos adicional. Para ello, haga clic en Extensiones > consola de Tk en VMD y escriba en la ventana de comandos de la consola de Tk:
      fuente rotate.tcl
      El script tcl se puede encontrar en el archivo complementario 3.
   4. Luego calcule la distancia cuadrática media de la raíz (RMSD) de la columna vertebral de la proteína alineando el ADN central de 10 pb (A 14 a 23 y T 14' a 23') con el de la estructura cristalina⁴⁰, y el RMSD representa medidas geométricas de los sistemas (ver Figura 1A). Para ello, haga clic en VMD > Extensiones > análisis > herramienta de trayectoria RMSD y escriba nucleico y residuo 14 a 23 y 46 a 55 en el cuadro de selección de átomos, haga clic en Alinear y, a continuación, en el cuadro RMSD para calcular los valores RMSD.
   5. Calcular el grado de rotación de la proteína alrededor del ADN Θ(t) en el plano y-z en MATLAB escribiendo el comando
      rad2deg(atan(z/y))
      con el posicionamiento angular inicial definido como Θ(0)=0, como se realizó anteriormente⁸.
   6. Escriba el siguiente comando en MATLAB⁴¹ para utilizar los métodos K-means 42,43,44 y clasifique las 10000 estructuras en 25 clústeres escribiendo:
      [idx, C]=kmeans( X, 25)
      aquí X es una matriz 2D de RMSD y ángulo de rotación de WRKY en el ADN. Reúna las estructuras de estos 25 centros de clúster para simulaciones de MD adicionales.
      NOTA: Dado que la proteína RMSD muestreada en relación con el ADN cubre un rango de aproximadamente 25 Å, elegimos 25 grupos para tener un grupo por angstrom.
2. Realización de la^1ª ronda de simulaciones md y los ajustes de simulación
   1. Construya sistemas atomísticos para las 25 estructuras utilizando el software GROMACS 5.1.2³² bajo el campo de fuerza parmbsc1⁴⁵ y utilizando el archivo buildsystem.sh del archivo complementario 2 en shell.
   2. Realice simulaciones de MD de 60-ns para estos 25 sistemas bajo conjunto NPT con un paso de tiempo de 2 fs escribiendo el siguiente comando en shell:
      gmx_mpi grompp -f md.mdp -c npt.gro -p topol.top -o md.tpr
      gmx_mpi mdrun -deffnm md
3. Agrupación de los 1^c trayectorias redondas de MD
   1. Elimine los primeros 10 ns de cada trayectoria de simulación escribiendo en shell:
      gmx_mpi trjcat -f md.xtc -b 10000 -e 600000 -o newtraj.xtc
      y recolectar conformaciones de las trayectorias de 25 × 50 ns para clustering a fin de preparar las estructuras de entrada para los muestreos posteriores más extensos (simulaciones MD^{de 2ª} ronda).
      NOTA: Para reducir el impacto de la trayectoria inicial y permitir el equilibrio local, se eliminaron 10-ns del período inicial de simulaciones.
   2. Elija pares de distancia entre proteína y ADN como parámetros de entrada para la proyección de análisis de componentes independientes del tiempo (tICA)^46,47,48. Utilice el comando make_ndx en GROMACS para hacer esto:
      gmx_mpi make_ndx -f input.pdb -o index.ndx
      NOTA: Aquí, se seleccionaron los átomos de proteína CA y los átomos pesados (NH1, NH2, OH, NZ, NE2, ND2) del residuo Y119, K122, K125, R131, Y133, Q146, K144, R135, W116, R117, Y134, K118, Q121 que pueden formar enlaces de hidrógeno (HB) con el nucleótido de ADN, que se emparejan con los átomos O1P O2P y N6 del nucleótido de ADN (A14-20, T19-23). Los aminoácidos seleccionados pueden formar HB estables o puentes de sal con ADN.
   3. Copie el índice de átomo seleccionado anteriormente del archivo index.ndx a un nuevo archivo de texto (index.dat). Obtenga la información del par entre estos átomos mediante el script python del archivo complementario 1 generate_atom_indices.py y escriba:
      índice de generate_atom_indices.py python2.6.dat > AtomIndices.txt
      Esto genera los 415 pares de distancia entre la proteína y el ADN.
   4. Calcule los 415 pares de distancia de cada trayectoria escribiendo el siguiente comando en la ventana de comandos de MSMbuilder:
      msmb AtomPairsFeaturizer -out pair_features --pair_indices AtomIndices.txt --top references.pdb --trjs "trajectories/*.xtc" --transformed pair_features --stride 5
   5. Realice tICA para reducir la dimensión de los datos en los primeros 2 componentes independientes del tiempo (tIC) o vectores escribiendo:
      msmb tICA -i.. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gamma 0.05 -t tica_results.h5
      NOTA: tICA es un método de reducción de dimensiones que calcula el valor propio de la matriz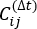 de correlación con retraso en el tiempo para determinar los grados de libertad relajantes más lentos del sistema de simulación mediante la ecuación: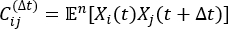
      
      donde X_i(t) es el valor de la coordenada de reacción i-ésima en el tiempo t, y X_j(t+Δt) es el valor de la coordenada de reacción j-ésima en el tiempo t+Δt.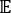 es el valor esperado del producto de las trayectorias de simulación general X_i(t) y X_j(t + Δt). Las direcciones a lo largo de los grados de libertad relajantes más lentos corresponden a los valores propios más grandes de la matriz 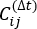de correlación con retraso en el tiempo anterior. Aquí, 2 tIC parecen ser un conjunto mínimo para diferenciar tres macroestados en nuestra construcción de MSM (abordada más adelante). También se puede calcular la puntuación⁴⁹ del cociente de Rayleigh de la matriz generalizada (GMRQ), por ejemplo, para explorar un conjunto óptimo de componentes que se utilizarán.
   6. Utilice el comando en MSMbuilder para agrupar los conjuntos de datos proyectados en 100 clústeres mediante el método K-center^43,44 (consulte la Figura 1B):
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 100.
      Seleccione la estructura central de cada clúster como estructura inicial para la^2ª ronda de simulaciones md. Mantener la información de simulación de las 100 estructuras simuladas, incluyendo posiciones, temperaturas, presiones, etc., excepto las velocidades.
      NOTA: Después de la primera ronda de 25 simulaciones, la memoria de la ruta inicial se ha reducido, por lo que generamos más clústeres, por ejemplo, 100 clústeres, en la segunda ronda, para ampliar sustancialmente los muestreos conformacionales.
4. Realización de la^2ª ronda de extensas simulaciones de MD
   1. Realizar simulaciones de 60-ns MD a partir de estas 100 estructuras iniciales después de imponer velocidades iniciales aleatorias en todos los átomos. Agregue las velocidades iniciales aleatorias activando la generación de velocidad en el archivo mdp, es decir, cambiando el archivo md.mdp gen_vel = no a gen_vel = sí.
   2. Elimine los primeros 10 ns de cada simulación como se describe en el paso 1.3.1, recopile 2.500.000 instantáneas de las trayectorias de 100 × 50 ns de manera uniforme para construir el MSM.
      NOTA: Tenga en cuenta que en la construcción posterior de macroestados, se encontró un pequeño número de estados fuera de ruta con una población particularmente baja (~ 0.2%, en la parte inferior del plano X-Θ). Estos estados fuera de ruta se clasifican como un macroestado cuando el número total de macroestados se establece como 3 a 6 (Figura 2B). Dado que un macroestado poblacional tan bajo incluye solo 3 trayectorias, que se eliminaron al final, los resultados mostrados en este protocolo se obtuvieron de hecho de 97 × 50 trayectorias ns, con un total de 2.425.000 fotogramas o instantáneas.
5. Agrupación de las trayectorias de MD^{de la 2ª} ronda
   1. Realizar tICA para las trayectorias^{de la 2ª} ronda como se hizo anteriormente. Escriba en MSMbuilder:
      msmb tICA -i.. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gamma 0.05 -t tica_results.h5
   2. Calcular la escala de tiempo implícita para validar los parámetros para el tiempo de retardo de correlación Δt y los números de microestados (ver Figura 1C),
      
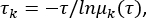
      donde τ representa el tiempo de retraso utilizado para construir la matriz de probabilidad de transición (TPM); μ_k(τ) representa el késimo valor propio del TPM bajo un tiempo de retraso de τ. Utilice el script python del archivo suplementario 1 para este python BuildMSMsAsVaryLagTime.py -d .. / -f.. /trajlist_num -i 50 -m 1000 -t 10 -n 20 -s 500.
   3. Varíe el número de tiempo de retraso τ y microestados cambiando los parámetros utilizados anteriormente:
      python BuildMSMsAsVaryLagTime.py -d.. / -f.. /trajlist_num -i 50 -m 1000 -t 5 10 20 30 40 -n 20 -s 20 200 400 500 800 2000
      NOTA: El sistema se considera Markovian cuando las curvas de escala de tiempo implícitas comienzan a nivelarse con la separación de escala de tiempo. Luego, elija el Dt como el tiempo de retraso de correlación, y el τ el tiempo de retraso donde la escala de tiempo implícita comienza a nivelarse para construir MSM.
   4. En consecuencia, elija un número comparativamente grande (pero no demasiado grande) de estados, N = 500, y un tiempo de retardo de correlación comparativamente corto Δt = 10 ns. Se encontró que el tiempo de retraso era τ = 10 ns para construir MSM.
   5. Clasifique las conformaciones en 500 clústeres (consulte la Figura 1D) mediante el comando:
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 500
6. Construcción de HSH
   1. Agrupe los 500 microestados en 3–6 macroestados para averiguar el número de macroestados que mejor se adapten según el algoritmo PCCA +⁵⁰ en MSMbuilder, utilizando el script python en el archivo suplementario 1 python msm_lumping_usingPCCAplus.py. Identificar una red cinética reducida de modelos para los cambios conformacionales más esenciales de las biomoléculas, mediante la construcción de un pequeño número de macroestados, es decir, sobre la agrupación cinética de cientos de microestados como se describe a continuación^17,51.
   2. Mapee las conformaciones de alta dimensión al X (movimiento de la proteína a lo largo del eje largo del ADN) y al ángulo de rotación de la proteína a lo largo del ADN para cada macroestado como se describe en los pasos 1.1.3 y 1.1.4 (por ejemplo, ningún estado con una población demasiado baja < 1%; ver Figura 2C). A continuación, busque los 3 macroestados que mejor representan el sistema (Figura 1E). Consulte la Figura 2D para obtener instantáneas del movimiento de la proteína a lo largo del ADN y el ángulo de rotación de la proteína alrededor del ADN.
      NOTA: En trabajos anteriores que generaron la ruta de paso hacia adelante de la proteína espontánea de 10 μs, también realizamos simulaciones de MD de equilibrio de 5 x 4 μs para expandir moderadamente los muestreos. Mostramos el mapeo de la trayectoria hacia adelante original (ver Figura 2A izquierda) y otras trayectorias de muestreo de 4 μs en la trayectoria hacia adelante realizadas previamente (ver Figura 2A derecha)⁸. Se muestra el mapeo de los 100 × 50 ns originales (ver Figura 2B izquierda)⁸ y las trayectorias de 97 × 50 ns utilizadas en este trabajo (ver Figura 2B derecha).
7. Cálculo de los tiempos medios de primer paso (MFPT)
   1. Realice cinco trayectorias monte carlo (MC) de 10 ms basadas en el TPM del MSM de 500 microestados con el tiempo de retraso de 10 ns establecido como el paso de tiempo de MC. Calcule MFPT⁵² entre cada par de macroestados (Figura 3) mediante el script python en el archivo suplementario 1 python python mfpt_msm3.py.
   2. Calcule el error promedio y estándar del MFPT utilizando el archivo bash en el archivo suplementario 2, escriba:
      sh mfpt_analysis.bash

2. Realización de simulación de grano grueso (CG) para muestrear dinámicas a largo plazo

1. Realice simulaciones CG utilizando el software CafeMol 3.0³⁰. Consulte los ajustes de simulación CG especificados en el archivo de configuración de entrada con una extensión .inp, incluidas las estructuras de entrada, los parámetros de simulación, los archivos de salida, etc. Escriba el siguiente comando en el terminal para ejecutar la simulación CG:
   cafemol XXX.inp
2. Especifique los siguientes bloques en el archivo de entrada, y cada bloque comenzará con la etiqueta < and ending with >>>>.
   1. Establezca el bloque de nombres de archivo (obligatorio) para especificar los directorios de trabajo y la ruta del almacén de archivos de entrada/salida. Escriba lo siguiente para el bloque de nombres de archivo para estas simulaciones:
      <<<< nombres de archivo
      ruta = XXXXX (ruta de trabajo)
      filename = wrky (los nombres de archivo de salida)
      SALIDA psf pdb movie dcd rst
      path_pdb = XXXXX (ruta de entrada de estructura nativa)
      path_ini = XXXXX (ruta de la estructura inicial de entrada)
      path_natinfo = XXXXX (ruta de acceso al archivo de información nativa)
      path_para = XXXXX (ruta de acceso de los archivos de parámetros)
      >>>>
      NOTA: Como el modelo^Go-53 se utiliza en el modelado CG, es decir, la proteína estará sesgada a la conformación nativa, por lo que es necesario establecer la estructura modelada como la conformación nativa. Aquí, la estructura cristalina de entrada se estableció como la conformación nativa.
   2. Establezca el bloque de control de trabajo (obligatorio) para definir el modo de ejecución de las simulaciones. Escriba el siguiente comando:
      <<<< job_cntl
      i_run_mode = 2 (= 2 la simulación de temperatura constante)
      i_simulate_type = 1 (=1 Dinámica de Langevin)
      i_initial_state = 2 (=2 significa que la configuración inicial es configuración nativa)
      >>>>
      Seleccione las simulaciones de dinámica de Langevin de temperatura constante.
   3. Establezca la unidad y el bloque de estado (obligatorio) para definir la información de las estructuras de entrada. Escriba el siguiente comando:
      <<<< unit_and_state
      i_seq_read_style = 1 (=1 significa secuencias leídas desde el archivo PDB)
      i_go_native_read_style = 1 (=1 significa que la estructura nativa es del archivo PDB)
      1 proteína proteína.pdb (unidad y estado molecular_type native_structure)
      ADN 2-3 .pdb (unidad y estado molecular_type native_structure)
      >>>>
      NOTA: Se necesitan los archivos de estructura de entrada iniciales (proteína.pdb y ADN.pdb aquí). Las estructuras están escritas en formato pdb. Aquí se necesitan dos archivos pdb: uno es el archivo de estructura de proteína que contiene las coordenadas del átomo pesado de WRKY (unidad 1), y el otro son las coordenadas del ADN de doble cadena (ds) de 200 pb (unidad 2-3). La proteína se coloca inicialmente a 15 Å del ADN.
   4. Establezca el bloque de función de energía (obligatorio) definido en el bloque de energy_function. Escriba el siguiente comando:
      <<<< energy_function
      LOCAL(1) L_GO
      LOCAL(2-3) L_DNA2
      NLOCAL(1/1) GO EXV ELE
      ADN ELE NLOCAL(2-3/2-3)
      NLOCAL(1/2-3) EXV ELE
      i_use_atom_protein = 0
      i_use_atom_dna = 0
      i_para_from_ninfo = 1
      i_triple_angle_term = 2
      >>>>
      NOTA: En las simulaciones de CG, la proteína es de grano grueso por el modelo^Go-53 con cada aminoácido representado por una partícula CG colocada en su posición Cα. La conformación de la proteína estará sesgada entonces hacia la estructura nativa, o estructura cristalina aquí, bajo el potencial Go (Figura 4A izquierda). El ADN está descrito por el modelo⁵⁴ de 3SPN.2, en el que cada nucleótido está representado por 3 partículas CG S, P, N, que corresponden a azúcar, fosfato y base nitrogenada, respectivamente (Figura 4A derecha). Las interacciones electrostáticas y vdW se consideran entre diferentes cadenas. Las interacciones electrostáticas entre proteína y ADN en la simulación CG se aproximan por el potencial de Debye-Hückel⁵⁵. La energía repulsiva vdW toma la misma forma que en el modelo Go.
   5. Establezca el bloque md_information (obligatorio) para definir la información de simulación. Escriba el siguiente comando:
      <<<< md_information
      n_step_sim = 1
      n_tstep(1) = 500000000
      tstep_size = 0,1
      n_step_save = 1000
      n_step_neighbor = 100
      i_com_zeroing = 0
      i_no_trans_rot = 0
      tempk = 300,0
      n_seed = -1
      >>>>
      El n_tstep es el paso de simulación. Establezca el tstep_size como la duración de cada paso de MD, cada paso de tiempo de CG Cafemol es de aproximadamente 200 fs³⁰, por lo que cada paso de MD aquí es de 200 × 0.1 fs en principio. Actualice la lista de vecinos cada 100 pasos de MD (n_step_neighbor = 100). Ajuste la temperatura de simulación a 300 K. Controle la temperatura empleando el algoritmo Verlet de tipo velocidad para actualizar la estructura de la proteína con el termostato Berendsen⁵⁶.
      NOTA: El n_step_sim es el número de cuenca del potencial basado en el modelo Go, o el número mínimo local de la curva de energía. Un potencial de cuenca múltiple permite que la conformación de la proteína esté sesgada a diferentes conformaciones, de modo que la conformación de la proteína puede cambiar de un mínimo local a otro. Aquí solo se utiliza el modelo Go de cuenca única, lo que significa solo una conformación sesgada (estructura cristalina) para la proteína en las simulaciones. Mientras tanto, dado que no hay interacción de enlace de hidrógeno proteína-ADN, etc. modelado en el contexto CG, los movimientos moleculares se pueden muestrear aún más rápido, es decir, > 10 veces que en las simulaciones atómicas.
   6. Establezca el bloque electrostático (requerido solo cuando se usa la interacción electrostática) ya que la interacción electrostática se considera entre diferentes cadenas, así que use este bloque para definir los parámetros para la interacción electrostática escribiendo:
      <<<< electrostática
      cutoff_ele = 10,0
      ionic_strength = 0,15
      >>>>
      Establezca la longitud de Debye en la interacción electrostática a 10 Å, correspondiente a la condición de la solución. Establezca la fuerza iónica en 0,15 M, como en la condición fisiológica.

Resultados

Deslizamiento acoplado a rotación o paso a paso de 1 pb de WRKY desde la construcción de MSM
Todas las conformaciones de proteínas en el ADN se asignan al movimiento longitudinal X y al ángulo de rotación de la proteína COM a lo largo del ADN (ver Figura 3A). El acoplamiento lineal de estos dos grados indica un paso acoplado a la rotación de la proteína del dominio WRKY en el ADN. Las conformaciones se pueden agrupar en 3 macroestados (S1, S2 y S3) en el MSM. El p...

Discusión

Este trabajo aborda cómo realizar simulaciones computacionales basadas en la estructura y muestreos para revelar un factor de transcripción o proteína TF que se mueve a lo largo del ADN, no solo en el detalle atómico del paso, sino también en la difusión procesiva, que es esencial para la difusión facilitada de TF en la búsqueda de objetivos de ADN. Para hacer eso, primero se construyó el modelo de estado de Markov o MSM de una pequeña proteína de dominio TF WRKY que avanza para 1-pb a lo largo del ADN poli-A ...

Materiales

Name	Company	Catalog Number	Comments
CafeMol	Kyoto University		coarse-grained (CG) simulations
GROMACS	University of Groningen Royal Institute of Technology Uppsala University		molecular dynamics simulations software
Matlab	MathWorks		Numerical calculation software
MSMbuilder	Stanford University		build MSM
VMD	UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN		molecular visualization program