Simulação baseada em estrutura e amostragem de movimentos de proteína do fator de transcrição ao longo do DNA de pisando em escala atômica para difusão grosseira

Resumo

O objetivo deste protocolo é revelar a dinâmica estrutural da difusão unidimensional de proteína ao longo do DNA, usando um fator de transcrição vegetal proteína de domínio WRKY como um sistema exemplar. Para isso, foram implementadas simulações de dinâmica molecular atomística e grosseira, juntamente com extensas amostras computacionais.

Resumo

O deslizamento unidimensional (1-D) da proteína fator de transcrição (TF) ao longo do DNA é essencial para a difusão facilitada do TF para localizar o local de DNA alvo para regulação genética. Detectar a resolução do par de bases (bp) do TF deslizando ou pisando no DNA ainda é experimentalmente desafiador. Recentemente realizamos simulações de dinâmica molecular de todos os átomos (MD) capturando um passo espontâneo de 1 bp de uma pequena proteína TF de domínio WRKY ao longo do DNA. Com base no caminho de 10 μs WRKY obtido a partir de tais simulações, o protocolo aqui mostra como realizar amostras conformais mais extensas dos sistemas TF-DNA, construindo o modelo de estado markov (MSM) para a pisada de proteína de 1 bp, com vários números de micro e macro-estados testados para a construção do MSM. A fim de examinar a busca difusiva 1D processiva da proteína TF ao longo do DNA com base estrutural, o protocolo mostra ainda como realizar simulações de MD de grãos grosseiros (CG) para amostrar dinâmicas de escala de longo prazo do sistema. Tais modelagem e simulações de CG são particularmente úteis para revelar os impactos eletrostáticos de DNA proteico nos movimentos difusivos processivos da proteína TF acima de dezenas de microssegundos, em comparação com sub-microsegundos a movimentos de pisando proteicos microsegundos revelados a partir das simulações de todos os átomos.

Introdução

Fatores de transcrição (TF) buscam o DNA alvo para vincular e regular a transcrição genética e as atividades relacionadas¹. Além da difusão tridimensional (3D), a difusão facilitada de TF tem sido sugerida como essencial para a busca de DNA alvo, na qual as proteínas também podem deslizar ou saltar ao longo do DNA unidimensional (1D) ou saltar com transferência intersegmental no DNA 2,3,4,5,6,7.

Em um estudo recente, realizamos dezenas de microssegundos (μs) de todas as simulações de dinâmica molecular de equilíbrio átomo (MD) em uma planta TF - a proteína de domínio WRKY no DNA⁸. Um passo completo de 1 bp de WRKY em DNA poli-A dentro de microssegundos foi capturado. Os movimentos da proteína ao longo da dinâmica de quebra de cadeias de DNA e de hidrogênio (HBs) foram observados. Embora tal trajetória represente um caminho amostrado, uma paisagem global de intensificação de proteínas ainda é a falta. Aqui, mostramos como expandir as amostras computacionais ao redor do caminho de avanço proteico inicialmente capturado com o modelo de estado markov construído (MSM), que foram amplamente implementados para simular uma variedade de sistemas biomoleculares envolvendo mudanças conformais substanciais e separação em escala de tempo 9,10,11,12,13,14,15,16^, 17,18,19. O objetivo é revelar o conjunto conformacional e os estados meta-estáveis da difusão da proteína TF ao longo do DNA para um passo cíclico.

Enquanto a simulação de MD acima revela a resolução atômica dos movimentos proteicos para 1 bp no DNA, a dinâmica estrutural da difusão processiva de longa data do TF ao longo do DNA na mesma alta resolução dificilmente é acessível. A realização de simulações de MD de grãos grosseiros (CG) ao nível de resíduo é tecnicamente acessível. A escala de tempo de simulação cg pode ser efetivamente estendida para dezenas ou centenas de vezes mais do que as simulações atômicas 20,21,22,23,24,25,26,27,28,29. Aqui, mostramos as simulações de CG conduzidas pela implementação do software CafeMol desenvolvido pelo laboratório Takada³⁰.

No protocolo atual, apresentamos as simulações atômicas da proteína de domínio WRKY ao longo do DNA poli-A e da construção do MSM primeiro, que se concentram na amostragem dos movimentos de intensificação da proteína por apenas 1 bp ao longo do DNA. Em seguida, apresentamos a modelagem CG e simulações do mesmo sistema proteína-DNA, que estendem a amostragem computacional à difusão processiva de proteína sobre dezenas de bps ao longo do DNA.

Aqui, usamos o software GROMACS^31,32,33 para realizar simulações de MD e MSMbuilder³⁴ para construir o MSM para instantâneos conformacionais amostrados, bem como para usar o VMD³⁵ para visualizar as biomoléculas. O protocolo exige que o usuário seja capaz de instalar e implementar o software acima. A instalação e implementação do software CafeMol³⁰ é então necessária para a realização das simulações de CG MD. Outras análises das trajetórias e visualização também são realizadas em VMD.

Protocolo

1. Construção do modelo de estado markov (MSM) a partir de simulações atômicas de MD

1. Caminho de passo de proteína espontânea e coleta de estruturas iniciais
   1. Use uma trajetória de 10 μs md de 10 μs de todos os átomos⁸ para extrair 10000 quadros uniformemente de um caminho de 1 bp "para a frente" (ou seja, um quadro para cada nanossegundo). O número total de quadros precisa ser suficientemente grande para incluir todas as conformações representativas.
   2. Prepare o caminho de transição com 10000 quadros em VMD clicando em Arquivo > Salve coordenadas, digite proteína ou nucleic na caixa de átomos selecionados e escolha quadros na caixa Quadros, clique em Salvar para obter os quadros necessários.
      NOTA: Uma trajetória de simulação de MD de 10 μs de todos os átomos (chamada "trajetória de passo para frente" aqui) para WRKY pisar a distância de 1 bp em um DNA poli-A homogêneo^de 34 bps foi usado como o caminho inicial para lançar novas amostras conformais. Observe que na maioria das práticas, no entanto, um caminho inicial é construído, realizando simulações de MD direcionadas ou direcionadas, ou implementando métodos gerais de geração de caminhos, etc.36,37,38,39.
   3. Alinhe o longo eixo do DNA de referência (da estrutura cristalina) ao eixo x, e defina o centro inicial de massa (COM) do DNA completo de 34 bps na origem do espaço de coordenadas para a conveniência de uma análise de dados mais aprofundada. Para fazer isso, clique em Extensões > Tk Console em VMD e digite na janela de comando do console Tk:
      rotação de fonte.tcl
      O script tcl pode ser encontrado no Arquivo Complementar 3.
   4. Em seguida, calcule a distância média-radicular (RMSD) da espinha dorsal da proteína alinhando o DNA central de 10 bp (A 14 a 23 e T 14' a 23') a partir da estrutura cristalina⁴⁰, e o RMSD representa medidas geométricas dos sistemas (ver Figura 1A). Faça isso clicando em VMD > Extensões > Análise > ferramenta de trajetória RMSD e digite nucleic e resíduo 14 a 23 e 46 a 55 na caixa de seleção de átomos, clique em Alinhar e, em seguida, caixa RMSD para calcular os valores RMSD.
   5. Calcule o grau de rotação da proteína em torno do DNA Φ(t) no plano y-z no MATLAB digitando o comando
      rad2deg(atan(z/y))
      com o posicionamento angular inicial definido como Φ(0)=0, como realizado anteriormente⁸.
   6. Digite o seguinte comando no MATLAB⁴¹ para usar os métodos k-means 42,43,44 e classificar as estruturas 10000 em 25 clusters digitando:
      [idx, C]=kmeans( X, 25)
      aqui X é uma matriz 2D de RMSD e ângulo rotacional de WRKY no DNA. Reúna as estruturas desses 25 centros de cluster para mais simulações de MD.
      NOTA: Uma vez que a proteína RMSD amostrada em relação ao DNA cobre uma faixa de cerca de 25 Å, escolhemos 25 clusters para ter um cluster por angstrom.
2. Realização da^1ª rodada de simulações de MD e as configurações de simulação
   1. Construa sistemas atomísticos para as 25 estruturas usando o software GROMACS 5.1.2³² sob o campo de força parmbsc1⁴⁵ e usando o arquivo buildsystem.sh do Arquivo Suplementar 2 em shell.
   2. Realize simulações de MD de 60 ns para estes 25 sistemas sob conjunto NPT com uma etapa de tempo de 2 fs digitando o seguinte comando em shell:
      gmx_mpi grompp -f md.mdp -c npt.gro -p topol.top -o md.tpr
      gmx_mpi mdrun -deffnm md
3. Agrupando o 1^St trajetórias de MD redondas
   1. Remova os primeiros 10 ns de cada trajetória de simulação digitando em shell:
      gmx_mpi trjcat -f md.xtc -b 10000 -e 6000000 -o newtraj.xtc
      e coletar conformações das trajetórias de 25 × 50 ns para agrupamento para preparar as estruturas de entrada para as amostras mais extensas subsequentes (simulações de MD^{da 2ª} rodada).
      NOTA: Para reduzir o impacto do caminho inicial e permitir o equilíbrio local, foram removidos 10 ns do período inicial de simulações.
   2. Escolha pares de distância entre proteína e DNA como parâmetros de entrada para a análise de componentes independentes do tempo (tICA)46,47,48 projeção. Use o comando make_ndx no GROMACS para fazer isso:
      gmx_mpi make_ndx -f entrada.pdb -o índice.ndx
      NOTA: Aqui, os átomos de proteína CA e os átomos pesados (NH1, NH2, OH, NZ, NE2, ND2) de resíduo Y119, K122, Foram selecionados K125, R131, Y133, Q146, K144, R135, W116, R117, Y134, K118, Q121 que podem formar ligações de hidrogênio (HBs) com o nucleotídeo de DNA, que combinam com os átomos O1P O2P e N6 do nucleotídeo de DNA (A14-20, T19-23). Os aminoácidos selecionados podem formar HBs estáveis ou pontes de sal com DNA.
   3. Copie o índice de átomo acima selecionado do arquivo index.ndx para um novo arquivo de texto (índice.dat). Obtenha as informações do par entre esses átomos pelo script python do Arquivo Suplementar 1 generate_atom_indices.py e digite:
      índice de generate_atom_indices.py python2.6.dat > AtomIndices.txt
      Isso gera os 415 pares de distância entre proteína e DNA.
   4. Calcule os pares de 415 distâncias de cada trajetória digitando o seguinte comando na janela de comando MSMbuilder:
      msmb AtomPairsFeaturizer -out pair_features --pair_indices AtomIndices.txt --principais referências.pdb --trjs "trajetórias/*.xtc" --transformadas pair_features --stride 5
   5. Conduzir o tICA para reduzir a dimensão dos dados nos dois primeiros componentes independentes do tempo (tICs) ou vetores digitando:
      msmb tICA -i .. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gama 0.05 -t tica_results.h5
      NOTA: o tICA é um método de redução de dimensões que calcula o eigenvalue da matriz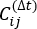 de correlação com atraso de tempo para determinar os graus mais lentos de liberdade do sistema de simulação pela equação: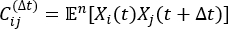
      
      onde X_i(t) é o valor da coordenada de reação i-th no momento t, e X_j(t+Δt) é o valor da coordenada de reação j-th no momento t+Δt.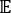 é o valor de expectativa do produto das trajetórias de simulação geral X_i(t) e X_j(t + Δt). As direções ao longo dos graus de liberdade relaxantes mais lentos correspondem aos maiores valores eigen da matriz 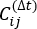de correlação acima de tempo. Aqui, 2 tICs parecem ser um conjunto mínimo para diferenciar três macroestações em nossa construção MSM (abordada posteriormente). Pode-se também calcular a pontuação de⁴⁹% do quociente de matriz generalizada rayleigh (GMRQ), por exemplo, para explorar um conjunto ideal de componentes a serem usados.
   6. Use o comando no MSMbuilder para agrupar os conjuntos de dados projetados em 100 clusters pelo método K-center^43,44 (ver Figura 1B):
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 100.
      Selecione a estrutura central de cada cluster como a estrutura inicial para a^2ª rodada de simulações de MD. Manter as informações de simulação das 100 estruturas simuladas, incluindo posições, temperaturas, pressões, etc., exceto pelas velocidades.
      NOTA: Após a primeira rodada de 25 simulações, a memória do caminho inicial foi reduzida, por isso geramos mais clusters, por exemplo, 100 clusters, no segundo turno, para expandir substancialmente as amostrais conformais.
4. Conduzindo as extensas simulações de MD da^2ª rodada
   1. Realize simulações de MD de 60 ns a partir dessas 100 estruturas iniciais depois de impor velocidades iniciais aleatórias em todos os átomos. Adicione as velocidades iniciais aleatórias ligando a geração de velocidade no arquivo mdp, ou seja, alterando o arquivo md.mdp gen_vel = não para gen_vel = sim.
   2. Remova os primeiros 10 ns de cada simulação conforme descrito na etapa 1.3.1, colete 2.500.000 instantâneos das trajetórias de 100 × 50 ns uniformemente para construir o MSM.
      NOTA: Note-se que na construção de macroestações posteriores, um pequeno número de estados fora do caminho com uma população particularmente baixa (~0,2%, na parte inferior do avião X-Φ) foram encontrados. Esses estados fora do caminho são classificados como um macroestado quando o número total de macroestações é definido como 3 a 6 (Figura 2B). Uma vez que uma macroestado populacional tão baixa inclui apenas 3 trajetórias, que foram removidas no final, os resultados mostrados neste protocolo foram obtidos de fato de 97 × trajetórias de 50 ns, com um total de 2.425.000 quadros ou instantâneos.
5. Agrupando as trajetórias de MD^{da 2ª} rodada
   1. Conduzir tICA para as trajetórias da^2ª rodada, como feito anteriormente. Digite MSMbuilder:
      msmb tICA -i .. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gama 0.05 -t tica_results.h5
   2. Calcule a escala de tempo implícita para validar parâmetros para o tempo de atraso de correlação Δt e números de microestados (ver Figura 1C),
      
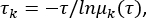
      onde τ representa o tempo de atraso utilizado para a construção da matriz de probabilidade de transição (TPM); μ_k(τ) representa o kth eigenvalue do TPM sob um tempo de atraso de τ. Use o script python do Arquivo Suplementar 1 para este BuildMSMsAsVaryLagTime.py python -d .. / -f .. /trajlist_num -i 50 -m 1000 -t 10 -n 20 -s 500.
   3. Varie o número de τ e microestados de atraso alterando os parâmetros utilizados acima:
      píton BuildMSMsAsVaryLagTime.py -d .. / -f .. /trajlist_num -i 50 -m 1000 -t 5 10 20 30 40 -n 20 -s 20 200 400 500 800 2000
      NOTA: O sistema é considerado markovian quando as curvas de escala de tempo implícita começam a nivelar com a separação em escala de tempo. Em seguida, escolha o Dt como o tempo de atraso de correlação, e o tempo de atraso onde a escala de tempo implícita começa a nivelar para construir MSM.
   4. Assim, escolha um número comparativamente grande (mas não muito grande) de estados, N = 500, e um tempo de atraso de correlação relativamente curto Δt =10 ns. O tempo de defasagem foi encontrado para ser τ =10 ns para construir MSM.
   5. Classifique as conformações em 500 clusters (ver Figura 1D) usando o comando:
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 500
6. Construção msm
   1. Coloque os 500 microestados em 3-6 macroestáditos para descobrir o número de macroestações que melhor se adequam de acordo com o algoritmo PCCA+⁵⁰ em MSMbuilder, usando o script python em msm_lumping_usingPCCAplus.py python suplementar. Identifique uma rede cinética reduzida de modelos para as mudanças conformais mais essenciais das biomoléculas, construindo um pequeno número de macroestados, ou seja, sobre a fixação cineticamente de centenas de microestados, conforme descrito abaixo de^17,51.
   2. Mapear as conformações de alta dimensão ao X (movimento proteico ao longo do eixo longo do DNA) e ângulo rotacional da proteína ao longo do DNA para cada macroestado como descrito na etapa 1.1.3 e 1.1.4 (por exemplo, nenhum estado com população muito baixa < 1%; ver Figura 2C). Em seguida, encontre as 3 macroestações que melhor representam o sistema (Figura 1E) . Veja a Figura 2D para obter instantâneos do movimento da proteína ao longo do DNA e do ângulo de rotação de proteínas em torno do DNA.
      NOTA: Em trabalhos anteriores gerando a proteína espontânea de 10 μs para a frente, também realizamos simulações de MD de equilíbrio de 5 x 4 μs para expandir moderadamente as amostras. Mostramos o mapeamento do caminho original para a frente (ver Figura 2A à esquerda) e outras trajetórias amostrais de 4-μs no caminho a seguir realizado anteriormente (ver Figura 2A à direita)⁸. O mapeamento das trajetórias originais de 100 × 50 ns (ver Figura 2B à esquerda)⁸ e as trajetórias de 97 × 50 ns utilizadas neste trabalho são mostradas (ver Figura 2B à direita).
7. Cálculo dos tempos médios de primeira passagem (MFPT)
   1. Realize cinco trajetórias de Monte Carlo (MC) de 10 ms com base no TPM do MSM de 500 microestaduais com o tempo de atraso de 10 ns definido como o passo de tempo de MC. Calcule MFPT⁵² entre cada par de macroestações (Figura 3) pelo script python em Arquivo Suplementar 1 python mfpt_msm3.py.
   2. Calcule o erro médio e padrão do MFPT usando o arquivo bash no Arquivo Suplementar 2, digite:
      sh mfpt_analysis.bash

2. Realização de simulação de grãos grosseiros (CG) para amostrar dinâmicas de longo prazo

1. Realize uma simulação CG usando o software CafeMol 3.0³⁰. Consulte as configurações de simulação CG especificadas no arquivo de configuração de entrada com uma extensão .inp, incluindo estruturas de entrada, parâmetros de simulação, arquivos de saída, etc. Digite o seguinte comando no terminal para executar a simulação cg:
   cafemol XXX.inp
2. Especifique os seguintes blocos no arquivo de entrada, com cada bloco começando com a >>> de rótulo < and ending with >.
   1. Defina o bloco de nomes de arquivos (necessário) para especificar os diretórios de trabalho e o caminho da loja de arquivos de entrada/saída. Digite a seguir para o bloco de nomes de arquivos para essas simulações:
      <<<< nomes de arquivos
      caminho = XXXXX (caminho de trabalho)
      nome de arquivo = wrky (os nomes dos arquivos de saída)
      SAÍDA psf pdb filme dcd rst
      path_pdb = XXXXX (caminho da estrutura nativa de entrada)
      path_ini = XXXXX (caminho da estrutura inicial de entrada)
      path_natinfo = XXXXX (caminho de arquivo de informações nativas)
      path_para = XXXXX (caminho de arquivos de parâmetros)
      >>>>
      NOTA: Como o Go-model⁵³ é utilizado na modelagem CG, ou seja, a proteína será tendenciosa à conformação nativa, por isso é preciso definir a estrutura modelada como a conformação nativa. Aqui, a estrutura de cristal de entrada foi definida como a conformação nativa.
   2. Defina o bloco de controle de trabalho (necessário) para definir o modo de execução das simulações. Digite o seguinte comando:
      <<<< job_cntl
      i_run_mode = 2 (= 2 a simulação de temperatura constante)
      i_simulate_type = 1 (=1 dinâmica langevina)
      i_initial_state = 2 (=2 significa que a configuração inicial é configuração nativa)
      >>>>
      Selecione as simulações de dinâmica de Langevin de temperatura constante.
   3. Defina a unidade e o bloco estadual (necessários) para definir as informações para estruturas de entrada. Digite o seguinte comando:
      <<<< unit_and_state
      i_seq_read_style = 1 (=1 significa sequências de leitura do arquivo PDB)
      i_go_native_read_style = 1 (=1 significa que a estrutura nativa é de arquivo PDB)
      1 proteína.pdb (molecular_type native_structure unit&state)
      DNA 2-3.pdb (molecular_type native_structure unit&state)
      >>>>
      NOTA: Os arquivos iniciais da estrutura de entrada (proteína.pdb e DNA.pdb aqui) são necessários. As estruturas estão escritas no formato pdb. Dois arquivos pdb são necessários aqui: um é o arquivo de estrutura proteica contendo as coordenadas pesadas do átomo de WRKY (unidade 1), e o outro são as coordenadas de DNA de 200 bps de dupla-stranded (ds) (unidade 2-3). A proteína é inicialmente colocada a 15 Å de distância do DNA.
   4. Defina o bloco de função de energia (necessário) definido no bloco energy_function. Digite o seguinte comando:
      <<<< energy_function
      LOCAL(1) L_GO
      LOCAL (2-3) L_DNA2
      NLOCAL(1/1) GO EXV ELE
      DNA ELE NLOCAL (2-3/2-3)
      NLOCAL(1/2-3) EXV ELE
      i_use_atom_protein = 0
      i_use_atom_dna = 0
      i_para_from_ninfo = 1
      i_triple_angle_term = 2
      >>>>
      NOTA: Nas simulações cg, a proteína é grosseira pelo Modelo Go⁵³ com cada aminoácido representado por uma partícula CG colocada em sua posição Cα. A conformação proteica será tendenciosa em seguida, para a estrutura nativa, ou estrutura cristalina aqui, sob o potencial Go (Figura 4A esquerda). O DNA é descrito pelo modelo 3SPN.2⁵⁴, no qual cada nucleotídeo é representado por 3 partículas CG S, P, N, que correspondem ao açúcar, fosfato e base nitrogenada, respectivamente (Figura 4A à direita). As interações eletrostáticas e vdW são consideradas entre diferentes cadeias. As interações eletrostáticas entre proteína e DNA na simulação CG são aproximadas pelo potencial Debye-Hückel⁵⁵. A energia repulsiva vdW toma a mesma forma que no modelo Go.
   5. Defina o bloco de md_information (necessário) para definir as informações de simulação. Digite o seguinte comando:
      <<<< md_information
      n_step_sim = 1
      n_tstep(1) = 5000000000
      tstep_size = 0,1
      n_step_save = 1000
      n_step_neighbor = 100
      i_com_zeroing = 0
      i_no_trans_rot = 0
      tempk = 300,0
      n_seed = -1
      >>>>
      O n_tstep é a etapa de simulação. Defina o tstep_size como o tempo de cada etapa MD, cada passo de tempo do CG Cafemol é de cerca de 200 fs³⁰, então cada passo MD aqui é de 200 × 0,1 fs em princípio. Atualize a lista de vizinhos a cada 100 passos de MD (n_step_neighbor = 100). Defina a temperatura da simulação para 300 K. Controle a temperatura empregando o algoritmo verlet tipo velocidade para atualizar a estrutura proteica com o termostato Berendsen⁵⁶.
      NOTA: O n_step_sim é o número de bacia do potencial baseado no modelo Go, ou o número mínimo local da curva de energia. Um potencial de várias bacias permite que a conformação proteica tendenciosa a diferentes conformações de modo que a conformação proteica possa mudar de um mínimo local para outro. Aqui é utilizado apenas o modelo Go de bacia única, o que significa apenas uma conformação tendenciosa (estrutura cristalina) para proteína nas simulações. Enquanto isso, como não há interação de ligação proteína-DNA hidrogênio, etc. modelado no contexto CG, os movimentos moleculares podem ser amostrados ainda mais rápido, ou seja, > 10 vezes do que nas simulações atômicas.
   6. Definir o bloco eletrostático (necessário apenas quando a interação eletrostática é usada) como a interação eletrostática é considerada entre diferentes cadeias, por isso use este bloco para definir os parâmetros para interação eletrostática digitando:
      <<<< eletrostático
      cutoff_ele = 10,0
      ionic_strength = 0,15
      >>>>
      Defina o comprimento de Debye na interação eletrostática para 10 Å, correspondendo à condição da solução. Coloque a força iônica em 0,15 M, como na condição fisiológica.

Resultados

Deslizamento acoplado de rotação ou 1 bp de piso de WRKY da construção msm
Todas as conformações proteicas no DNA são mapeadas para o movimento longitudinal X e ângulo de rotação da proteína COM ao longo do DNA (ver Figura 3A). O acoplamento linear desses dois graus indica um passo acoplado de rotação da proteína de domínio WRKY no DNA. As conformações podem ser agrupadas em 3 macroestações (S1, S2 e S3) no MSM. O passo para a frente do WRKY segue entã...

Discussão

Este trabalho aborda como realizar simulações computacionais baseadas em estrutura e amostras para revelar um fator de transcrição ou proteína TF movendo-se ao longo do DNA, não apenas no detalhe atômico da pisada, mas também na difusão processiva, que é essencial para a difusão facilitada de TF na busca de alvos de DNA. Para isso, o modelo de estado markov ou MSM de uma pequena proteína de domínio TF WRKY pisando para 1-bp ao longo de DNA poli-A homogêneo foi construído pela primeira vez, de modo que um c...

Materiais

Name	Company	Catalog Number	Comments
CafeMol	Kyoto University		coarse-grained (CG) simulations
GROMACS	University of Groningen Royal Institute of Technology Uppsala University		molecular dynamics simulations software
Matlab	MathWorks		Numerical calculation software
MSMbuilder	Stanford University		build MSM
VMD	UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN		molecular visualization program