JoVE Logo
著者
お問い合わせ

サインイン

このコンテンツを視聴するには、JoVE 購読が必要です。 サインイン又は無料トライアルを申し込む。

この記事について

  • 要約
  • 要約
  • 概要
  • プロトコル
  • 結果
  • ディスカッション
  • 開示事項
  • 謝辞
  • 資料
  • 参考文献
  • 転載および許可

要約

このプロトコールの目標は、植物転写因子WRKYドメインタンパク質を例示的な系として用いて、DNAに沿ったタンパク質の1次元拡散の構造ダイナミクスを明らかにすることである。これを行うために、原子論的および粗粒度の分子動力学シミュレーションと広範な計算サンプリングの両方が実装されています。

要約

DNAに沿った転写因子(TF)タンパク質の1次元(1-D)スライディングは、遺伝子調節のために標的DNA部位を位置特定するためのTFの拡散を促進するために不可欠である。DNAをスライドまたは踏むTFの塩基対(bp)分解能を検出することは、依然として実験的に困難です。我々は最近、DNAに沿った小さなWRKYドメインTFタンパク質の自発的な1-bpステッピングを捕捉する全原子分子動力学(MD)シミュレーションを行った。このようなシミュレーションから得られた10μsのWRKYステッピング経路に基づいて、ここでのプロトコルは、1-bpタンパク質ステッピングのためのマルコフ状態モデル(MSM)を構築し、MSM構築のために様々な数のミクロおよびマクロ状態をテストすることによって、TF-DNAシステムのより広範な立体構造サンプリングを行う方法を示す。DNAに沿ったTFタンパク質のプロセス的1次元拡散探索を構造的基礎とともに調べるために、このプロトコルはさらに、システムの長期スケールのダイナミクスをサンプリングするために粗粒(CG)MDシミュレーションを行う方法を示す。このようなCGモデリングおよびシミュレーションは、全原子シミュレーションから明らかにされたサブマイクロ秒からマイクロ秒のタンパク質ステッピング運動と比較して、数十マイクロ秒を超えるTFタンパク質のプロセス拡散運動に対するタンパク質-DNA静電的影響を明らかにするのに特に有用である。

概要

転写因子(TF)は、遺伝子転写および関連活性を結合および調節する標的DNAを探索する1.3次元(3D)拡散とは別に、TFの促進された拡散は、タンパク質が1次元(1D)DNAに沿ってスライドまたはホップしたり、DNA上のセグメント間転写でジャンプしたりすることができる標的DNA探索に不可欠であることが示唆されている2、3、4、5、6、7。

最近の研究では、DNA上のWRKYドメインタンパク質である植物TFについて、数十マイクロ秒(μs)の全原子平衡分子動力学(MD)シミュレーションを実施しました8。マイクロ秒以内にポリA DNA上のWRKYの完全な1-bpステッピングがキャプチャされました。DNA溝に沿ったタンパク質の動きと水素結合(HB)の破壊・改質ダイナミクスが観察されている。このような軌道は1つのサンプリングされた経路を表しますが、全体的なタンパク質ステッピングランドスケープはまだ欠けています。ここでは、実質的な立体構造変化および時間スケール分離9、10、11、12、13、14、15、16を含む様々な生体分子系をシミュレートするために広く実装されている構築されたマルコフ状態モデル(MSM)を用いて、最初に捕捉されたタンパク質ステッピング経路の周りの計算サンプリングを拡張する方法を示し、17,18,19。その目的は、1つの環状ステップのためのDNAに沿ったTFタンパク質拡散の立体構造アンサンブルおよび準安定状態を明らかにすることである。

上記のMDシミュレーションは、DNA上の1 bpのタンパク質移動の原子分解能を明らかにしているが、同じ高分解能でのDNAに沿ったTFの長時間のプロセス拡散の構造ダイナミクスはほとんどアクセスできない。しかし、残留物レベルで粗粒度(CG)MDシミュレーションを実施することは、技術的には親しみやすいことです。CGシミュレーションの時間スケールは、原子シミュレーション20、21、22、23、24、25、26、27、28、29よりも数十倍または数百倍の長さに効果的に拡張することができる。ここでは、高田研究室30が開発したCafeMolソフトウェアを実装して行ったCGシミュレーションを紹介します。

現在のプロトコルでは、ポリA DNAに沿ったWRKYドメインタンパク質の原子シミュレーションと、DNAに沿ったわずか1 bpのタンパク質ステッピング運動のサンプリングに焦点を当てたMSM構築を最初に提示する。次に、同じタンパク質-DNA系のCGモデリングとシミュレーションを提示し、計算サンプリングをDNAに沿って数十bpsにわたるタンパク質プロセス拡散に拡張します。

ここでは、GROMACS 31,32,33ソフトウェアを使用してMDシミュレーションを行い、MSMbuilder 34を使用してサンプリングされた立体構造スナップショット用のMSMを構築し、VMD 35を使用して生体分子を視覚化します。このプロトコルでは、ユーザーが上記のソフトウェアをインストールして実装できる必要があります。CG MDシミュレーションを行うには、CafeMol30ソフトウェアのインストールと実装が必要です。軌道のさらなる分析と視覚化もVMDで行われます。

プロトコル

1. 原子MDシミュレーションによるマルコフ状態モデル(MSM)の構築

  1. 自発的なタンパク質ステッピング経路と初期構造収集
    1. 以前に取得した10μsの全原子MD軌道8 を使用して、「順方向」の1bpステッピングパス(すなわち、ナノ秒ごとに1フレーム)から10000フレームを均等に抽出する。フレームの総数は、すべての代表的な立体配座を含むのに十分な大きさである必要があります。
    2. VMDで10000フレームの遷移パスを準備する には、[ファイル]>[座標を保存し、選択した原子にタンパク質または核酸を入力し]ボックスに入力し、[フレーム]ボックスで[ 保存 ]をクリックして必要なフレームを取得します。
      注:34 bpの均質なポリA DNA8上のWRKYステッピング1-bp距離について、以前に得られた10μsの全原子MDシミュレーション軌道(ここでは「順方向ステッピング軌道」と呼ばれる)を、さらなる立体構造サンプリングを開始するための初期経路として使用した。ただし、ほとんどのプラクティスでは、ステアリングまたはターゲットを絞ったMDシミュレーションを実行したり、一般的なパス生成方法などを実装することによって、初期パスが構築されることに注意してください36,37,38,39。
    3. 参照DNAの長軸(結晶構造から)をx軸に揃え、完全な34bpDNAの初期質量中心(COM)を座標空間の原点に設定して、さらなるデータ解析を容易にします。これを行うには、VMD の Tk コンソール >拡張機能をクリックし、Tk コンソール のコマンド ウィンドウに次のように入力します。
      ソース rotate.tcl
      tcl スクリプトは 補足ファイル 3 にあります。
    4. 次に、中央10 bp DNA(A14〜23およびT14'〜23')を結晶構造40からのものに整列させることによってタンパク質骨格の二乗平均平方根距離(RMSD)を計算し、RMSDは系の幾何学的測定値を表す( 図1A参照)。これを行うには、 RMSD 軌道ツール> VMD > Extensions > Analysis をクリックし、原子選択ボックスに核酸と残基 14 ~ 23 および 46 ~ 55 と入力し、[ 整列 ] をクリックしてから RMSD ボックスをクリックして RMSD 値を計算します。
    5. コマンドを入力して、MATLABのy-z平面上のDNA Θ(t)の周りのタンパク質の回転度を計算します。
      rad2deg(atan(z/y))
      初期角度位置決めは、以前に実施したようにΘ(0)=0として定義される8。
    6. MATLAB41 に次のコマンドを入力して、K-means メソッド42,43,44 を使用し、次のように入力して 10000 個の構造体を 25 個のクラスターに分類します。
      [idx, C]=kmeans( X, 25)
      ここで X は、DNA上のRMSDとWRKYの回転角の2D行列である。これらの25のクラスタ中心の構造を収集して、さらなるMDシミュレーションを行います。
      注:DNAに対してサンプリングされたタンパク質RMSDは約25オングストロームの範囲をカバーするため、オングストロームごとに1つのクラスターを持つように25個のクラスターを選択します。
  2. 第1ラウンドのMDシミュレーションとシミュレーション設定の実施
    1. parmbsc1 力場45 の下で GROMACS 5.1.2 ソフトウェア32 を使用し、シェルの補足ファイル 2 の buildsystem.sh ファイルを使用して、25 の構造の原子論的システムを構築します。
    2. シェルで次のコマンドを入力して、NPT アンサンブルの下でこれらの 25 システムの 60 ns MD シミュレーションを 2 fs の時間ステップで実行します。
      gmx_mpi grompp -f md.mdp -c npt.gro -p topol.top -o md.tpr
      gmx_mpi mdrun -deffnm md
  3. 1のクラスタリング聖 ラウンドMD軌道
    1. 各シミュレーション軌道の最初の 10 ns を削除するには、シェルに次のように入力します。
      gmx_mpi trjcat -f md.xtc -b 10000 -e 600000 -o newtraj.xtc
      クラスタリングのために25 ns×50 nsの軌道から立体構造を収集し、その後のより広範なサンプリング(2回目の MDシミュレーション)のために入力構造を準備します。
      注: 初期パスからの影響を軽減し、局所的な平衡化を可能にするために、シミュレーションの初期期間の 10 ns が削除されました。
    2. 時間非依存成分分析(tICA)46,47,48投影の入力パラメータとしてタンパク質とDNAの間の距離ペアを選択します。これを行うには、GROMACS で make_ndx コマンドを使用します。
      gmx_mpi make_ndx -f 入力.pdb -o index.ndx
      注:ここでは、DNAヌクレオチドと水素結合(HB)を形成できるタンパク質CA原子および残基Y119、K122、K125、R131、Y133、Q146、K144、R135、W116、R117、Y134、K118、Q121の重原子(NH1、NH2、OH、NZ、NE2、ND2)を選択し、DNAヌクレオチドのO1P O2PおよびN6原子と対をなすもの(A14-20、 T19-23)。選択されたアミノ酸は、DNAと安定なHBまたは塩架橋を形成することができる。
    3. 上記の選択したアトム インデックスを index.ndx ファイルから新しいテキスト ファイル (index.dat) にコピーします。 補足ファイル1 のgenerate_atom_indices.pyからPythonスクリプトによってこれらの原子間のペア情報を取得し、次のように入力します。
      python2.6 generate_atom_indices.py index.dat > AtomIndices.txt
      これにより、タンパク質とDNAの間に415の距離ペアが生成されます。
    4. MSMbuilder コマンド ウィンドウで次のコマンドを入力して、すべての軌道から 415 の距離ペアを計算します。
      msmb AtomPairsFeaturizer -out pair_features --pair_indices AtomIndices.txt --top references.pdb --trjs "trajectories/*.xtc" --transformed pair_features --stride 5
    5. tICAを実行して、次のように入力して、最初の2つの時間非依存コンポーネント(tIC)またはベクトルにデータの次元を縮小します。
      msmb tICA -i ../tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --γ 0.05 -t tica_results.h5
      注:tICAは、時間時間差相関行列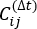 figure-protocol-4077 の固有値を計算し、シミュレーションシステムの最も遅い緩和自由度を次の式で決定する次元縮小方法です。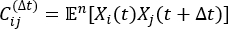
      figure-protocol-4197
      ここで、XI(t)は時刻tにおけるi番目の反応座標の値であり、Xj(t+Δt)は時刻t+Δtにおけるj番目の反応座標の値である。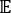figure-protocol-4425は、XI(t) と Xj(t + Δ t) 全体のシミュレーション軌道の積の期待値です。最も遅い緩和自由度に沿った方向は、上記の時間時間差相関行列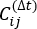figure-protocol-4631の最大の固有値に対応します。ここで、2つのtICは、MSM構築時に3つのマクロ状態を区別するための最小セットのようです(後述)。一般化行列レイリー商(GMRQ)スコア49を計算して、例えば、使用される成分の最適なセットを探索することもできる。
    6. MSMbuilder のコマンドを使用して、K センター43,44 メソッドによって投影データセットを 100 個のクラスターにクラスター化します (図 1B を参照)。
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 100.
      各クラスタの中心構造を、第 2 ラウンドの MD シミュレーションの初期構造として選択します。速度を除いて、位置、温度、圧力などを含むシミュレートされた100の構造のシミュレーション情報を維持します。
      注: 25 回のシミュレーションの最初のラウンドの後、初期パスのメモリが削減されたため、コンフォメーション サンプリングを大幅に拡張するために、2 回目のラウンドでより多くのクラスター (たとえば、100 個のクラスター) を生成します。
  4. 第2ラウンドの広範なMDシミュレーションの実施
    1. これら100の初期構造から始めて、すべての原子にランダムな初期速度を課した後、60nsのMDシミュレーションを行います。mdp ファイルの速度生成をオンにすることによって、つまり md.mdp ファイルを gen_vel = no から gen_vel = yes に変更することによって、ランダムな初期速度を追加します。
    2. 手順 1.3.1 で説明したように、各シミュレーションの最初の 10 ns を削除し、100 ~ 50 ns の軌道から 2,500,000 個のスナップショットを均等に収集して、MSM ×構築します。
      注: 後のマクロステート構築では、特に低い母集団(X-Θ平面の底部で〜0.2%)を持つ少数のオフパス状態が見つかったことに注意してください。これらのオフパス状態は、マクロ状態の合計数が 3 ~ 6 に設定されている場合、1 つのマクロ状態として分類されます (図 2B)。このような低母集団のマクロステートは、最終的に除去された3つの軌道のみを含むので、このプロトコルに示された結果は、97×50nsの軌道から実際に得られ、合計2,425,000フレームまたはスナップショットを有する。
  5. 第 2 ラウンド MD 軌道のクラスタリング
    1. 前回と同様に、第 2 ラウンドの軌道に対して tICA を実行します。MSMビルダーに次のように入力します。
      msmb tICA -i ../tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --γ 0.05 -t tica_results.h5
    2. 暗黙のタイムスケールを計算して、相関遅延時間Δtとマイクロステート数のパラメータを検証します( 図1C参照)。
      figure-protocol-6336
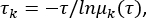
      ここで、τは遷移確率行列(TPM)の構築に使用されるラグタイムを表します。μk(τ) は、τ のラグタイム下での TPM の k 番目の固有値を表します。この Python には 、補足ファイル 1 の Python スクリプト BuildMSMsAsVaryLagTime.py -d を使用します。/ -f ../trajlist_num -i 50 -m 1000 -t 10 -n 20 -s 500.
    3. ラグタイムτとマイクロステートの数を変えるには、上記で使用したパラメータを変更します。
      python BuildMSMsAsVaryLagTime.py -d ../ -f ../trajlist_num -i 50 -m 1000 -t 5 10 20 30 40 -n 20 -s 20 200 400 500 800 2000
      注: 暗黙のタイムスケール曲線がタイムスケール分離で横ばいになり始めると、システムはマルコビアンと見なされます。次に、相関遅延時間として Dt を選択し、MSM を構築するために暗黙のタイムスケールが横ばいになり始めるラグタイムを τ を選択します。
    4. したがって、比較的大きい(ただし大きすぎない)状態数、N = 500、および比較的短い相関遅延時間Δt = 10nsを選択します。MSMを構築するためのラグタイムはτ = 10nsであることが判明しました。
    5. 次のコマンドを使用して、コンフォメーションを 500 個のクラスターに分類します ( 図 1D を参照)。
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 500
  6. MSMの構造
    1. 500 個のマイクロステートを 3 ~ 6 個のマクロステートにまとめて、MSMbuilder の PCCA+ アルゴリズム50 に最も適したマクロステートの数を、補足ファイル 1 の python msm_lumping_usingPCCAplus.pyの python スクリプトを使用して見つけます。少数のマクロステートを構築することによって、すなわち、下記17、51のように何百ものミクロステートを速度論的に集中させることによって、生体分子の最も重要な立体構造変化のためのモデルの縮小された動力学的ネットワークを同定する。
    2. ステップ1.1.3および1.1.4で説明したように、各マクロ状態について、高次元立体配座をX(DNA長軸に沿ったタンパク質移動)およびDNAに沿ったタンパク質の回転角度にマッピングする(例えば、集団が1%<低すぎる状態がない; 図2Cを参照)。次に、システムを最もよく表す3つのマクロ状態を見つけます(図1E)。DNAに沿ったタンパク質の動きとDNA周りのタンパク質回転角度のスナップショットについては、 図2D を参照してください。
      注:10 μsの自発的なタンパク質の順方向ステッピング経路を生成する以前の研究では、サンプリングを適度に拡張するために、5 x 4 μsの平衡MDシミュレーションをさらに実施しました。元の順方向経路(図2A左参照)と、以前に実施した順方向経路上のさらに4μsサンプリング軌道(図2A右参照)のマッピングを示しました8。この作業で使用した元の100 × 50 nsのマッピング(図2B左参照)8と、この作業で使用した97 × 50 nsの軌道を示しています(図2B右参照)。
  7. 平均初回通過時間(MFPT)の計算
    1. MC の時間ステップとしてラグタイムを 10 ns に設定して、500 マイクロステート MSM の TPM に基づいて 5 つの 10 ミリ秒のモンテカルロ (MC) 軌道を実行します。補足ファイル 1 python python mfpt_msm3.py の python スクリプトを使用して、マクロ状態の各ペア間の MFPT52 を計算します (図 3)。
    2. 補足ファイル 2 の bash ファイルを使用して MFPT の平均誤差と標準誤差を計算し、次のように入力します。
      sh mfpt_analysis.bash

2. 長時間のダイナミクスをサンプリングするための粗粒度(CG)シミュレーションの実施

  1. CafeMol 3.0ソフトウェア30を用いてCGシミュレーションを行う。入力構成ファイルで指定されている CG シミュレーション設定 (入力構造、シミュレーション・パラメーター、出力ファイルなどを含む) を拡張子 .inp で確認してください。端末で次のコマンドを入力して、CG シミュレーションを実行します。
    カフェモール XXX.inp
  2. 入力ファイルで以下のブロックを指定し、各ブロックはラベル < and ending with >>>>で始まります。
    1. ファイル名ブロック (必須) を設定して、作業ディレクトリと入出力ファイルストアパスを指定します。これらのシミュレーションのファイル名ブロックに次のように入力します。
      ファイル名の<<<<
      パス = XXXXX (作業パス)
      ファイル名 = wrky (出力ファイル名)
      出力 psf pdb ムービー dcd rst
      path_pdb = XXXXX (入力ネイティブ構造パス)
      path_ini = XXXXX (入力初期構造パス)
      path_natinfo = XXXXX (ネイティブ情報ファイルのパス)
      path_para = XXXXX (パラメーター・ファイル・パス)
      >>>>
      注:Go-model53 はCGモデリングに利用されるため、すなわち、タンパク質は天然の立体構造に偏るため、モデル化された構造を天然の立体構造として設定する必要がある。ここで、入力結晶構造は、天然の立体構造として設定した。
    2. ジョブ制御ブロック(必須)を設定して、シミュレーションの実行モードを定義します。次のコマンドを入力します。
      <<<< job_cntl
      i_run_mode = 2 (= 2 定温シミュレーション)
      i_simulate_type = 1 (=1 ランジュバンダイナミクス)
      i_initial_state = 2 (=2 は初期構成がネイティブ構成であることを意味します)
      >>>>
      定温ランジュバンダイナミクスシミュレーションを選択します。
    3. 単位ブロックと状態ブロック (必須) を設定して、入力構造の情報を定義します。次のコマンドを入力します。
      <<<< unit_and_state
      i_seq_read_style = 1 (=1 は PDB ファイルからのシーケンスの読み取りを意味します)
      i_go_native_read_style = 1 (=1 はネイティブ構造が PDB ファイルからのものであることを意味します)
      1 タンパク質タンパク質.pdb(単位と状態molecular_type native_structure)
      2-3 DNA.pdb (ユニット&ステートmolecular_type native_structure)
      >>>>
      注: 初期入力構造ファイル (タンパク質.pdbおよび DNA.pdb はこちら) が必要です。構造体は pdb 形式で記述されます。ここでは 2 つの pdb ファイルが必要です: 1 つは WRKY の重原子座標を含むタンパク質構造ファイル(ユニット 1)、もう 1 つは 200 bp の二本鎖 (ds) DNA (ユニット 2-3) の座標です。タンパク質は、最初はDNAから15オングストローグメートル離れた位置に配置されます。
    4. energy_functionブロックに定義されているエネルギー関数ブロック(必須)を設定します。次のコマンドを入力します。
      <<<< energy_function
      ローカル(1) L_GO
      ローカル(2-3) L_DNA2
      NLOCAL(1/1) GO EXV ELE
      NLOCAL(2-3/2-3) ELE DNA
      NLOCAL(1/2-3) EXV ELE
      i_use_atom_protein = 0
      i_use_atom_dna = 0
      i_para_from_ninfo = 1
      i_triple_angle_term = 2
      >>>>
      注:CGシミュレーションでは、タンパク質はGoモデル53によって粗粒化され、CG 粒子で表される各アミノ酸はそのCα位置に配置される。タンパク質の立体構造は、Goポテンシャルの下で天然の構造、またはここでは結晶構造に向かって偏ります(図4A 左)。DNAは3SPN.2モデル54によって記述され、各ヌクレオチドは、それぞれ糖、リン酸、および窒素塩基に対応する3CG粒子S、P、Nで表される(図4A 右)。静電相互作用とvdW相互作用は、異なるチェーン間で考慮されます。CGシミュレーションにおけるタンパク質とDNA間の静電相互作用は、デバイ・ヒュッケル電位55によって近似される。vdWの反発エネルギーは囲碁モデルと同じ形をとります。
    5. md_informationブロック(必須)を設定してシミュレーション情報を定義します。次のコマンドを入力します。
      <<<< md_information
      n_step_sim = 1
      n_tstep(1) = 500000000
      tstep_size = 0.1
      n_step_save = 1000
      n_step_neighbor = 100
      i_com_zeroing = 0
      i_no_trans_rot = 0
      テンプ = 300.0
      n_seed = -1
      >>>>
      n_tstepはシミュレーションステップです。各MDステップの時間長としてtstep_sizeを設定し、各CGカフェモールの時間ステップは約200 fs30なので、ここでの各MDステップは原則として200×0.1 fsです。100 MD ステップごとに近隣リストを更新します (n_step_neighbor = 100)。シミュレーション温度を300Kに設定し、速度型Verletアルゴリズムを採用して温度を制御し、ベレンセンサーモスタット56でタンパク質構造を更新します。
      注: n_step_simは、囲碁モデルベースのポテンシャルの流域番号、またはエネルギー曲線のローカル最小数です。複数の流域ポテンシャルは、タンパク質立体構造が異なる立体構造に偏ることを可能にするので、タンパク質立体構造はある局所最小値から別の極小値に変化することができる。ここでは、単一の流域囲碁モデルのみが使用され、シミュレーションにおけるタンパク質の偏った立体構造(結晶構造)は1つだけを意味する。一方、CGの文脈でモデル化されたタンパク質-DNA水素結合相互作用などがないため、分子運動は原子シミュレーションよりもさらに高速、すなわち>10倍サンプリングすることができます。
    6. 静電相互作用が異なるチェーン間で考慮されるように静電ブロック(静電相互作用が使用されている場合にのみ必要)を設定するので、このブロックを使用して、次のように入力して静電相互作用のパラメータを定義します。
      静電<<<<
      cutoff_ele = 10.0
      ionic_strength = 0.15
      >>>>
      静電相互作用における Debye 長を 10 Å に設定し、解条件に対応します。生理学的条件と同様に、イオン強度を0.15 Mに設定してください。

結果

回転結合摺動またはMSM構造からのWRKYの1 bpステッピング
DNA上のすべてのタンパク質立体構造は、DNAに沿ったタンパク質COMの縦方向運動Xおよび回転角度にマッピングされる( 図3A参照)。これら2度の直線結合は、DNA上のWRKYドメインタンパク質の回転結合ステッピングを示す。立体構造は、MSM の 3 つのマクロ状態 (S1、S2、および S3) にさらにクラスター化でき...

ディスカッション

本研究は、構造ベースの計算シミュレーションとサンプリングを行い、DNAに沿って移動する転写因子またはTFタンパク質を、ステッピングの原子詳細だけでなく、DNA標的探索におけるTFの促進拡散に不可欠なプロセス拡散においても明らかにする方法に取り組む。そのために、均質なポリA DNAに沿って1-bpの小さなTFドメインタンパク質WRKYステッピングのマルコフ状態モデルまたはMSMが最初に構...

開示事項

著者には利益相反はありません。

謝辞

この作業は NSFC Grant #11775016 と #11635002 によってサポートされています。JYは、NSF DMS 1763272とサイモンズ財団助成金#594598およびUCIからのスタートアップ基金を通じて、UCIのCMCFによって支援されています。LTDは、上海#20ZR1425400#21JC1403100の自然科学財団の支援を受けています。我々はまた、北京計算科学研究センター(CSRC)からの計算支援を認識する。

資料

NameCompanyCatalog NumberComments
CafeMolKyoto Universitycoarse-grained (CG) simulations
GROMACSUniversity of Groningen Royal Institute of Technology Uppsala Universitymolecular dynamics simulations software
MatlabMathWorksNumerical calculation software
MSMbuilderStanford Universitybuild MSM
VMDUNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGNmolecular visualization program

参考文献

  1. Latchman, D. S. Transcription factors: an overview. The International Journal of Biochemistry & Cell Biology. 29 (12), 1305-1312 (1997).
  2. Berg, O. G., von Hippel, P. H. Selection of DNA binding sites by regulatory proteins. Statistical-mechanical theory and application to operators and promoters. Journal of Molecular Biology. 193 (4), 723-750 (1987).
  3. von Hippel, P. H., Berg, O. G. Facilitated target location in biological systems. The Journal of Biological Chemistry. 264 (2), 675-678 (1989).
  4. Halford, S. E., Marko, J. F. How do site-specific DNA-binding proteins find their targets. Nucleic Acids Research. 32 (10), 3040-3052 (2004).
  5. Slusky, M., Mirny, L. A. Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential. Biophysical Journal. 87 (6), 4021-4035 (2004).
  6. Bauer, M., Metzler, R. Generalized facilitated diffusion model for DNA-binding proteins with search and recognition states. Biophysical Journal. 102 (10), 2321-2330 (2012).
  7. Shvets, A. A., Kochugaeva, M. P., Kolomeisky, A. B. Mechanisms of Protein Search for Targets on DNA: Theoretical Insights. Molecules. 23 (9), 2106 (2018).
  8. Dai, L., Xu, Y., Du, Z., Su, X. D., Yu, J. Revealing atomic-scale molecular diffusion of a plant-transcription factor WRKY domain protein along DNA. Proceedings of the National Academy of Sciences of the United States of America. 118 (23), 2102621118 (2021).
  9. Chodera, J. D., Singhal, N., Pande, V. S., Dill, K. A., Swope, W. C. Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. The Journal of Chemical Physics. 126 (15), 155101 (2007).
  10. Pan, A. C., Roux, B. Building Markov state models along pathways to determine free energies and rates of transitions. The Journal of Chemical Physics. 129 (6), 064107 (2008).
  11. Bowman, G. R., Huang, X., Pande, V. S. Using generalized ensemble simulations and Markov state models to identify conformational states. Methods. 49 (2), 197-201 (2009).
  12. Prinz, J. H., et al. Markov models of molecular kinetics: Generation and validation. The Journal of chemical physics. 134 (17), 174105 (2011).
  13. Chodera, J. D., Noé, F. Markov state models of biomolecular conformational dynamics. Current Opinion in Structural Biology. 25, 135-144 (2014).
  14. Malmstrom, R. D., Lee, C. T., Van Wart, A. T., Amaro, R. E. On the Application of Molecular-Dynamics Based Markov State Models to Functional Proteins. Journal of Chemical Theory and Computation. 10 (7), 2648-2657 (2014).
  15. Husic, B. E., Pande, V. S. Markov State Models: From an Art to a Science. Journal of the American Chemical Society. 140 (7), 2386-2396 (2018).
  16. Sittel, F., Stock, G. Perspective: Identification of collective variables and metastable states of protein dynamics. The Journal of chemical physics. 149 (15), 150901 (2018).
  17. Wang, W., Cao, S., Zhu, L., Huang, X. Constructing Markov State Models to elucidate the functional conformational changes of complex biomolecules. WIREs Computational Molecular Science. 8, 1343 (2018).
  18. Peng, S., et al. Target search and recognition mechanisms of glycosylase AlkD revealed by scanning FRET-FCS and Markov state models. Proceedings of the National Academy of Sciences of the United States of America. 117 (36), 21889-21895 (2020).
  19. Tian, J., Wang, L., Da, L. T. Atomic resolution of short-range sliding dynamics of thymine DNA glycosylase along DNA minor-groove for lesion recognition. Nucleic Acids Research. 49 (3), 1278-1293 (2021).
  20. Chu, J. -. W., Izveko, S., Voth, G. The multiscale challenge for biomolecular systems: coarse-grained modeling. Molecular Simulation. 32 (3-4), 211-218 (2006).
  21. Marrink, S. J., Risselada, H. J., Yefimov, S., Tieleman, D. P., De Vries, A. H. The MARTINI force field: coarse grained model for biomolecular simulations. The Journal of Physical Chemistry B. 111 (27), 7812-7824 (2007).
  22. Givaty, O., Levy, Y. Protein sliding along DNA: dynamics and structural characterization. Journal of Molecular Biology. 385 (4), 1087-1097 (2009).
  23. Khazanov, N., Levy, Y. Sliding of p53 along DNA can be modulated by its oligomeric state and by cross-talks between its constituent domains. Journal of Molecular Biology. 408 (2), 335-355 (2011).
  24. Riniker, S., Allison, J. R., van Gunsteren, W. F. On developing coarse-grained models for biomolecular simulation: a review. Physical Chemistry Chemical Physics : PCCP. 14 (36), 12423-12430 (2012).
  25. Kmiecik, S., et al. Coarse-Grained Protein Models and Their Applications. Chemical Reviews. 116 (14), 7898-7936 (2006).
  26. Bhattacherjee, A., Krepel, D., Levy, Y. Coarse-grained models for studying protein diffusion along DNA. WIREs Computational Molecular Science. 6, 515-531 (2016).
  27. Wang, J., et al. Machine Learning of Coarse-Grained Molecular Dynamics Force Fields. ACS Central Science. 5 (5), 755-767 (2019).
  28. Joshi, S. Y., Deshmukh, S. A. A review of advancements in coarse-grained molecular dynamics simulations. Molecular Simulation. 47 (10-11), 786-803 (2021).
  29. Bigman, L. S., Greenblatt, H. M., Levy, Y. What Are the Molecular Requirements for Protein Sliding along DNA. The Journal of Physical Chemistry B. 125 (12), 3119-3131 (2021).
  30. Kenzaki, H., et al. CafeMol: A Coarse-Grained Biomolecular Simulator for Simulating Proteins at Work. Journal of Chemical Theory and Computation. 7 (6), 1979-1989 (2011).
  31. Berendsen, H. J. C., vander Spoel, D., van Drunen, R. GROMACS: a message-passing parallel molecular dynamics implementation. Computer Physics Communications. 91 (1-3), 43-56 (1995).
  32. vander Spoel, D., et al. GROMACS: fast, flexible, and free. Journal of Computational Chemistry. 26 (16), 1701-1718 (2005).
  33. Abraham, M. J., et al. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 1-2, 19-25 (2015).
  34. Harrigan, M. P., et al. MSMBuilder: Statistical Models for Biomolecular Dynamics. Biophysical journal. 112 (1), 10-15 (2017).
  35. Humphrey, W., Dalke, A., Schulten, K. VMD: visual molecular dynamics. Journal of Molecular Graphics. 14 (1), 33-38 (1996).
  36. Izrailev, S., et al. Steered Molecular Dynamics. Computational Molecular Dynamics: Challenges, Methods, Ideas. 4, 39-65 (1999).
  37. Schlitter, J., Engels, M., Krüger, P. Targeted molecular dynamics: a new approach for searching pathways of conformational transitions. Journal of Molecular Graphics. 12 (2), 84-89 (1994).
  38. Maragliano, L., Fischer, A., Vanden-Eijnden, E., Ciccotti, G. String method in collective variables: minimum free energy paths and isocommittor surfaces. The Journal of Chemical Physics. 125 (2), 24106 (2006).
  39. Weiss, D. R., Levitt, M. Can morphing methods predict intermediate structures. Journal of Molecular Biology. 385 (2), 665-674 (2009).
  40. Xu, Y. P., Xu, H., Wang, B., Su, X. D. Crystal structures of N-terminal WRKY transcription factors and DNA complexes. Protein. 11 (3), 208-213 (2020).
  41. Higham, D. J., Higham, N. J. MATLAB guide. Society for Industrial and Applied Mathematics. , (2016).
  42. Hartigan, J. A., Wong, M. A. Algorithm AS 136: A K-Means Clustering Algorithm. Journal of the Royal Statistical Society. Series C (Applied Statistics). 28 (1), 100-108 (1979).
  43. Gonzalez, T. F. Clustering to minimize the maximum intercluster distance. Theoretical Computer Science. 38, 293-306 (1985).
  44. Zhao, Y., Sheong, F. K., Sun, J., Sander, P., Huang, X. A fast parallel clustering algorithm for molecular simulation trajectories. Journal of Computational Chemistry. 34 (2), 95-104 (2013).
  45. Ivani, I., et al. Parmbsc1: a refined force field for DNA simulations. Nature Methods. 13 (1), 55-58 (2016).
  46. Naritomi, Y., Fuchigami, S. Slow dynamics of a protein backbone in molecular dynamics simulation revealed by time-structure based independent component analysis. The Journal of Chemical Physics. 139 (21), 215102 (2013).
  47. Naritomi, Y., Fuchigami, S. Slow dynamics in protein fluctuations revealed by time-structure based independent component analysis: the case of domain motions. The Journal of Chemical Physics. 134 (6), 065101 (2011).
  48. Pérez-Hernández, G., Paul, F., Giorgino, T., De Fabritiis, G., Noé, F. Identification of slow molecular order parameters for Markov model construction. The Journal of Chemical Physics. 139 (1), 015102 (2013).
  49. McGibbon, R. T., Pande, V. S. Variational cross-validation of slow dynamical modes in molecular kinetics. The Journal of Chemical Physics. 142 (12), 124105 (2015).
  50. Deuflhard, P., Weber, M. Robust Perron cluster analysis in conformation dynamics. Linear Algebra and its Applications. 398, 161-184 (2005).
  51. Silva, D. A., et al. Millisecond dynamics of RNA polymerase II translocation at atomic resolution. Proceedings of the National Academy of Sciences of the United States of America. 111 (21), 7665-7670 (2014).
  52. Swope, W. C., Pitera, J. W., Suits, F. Describing Protein Folding Kinetics by Molecular Dynamics Simulations. 1. Theory. The Journal of Physical Chemistry B. 108 (21), 6571-6581 (2004).
  53. Clementi, C., Nymeyer, H., Onuchic, J. N. Topological and energetic factors: what determines the structural details of the transition state ensemble and "en-route" intermediates for protein folding? An investigation for small globular proteins. Journal of molecular biology. 298 (5), 937-953 (2000).
  54. Hinckley, D. M., Freeman, G. S., Whitmer, J. K., De Pablo, J. J. An experimentally-informed coarse-grained 3-Site-Per-Nucleotide model of DNA: structure, thermodynamics, and dynamics of hybridization. The Journal of chemical physics. 139 (14), 144903 (2013).
  55. Debye, P., Huckel, E. The theory of the electrolyte II-The border law for electrical conductivity. Physikalische Zeitschrift. 24, 305-325 (1923).
  56. Berendsen, H. J., Postma, J. V., van Gunsteren, W. F., DiNola, A., Haak, J. R. Molecular dynamics with coupling to an external bath. The Journal of Chemical Physics. 81, 3684-3690 (1984).
  57. Bowman, G. R. Improved coarse-graining of Markov state models via explicit consideration of statistical uncertainty. The Journal of Chemical Physics. 137 (13), 134111 (2012).
  58. Jain, A., Stock, G. Identifying metastable states of folding proteins. Journal of Chemical Theory and Computation. 8 (10), 3810-3819 (2012).
  59. Röblitz, S., Weber, M. Fuzzy spectral clustering by PCCA+: application to Markov state models and data classification. Advances in Data Analysis and Classification. 7, 147-179 (2013).
  60. Mardt, A., Pasquali, L., Wu, H., Noé, F. VAMPnets for deep learning of molecular kinetics. Nature Communications. 9 (1), 5 (2018).
  61. Wang, W., Liang, T., Sheong, F. K., Fan, X., Huang, X. An efficient Bayesian kinetic lumping algorithm to identify metastable conformational states via Gibbs sampling. The Journal of Chemical Physics. 149 (7), 072337 (2018).
  62. Chen, W., Sidky, H., Ferguson, A. L. Nonlinear discovery of slow molecular modes using state-free reversible VAMPnets. The Journal of Chemical Physics. 150 (21), 214114 (2019).
  63. Gu, H., et al. RPnet: a reverse-projection-based neural network for coarse-graining metastable conformational states for protein dynamics. Physical Chemistry Chemical Physics :PCCP. 24 (3), 1462-1474 (2022).
  64. Lane, T. J., Bowman, G. R., Beauchamp, K., Voelz, V. A., Pande, V. S. Markov state model reveals folding and functional dynamics in ultra-long MD trajectories. Journal of the American Chemical Society. 133 (45), 18413-18419 (2011).
  65. Konovalov, K. A., Unarta, I. C., Cao, S., Goonetilleke, E. C., Huang, X. Markov State Models to Study the Functional Dynamics of Proteins in the Wake of Machine Learning. JACS Au. 1 (9), 1330-1341 (2021).
  66. Cao, S., Montoya-Castillo, A., Wang, W., Markland, T. E., Huang, X. On the advantages of exploiting memory in Markov state models for biomolecular dynamics. The Journal of Chemical Physics. 153 (1), 014105 (2020).
  67. Brandani, G. B., Takada, S. Chromatin remodelers couple inchworm motion with twist-defect formation to slide nucleosomal DNA. PLoS Computational Biology. 14 (11), 1006512 (2018).
  68. Tan, C., Terakawa, T., Takada, S. Dynamic Coupling among Protein Binding, Sliding, and DNA Bending Revealed by Molecular Dynamics. Journal of the American Chemical Society. 138 (27), 8512-8522 (2016).
  69. Terakawa, T., Takada, S. p53 dynamics upon response element recognition explored by molecular simulations. Scientific reports. 5, 17107 (2015).
  70. Brandani, G. B., Niina, T., Tan, C., Takada, S. DNA sliding in nucleosomes via twist defect propagation revealed by molecular simulations. Nucleic Acids Research. 46 (6), 2788-2801 (2018).
  71. Knotts, T. A., Rathore, N., Schwartz, D. C., de Pablo, J. J. A coarse grain model for DNA. The Journal of Chemical Physics. 126 (8), 084901 (2007).
  72. Freeman, G. S., Hinckley, D. M., Lequieu, J. P., Whitmer, J. K., de Pablo, J. J. Coarse-grained modeling of DNA curvature. The Journal of Chemical Physics. 141 (16), 165103 (2014).

転載および許可

このJoVE論文のテキスト又は図を再利用するための許可を申請します

許可を申請

さらに記事を探す

181

This article has been published

Video Coming Soon

JoVE Logo

個人情報保護方針

利用規約

一般データ保護規則

お問い合わせ

図書館への推薦

JoVE ニュースレター

研究

教育

著者

図書館員

JoVEについて

Copyright © 2023 MyJoVE Corporation. All rights reserved