16.10 : Solubility Equilibria

Solubility equilibria are established when the dissolution and precipitation of a solute species occur at equal rates. These equilibria underlie many natural and technological processes, ranging from tooth decay to water purification. An understanding of the factors affecting compound solubility is, therefore, essential to the effective management of these processes. This section applies previously introduced equilibrium concepts and tools to systems involving dissolution and precipitation.

The Solubility Product

Recall that the solubility of a substance can vary from essentially zero (insoluble or sparingly soluble) to infinity (miscible). A solute with finite solubility can yield a saturated solution when it is added to a solvent in an amount exceeding its solubility, resulting in a heterogeneous mixture of the saturated solution and the excess, undissolved solute. For example, a saturated solution of silver chloride is one in which the equilibrium shown below has been established.

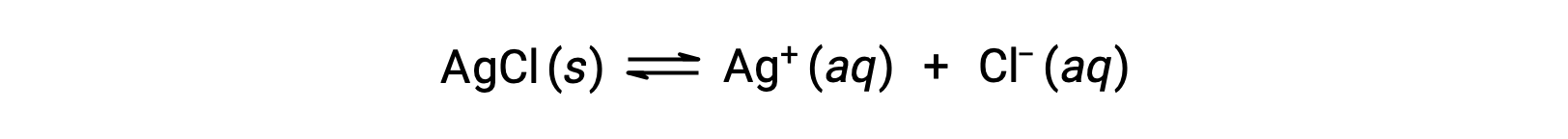
In this solution, an excess of solid AgCl dissolves and dissociates to produce aqueous Ag⁺ and Cl^– ions at the same rate that these aqueous ions combine and precipitate to form solid AgCl. Because silver chloride is a sparingly soluble salt, the equilibrium concentration of its dissolved ions in the solution is relatively low.

The equilibrium constant for solubility equilibria such as this one is called the solubility product constant, K_sp, in this case

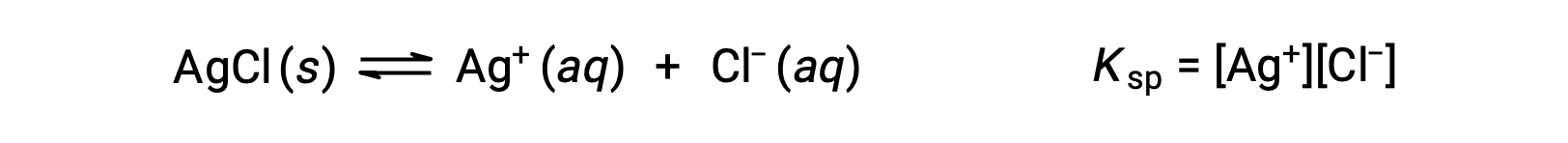
Recall that only gases and solutes are represented in equilibrium constant expressions, so the K_sp does not include a term for the undissolved AgCl.

K_sp and Solubility

The K_sp of a slightly soluble ionic compound may be simply related to its measured solubility provided the dissolution process involves only dissociation and solvation, for example:

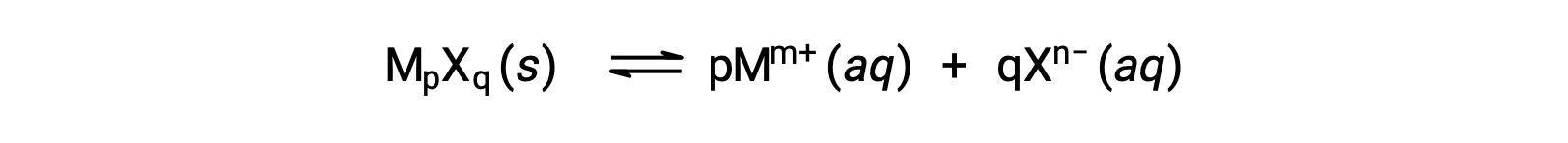
For cases such as these, one may derive K_sp values from provided solubilities, or vice-versa. Calculations of this sort are most conveniently performed using a compound’s molar solubility, measured as moles of dissolved solute per liter of saturated solution.

Predicting Precipitation

The equation that describes the equilibrium between solid calcium carbonate and its solvated ions is:

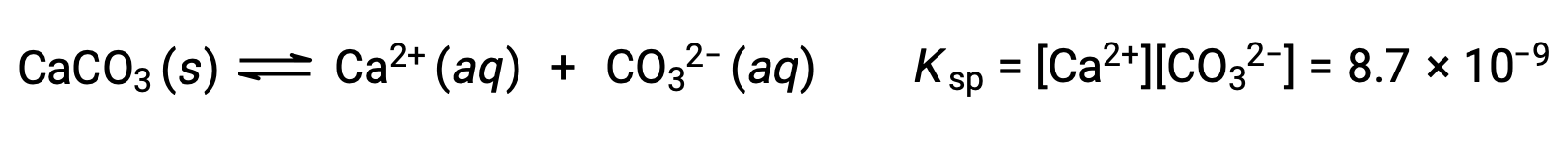
It is important to realize that this equilibrium is established in any aqueous solution containing Ca²⁺ and CO₃^2– ions, not just in a solution formed by saturating water with calcium carbonate. Consider, for example, mixing aqueous solutions of the soluble compounds sodium carbonate and calcium nitrate. If the concentrations of calcium and carbonate ions in the mixture do not yield a reaction quotient, Q, that exceeds the solubility product, K_sp, then no precipitation will occur. If the ion concentrations yield a reaction quotient greater than the solubility product, then precipitation will occur, lowering those concentrations until equilibrium is established (Q = K_sp). The comparison of Q to K_sp to predict precipitation is an example of the general approach to predicting the direction of a reaction first introduced in the lessons on equilibrium. For the specific case of solubility equilibria:

Q < K_sp: the reaction proceeds in the forward direction (the solution is not saturated; no precipitation observed)

Q > K_sp: the reaction proceeds in the reverse direction (the solution is supersaturated; precipitation will occur)

This text is adapted from Openstax, Chemistry 2e, Section 15.1: Precipitation and Dissolution.