Messung von Chladni-Modus-Formen mit einer optischen Hebelmethode

Zusammenfassung

Es wird eine einfache Methode zur Messung der Chladni-Modusform auf einer elastischen Platte nach dem Prinzip eines optischen Hebels vorgeschlagen.

Zusammenfassung

Die quantitative Bestimmung des Chladni-Musters einer elastischen Platte ist sowohl in der Physik als auch in technischen Anwendungen von großem Interesse. In diesem Papier wird eine Methode zur Messung von Modusformen einer Vibrationsplatte auf der Grundlage eines optischen Hebelverfahrens vorgeschlagen. Bei der Messung wurden drei kreisförmige Acrylplatten unter verschiedenen mittelharmonischen Anregungen eingesetzt. Anders als bei einer herkömmlichen Methode werden bei diesem neuartigen Ansatz nur ein gewöhnlicher Laserstift und ein Lichtschirm aus gemahlenem Glas verwendet. Der Ansatz ist wie folgt: Der Laserstift projiziert einen Strahl senkrecht auf die vibrierende Platte, und dann wird der Strahl auf den Lichtschirm in der Ferne reflektiert, auf dem ein Liniensegment aus dem reflektierten Punkt gebildet wird. Aufgrund des Prinzips der Sehpersistenz konnte der Lichtfleck als helle gerade Linie gelesen werden. Die Beziehung zwischen der Neigung der Modusform, der Länge des Lichtflecks und dem Abstand der Vibrationsplatte und des Lichtschirms kann mit algebraischen Operationen erreicht werden. Dann kann die Modusform durch Die Integration der Neigungsverteilung mit geeigneten Randbedingungen bestimmt werden. Auch die Vollfeldmodusformen der Chladni-Platte könnten so einfach weiter bestimmt werden.

Einleitung

Chladni-Modus-Formen sind sowohl in wissenschaftlichen als auch in technischen Anwendungen von großem Interesse. Chladni-Muster sind Reaktionen physischer Wellen, und man kann das Wellenmuster mit verschiedenen Methoden veranschaulichen. Es ist eine bekannte Methode, um die verschiedenen Schwingungsarten auf einer elastischen Platte zu zeigen, indem die Knotenlinien umrissen werden. Kleine Partikel werden immer verwendet, um die Chladni-Muster zu zeigen, da sie an den Knoten anhalten können, wo die relative vibrierende Amplitude der Platte Null ist, und die Positionen der Knoten variieren mit dem Resonanzmodus, um verschiedene Chladni-Muster zu bilden.

Viele Forscher haben auf verschiedene Chladni-Muster geachtet, aber sie zeigen nur die Knotenlinien der Modusformen, die Modusformen (d. h. Schwingungsamplitude) zwischen den Knotenlinien werden nicht dargestellt. Waller untersuchte die freien Schwingungen eines Kreises¹, eines^{Quadrats 2}, eines isosceles rechtwinkligen Dreiecke³, eines rechteckigen⁴, elliptischen⁵ Platten, und verschiedene Chladni-Muster sind darin dargestellt. Tuan et al. rekonstruierten verschiedene Chladni-Muster durch experimentelle und theoretische Ansätze, und die inhomogene Helmholtz-Gleichung wird während der theoretischen Modellierung^{angenommen 6,7}. Es ist eine beliebte Methode der Verwendung von Laser Doppler Vibrometer (LDV) oder Electronic Speckle Pattern Interferometry (ESPI) quantitativ messen die Modusformen der Chladni Muster^8,9,10. Obwohl LDV femtometer Amplitude Auflösung und sehr hohe Frequenzbereiche ermöglicht, ist der Preis von LDV leider auch ein wenig teuer für Klassenzimmer Demonstration und / oder College-Physik-Unterricht. Unter dieser Überlegung schlug das vorliegende Papier einen einfachen Ansatz vor, um die Modusformen eines Chladni-Musters mit geringen Kosten quantitativ zu bestimmen, da hier nur ein zusätzlicher Laserstift und ein Lichtschirm benötigt werden.

Die vorliegende Messmethode ist in Abbildung 1¹¹dargestellt. Die Vibrationsplatte hat drei verschiedene Positionen: die Ruheposition, Position 1 und Position 2. Position 1 und 2 stellen die beiden maximalen vibrationsbelebenden Stellen der Platte dar. Ein Laserstift projiziert einen geraden Strahl auf die Oberfläche der Platte, und wenn sich die Platte an der Ruheposition befindet, wird der Laserstrahl direkt auf den Lichtschirm reflektiert. Während sich die Platte an Position 1 und 2 befindet, wird der Laserstrahl auf Punkt A bzw. B auf dem Lichtbildschirm reflektiert. Aufgrund der Wirkung der Persistenz des Sehens, wird es eine helle gerade Linie auf dem Lichtbildschirm geben. Die Länge des hellen Lichts L hängt mit dem Abstand D zwischen dem Lichtbildschirm und der Position des Laserpunkts zusammen. Verschiedene Punkte auf der Platte haben unterschiedliche Steigungen, die durch die Beziehung zwischen L und Dbestimmt werden könnten. Nachdem die Neigung der Modusform an verschiedenen Stellen auf der Platte erhalten wurde, wird das Problem zu einem bestimmten Integral. Mit Hilfe der Grenzschwingungsamplitude der Platte und der diskreten Neigungsdaten kann die Modusform der Vibrationsplatte leicht ermittelt werden. Der gesamte Versuchsaufbau ist in Abbildung 2¹¹dargestellt.

In diesem Artikel werden die versuchsweise Einrichtung und das Verfahren für die Methode des optischen Hebels zur Messung der Formen im Chladni-Modus beschrieben. Einige typische experimentelle Ergebnisse werden ebenfalls veranschaulicht.

Protokoll

1. Versuchsaufbau und Verfahren

ANMERKUNG: Richten Sie das experimentelle System wie in Abbildung 2dargestellt ein.

1. Vorbereitung des Schwingungssystems
   1. Bereiten Sie drei 1,0 mm dicke gespiegelte kreisförmige Acrylplatten mit einem Durchmesser von 150 mm, 200 mm bzw. 250 mm vor. Bohren Sie ein Loch von 3 mm Durchmesser in der Mitte jeder Platte. Markieren Sie mehrere schwarze Punkte alle 5 mm entlang eines beliebigen Radius.
   2. Befestigen Sie jede Platte mit einer Schraube im Mittelpunkt an der Betätigungsstange des Vibrators. Fahren Sie den Vibrator mit einer Sinuswelle mit einem Wellenformgenerator, und die Standardeinstellungen reichen für das Resonanzexperiment aus.
      HINWEIS: Die Anregungsrichtung des Vibrators ist horizontal, um den Bildschirm anschließend zu bewegen.
   3. Erfassung der Resonanzfrequenz
      1. Platzieren Sie den Laserstift, um den Laserstrahl senkrecht auf die vibrierende Platte zu projizieren, so dass der Strahl in der Ferne auf den Lichtschirm reflektiert wird. Die Abstände zwischen dem Laserstift und der Platte und dem Lichtschirm betragen 120 mm bzw. 500 mm.
         HINWEIS: Je weiter der Abstand zwischen dem Lichtschirm und der vibrationsschwingenden Platte liegt, desto offensichtlicher erscheint das Phänomen. Es wird auch darauf hingewiesen, dass die vorliegende Methode verwendet werden kann, um entweder achsensymmetrische oder nicht-axisymmetrische Modus-Shapes zu messen. Aufgrund der Einfachheit und Bequemlichkeit zeigt das vorliegende Manuskript nur die Anwendung bei der Bestimmung der achsensymmetrischen Modusformen von drei kreisförmigen Platten. Dann müssen wir nur die Schwingungsamplitude entlang jeder radialen Richtung messen, um die zweidimensionale Modusform der Platte zu rekonstruieren.
      2. Bewegen Sie den Laserstift entlang der Richtung senkrecht zu seiner Längenrichtung, um den Einfallspunkt über einen Durchmesser scannen zu lassen, während der Signalgenerator seine Frequenz kontinuierlich ändert. Tun Sie es schnell, bis die Spotlänge beim Scannen in einem bestimmten Frequenzbereich signifikant entlang des Durchmessers gestreckt wird und einige Flecken mit fast keiner Ausdehnung erscheinen. Für die Platte mit einem Durchmesser von 150 mm, 200 mm und 250 mm betragen die gefegten Frequenzbereiche 200-400 Hz, 100-300 Hz bzw. 50-250 Hz.
      3. Scannen Sie diesen bestimmten Frequenzbereich langsam und wählen Sie die Frequenz aus, mit der sich der Spot am offensichtlichsten ausdehnt. Es wird festgestellt, dass für die Platte mit einem Durchmesser von 150 mm, 200 mm und 250 mm die Resonanzfrequenzen 346 Hz, 214 Hz bzw. 150 Hz betragen.
2. Vorbereitung des Lichtweg- und Messsystems
   1. Platzieren Sie den Lichtschirm parallel zur Vibrationsplatte. Markieren Sie den Abstand mit einem Meterlineal, und verwenden Sie 500 mm als Startabstand.
   2. Platzieren Sie den Laserstift, um den Strahl senkrecht auf die Platte zu projizieren, so dass der Strahl in der Ferne auf den Lichtschirm reflektiert wird. Stellen Sie sicher, dass die zuvor gemachte Markierung gescannt werden kann, während sich der Laserstift bewegt.
      HINWEIS: Das Laserstrahllicht muss senkrecht auf die Platte projiziert werden.
3. Experimentelle Messung
   1. Schalten Sie den Signalgenerator ein und stellen Sie die Anregungsfrequenz so ein wie die Resonanzfrequenz, die in Schritt 1.1.3.3 erreicht wurde. Die Signalintensität sollte so klein wie möglich sein, sobald der Lichtfleck auf dem Lichtbildschirm groß genug ist, um aufgezeichnet zu werden.
   2. Passen Sie den Laserstift so an, dass der Einfallpunkt mit dem ersten Marker übereinstimmt, der der nächste Marker zum Fixpunkt der Platte ist.
   3. Bewegen Sie den Bildschirm aus einem Abstand Von D von 500 mm auf 1000 mm und messen Sie die Spotlänge L auf dem Bildschirm alle 50 mm. Zeichnen Sie Daten in tabellarischer Form auf.
   4. Passen Sie den Laserstift an, um den Einfallpunkt neben dem nächsten Marker zu machen, und wiederholen Sie Schritt 1.3.3, bis alle Marker gemessen wurden.
      HINWEIS: Da Acrylplatten unter Anregung leicht plastisch verformt werden können, kann der experimentelle Messprozess einer Platte nicht lange angehalten werden.
   5. Ersetzen Sie die frühere Platte durch die nächste und wiederholen Sie die Schritte 1.3.1 bis 1.3.4.

2. Datenverarbeitung

1. Bestimmen Sie den Winkel zwischen dem Einfallen und dem reflektierten Licht mit der Beziehung:
   
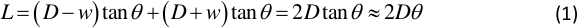
   wobei D der Abstand zwischen der Restposition der Vibrationsplatte und dem Lichtschirm ist, w die Amplitude der Platte vibriert und L die Länge des Lichtflecks auf dem Lichtbildschirm ist. Mehrere Paare von D und L werden in Schritt 1.3.3 erhalten.
2. Bestimmen Sie die Neigung 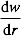der Modusform durch:
   
   HINWEIS: Die erhaltene Steigung ist bei Eqs immer positiv. (1) und (2).
3. Verwenden Sie ein Minuszeichen zwischen zwei Nullpunkten, um die wahre Neigungsverteilung zu erhalten.
   HINWEIS: Es spielt keine Rolle, ob die Revision vom ersten oder zweiten Nullpunkt beginnt.
4. Integrieren Sie die Neigungsverteilung jeder Platte und bestimmen Sie die integrale Konstante durch die Knoten, um die Modusform zu erhalten mit:
   
   HINWEIS: Knoten entsprechen der größten Neigung des Modus-Shapes. ist eine Konstante, die durch die Position der Knotenlinien des Chladni-Musters bestimmt wird, die in Abbildung 2dargestellt sind.
5. Berechnen Sie die Unsicherheit der Steigung¹² mit:
   
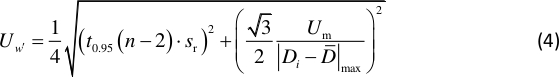
   ANMERKUNG: t_0,95(n – 2) ist der t Verteilungsfaktor mit 95% Vertrauen und Freiheitsgraden n-2, und es ist etwa 2 hier. S_r ist der Standardfehler der linearen Regression mit D und L, U_m bezeichnet die Unsicherheit des gemessenen Abstands Di_iund ist hier 0,5 mm. Die durchschnittliche gemessene Entfernung wird durch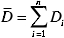 definiert, und n bezeichnet die Gesamtzahl der gemessenen D_i.

Ergebnisse

Die Anregungsfrequenz, die das axisymmetrische Chladni-Muster anregen kann, wird durch den Frequenzfeisionstest bestimmt. Es werden drei kreisförmige Acrylplatten mit Durchmessern von 150 mm, 200 mm und 250 mm getestet, und die Ergebnisse zeigen, dass die axisymmetrischen Resonanzfrequenzen erster Ordnung 346 Hz, 214 Hz und 150 Hz für die drei Platten sind. Es wird der Schluss gezogen, dass die Platte mit größerem Durchmesser flexibler ist und die entsprechende Resonanzfrequenz kleiner wird. Die Chladni-Muster der Ac...

Diskussion

Die methode des optischen Hebels wird in diesem Papier verwendet, um die Modusform einer Platte zu bestimmen, da das Chladni-Muster nur die Knotenlinien einer vibrierenden Platte zeigen kann. Um die Modusform der Platte zu bestimmen, sollte die Beziehung zwischen Neigung und Abstand des Lichtschirms und der Spotlänge im Voraus ermittelt werden. Dann konnte durch eine bestimmte Integrationsberechnung die Modusform des Chladni-Musters quantitativ bestimmt werden.

Im Allgemeinen umfasst der gesa...

Materialien

Name	Company	Catalog Number	Comments
Acrylic plates	Dongguan Jinzhu Lens Products Factory		Three 1.0-mm-thickness mirrored circular acrylic plates with diameter of 150 mm, 200 mm and 250 mm respectively. They are easily deformed.
Laser pen	Deli Group	2802	Red laser is more friendly to the viewer. The finer the laser beam, the better.
Light screen	Northern Tempered Glass Custom Taobao Store		Several layers of frosted stickers can be placed on the glass to achieve the effect of frosted glass.
Ruler	Deli Group	DL8015	The length is 1m and the division value is 1mm.
Signal generator	Dayang Science Education Taobao Store	TFG6920A	Common ones in university laboratories are available.
Vibrator	Dayang Science Education Taobao Store		The maximum amplitude is 1.5cm.The power is large enough to cause a noticeable phenomenon when the board vibrates. Otherwise, add a power amplifier.