Mesure des formes de mode Chladni avec une méthode de levier optique

Résumé

Une méthode simple de mesure de la forme du mode Chladni sur une plaque élastique par le principe d’un levier optique est proposée.

Résumé

La détermination quantitative du modèle Chladni d’une plaque élastique est d’un grand intérêt pour les applications de sciences physiques et d’ingénierie. Dans cet article, une méthode de mesure des formes de mode d’une plaque vibrante basée sur une méthode de levier optique est proposée. Trois plaques acryliques circulaires ont été employées dans la mesure sous différentes excitations harmoniques de centre. Différent d’une méthode traditionnelle, seuls un stylo laser ordinaire et un écran lumineux en verre moulu sont utilisés dans cette nouvelle approche. L’approche est la suivante : le stylo laser projette un faisceau vers la plaque vibrante perpendiculairement, puis le faisceau est réfléchi à l’écran lumineux au loin, sur lequel se forme un segment de ligne fait de l’endroit réfléchi. En raison du principe de persistance de la vision, la tache lumineuse pourrait être lue comme une ligne droite brillante. La relation entre la pente de la forme du mode, la longueur du point lumineux et la distance de la plaque vibrante et l’écran lumineux peut être obtenue avec les opérations algébriques. Ensuite, la forme du mode peut être déterminée en intégrant la distribution de la pente avec des conditions limites appropriées. Les formes de mode plein champ de la plaque Chladni pourraient également être déterminées d’une manière aussi simple.

Introduction

Les formes de mode Chladni sont d’un grand intérêt pour les applications scientifiques et techniques. Chladni modèles sont des réactions d’ondes physiques, et on peut illustrer le modèle d’onde avec diverses méthodes. Il s’agit d’une méthode bien connue pour montrer les différents modes de vibration sur une plaque élastique en décrivant les lignes nodales. De petites particules sont toujours utilisées pour montrer les motifs chladni, car elles peuvent s’arrêter aux nœuds où l’amplitude vibrante relative de la plaque est nulle, et les positions des nœuds varient selon le mode résonnant pour former divers modèles de Chladni.

Beaucoup de chercheurs ont prêté attention à divers modèles de Chladni, mais ils ne montrent que les lignes nodales des formes de mode, les formes de mode (c.-à-d., amplitude vibratoire) entre les lignes nodales ne sont pas illustrées. Waller a étudié les vibrations libres d’un^{cercle 1}, un^{carré 2}, un isoscèle triangles inclinés à droite³, un rectangulaire⁴, elliptique⁵ plaques, et différents modèles Chladni sont illustrés dans. Tuan et coll. ont reconstruit différents modèles de Chladni à travers des approches expérimentales et théoriques, et l’équation inhomogène de Helmholtz est adoptée au cours de la^{modélisation théorique 6,7}. Il s’agit d’une méthode populaire d’utilisation laser Doppler Vibrometer (LDV) ou Electronic Speckle Pattern Interferometry (ESPI) pour mesurer quantitativement les formes de mode des modèles Chladni^8,9,10. Bien que le LDV permette la résolution d’amplitude de femtometer et les gammes très élevées de fréquence, malheureusement, le prix du LDV est également un peu cher pour la démonstration de salle de classe et/ou l’éducation de physique d’université. Avec cette considération, le présent document proposait une approche simple pour déterminer quantitativement les formes de mode d’un modèle Chladni à faible coût, puisque seulement un stylo laser supplémentaire et un écran lumineux sont nécessaires ici.

La méthode de mesure actuelle est illustrée à la figure 11. La plaque vibrante a trois positions différentes : la position de repos, la position 1 et la position 2. Les positions 1 et 2 représentent les deux endroits vibrants maximum de la plaque. Un stylo laser projette un faisceau droit à la surface de la plaque, et si la plaque se trouve à la position de repos, le faisceau laser sera directement réfléchi à l’écran lumineux. Alors que la plaque se trouve à la position 1 et 2, puis le faisceau laser sera réfléchi au point A et B sur l’écran lumineux, respectivement. En raison de l’effet de la persistance de la vision, il y aura une ligne droite lumineuse sur l’écran lumineux. La longueur de la lumière lumineuse L est liée à la distance D entre l’écran lumineux et l’emplacement du point laser. Différents points sur la plaque ont des pentes différentes, qui pourraient être déterminées par la relation entre L et D. Après avoir obtenu la pente de la forme du mode à différents points de la plaque, le problème se transforme en une intégrale définie. Avec l’aide de l’amplitude de vibration limite de la plaque et les données discrètes de pente, la forme de mode de la plaque vibrante peut être obtenue facilement. Toute la configuration expérimentale est donnée à la figure 2¹¹.

Cet article décrit la configuration expérimentale et la procédure de la méthode du levier optique pour mesurer les formes du mode Chladni. Certains résultats expérimentaux typiques sont également illustrés.

Protocole

1. Configuration expérimentale et procédures

REMARQUE : Configurer le système expérimental tel qu’il est indiqué dans la figure 2.

1. Préparation du système de vibration
   1. Préparer trois plaques acryliques circulaires miroir de 1,0 mm d’épaisseur d’un diamètre de 150 mm, 200 mm et 250 mm respectivement. Percer un trou de 3 mm de diamètre au centre de chaque plaque. Marquer plusieurs points noirs tous les 5 mm le long d’un rayon arbitraire.
   2. Attachez chaque plaque à la barre d’actionnement du vibrateur avec un boulon au milieu. Conduisez le vibrateur avec une onde sinusoïde à l’aide d’un générateur de forme d’onde, et les paramètres par défaut seront suffisants pour l’expérience de résonance.
      REMARQUE : La direction d’excitation du vibrateur est horizontale pour la commodité de déplacer l’écran par la suite.
   3. Acquisition de la fréquence de résonance
      1. Placez le stylo laser pour projeter le faisceau laser à la plaque vibrante perpendiculairement de sorte que le faisceau est réfléchi à l’écran lumineux dans la distance. Les distances entre le stylo laser et la plaque et l’écran lumineux sont respectivement de 120 mm et 500 mm.
         REMARQUE : Plus la distance entre l’écran lumineux et la plaque vibrante est grande, plus le phénomène apparaît évident. Il est également noté que la méthode actuelle peut être utilisée pour mesurer les formes axisymétriques ou non axisymétriques du mode. En raison de la simplicité et de la commodité, le présent manuscrit ne démontre que l’application dans la détermination des formes de mode axisymétrique de trois plaques circulaires. Ensuite, nous avons juste besoin de mesurer l’amplitude de vibration le long de n’importe quelle direction radiale pour reconstruire la forme en mode bidimensionnel de la plaque.
      2. Déplacez le stylo laser le long de la direction perpendiculaire à sa direction de longueur pour faire le balayage point incident sur un diamètre tandis que le générateur de signal changer sa fréquence en permanence. Faites-le rapidement jusqu’à ce que la longueur de la tache soit considérablement étirée le long du diamètre lors de la numérisation dans une certaine plage de fréquences, et certains endroits avec presque aucune expansion apparaissent. Pour la plaque d’un diamètre de 150 mm, 200 mm et 250 mm, les plages de fréquence balayées sont respectivement de 200 à 400 Hz, 100-300 Hz et 50-250 Hz.
      3. Numérisez lentement cette certaine plage de fréquences et choisissez la fréquence à laquelle l’endroit se dilate le plus évidemment. On trouve que pour la plaque d’un diamètre de 150 mm, 200 mm et 250 mm, les fréquences de résonance sont respectivement de 346 Hz, 214 Hz et 150 Hz.
2. Préparation du chemin lumineux et du système de mesure
   1. Placez l’écran lumineux parallèlement à la plaque vibrante. Marquez la distance avec une règle de compteur, et utilisez 500 mm comme distance de départ.
   2. Placez le stylo laser pour projeter le faisceau perpendiculairement sur la plaque de sorte que le faisceau soit réfléchi à l’écran lumineux au loin. Assurez-vous que la marque faite avant peut être numérisée pendant que le stylo laser se déplace.
      REMARQUE : La lumière du faisceau laser doit être projetée perpendiculairement sur la plaque.
3. Mesure expérimentale
   1. Allumez le générateur de signal et réglez la fréquence d’excitation comme étant la même que la fréquence de résonance obtenue à l’étape 1.1.3.3. L’intensité du signal doit être aussi faible que possible une fois que le point lumineux de l’écran lumineux est suffisamment grand pour être enregistré.
   2. Ajustez le stylo laser pour faire coïncider le point d’incident avec le premier marqueur, qui est le marqueur le plus proche du point fixe de la plaque.
   3. Déplacez l’écran d’une distance D de 500 mm à 1000 mm et mesurez la longueur de la tache L sur l’écran tous les 50 mm. Enregistrez les données sous forme tabulaire.
   4. Ajustez le stylo laser pour faire le point d’incident adjacent au marqueur suivant à son tour et répétez l’étape 1.3.3 jusqu’à ce que tous les marqueurs aient été mesurés.
      REMARQUE : Puisque les plaques acryliques sont facilement déformées plastiquement sous excitation, le processus expérimental de mesure d’une plaque ne peut pas être mis en pause pendant une longue période.
   5. Remplacez l’ancienne plaque par la plaque suivante et répétez les étapes 1.3.1 à 1.3.4.

2. Traitement des données

1. Déterminez l’angle θ entre l’incident et la lumière réfléchie avec la relation :
   
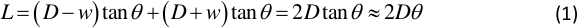
   où D est la distance entre la position de repos de la plaque vibrante et l’écran lumineux, w vibre amplitude de la plaque, et L est la longueur du point lumineux sur l’écran lumineux. Plusieurs paires de D et L sont obtenues à l’étape 1.3.3.
2. Déterminez la pente 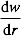de la forme du mode en :
   
   REMARQUE : La pente obtenue est toujours positive avec les QE. (1) et (2).
3. Utilisez un signe moins entre deux points zéro pour obtenir la vraie répartition de la pente.
   REMARQUE : Peu importe que la révision commence à partir du premier ou du deuxième point zéro.
4. Intégrer la répartition de la pente de chaque plaque et déterminer la constante intégrale par les nœuds pour obtenir la forme du mode avec :
   
   REMARQUE : Les nœuds correspondent à la plus grande pente de la forme du mode. est une constante déterminée par l’emplacement des lignes nodales du modèle Chladni indiqués à la figure 2.
5. Calculez l’incertitude de la pente¹² avec :
   
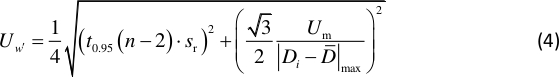
   NOTE: t_0,95(n - 2) est le facteur de distribution t avec 95% de confiance et des degrés de liberté n-2, et il est d’environ 2 ici. S_r est l’erreur standard de la régression linéaire avec D et L, U_{m dénote} l’incertitude de la distance mesurée D_i, et est de 0,5 mm ici. La distance mesurée moyenne est définie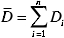 par , et n désigne le nombre total de D i_mesurée.

Résultats

La fréquence d’excitation qui peut exciter le modèle axisymétrique de Chladni est déterminée par le test de balayage de fréquence. Trois plaques acryliques circulaires d’un diamètre de 150 mm, 200 mm et 250 mm sont testées, et les résultats montrent que les fréquences de résonance axisymétrique de premier ordre sont respectivement de 346 Hz, 214 Hz et 150 Hz pour les trois plaques. On conclut qu’avec un diamètre plus grand, la plaque est plus flexible, et la fréquence de résonance correspondante sera...

Discussion

La méthode du levier optique est adoptée dans cet article pour déterminer la forme de mode d’une plaque, puisque le motif Chladni ne peut montrer que les lignes nodales d’une plaque vibrante. Pour déterminer la forme du mode de la plaque, la relation entre la pente et la distance de l’écran lumineux et la longueur du spot doit être obtenue à l’avance. Ensuite, grâce à un calcul d’intégration défini, la forme du mode du modèle Chladni pourrait être déterminée quantitativement.

matériels

Name	Company	Catalog Number	Comments
Acrylic plates	Dongguan Jinzhu Lens Products Factory		Three 1.0-mm-thickness mirrored circular acrylic plates with diameter of 150 mm, 200 mm and 250 mm respectively. They are easily deformed.
Laser pen	Deli Group	2802	Red laser is more friendly to the viewer. The finer the laser beam, the better.
Light screen	Northern Tempered Glass Custom Taobao Store		Several layers of frosted stickers can be placed on the glass to achieve the effect of frosted glass.
Ruler	Deli Group	DL8015	The length is 1m and the division value is 1mm.
Signal generator	Dayang Science Education Taobao Store	TFG6920A	Common ones in university laboratories are available.
Vibrator	Dayang Science Education Taobao Store		The maximum amplitude is 1.5cm.The power is large enough to cause a noticeable phenomenon when the board vibrates. Otherwise, add a power amplifier.