Medição de formas do modo Chladni com um método de alavanca óptica

Resumo

Propõe-se um método simples de medir a forma do modo Chladni em uma placa elástica pelo princípio de uma alavanca óptica.

Resumo

Determinar quantitativamente o padrão Chladni de uma placa elástica é de grande interesse tanto na ciência física quanto nas aplicações de engenharia. Neste artigo, propõe-se um método de medição de formas de modo de uma placa vibratória com base em um método de alavanca óptica. Três placas de acrílico circular foram empregadas na medição sob diferentes excitações harmônicas do centro. Diferente de um método tradicional, apenas uma caneta laser comum e uma tela de luz feita de vidro moído são empregados nesta nova abordagem. A abordagem é a seguinte: a caneta laser projeta um feixe para a placa vibratória perpendicularmente, e então o feixe é refletido à tela de luz à distância, na qual um segmento de linha feito do ponto refletido é formado. Devido ao princípio da persistência da visão, o ponto de luz poderia ser lido como uma linha reta brilhante. A relação entre a inclinação da forma do modo, o comprimento do ponto de luz e a distância da placa vibratória e da tela de luz podem ser obtidas com operações algébridas. Em seguida, a forma do modo pode ser determinada integrando a distribuição da inclinação com condições de limite adequadas. As formas de modo de campo completo da placa Chladni também poderiam ser determinadas mais de forma tão simples.

Introdução

As formas do modo Chladni são de grande interesse em aplicações científicas e de engenharia. Padrões chladni são reações de ondas físicas, e pode-se ilustrar o padrão de onda com vários métodos. É um método bem conhecido para mostrar os vários modos de vibração em uma placa elástica, delineando as linhas nodais. Pequenas partículas são sempre empregadas para mostrar os padrões chladni, uma vez que podem parar nos nós onde a amplitude vibratória relativa da placa é zero, e as posições dos nós variam com o modo ressonante para formar vários padrões Chladni.

Muitos pesquisadores têm prestado atenção a vários padrões chladni, mas eles só mostram as linhas nodais das formas de modo, as formas de modo (ou seja, amplitude de vibração) entre as linhas nodais não são ilustradas. Waller investigou as vibrações livres de um círculo¹, um quadrado², um isósceles triângulos angulares retos³, um retangular⁴, placas elípticas^5, e diferentes padrões Chladni são ilustrados. Tuan et al. reconstruíram diferentes padrões chladni através de abordagens experimentais e teóricas, e a equação inhomogêneo de Helmholtz é adotada durante a modelagem teórica^6,7. É um método popular de usar o Laser Doppler Vibrometer (LDV) ou Interferometry padrão de mancha eletrônica (ESPI) para medir quantitativamente as formas de modo dos padrões Chladni^8,9,10. Embora o LDV permita a resolução de amplitude femtómetro e faixas de frequência muito altas, infelizmente, o preço do LDV também é um pouco caro para demonstração em sala de aula e/ou educação física universitária. Com essa consideração, o presente artigo propôs uma abordagem simples para determinar quantitativamente as formas de modo de um padrão Chladni de baixo custo, uma vez que apenas uma caneta laser extra e uma tela de luz são necessárias aqui.

O presente método de medição é ilustrado na Figura 1¹¹. A placa vibratória tem três posições diferentes: a posição de descanso, a posição 1 e a posição 2. As posições 1 e 2 representam os dois lugares máximos vibratórios da placa. Uma caneta laser projeta um feixe reto na superfície da placa, e se a placa se localizar na posição de descanso, o raio laser será diretamente refletido na tela de luz. Enquanto a placa se localiza na posição 1 e 2, então o raio laser será refletido para o ponto A e B na tela de luz, respectivamente. Devido ao efeito da persistência da visão, haverá uma linha reta brilhante na tela de luz. O comprimento da luz brilhante L está relacionado à distância D entre a tela de luz e a localização do ponto laser. Diferentes pontos na placa possuem inclinações diferentes, que poderiam ser determinadas pela relação entre L e D. Depois de obter a inclinação da forma do modo em diferentes pontos da placa, o problema se transforma em uma integral definitiva. Com a ajuda da amplitude de vibração de limite da placa e dos dados de inclinação discretos, a forma de modo da placa vibratória pode ser obtida facilmente. Toda a configuração experimental é dada na Figura 2¹¹.

Este artigo descreve a configuração experimental e o procedimento para o método de alavanca óptica para medir as formas do modo Chladni. Alguns resultados experimentais típicos também são ilustrados.

Protocolo

1. Configuração e procedimentos experimentais

NOTA: Configure o sistema experimental conforme mostrado na Figura 2.

1. Preparação do sistema de vibração
   1. Prepare três placas de acrílico circular espelhadas de 1,0 mm com diâmetro de 150 mm, 200 mm e 250 mm, respectivamente. Faça um orifício de 3 mm de diâmetro no centro de cada placa. Marque vários pontos pretos a cada 5 mm ao longo de um raio arbitrário.
   2. Coloque cada placa na barra de atuação do vibrador com um parafuso no ponto médio. Dirija o vibrador com uma onda seno usando um gerador de forma de onda, e as configurações padrão serão suficientes para o experimento de ressonância.
      NOTA: A direção de excitação do vibrador é horizontal para a conveniência de mover a tela depois.
   3. Aquisição da frequência de ressonância
      1. Coloque a caneta laser para projetar o raio laser na placa vibratória perpendicularmente para que o feixe seja refletido à tela de luz à distância. As distâncias entre a caneta laser e a placa e a tela de luz são de 120 mm e 500 mm, respectivamente.
         NOTA: Quanto mais distante a distância entre a tela de luz e a placa vibratória, mais óbvio aparece o fenômeno. Observa-se também que o presente método pode ser usado para medir formas de modo metricimétrico ou não-eixo. Devido à consideração da simplicidade e conveniência, o presente manuscrito apenas demonstra a aplicação na determinação de formas de modo eixosmétricos de três placas circulares. Então só precisamos medir a amplitude de vibração ao longo de qualquer direção radial para reconstruir a forma de modo bidimensional da placa.
      2. Mova a caneta laser ao longo da direção perpendicular à sua direção de comprimento para fazer o ponto de incidente escanear um diâmetro enquanto o gerador de sinal muda sua frequência continuamente. Faça-o rapidamente até que o comprimento da mancha seja significativamente estendido ao longo do diâmetro ao digitalizar em uma determinada faixa de frequência, e alguns pontos com quase nenhuma expansão aparecem. Para a placa com diâmetro de 150 mm, 200 mm e 250 mm, as faixas de frequência varridas são de 200-400 Hz, 100-300 Hz e 50-250 Hz, respectivamente.
      3. Escaneie este certo intervalo de frequência lentamente e escolha a frequência em que o local se expande mais obviamente. Verifica-se que para a placa com diâmetro de 150 mm, 200 mm e 250 mm, as frequências de ressonância são de 346 Hz, 214 Hz e 150 Hz, respectivamente.
2. Preparação do caminho leve e sistema de medição
   1. Coloque a tela de luz paralela à placa vibratória. Marque a distância com uma régua de medidor, e use 500 mm como a distância inicial.
   2. Coloque a caneta laser para projetar o feixe perpendicularmente na placa de tal forma que o feixe seja refletido à tela de luz à distância. Certifique-se de que a marca feita antes pode ser escaneada enquanto a caneta laser estiver se movendo.
      NOTA: A luz do raio laser deve ser projetada perpendicularmente na placa.
3. Medição experimental
   1. Ligue o gerador de sinal e defina a frequência de excitação como a mesma da frequência de ressonância obtida na etapa 1.1.3.3. A intensidade do sinal deve ser o menor possível, uma vez que o ponto de luz na tela de luz é grande o suficiente para ser gravado.
   2. Ajuste a caneta laser para fazer o ponto de incidente coincidir com o primeiro marcador, que é o marcador mais próximo do ponto fixo da placa.
   3. Mova a tela de uma distância D de 500 mm a 1000 mm e meça o comprimento do ponto L na tela a cada 50 mm. Registo de dados em forma tabular.
   4. Ajuste a caneta laser para fazer o ponto de incidente adjacente ao próximo marcador por sua vez e repita o passo 1.3.3 até que todos os marcadores tenham sido medidos.
      NOTA: Uma vez que as placas de acrílico são facilmente deformadas plasticamente sob excitação, o processo experimental de medição de uma placa não pode ser pausado por um longo tempo.
   5. Substitua a placa anterior pela próxima e repita as etapas 1.3.1 para 1.3.4.

2. Processamento de dados

1. Determine o ângulo φ entre o incidente e a luz refletida com a relação:
   
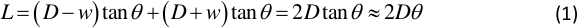
   onde D é a distância entre a posição de descanso da placa vibratória e a tela de luz, w está vibrando amplitude da placa, e L é o comprimento do ponto de luz na tela de luz. Vários pares de D e L são obtidos na etapa 1.3.3.
2. Determine a inclinação 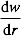da forma de modo por:
   
   NOTA: A inclinação obtida é sempre positiva com eqs. (1) e (2).
3. Use um sinal de menos entre dois pontos zero para obter a distribuição da inclinação verdadeira.
   NOTA: Não importa se a revisão começa a partir do primeiro ou do segundo ponto zero.
4. Integre a distribuição de inclinação de cada placa e determine a constante integral pelos nódulos para obter a forma do modo com:
   
   NOTA: Os nódulos correspondem à maior inclinação da forma do modo. é uma constante determinada pela localização das linhas nodais do padrão Chladni mostradas na Figura 2.
5. Calcule a incerteza da inclinação¹² com:
   
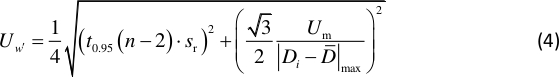
   NOTA: t_0,95(n – 2) é o fator de distribuição t com 95% de confiança e graus de liberdade n-2, e é cerca de 2 aqui. S_r é o erro padrão da regressão linear com D e L, U_m denota a incerteza da distância medida D_i, e é de 0,5 mm aqui. A distância média medida é definida por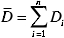 , e n denota o número total de D_imedido .

Resultados

A frequência de excitação que pode excitar o padrão de Chladni eixos é determinada através do teste de varredura de frequência. Três placas de acrílico circular com diâmetros de 150 mm, 200 mm e 250 mm são testadas, e os resultados mostram que as primeiras frequências de ressonância mesmétricas do eixo de primeira ordem são de 346 Hz, 214 Hz e 150 Hz para as três placas, respectivamente. Conclui-se que, com maior diâmetro, a placa é mais flexível, e a frequência de ressonância correspondente será me...

Discussão

O método de alavanca óptica é adotado neste artigo para determinar a forma de modo de uma placa, uma vez que o padrão Chladni só pode mostrar as linhas nodais de uma placa vibratória. Para determinar a forma do modo da placa, a relação entre a inclinação e a distância da tela de luz e o comprimento do ponto deve ser obtida com antecedência. Então, através do cálculo de integração definitivo, a forma de modo do padrão Chladni poderia ser quantitativamente determinada.

Geralmen...

Materiais

Name	Company	Catalog Number	Comments
Acrylic plates	Dongguan Jinzhu Lens Products Factory		Three 1.0-mm-thickness mirrored circular acrylic plates with diameter of 150 mm, 200 mm and 250 mm respectively. They are easily deformed.
Laser pen	Deli Group	2802	Red laser is more friendly to the viewer. The finer the laser beam, the better.
Light screen	Northern Tempered Glass Custom Taobao Store		Several layers of frosted stickers can be placed on the glass to achieve the effect of frosted glass.
Ruler	Deli Group	DL8015	The length is 1m and the division value is 1mm.
Signal generator	Dayang Science Education Taobao Store	TFG6920A	Common ones in university laboratories are available.
Vibrator	Dayang Science Education Taobao Store		The maximum amplitude is 1.5cm.The power is large enough to cause a noticeable phenomenon when the board vibrates. Otherwise, add a power amplifier.