Finite-Elemente-Modellierung einer zellulären elektrischen Mikroumgebung

Zusammenfassung

Dieser Artikel stellt eine Strategie zum Erstellen von Finite-Elemente-Modellen von faserigen leitfähigen Materialien vor, die einem elektrischen Feld (EF) ausgesetzt sind. Die Modelle können verwendet werden, um den elektrischen Input abzuschätzen, den Zellen, die in solchen Materialien ausgesät sind, erhalten, und die Auswirkungen der Änderung der Materialeigenschaften, der Struktur oder der Ausrichtung des Gerüsts zu bewerten.

Zusammenfassung

Klinische Studien zeigen, dass elektrische Stimulation (ES) eine potenzielle Therapie für die Heilung und Regeneration verschiedener Gewebe ist. Das Verständnis der Mechanismen der Zellantwort bei Exposition gegenüber elektrischen Feldern kann daher die Optimierung klinischer Anwendungen leiten. In-vitro-Experimente zielen darauf ab, diese aufzudecken, und bieten den Vorteil breiterer Input- und Output-Bereiche, die ethisch und effektiv bewertet werden können. Die Fortschritte bei In-vitro-Experimenten sind jedoch schwer direkt in klinischen Umgebungen zu reproduzieren. Das liegt vor allem daran, dass sich die in vitro verwendeten ES-Geräte deutlich von denen unterscheiden, die für den Patientengebrauch geeignet sind, und der Weg von den Elektroden zu den Zielzellen ist unterschiedlich. Die Übersetzung der In-vitro-Ergebnisse in In-vivo-Verfahren ist daher nicht einfach. Wir betonen, dass die Struktur und die physikalischen Eigenschaften der zellulären Mikroumgebung eine entscheidende Rolle bei den tatsächlichen experimentellen Testbedingungen spielen und schlagen vor, dass Messungen der Ladungsverteilung verwendet werden können, um die Lücke zwischen in vitro und in vivo zu schließen. Vor diesem Fall zeigen wir, wie in silico Finite-Elemente-Modellierung (FEM) verwendet werden kann, um die zelluläre Mikroumgebung und die Veränderungen zu beschreiben, die durch die Exposition gegenüber elektrischen Feldern (EF) erzeugt werden. Wir zeigen, wie der EF mit geometrischer Struktur gekoppelt wird, um die Ladungsverteilung zu bestimmen. Wir zeigen dann den Einfluss zeitabhängiger Eingaben auf die Ladungsbewegung. Schließlich demonstrieren wir die Relevanz unserer neuen In-silico-Modellmethodik anhand von zwei Fallstudien: (i) in vitro fibrous Poly(3,4-ethylendioxythiophen)poly(styrolesulfonate) (PEDOT-PSS) Gerüste und (ii) in vivo Kollagen in extrazellulärer Matrix (ECM).

Einleitung

ES ist die Verwendung von EFs mit dem Ziel, biologische Zellen und Gewebe zu kontrollieren. Sein Mechanismus basiert auf dem physikalischen Reiz, der an die Zelle weitergegeben wird, wenn die Biomoleküle in und um sie herum einem extern erzeugten Spannungsgradienten ausgesetzt sind. Geladene Teilchen sind in einer organisierten Bewegung nach dem Coulomb-Gesetz beteiligt und erzeugen Schleppkräfte auf die ungeladenen Teilchen. Der resultierende Flüssigkeitsfluss und die Ladungsverteilung verändern Zellaktivitäten und -funktionen wie Adhäsion, Kontraktion, Migration, Orientierung, Differenzierung und Proliferation^1, während die Zelle versucht, sich an die Veränderung der Mikroumgebungsbedingungen anzupassen.

Da EFs kontrollierbar, nicht-invasiv, nicht pharmakologisch sind und nachweislich einen wirksamen Einfluss auf das essentielle Zellverhalten haben, ist ES ein wertvolles Werkzeug für das Tissue Engineering und die regenerative Medizin. Es wurde erfolgreich verwendet, um neuronale², Skelett³, Herzmuskel⁴, Knochen⁵ und Haut⁶ Entwicklung zu steuern. Darüber hinaus wird es, da es die Iontophorese⁷verstärkt, als alternative oder ergänzende Behandlung zu herkömmlichen pharmakologischen Behandlungen eingesetzt. Seine Effizienz bei der Schmerzbehandlung wird immer noch diskutiert, da qualitativ hochwertigere klinische Studien erwartet werden^8,9,10. Dennoch wurden keine Nebenwirkungen berichtet und es hat das Potenzial, das Wohlergehen der Patienten zu verbessern^{11,12,13,14,15}.

Während nur klinische Studien ein endgültiges Urteil über die Wirksamkeit eines Verfahrens abgeben können, sind In-vitro- und In-silico-Modelle erforderlich, um das Design einer vorhersagbaren ES-Behandlung zu beeinflussen, da sie eine stärkere Kontrolle über ein breiteres Spektrum von experimentellen Bedingungen bieten. Die untersuchten klinischen Anwendungen von ES sind Knochenregeneration^16,17, Wiederherstellung der denervated Muskeln^18,19, axonale Regeneration nach der Operation^20,21, Schmerzlinderung²², Wundheilung^23,24,25 und iontophoretische Arzneimittelabgabe²⁶. Damit ES-Geräte in allen möglichen Zielanwendungen weit verbreitet werden können, müssen klinische Studien noch stärkere Beweise für eine effiziente Behandlung liefern. Selbst in Bereichen, in denen sowohl In-vivo-Tier- als auch Humanstudien durchweg positive Ergebnisse melden, hält die große Anzahl der berichteten Methoden in Verbindung mit zu wenig Anleitung zur Wahl zwischen ihnen und einem hohen Anschaffungspreis Kliniker davon ab, in ES-Geräte zu investieren²⁷. Um dies zu überwinden, kann das Zielgewebe nicht mehr als BlackBox behandelt werden (Grenze der In-vivo-Experimente), sondern muss als komplexe Synergie mehrerer Subsysteme gesehen werden (Abbildung 1).

Mehrere ES-Experimente wurden in vitro in den Jahren^{28,29,30,31,32,33,34}durchgeführt. Die meisten von ihnen charakterisieren die ES nur durch den Spannungsabfall zwischen den Elektroden geteilt durch den Abstand zwischen ihnen - eine grobe Annäherung an die elektrische Feldgröße. Das elektrische Feld selbst beeinflusst jedoch nur geladene Teilchen, nicht Zellen direkt. Wenn mehrere Materialien zwischen dem Gerät und den Zellen liegen, kann die grobe Annäherung nicht halten.

Eine bessere Charakterisierung des Eingangssignals erfordert einen klaren Überblick darüber, wie der Reiz an die Zelle übertragen wird. Hauptmethoden zur Lieferung von ES sind direkte, kapazitive und induktive^{Kopplung 35,36}. Die Geräte für jedes Verfahren unterscheiden sich je nach Elektrodentyp (Stab, Planar oder Wicklung) und Platzierung relativ zum Zielgewebe (in Kontakt oder isoliert)³⁵. Geräte, die in vivo für längere Behandlungen verwendet werden, müssen tragbar sein, daher werden die Elektroden und meistens die Energiequelle entweder implantiert oder als Wundauflagen oder elektroaktive Pflaster an der Haut befestigt. Der erzeugte Spannungsgradient verdrängt geladene Teilchen im Behandlungsbereich.

Da sie den resultierenden geladenen Teilchenfluss in der Nähe der Zellen beeinflusst, ist die Gerüststruktur bei der Gestaltung von ES-Protokollen von größter Bedeutung. Unterschiedliche Ladungstransportkonfigurationen entstehen, wenn sich das Plattformmaterial, die Synthesetechnik, die Struktur oder die Orientierung relativ zum Spannungsgradienten ändern. In vivo wird die Verfügbarkeit und Bewegung geladener Teilchen nicht nur von Zellen beeinflusst, sondern auch vom Kollagennetzwerk und der interstitiellen Flüssigkeit, aus der das unterstützende ECM besteht. Engineered Gerüste werden zunehmend verwendet, um natürliche Zellmikroumgebungen in vitro besser nachzubilden^1,35. Gleichzeitig ist das ECM ein komplexes natürliches Gerüst.

Künstliche Gerüste basieren auf Metallen, leitenden Polymeren und Kohlenstoff, die mit dem Fokus auf die Balance zwischen Biokompatibilität und elektrochemischer Leistung und Langzeitstabilität^{entwickelt wurden 36}. Ein vielseitiger Gerüsttyp ist die elektrosponnene Fasermatte, die eine steuerbare nanoskalige Topographie bietet. Dies kann so konstruiert werden, dass es dem ECM ähnelt und somit ähnliche mechanische Hinweise liefert, die die Regeneration einer Vielzahl von Geweben unterstützen³⁷. Um ES signifikant zu beeinflussen, müssen die Matten bis zu einem gewissen Grad leitfähig sein. Leitfähige Polymere sind jedoch schwer zu elektrospinnen und das Mischen mit isolierenden Trägern begrenzt die Leitfähigkeit der resultierenden^{Fasern 38}. Eine Lösung ist die Polymerisation eines leitfähigen Monomers auf der Oberfläche einer dielektrischen Faser, was zu einer guten mechanischen Festigkeit und elektrischen Eigenschaften des Endprodukts^{führt 38}. Ein Beispiel ist die Beschichtung von Elektrosponnfasern aus Seide mit dem halbleitenden PEDOT-PSS^39. Die Kombination von mechanischen und elektromagnetischen Hinweisen beschleunigt das Neuritenwachstum signifikant^40,41,42. Neurite folgen der Ausrichtung der Gerüstfasern und verlängern sich mehr nach Einwirkung eines EF parallel zu den Fasern als eines vertikalen^43. In ähnlicher Weise fördert die Ausrichtung von faserigen Gerüsten auf die EF auch die myogene^{Reifung 33}.

Das ECM besteht hauptsächlich aus faserbildenden Proteinen⁴⁴, von denen Kollagen Typ I der Hauptbestandteil in allen tierischen Geweben außer Knorpel (reich an Kollagen Typ II)⁴⁴ist. Tropokollagen (TC), dreifache helikale Konformation von Polypeptidsträngen, ist das Strukturmotiv der Kollagenfibrillen⁴⁵. Transmissionselektronenmikroskopische und rasterkraftmikroskopische Bilder von Kollagenfibrillen zeigen ein D-periodisches Bandmuster^46, das vom Hodge & Petruska-Modell⁴⁷ als regelmäßige Arrays von TC-Lücken und -Überlappungen⁴⁵erklärt wird. Sehnen bestehen aus einer ausgerichteten kollagenen Fibrillenmatrix, die durch eine nicht-kollagene hochhydrophile Proteoglykanmatrix abgeschirmt ist^48,49. Decorin ist ein kleines leucinreiches Proteoglykan (SLRP), das in der Lage ist, die Lückenregionen von Kollagenfibrillen zu binden und sich mit anderen SLRPs über ihre Glykosaminoglykan-Seitenketten (GAG) zu verbinden⁴⁹. Studien an Sehnen zeigen, dass sich ihre elektrischen Eigenschaften signifikant ändern, wenn sie hydratisiert werden^50,51, Ladungstransportmechanismus, der sich von protonisch zu ionisch ändert, wenn der Hydratationsgrad steigt⁵¹. Dies deutet darauf hin, dass die elektrische Leitung entlang einer Kollagen-Typ-I-Fibriere durch eine Decorin-Wasserschicht ermöglicht werden könnte, wobei Spalt- und Überlappungsbereiche unterschiedliche elektrische Leitfähigkeiten und Dielektrizitätskonstanten aufweisen.

Da eine identische Nachbildung des ECM durch künstliche Gerüste unwahrscheinlich ist, scheint sich das Wissen, das Synergien zwischen in vivo und in vitro erzeugt, die durch übersetzbare Ergebnisse ermöglicht werden, in einer Sackgasse zu befindet. Die In-silico-Modellierung ermöglicht nicht nur die Übersetzung zwischen den beiden, sondern bietet auch wichtige Vorteile bei der Charakterisierung der unbekannten Prozesse, die an ES beteiligt sind. Der Vergleich der In-vivo-Beobachtungen mit den In-vitro-Beobachtungen kann Aufschluss über die Kopplungsstärke zwischen dem Zielgewebe und dem Rest des Organismus geben, deckt aber keine aktuellen Wissensgrenzen auf. Das Unbekannte kann aufgedeckt werden, indem der Unterschied zwischen dem, was auf der Grundlage des aktuellen Wissens erwartet wird, und dem, was passiert, beobachtet wird. In-silico-Experimente, die auf mathematischer Modellierung basieren, ermöglichen die Aufteilung des Prozesses in bekannte und unbekannte Teilprozesse. Auf diese Weise kommen Phänomene zum Vorschein, die im Modell nicht berücksichtigt werden, wenn in silico Vorhersagen mit in vitro und in vivo Experimenten verglichen werden.

Die Bildung und Prüfung von Hypothesen über die zugrunde liegenden Mechanismen, wie Zellen und Gewebe von elektrischen Feldern beeinflusst werden, wird durch die große Anzahl von Parametern⁵² behindert, die separat getestet werden müssen. Um repräsentative experimentelle Bedingungen zu definieren, muss der ES-Prozess in Teilprozesse aufgeteilt werden (Abbildung 1) und dominante Eingangssignale, die das Zellverhalten beeinflussen, müssen identifiziert werden. Modelle, die grundlegende physikalische Effekte von ES auf Zellen darstellen, beschreiben die Domäne, die das EF mit der Zelle koppelt - die der geladenen Teilchen⁵³. Das Verhalten von Partikeln außerhalb der Zelle hängt von der Mikroumgebung ab und kann getrennt von der Zelle untersucht werden. Das dominante Eingangssignal für die Zelle ist die Teilmenge der ES-Geräteausgänge, die den größten Grad an Variabilität in der Zellantwort verursacht. Die kleinste Teilmenge der vollständigen experimentellen Parameter, die Variationen in allen dominanten Zelleingangssignalen erzeugen kann, kann verwendet werden, um die Parameterraumdimension und die Anzahl der Testfälle zu verringern.

Die Eingabe des biologischen ES-Zielmodells muss eine Teilmenge der vom ES-Gerät erzeugten Ausgangssignale sein, die zur Beschreibung der physikalischen Auswirkungen von ES auf Zellen nützlich sind. Ein einfacher Bioreaktor mit direkter Kopplung hat die gleiche Struktur wie elektrolytische elektrochemische Zellen. Modelle von diesen zeigen die primäre (Berücksichtigung des Lösungswiderstands), sekundäre (auch faradische Reaktionen berücksichtigende) oder tertiäre (auch für ionendiffusion berücksichtigende) Stromdichteverteilung. Da Komplexität in Rechenkosten übersetzt wird, eignet sich das einfachste Modell am besten für die Erforschung von Parametern im Weltraum. Simulationen von Faserverbundwerkstoffen, die durch Materialeigenschaften motiviert sind^54, konzentrieren sich auf Schüttguteigenschaften als Folge einer komplexen Mikroarchitektur und können daher lokale Auswirkungen der EF-Exposition nicht beschreiben. Bestehende in silico-Modelle, motiviert durch ES, konzentrieren sich auf die biologische Probe, sei es eine einzelne Zelle, die in ein homogenes Medium^55,56,57eingetaucht ist, oder komplexe Gewebe mit homogenem extrazellulärem Raum⁵⁸. Ladungs- und Stromdichte (Abbildung 2) können als Schnittstellensignale zwischen Modellen des ES-Geräts und der biologischen Probe oder zwischen verschiedenen Komponenten des ES-Geräts fungieren. Das vorgeschlagene FEM-basierte Protokoll verwendet die in Abbildung 2 beschriebenen Gleichungen und wurde verwendet, um zu untersuchen, wie gerüstabhängige Parameter verwendet werden können, um diese beiden Signale unabhängig von dem EF zu modulieren, der durch einen direkten Kopplungsaufbau erzeugt wird. Die Ergebnisse unterstreichen, dass es notwendig ist, die elektrischen Eigenschaften von Gerüsten oder ECM zu berücksichtigen, wenn untersucht wird, wie sich ES auf Zielzellen auswirkt.

Protokoll

1. Erstellen Sie das Modell in COMSOL

1. Öffnen Sie COMSOL und wählen Sie Leeres Modell.
2. Parameter: Klicken Sie im Modellgeneratormit der rechten Maustaste auf Globale Definitionen,wählen Sie Parameteraus, und fügen Sie Parameter gemäß Tabelle 1hinzu.
3. Materialien: Fügen Sie Materialien mit Eigenschaften gemäß Tabelle 2hinzu.
   1. Klicken Sie im Modellgenerator unter Globale Definitionenmit der rechten Maustaste auf Material, und wählen Sie Leeres Material aus.
   2. Materialeigenschaften hinzufügen: Erweitern Sie in den Einstellungen des neu hinzugefügten Materials Materialeigenschaften > Grundlegende Eigenschaften,wählen Sie Relative Permittivität und drücken Sie das Symbol '+', um eine Eigenschaft hinzuzufügen. Wiederholen Sie den Schritt für Elektrische Leitfähigkeit.
   3. Geben Sie im Materialinhaltdie aktuellen Materialeigenschaften gemäß Tabelle 2 ein.
4. Komponentendefinition: Klicken Sie auf der Registerkarte Start des oberen Menübands mit der linken Maustaste auf Komponente hinzufügen, und wählen Sie 3Daus. Im Modellgeneratorwird ein neuer Komponentenknoten angezeigt.
5. Geometrie: Klicken Sie im Modellgeneratormit der rechten Maustaste auf Geometrie, klicken Sie mit der linken Maustaste auf Einfügen, doppelklicken Sie auf das vollständige Modell und wählen Sie die entsprechende Sequenz (SC/SNC/RC/RNC/RNCd).
6. Alternativ können Sie die Geometrie nach den untergeordneten Schritten von Grund auf neu erstellen.
   1. Klicken Sie im Modell-Generatorunter dem aktuellen Komponentenknoten mit der linken Maustaste auf Geometrie. Derselbe Geometrieknoten wird in den folgenden untergeordneten Schritten verwiesen. Ändern Sie im Fenster Einstellungen die Längeneinheit in nm und stellen Sie sicher, dass "Werte beim Ändern von Einheiten skalieren" deaktiviert ist.
   2. Geometrie des Gerüsts
      1. Klicken Sie im Modell-Generatormit der rechten Maustaste auf Geometrie und wählen Sie Blockieren.
      2. Geben Sie auf der Registerkarte Einstellungen die Bezeichnung "Gerüstausdehnungen" ein.
      3. Erweitern Sie Größe und Form und geben Sie "Ws", "Ls", "Hs" für Breite, Tiefe und Höhe ein.
      4. Erweitern Sie Position, und ändern Sie die Basis in Center.
      5. Erweitern Sie Auswahl der resultierenden Elemente,wählen Sie Neu und fügen Sie "Gerüstauswahl" hinzu.
   3. Ausdehnungen der umgebenden Substanz: Klicken Sie im Modell-Generatorunter Geometriemit der rechten Maustaste auf Gerüstausdehnungen, wählen Sie Duplizierenaus, und bearbeiten Sie die Registerkarte Einstellungen.
      1. Ändern Sie die Bezeichnung in "Medienausdehnungen".
      2. Fügen Sie zu jedem Feld im Abschnitt Größe und Shape "med_ratio *" vor dem vorhandenen Parameter hinzu.
      3. Fügen Sie unter Auswahl der resultierenden Elementedie neue Auswahl als "Medienauswahl" hinzu.
   4. Geometrie einer Faser (SC springt zu 1.6.6)
      1. Core (RC springt zu 1.6.4.2)
         1. Klicken Sie im Modell-Generatormit der rechten Maustaste auf Geometrie, wählen Sie Zylinder, und bearbeiten Sie die Registerkarte Einstellungen wie folgt.
         2. Ändern Sie die Bezeichnung in "Core".
         3. Erweitern Sie Größe und Form und geben Sie "Rc" und "Lf" für Radius und Höhe ein.
         4. Erweitern Sie Position und geben Sie "-excess*Ws/2" und "-Lf/2" für x und y ein.
         5. Erweitern Sie Achse, und ändern Sie den Achsentyp in y-Achse.
         6. Erweitern Sie Auswahl der resultierenden Entitäten und fügen Sie "Kernauswahl" hinzu.
      2. Coat (SNC springt zu 1.6.5)
         1. Slab (RC oder RNC überspringen Sie zu 1.6.4.2.2; RNCd springt zu 1.6.4.2.3)
            1. Klicken Sie im Modell-Generator unter Geometriemit der rechten Maustaste auf Gerüstausdehnungen, und wählen Sie Duplizierenaus. Stellen Sie sicher, dass das Duplikat (Gerüstausdehnungen 1) direkt nach Kern in der Geometriesequenz kommt.
            2. Ändern Sie auf der Registerkarte Einstellungen die Bezeichnung in "Coat".
            3. Erweitern Sie auf der Registerkarte Einstellungen die Option Auswahl der resultierenden Elemente und erstellen Sie "Faserauswahl".
            4. Fahren Sie mit 1.6.5.
         2. Gleichartig
            1. Klicken Sie im Modell-Generator mit der rechten Maustaste auf Geometrie, wählen Sie Zylinder und bearbeiten Sie die Registerkarte Einstellungen wie folgt.
            2. Ändern Sie die Beschriftung in "Coat".
            3. Erweitern Sie Größe und Form und geben Sie "Rf" und "Lf" für Radius und Höhe ein.
            4. Erweitern Sie Position und geben Sie "-excess*Ws/2" und "-Lf/2" für x und y ein.
            5. Erweitern Sie Achse und ändern Sie den Achsentyp in y-Achse (RC springt zu 1.6.4.2.2.7).
            6. Erweitern Sie Ebenen,füllen Sie "Rf-Rc" für Dicke aus und lassen Sie nur "Ebenen auf der Seite" aktiviert.
            7. Erweitern Sie Auswahl der resultierenden Elemente und fügen Sie "Coat Selection" oder für RC "Fiber Selection" hinzu (RC springt zu 1.6.5).
            8. Klicken Sie im Modell-Generatormit der rechten Maustaste auf Geometrie , und wählen Sie Elemente löschenaus.
            9. Ändern Sie auf der Registerkarte Einstellungen die geometrische Einstiegsebene in Domäne und wählen Sie Mantelauswahl für Auswahl aus.
            10. Entfernen Sie alle Domänen außer Domäne 3 aus dem Auswahlfeld (dem Kern des mehrschichtigen Zylinders).
            11. Erweitern Sie Auswahl der resultierenden Elemente, und wählen Sie Mantelauswahl aus.
            12. Fahren Sie mit 1.6.5.
         3. Periodisches Array von zwei Typen
            1. Klicken Sie im Modell-Generator mitder rechten Maustaste auf Geometrie, und wählen Sie Zylinderaus. Klicken Sie mit der rechten Maustaste auf das neu erstellte Element, und wählen Sie Duplizierenaus. Bearbeiten Sie die Registerkarte Einstellungen wie folgt.
               1. Setzen Sie Label auf "Coat 1" / "Coat 2".
               2. Legen Sie radius auf Rf fest.
               3. Stellen Sie die Höhe auf "D*prop"/"D*(1-prop)" ein.
               4. Erweitern Sie die Position und geben Sie "-excess*Ws/2" für x und "-Lf/2"/"-Lf/2+D*prop" auf y ein.
               5. Erweitern Sie Achse, und ändern Sie den Achsentyp in Y-Achse.
               6. Erweitern Sie den Abschnitt Ebenen und füllen Sie "Rf-Rc" aus. Stellen Sie sicher, dass nur das Kontrollkästchen "Ebenen auf der Seite" aktiviert ist.
               7. Erweitern Sie Auswahl der resultierenden Elemente und erstellen Sie "Coat 1 Selection"/ "Coat 2 Selection".
            2. Klicken Sie im Modell-Generatormit der rechten Maustaste auf Geometrie , und wählen Sie Elemente löschenaus.
               1. Ändern Sie auf der Registerkarte Einstellungen die geometrische Einstiegsebene in Domäne und wählen Sie im Arbeitsfenster Zylinder 2 (cyl2) und Zylinder 3 (cyl3) aus.
               2. Entfernen Sie alle Domänen außer Domäne 3 aus dem Auswahlfeld (dem Kern der geschichteten Zylinder).
               3. Erweitern Sie Auswahl der resultierenden Elemente, und erstellen Sie Mantelauswahl.
            3. Klicken Sie im Modell-Generatormit der rechten Maustaste auf Geometrie, erweitern Sie Transformationen, und wählen Sie Arrayaus. Bearbeiten Sie die Registerkarte Einstellungen wie folgt.
               1. Wählen Sie "Coat Selection" für Eingabeobjekte.
               2. Legen Sie den Array-Typ auf Linear fest.
               3. Stellen Sie Größe auf "Lf/D" ein.
               4. Setzen Sie Verschiebung auf y-Achse auf "D".
   5. Geometrie eines orientierten Faserarrays
      1. Core Array (RC springt zu 1.6.5.2)
         1. Klicken Sie im Modell-Generatormit der rechten Maustaste auf Geometrie, Transformieren erweitern , und wählen Sie Drehen.
            1. Aktivieren Sie auf der Registerkarte Einstellungen den Schalter für Eingabeobjekte, und wählen Sie Kernauswahl aus der Dropdown-Liste aus. Stellen Sie sicher, dass das Kontrollkästchen Eingabeobjekte behalten nicht aktiviert ist.
            2. Erweitern Sie Drehwinkel und füllen Sie "theta" für Rotation aus.
            3. Erweitern Sie Auswahl der resultierenden Elemente und erstellen Sie "Faserauswahl".
         2. Klicken Sie im Modell-Generator mit der rechten Maustaste auf Geometrie, Erweitern Sie Transformationen, und wählen Sie Array(
            1. Ändern Sie die Bezeichnung in "Core Array".
            2. Wählen Sie Kernauswahl in der Dropdown-Liste für Eingabeobjekte aus.
            3. Erweitern Sie Größe,ändern Sie den Array-Typ in Linear und geben Sie "n_1*(theta<=45) +n_2*(theta>45)" für Größe ein.
            4. Erweitern Sie Verschiebung und geben Sie "2*tes*Rc*cos(theta)", "2*tes*Rc*sin(theta)" für x und y ein.
            5. Erweitern Sie Auswahl der resultierenden Elemente und wählen Sie "Faserauswahl".
      2. Coat Array (SNC springt zu 1.6.5.3)
         1. Klicken Sie im Modell-Generatormit der rechten Maustaste auf Geometrie, Transformieren erweitern , und wählen Sie Drehen.
            1. Aktivieren Sie auf der Registerkarte Einstellungen den Schalter Eingabeobjekte und wählen Sie Coat Selection aus der Dropdown-Liste. Stellen Sie sicher, dass "Eingabeobjekte behalten" nicht aktiviert ist.
            2. Erweitern Sie Drehwinkel und füllen Sie "theta" für Rotation aus.
            3. Erweitern Sie Auswahl der resultierenden Elemente und wählen Sie "Faserauswahl".
         2. Klicken Sie im Modell-Generatormit der rechten Maustaste auf Geometrie, Transformieren erweitern , und wählen Sie Array(
            1. Ändern Sie die Bezeichnung in "Coat Array".
            2. Wählen Sie in der Dropdown-Liste für Eingabeobjekte die Option Mantelauswahl aus.
            3. Erweitern Sie Größe,ändern Sie den Array-Typ in Linear und geben Sie "n_1*(theta<=45) +n_2*(theta>45)" für Größe ein.
            4. Erweitern Sie Verschiebung und geben Sie "2*tes*Rc*cos(theta)", "2*tes*Rc*sin(theta)" für x und y ein.
            5. Erweitern Sie Auswahl der resultierenden Elemente und wählen Sie "Faserauswahl".
      3. Geschnittenes Gerüst
         1. Verbindungslinien vereinen: Klicken Sie im Modell-Generator mit der rechten Maustaste auf Geometrie, Boolesche Werte und Partitionen erweitern, und wählen Sie Unionaus.
            1. Ändern Sie die Bezeichnung in "Fasern".
            2. Aktivieren Sie den Schalter Eingabeobjekte, und wählen Sie Faserauswahl aus der Dropdown-Liste aus.
            3. Stellen Sie sicher, dass das Kontrollkästchen "Eingabeobjekte behalten" nicht aktiviert ist.
            4. Stellen Sie sicher, dass "Innere Grenzen beibehalten" aktiviert ist.
            5. Erweitern Sie Auswahl der resultierenden Elemente und wählen Sie Gerüstauswahl aus der Dropdown-Liste aus.
         2. Schnitt ausführen: Klicken Sie im Modellgenerator mit der rechten Maustaste auf Geometrie, erweitern Sie Boolesche Werte und Partitionen, und wählen Sie Schnittmengeaus.
            1. Ändern Sie die Bezeichnung in "Gerüst".
            2. Aktivieren Sie den Schalter Eingabeobjekte und wählen Sie Gerüstauswahl aus der Dropdown-Liste aus.
            3. Stellen Sie sicher, dass das Kontrollkästchen "Eingabeobjekte behalten" nicht aktiviert ist.
            4. Stellen Sie sicher, dass "Innere Grenzen beibehalten" aktiviert ist.
   6. Ensemble-Geometrie
      1. Definieren Sie die umgebende Substanzgeometrie.
         1. Klicken Sie im Modell-Generatormit der rechten Maustaste auf Geometrie, erweitern Sie Boolesche Werte und Partitionen, und wählen Sie Differenzaus. Fahren Sie mit der Registerkarte Einstellungen fort.
         2. Wählen Sie in der Dropdownliste Hinzuzufügene Objekte die Option Medienauswahl aus.
         3. Wählen Sie in der Dropdownliste Zu subtrahierende Objekte die Option Gerüstauswahl aus.
         4. Stellen Sie sicher, dass die Kontrollkästchen "Eingabeobjekte beibehalten" und "Innere Grenzen beibehalten" aktiviert sind.
      2. Feld Medienausdehnungen löschen.
         1. Klicken Sie im Modell-Generatormit der rechten Maustaste auf Geometrie , und wählen Sie Elemente löschenaus. Fahren Sie mit der Registerkarte Einstellungen fort.
         2. Wählen Sie in der Dropdown-Liste Geometrische Einstiegsebene die Option Domäne aus.
         3. Wählen Sie in der Dropdown-Liste Auswahl die Option Medienauswahl aus.
         4. Entfernen Sie "dif1" aus dem Auswahlfeld.
   7. Build-Geometrie
      1. Stellen Sie unter dem Knoten Geometrie sicher, dass das letzte Element vor dem Knoten Kumulative Auswahlen Formularunion und nicht Formularbaugruppeist. Klicken Sie bei Bedarf mit der rechten Maustaste auf Formularbaugruppe, und ändern Sie Aktion auf der Registerkarte Einstellungen in "Vereinigung bilden".
      2. Klicken Sie im Modell-Generatormit der linken Maustaste auf Geometrie, und wählen Sie Alle erstellenaus.
7. Materialien
   1. Klicken Sie im Modell-Generator unter dem Knoten Aktuelle Komponente mit der rechten Maustaste auf Materialien, und wählen Sie Materialverknüpfungaus.
   2. Wiederholen Sie den Abschnitt fünfmal, denn je nach Komplexitätsgrad werden so viele Materialien berücksichtigt.
   3. Ordnen Sie Materialien für jede Komponente in der folgenden Reihenfolge zu: umgebende Substanz, Schichten, Kerne.
   4. Wählen Sie auf der Registerkarte Einstellungen in der Dropdown-Liste Auswahl die Option Medien/Gerüst (für SC, SNC, RC)/Coat/Core Selection aus.
   5. Erweitern Sie die Link-Einstellungen und wählen Sie das entsprechende Material aus der Dropdown-Liste aus.
8. Verwickelnd
   1. Klicken Sie im Modell-Generatormit der linken Maustaste auf den Knoten Netz unter der aktuellen Komponente.
   2. Wählen Sie auf der Registerkarte Einstellungen in der Dropdown-Liste Elementgröße die Option Normal aus, und klicken Sie mit der linken Maustaste auf Alle erstellen.
9. Physik: Klicken Sie im Modellgeneratormit der linken Maustaste auf aktuelle Komponente, wählen Sie Physik hinzufügen, erweitern Sie das AC/DC-Modul auf der Registerkarte Physik hinzufügen, wählen Sie das Modul Elektrische Ströme (ec) aus und klicken Sie auf Zu Komponente hinzufügen.
   1. Randbedingungen: Wählen Sie auf der Registerkarte Grafiken die xy-Ansicht aus.
      1. Masse: Klicken Sie im Modellgenerator mitder rechten Maustaste auf den Knoten Elektrische Ströme und wählen Sie Masse.
      2. Stellen Sie sicher, dass der Auswahlschalter für die Berandungsauswahl aktiv ist, und klicken Sie mit der linken Maustaste auf die höchste umgebende Substanzfläche parallel zur xz-Ebene, um Berandung 5 im Feld Berandungsauswahlhinzuzufügen.
      3. Terminal: Klicken Sie im Model Buildermit der rechten Maustaste auf den Knoten Elektrische Ströme und wählen Sie Terminal.
      4. Stellen Sie sicher, dass der Auswahlschalter für die Berandungsauswahl aktiv ist, und klicken Sie mit der linken Maustaste auf die unterste umgebende Substanzfläche parallel zur xz-Ebene, um Berandung 2 im Feld Berandungsauswahl hinzuzufügen.
      5. Erweitern Sie den Abschnitt Terminal und wählen Sie Spannung in der Dropdown-Liste Klemmentyp aus. Füllen Sie V0 für Spannung aus.
   2. Fügen Sie bei Bedarf Komplexität hinzu: Speichern Sie die aktuelle Komponente und kehren Sie zu Schritt 1.4 zurück, um einem anderen Komplexitätspfad zu folgen (SC / SNC / RC / RNCd).

2. Simulation durchführen

1. Adaptive Mesh-Verfeinerung
   1. Klicken Sie in Model Buildermit der linken Maustaste auf den Modellstammknoten, und wählen Sie Studie hinzufügen aus, um die Registerkarte Studie hinzufügen zu öffnen, wählen Sie Stationäre Studie aus, und klicken Sie mit der rechten Maustaste auf die Schaltfläche Studie hinzufügen.
   2. Erstellen Sie einen Studienschritt für jede erstellte Komponente: Klicken Sie unter Studienknoten mit der rechten Maustaste auf Schritt1: Stationäre Studie, und wählen Sie Duplizierenaus.
   3. Ändern Sie für jeden Studienschritt die Registerkarte Einstellungen mit den Details der entsprechenden Komponente.
      1. Erweitern Sie Physik und Variablenauswahl; In der Spalte Lösen für lassen Sie nur die aktuelle Komponente aktiviert.
      2. Erweitern Sie Studienerweiterungen, und aktivieren Sie das Kontrollkästchen Adaptive Netzverfeinerung.
      3. Wählen Sie die Geometrie der aktuellen Komponente aus der Dropdown-Liste neben Anpassung in Geometrie aus.
   4. Klicken Sie im Modellgenerator mit der rechten Maustaste auf Studie 1, und wählen Sie Berechnenaus. Dadurch werden angepasste Netze für alle Geometrien der Bauteile mit ihrem aktuellen Orientierungswinkel erzeugt.
2. Legen Sie den Orientierungswinkel fest und führen Sie eine stationäre Studie durch.
   1. Klicken Sie im Modellgeneratorunter Globale Definitionenmit der linken Maustaste auf Parameter, und ändern Sie den Parameter Theta in den für die Simulation gewünschten Faserorientierungswinkel.
   2. Erweitern Sie für jede Komponente im Modell-Generator den Knoten der Komponente, klicken Sie mit der rechten Maustaste auf Geometrie, und wählen Sie Alle erstellenaus.
   3. Klicken Sie im Modell-Generatormit der rechten Maustaste auf die Adaptive Mesh-Verfeinerungsstudie, und wählen Sie Computeaus.
   4. Klicken Sie im Modell-Generator mit der linken Maustaste auf den Modellstammknoten, und wählen Sie Studie hinzufügen aus, um die Registerkarte Studie hinzufügen zu öffnen, wählen Sie Stationäre Studie aus, und klicken Sie mit der rechten Maustaste auf die Schaltfläche Studie hinzufügen.
   5. Klicken Sie im Modell-Generatorunter der neu hinzugefügten Studie mit der linken Maustaste auf Schritt 1, erweitern Sie die Netzauswahl, und wählen Sie für jede Komponente die in der adaptiven Netzverfeinerungsstudie generierten Netze aus.
   6. Klicken Sie mit der rechten Maustaste auf die Schaltfläche Berechnen.
3. Stellen Sie den Orientierungswinkel und das Eingangssignal ein und führen Sie eine zeitabhängige Studie durch.
   1. Klicken Sie im Modellgeneratorunter Globale Definitionenmit der linken Maustaste auf Parameter, und ändern Sie den Parameter Theta in den für die Simulation gewünschten Faserorientierungswinkel.
   2. Klicken Sie im Modellgenerator mitder linken Maustaste auf den Stammknoten des Modells, und wählen Sie Studie hinzufügen aus, um die Registerkarte Studie hinzufügen zu öffnen. Wählen Sie Zeitabhängige Studie, klicken Sie mit der linken Maustaste auf die Schaltfläche Studie hinzufügen und bearbeiten Sie die Registerkarte Einstellungen wie folgt.
      1. Stellen Sie die Zeiten auf "Bereich(0, (2*pi/omega)/39,2*pi/omega)" ein.
      2. Erweitern Sie Physik und Variablenauswahl; Lassen Sie nur das Kontrollkästchen Simulationskomponente "Lösen für" aktiviert.
      3. Erweitern Sie netzauswahl,und wählen Sie ein Netz für die Simulationskomponente aus. Ändern Sie die Netze der anderen Komponenten in Kein Netz.
      4. Erweitern Sie Studienerweiterungen, und aktivieren Sie das Kontrollkästchen Adaptive Netzverfeinerung. Wählen Sie die Geometrie der Simulationskomponente aus der Dropdown-Liste aus.
   3. Definieren Sie zeitabhängige Randbedingung.
      1. Klicken Sie unter dem aktuellen Komponentenknoten mit der rechten Maustaste auf Definitionen, und wählen Sie unter Funktionen die Option Wellenformaus.
      2. Ändern Sie auf der Registerkarte Einstellungen den Funktionsnamen in "Eingabe".
      3. Erweitern Sie Parameter, setzen Sie Typ auf Sinus, Winkelfrequenz auf "Omega", Amplitude auf V0.
      4. Wählen Sie für die Simulationskomponente unter dem Knoten Elektrische Ströme die Option Klemme aus und ändern Sie die Spannung in "Eingang(t[1/s])".
   4. Klicken Sie mit der rechten Maustaste auf die Schaltfläche Berechnen.

3. Analyse

1. Ladungsdichte
   1. Klicken Sie im Modellgenerator mit der rechten Maustaste auf den Knoten Ergebnisse, wählen Sie 3D-Plotgruppe aus, und bearbeiten Sie Einstellungen.
      1. Ändern Sie die Bezeichnung in "Ladungsdichte".
      2. Erweitern Sie Daten, und wählen Sie das parametrische Studiendataset in der Dropdown-Liste Datensatz aus.
      3. Erweitern Sie Farblegende und aktivieren Sie "Legenden anzeigen" und "Maximal- und Minimalwerte anzeigen".
   2. Klicken Sie im Modell-Generator unter dem Knoten Ergebnisse mit der rechten Maustaste auf Ladungsdichte, und wählen Sie Volumenaus. Fahren Sie mit der Registerkarte Einstellungen bearbeiten fort.
      1. Erweitern Sie Daten und wählen Sie "Vom übergeordneten Element" aus der Dropdown-Liste Datensatz.
      2. Erweitern Sie Ausdruck, und geben Sie "ec.rhoq" im Feld Ausdruck ein.
      3. Erweitern Sie Bereich und aktivieren Sie das Kontrollkästchen Manueller Farbbereich.
         1. Legen Sie minimum auf "-0.03" und maximum auf "0.03" fest.
      4. Erweitern Sie Farbgebung und Stil, legen Sie Farbgebung auf Farbtabelle, Farbtabelle auf Welle fest, aktivieren Sie Farblegende, aktivieren Sie Symmetrize Farbbereich.
      5. Klicken Sie im Modellgenerator mit der rechten Maustaste auf Volumen, und wählen Sie Filteraus.
         1. Geben Sie auf der Registerkarte Einstellungen "abs(ec.rhoq)>0.012" in den logischen Ausdruck für die Aufnahme ein.
   3. Klicken Sie mit der linken Maustaste auf die Schaltfläche Plot, um die Ergebnisse im Arbeitsfenster zu visualisieren.
2. Stromdichte
   1. Klicken Sie im Modellgenerator mit der rechten Maustaste auf den Knoten Ergebnisse, wählen Sie 3D-Plotgruppe aus, und bearbeiten Sie die Registerkarte Einstellungen.
      1. Ändern Sie die Bezeichnung in "Stromdichte".
      2. Erweitern Sie Daten, und wählen Sie das parametrische Studiendataset in der Dropdown-Liste Datensatz aus.
      3. Erweitern Sie Color Legend, aktivieren Sie "Legenden anzeigen" und "Maximale und minimale Werte anzeigen".
   2. Klicken Sie im Modell-Generator unter dem Knoten Ergebnisse auf Aktuelle Dichte, und wählen Sie Pfeilvolumenaus. Fahren Sie mit der Registerkarte Einstellungen bearbeiten fort.
      1. Erweitern Sie Daten und wählen Sie "Vom übergeordneten Element" aus der Dropdown-Liste Datensatz.
      2. Erweitern Sie Ausdruck und füllen Sie "ec. Jx", "ec. Jy", "ec. Jz" in den Ausdrucksfeldern für die Komponenten x, y und z.
      3. Erweitern Sie Pfeilpositionierung, und geben Sie 20 für alle Koordinaten Anzahl der Punkte ein.
      4. Erweitern Sie Farbgebung und Stil,legen Sie die Pfeillänge auf Normalisiert, die Pfeilbasis auf Mitte fest, aktivieren Sie den Skalierungsfaktor und legen Sie ihn auf 85 fest.
      5. Klicken Sie im Modell-Generator mit der rechten Maustaste auf Pfeilvolumen, und wählen Sie Farbausdruckaus.
         1. Geben Sie auf der Registerkarte Einstellungen im Feld Ausdruck die Datei "ec.normJ" ein.
         2. Erweitern Sie Farbgebung und Stil,legen Sie die Farbtabelle auf Datenverkehr fest, aktivieren Sie Farblegende und umgekehrte Farbtabelle.
   3. Klicken Sie auf die Schaltfläche Plot, um die Ergebnisse im Arbeitsfenster zu visualisieren.

Ergebnisse

Das vorgeschlagene Modell beschreibt Merkmale einer Verbundmatte mit parallelen Fasern, die in eine leitfähige Substanz eingetaucht und einem extern erzeugten elektrischen Potentialgradienten ausgesetzt ist. Simulationen zeigen, dass die Berücksichtigung der verschiedenen Komponenten eines Gerüsts auf Mikroskala wichtig ist und untersuchen, wie eine Änderung des Ausrichtungswinkels (Eingangssignal) der Fasern zum EF Variabilität in der Strom- und Ladungsdichte (Ausgangssignale) in der Nähe der Fasern erzeugen kann.

Es werden fünf verschiedene geometrische Komplexitätsstufen vorgestellt, die sich jeweils auf das Simulationsergebnis auswirken: glatte leitfähige Bramme (SC), glatte Platte mit nichtleitenden eingebetteten Fasern (SNC), rauer leitfähiger Verbundwerkstoff (RC), rauer Verbundwerkstoff mit nichtleitenden eingebetteten Fasern (RNC), rauer Verbundwerkstoff mit nichtleitenden eingebetteten Fasern und zwei Arten von periodischer Beschichtung (RNCd) (Abbildung 3). Abschnitt 1.5 des Protokolls enthält die Schritte zum Importieren der Geometrien in ein Projekt und Abschnitt 1.6 zeigt, wie diese Schritt für Schritt erstellt werden. Die ersten beiden Modelle berücksichtigen nicht die Oberflächenmorphologie. SC und RC berücksichtigen nicht die dielektrischen Eigenschaften des Faserkerns. Das RNC ist das vorgeschlagene Modell für nanofaserigen künstlichen Gerüste, während RNCd das vorgeschlagene Modell für ein ECM-Segment ist.

Die Minimierung der Rechenkosten wurde erreicht, indem die ES-Gerätegeometrie auf ein Volumen der Modelleinheit reduziert wurde, das die Mikroumgebung darstellt. Während die Breite und Länge eines ES-Geräts und eines Gerüsts leicht in der Größenordnung von einigen Zentimetern liegen kann, ist der Durchmesser der enthaltenden Fasern in der Regel niedriger als ein Mikrometer. Hier verwenden wir ein Gerüst, das mit dem Faserdurchmesser vergleichbar ist, um die durch das Seitenverhältnis induzierten Rechenkosten zu reduzieren und die Auswirkungen der faserigen Natur des Gerüsts auf die elektrische Mikroumgebung hervorzuheben. Der Rest des ES-Geräts wird durch elektrische Potentialrandbedingungen ersetzt, die so gewählt werden, dass eine grobe Annäherung an die Größe des elektrischen Feldes 100 V / m beträgt, ein häufig berichteter Stimulationsparameter. Darüber hinaus wird angenommen, dass ein Einheitsvolumen mit fünf parallelen Fasern - wie es in Simulationen verwendet wird, in Abbildung 3 dargestellt - repräsentativ für eine ganze planare Fasermatte ist. Drei Arten von Fasern können in einem 1D-Array unterschieden werden: innen zentral (mit der Längssymmetrieebene des Gerüsts, die sie in zwei Hälften teilt), innere Transitorium (mit seitlicher Oberfläche, die von anderen Fasern umgeben ist, aber mit asymmetrischen Seiten) und außen (am Rand des Gerüsts). Fünf ist die Mindestanzahl von Fasern, die erforderlich sind, um alle drei definierten Typen einzubeziehen.

Die Größe des Modellnetzelements erfordert besondere Aufmerksamkeit, da sie sich auf die Simulationsergebnisse auswirken und somit wichtige Effekte nicht aufdecken kann (Abbildung 4). Dies ist eine allgemeine Regel der Finite-Elemente-Methode und eine Implikation des Nyquist-Shannon-Abtastungssatzes. Je schneller die wesentlichen Simulationssignale im Raum schwanken, desto kleiner müssen die Netzelemente sein, um eine loyale Darstellung des Phänomens zu erzeugen. Andererseits: Je kleiner das Element, desto größer die Gesamtzahl der Modellbausteine und die Rechenkosten. Die in Abschnitt 2.1 eingerichtete adaptive Netzverfeinerung ist eine gute und einfache Methode, um diese gegensätzlichen Ziele auszugleichen, indem die Elementgröße nur dann verringert wird, wenn und solange dieser Vorgang zu einer signifikanten Änderung führt.

Ein zu einfaches Modell kann wichtige Effekte nicht darstellen(Abbildung 5, 6). Simulationen zeigen, dass die Berücksichtigung der Oberflächenmorphologie und der elektrischen Eigenschaften der Gerüstkomponente bei der Vorhersage elektrischer Mikroumgebungen nicht redundant ist. Während die Oberflächenmorphologie einen direkten Einfluss auf den stationären EF hat (vergleichen Sie SC und SNC mit RC, RNC und RNCd), zeigt ein Vergleich zwischen RC- und RNC-Vorhersagen, dass nichtleitende Faserkerne diesen Effekt verstärken. Aus Sicht der Modellierung zellulärer elektrischer Mikroumgebungen auf nanofaserigen Gerüsten sind die SC-, SNC- und RC-Modelle somit suboptimal. Es ist jedoch eine gute Praxis, die Komplexität schrittweise zu erhöhen, da Vergleiche zwischen den verschiedenen Phasen dazu beitragen, aufzuzeigen, welche Merkmale zu bestimmten Effekten führen.

Die Modellkomplexität wirkt sich auf die Änderung der Strom- und Ladungsdichte mit der Faserausrichtung auf den EF aus. Das vorgeschlagene Protokoll hilft, den Effekt hervorzuheben (Abbildung 5,6). Während das SC-Modell keine Variation der vorgeschlagenen Metriken zeigt, wenn seine Ausrichtung auf den elektrischen Potentialgradienten geändert wird, sagen die RNC-Modellsimulationen einen starken Kontrast zwischen der Matteneinheit mit Fasern, die auf den EF ausgerichtet sind, und der mit Fasern senkrecht voraus (Abbildung 7). Wenn die nichtleitenden Kerne dem Stromfluss im Weg stehen, bilden sie periodische Dämme, die zu abwechselnden Regionen mit hoher und niedriger Ladungsdichte führen.

Dynamische ES-Regime können mit zeitabhängigen Studien simuliert werden. Videos in ergänzenden Dateien zeigen Vorhersagen für eine sinusförmige Eingangsspannung auf einem vollständigen künstlichen Gerüstmodell (RNC), mit Fasern parallel oder senkrecht zum elektrischen Potentialgradienten. Kleine Ströme entlang der Fasern senkrecht zum EF treten auf, wenn die Ladung vom Gerüst freigesetzt wird, wenn die EF-Größe abnimmt. Dies zeigt, dass eine Stimulation nicht nur auftreten kann, während der externe EF vorhanden ist, sondern auch direkt nach dem Trennen - Siehe ergänzende Dateien für Videos.

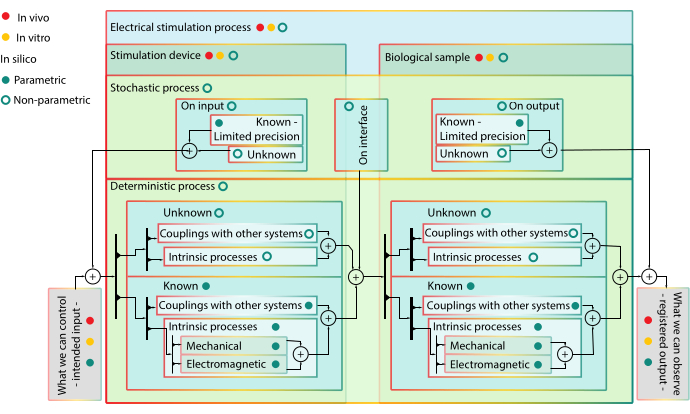
Abbildung 1: Hierarchisches Blockdiagramm der Modellierung - Vorteile und Grenzen der Modellierung mit In-vivo- und In-silico-Modellen. Blockfarbe markiert Blöcke auf derselben hierarchischen Ebene. Niedrigere Rangblöcke sind in höherrangigen Blöcken enthalten. Blockstrich-Farbmarkierungen Möglichkeit, den Block in eine bestimmte Art von Modell einzubeziehen - Kopplung mit anderen Systemblöcken haben kein Gelb in ihrem Strich, da sie keine Komponenten für In-vitro-Modelle sind. Kugeln wirken wie Ventile und bedeuten die Steuerbarkeit des Blocks. Wenn ein Ventil eingeschaltet ist, kann das Signal alle Pfeilpfade in den untergeordneten Subsystemen durchlaufen, die die Farbe des Ventils in ihrem Hub haben. Interpretation des Diagramms: Der ES-Prozess besteht aus dem Stimulationsgerät und dem biologischen Ziel, jeweils mit mehreren miteinander verbundenen deterministischen oder stochastischen Subprozessen, die nicht in vivo oder in vitro getrennt werden können, daher haben sie keine rote oder gelbe Klappe. Stochastische Prozesse greifen auch an der Schnittstelle zwischen Simulationsgerät und biologischer Probe ein, wenn beide stimuliert werden. Ein In-vitro-Modell entkoppelt das interessierende System (d.h. das Hautsegment) vom Rest des Organismus. So können nur intrinsische Prozesse des interessierenden Systems beobachtet werden, die von stochastischen Prozessen unterschiedlicher Art gekrönt werden. Die verschiedenen intrinsischen Prozesse können jedoch nicht separat stimuliert und identifiziert werden. Die In-silico-Modelle sind parametrisch für bekannte Komponenten - ihr Verhalten wird voraussichtlich eine bestimmte Form haben - und nicht parametrisch für das Unbekannte - da es keinen mechanistischen Grund gibt, einer bestimmten Extrapolation Glauben zu schenken. Alle in silico Komponenten können einzeln oder in verschiedenen Kombinationen simuliert werden, was die Darstellung verschiedener Hypothesen ermöglicht. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

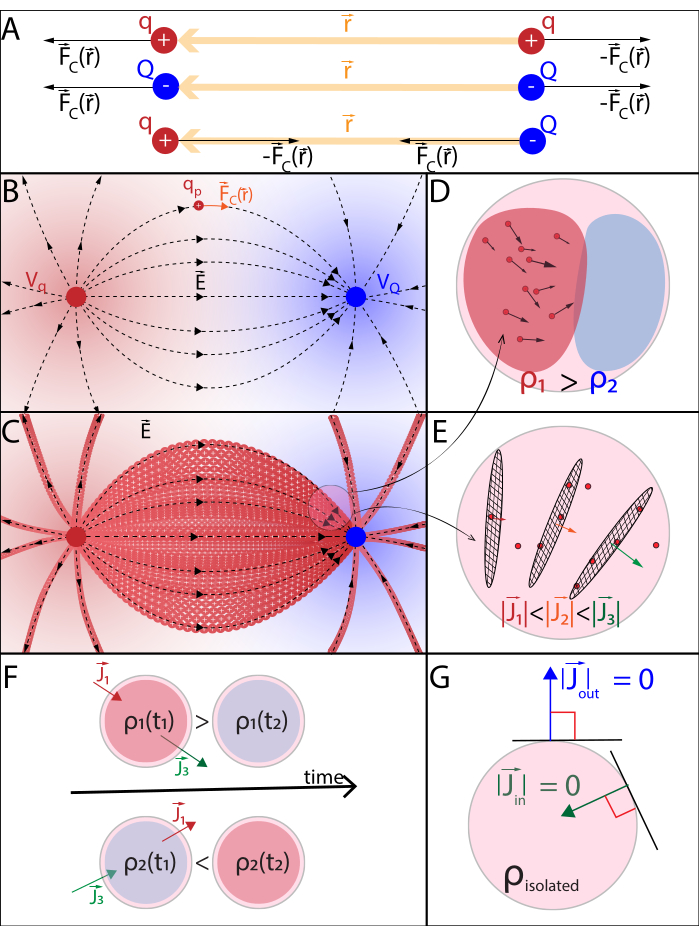
Abbildung 2: (A) Coulombsches Gesetz (B) Elektrisches Potentialfeld und mobile Sondenladung (C) Elektrischer Strom (D) Ladungsdichte (E) Stromdichte (F) Kontinuitätsgleichung (G) Ladungserhaltungsgesetz. (A) Elektrisch geladene stationäre Teilchen q und Q interagieren elektrostatisch durch Coulombs 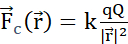Kraft. (B1) Jedes geladene Teilchen Q erzeugt an allen Positionen im Raum ein skalares Feld, das als elektrisches Potential bezeichnet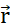 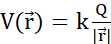wird: . Die maximale Arbeit, die erforderlich ist, um ein anderes geladenes Teilchen q von seiner Position zu 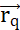bewegen, ist das Produkt zwischen der Ladung q und dem elektrischen Potential, das von Q an der Position erzeugt 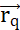wird. Das elektrische Potentialfeld, das von mehreren Teilchen erzeugt wird, ist die Summe der Felder, die von jedem einzelnen Teilchen erzeugt werden. (B2) Ein stationäres Feld mit festen Generatorteilchen q und Q, wirkt mit einem 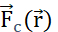auf ein Sondenteilchen mit positiver Ladung q_p. Als Reaktion darauf bewegt sich q_p, um das elektrische Potenzial seiner Position zu minimieren. Um die Bewegung von q_pzu beschreiben, kann man 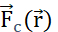aus dem 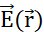elektrischen Potentialfeld das elektrische Feld ableiten: 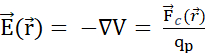. (C) Mehrere mobile positiv geladene Sondenteilchen, die gleichmäßig in einem stationären elektrischen Feld freigesetzt werden, folgen einer organisierten Bewegung. Um die Ladungskonfiguration zu verfolgen, ohne jedes Teilchen zu verfolgen, kann man zu jedem Zeitpunkt angeben: (D) wie der Raum von Teilchen besetzt ist, 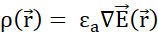indem jedem infinitesimalen Volumen gemäß dem Gaußschen Gesetz eine Ladungsdichte zugewiesen wird, und (E) wie Teilchen die Grenzflächen zwischen benachbarten infinitesimalen Volumina passieren, wobei jeder Grenze eine Stromdichte 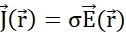gemäß dem Ohmschen Gesetz zugewiesen wird. (F) Ladung und Stromdichte entwickeln sich entsprechend der Kontinuitätsgleichung co-abhängig, da eine ungleichmäßige Partikelverschiebung entweder zur Akkumulation oder zum Verlust von Partikeln in einem bestimmten Volumen führt. (G) Innerhalb eines isolierten Systems herrscht das Ladungserhaltungsgesetz vor und es gibt keinen Zu- oder Abfluss geladener Teilchen. Verwendete Notationen:- q,Q,q_p Ladung und Name des geladenen Teilchens; 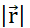- Euklidische Norm des Positionsvektors; k - Coulomb-Konstante; 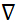- Gradientenoperator, ε_a - absolute Permittivität des Mediums; σ - Leitfähigkeit des Mediums. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

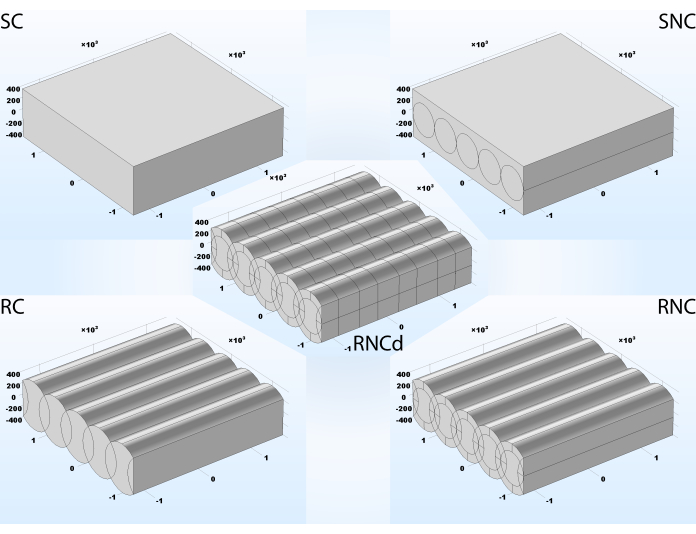
Abbildung 3: Fünf verschiedene Komplexitätsstufen für eine Fasermatte. SC- glatt mit leitfähigen eingebetteten Fasern, das einfachste Modell, ohne Berücksichtigung der Oberflächenmorphologie oder der unterschiedlichen Eigenschaften der Bestandteile; SNC- glatt mit nicht leitenden eingebetteten Fasern; RC- rau mit leitfähigen eingebetteten Fasern, die die Oberflächenmorphologie berücksichtigen, aber nicht die unterschiedlichen Komponenteneigenschaften; RNC- rau mit nicht leitenden eingebetteten Fasern, vollständiges vorgeschlagenes Modell von nanofaserigen künstlichen Gerüsten; RNCd- rau mit nicht leitenden eingebetteten Fasern, die mit zwei verschiedenen Materialien beschichtet sind, vollständiges vorgeschlagenes Modell für eine Schicht Kollagenfasern. Verwendete Längeneinheit: Nanometer. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

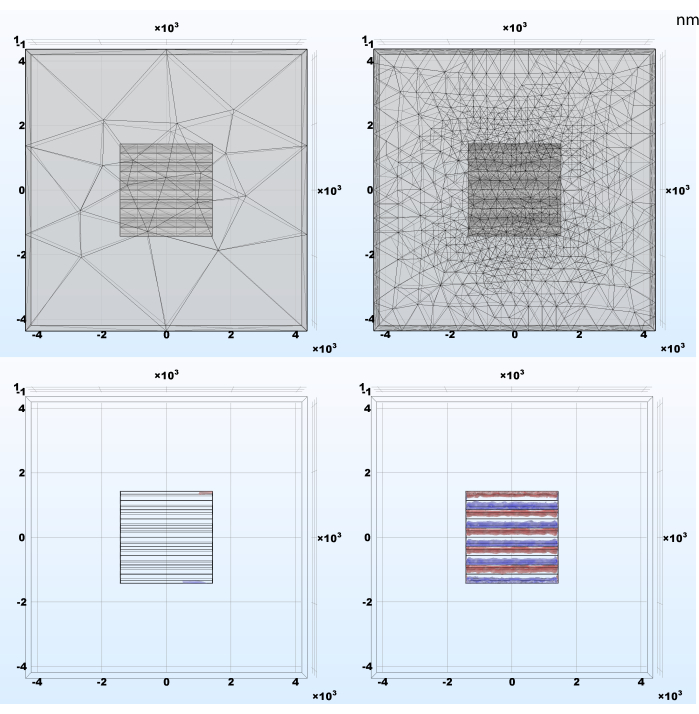
Abbildung 4: Beispielergebnisse der adaptiven Netzverfeinerung und der daraus resultierenden Ladungsdichte nach der Simulation. (Links) Automatisch erzeugtes Netz mit extra groben tetraedrischen Elementen; (Rechts) Anfängliches Netz adaptiv verfeinert während der stationären Studie; Kleinere Elemente sind für ein genaues Ergebnis in den Bereichen erforderlich, in denen simulierte Signale abrupte räumliche Veränderungen aufweisen. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

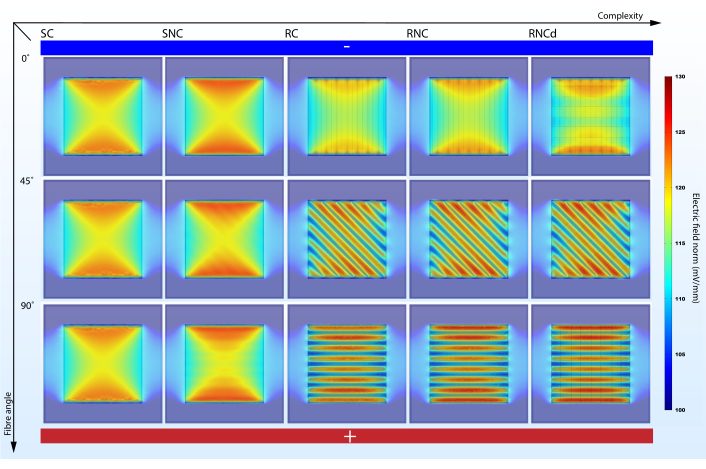
Abbildung 5:Der Faserausrichtungswinkel zum elektrischen Potentialgradienten beeinflusst die EF-Stärke in umgebenden Zellkulturmedien, wenn genügend Komplexität berücksichtigt wird. SC, SNC, RC, RNC und RNCd sind die verschiedenen Komplexitätsstufen für das in Abbildung 3dargestellte Fasermattenmodell. Die vertikale Achse markiert den Ausrichtungswinkel der Fasern zum elektrischen Potentialgradienten. Abstrakte Elektroden vorgestellt - Unterseite mit hohem elektrischem Potential und Oberseite mit niedrigem elektrischem Potential. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

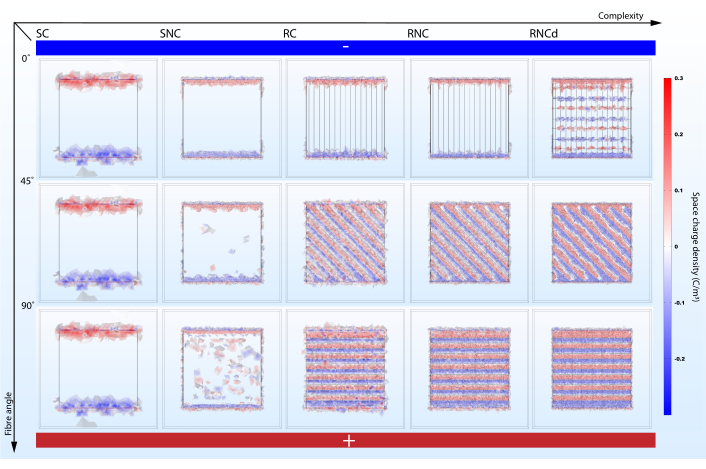
Abbildung 6:Der Faserausrichtungswinkel zum elektrischen Potentialgradienten beeinflusst die Raumladungsdichte in umgebenden Zellkulturmedien, wenn genügend Komplexität berücksichtigt wird. SC, SNC, RC, RNC und RNCd sind die verschiedenen Komplexitätsstufen für das in Abbildung 3dargestellte Fasermattenmodell. Die vertikale Achse markiert den Ausrichtungswinkel der Fasern zum elektrischen Potentialgradienten. Abstrakte Elektroden vorgestellt-Unterseite mit hohem elektrischem Potential und Oberseite mit niedrigem elektrischem Potential. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Abbildung 7: Die Ladungsbewegung wird durch die Ausrichtung der Gerüstfasern relativ zum EF beeinflusst. Beide Panels veranschaulichen Steady State RNC-Modellvorhersagen. Auf der linken Seite sind die Fasern parallel zum EF, während sie auf der rechten Seite senkrecht stehen. Das hellrote bis blaue Farbvolumen kennzeichnet die Ladungsdichte, während das Pfeilvolumen die aktuelle Dichteorientierung kennzeichnet. Die Farbe der Pfeile entspricht der aktuellen Dichtenorm. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Name	Ausdruck	Beschreibung
Ws	10 * Rc * med_ratio	Gerüstbreite
Ls	10 * Rc * med_ratio	Gerüstlänge
Hs	2 * Rf	Gerüsthöhe
med_ratio	1.5	Verhältnis von Zellkulturmedien zu Gerüst
Rc	278,5[nm]	Faserkernradius
r	1.5	Verhältnis von Faserkern zu Schicht
Rf	Rc*r	Faser mit Fellradius
Theta	90[Deg]	Faserorientierungswinkel
Lf	1,3*(Ls*cos(theta)+Ws*sin(theta))	Faserlänge
Tes	1	Verhältnis von Faserkernradius zu Abstand zwischen Fasern
n_1	2*(fix((Ws/(2*cos(theta))-Rf)/(2*tes*Rc))+3)*(cos(theta)!=0)+1*(cos(theta)==0)	Maximale Anzahl von Fasern, wenn Theta<=45
n_2	2*(fix((Ls/(2*sin(theta))-Rf)/(2*tes*Rc))+3)*(sin(theta)!=0)+1*(sin(theta)==0)	Maximale Anzahl von Fasern bei Theta>45
Überschuss	1,2 + 0,3 * abs (Sünde (2 * Theta))	Erster relativer Faserversatz vom Gerüst
D	Lf/5	Periodizität des Deckschichts
Stütze	0.46	Länge der ersten Schicht relativ zur Periodizität D
E	100[mV/mm]	Größe des elektrischen Feldes
V0	E*Ls*med_ratio	Klemmenspannung
Omega	500[Hz]	Zeitabhängige Untersuchung Spannungsfrequenz
p_sigma	0.5	Relative Leitfähigkeit der zweiten Beschichtung
p_eps	1.5	Zweite relative Dielektrizitätskonstante der Beschichtung

Tabelle 1: Für die Simulation verwendete Parameter

	Kultur Medien	PEDOT: PSS 1	PEDOT: PSS 2	Kollagen Hydratisiert 1	Kollagen Hydratisiert 2	Seidenfibroin	Kollagen Trocken
Elektrische Leitfähigkeit (S/m)	1.7014	1.00E-01	p_sigma * 0,1	2.00E-05	p_sigma * 2e-5	1.00E-08	2.50E-08
Relative Permittivität	80.1	2.2	p_eps * 2,2	9.89	p_eps * 9,89	7,81E+00	4.97

Tabelle 2: In der Simulation verwendete Materialeigenschaften

Ergänzende Dateien. Bitte klicken Sie hier, um diese Datei herunterzuladen.

Diskussion

Das vorgeschlagene Protokoll schlägt eine einheitliche Modellierungslösung für natürliche und künstliche Gerüste vor und unterstreicht die Notwendigkeit, die Nanostruktur von faserigen Gerüsten zu berücksichtigen, wenn die Auswirkungen von EF auf Zellen untersucht werden, die auf solche Materialien gesät werden. Obwohl eine grobe Annäherung an die EF-Intensität (Elektrodenpotentialdifferenz dividiert durch den Abstand zwischen den Elektroden) eine Feldstärke von 100 mV/mm erwarten würde, sagen Simulationen stationäre Feldstärken in verschiedenen Bereichen der Matte bis zu 30% höher voraus (Abbildung 5). Dieses Ergebnis sollte für das Design und die Dateninterpretation von ES-Experimenten von Interesse sein, da der Zelltod durch zu starke EFs verursacht werden kann. Die Freizulegende elektrische Mikroumgebung würde eine direkte Korrelation zwischen ES und zellulärer Entwicklung ermöglichen. Während mehrere Studien eine detaillierte morphologische Analyse der verwendeten Gerüste^33,43,59präsentieren, untersuchen sie nicht das Zusammenspiel zwischen der Struktur, den elektrischen Eigenschaften der Materialien und dem EF. Dieses Protokoll kann diese Verbindung ermöglichen, da Parameter wie Faserradius, Schichtdicke, Abstand zwischen Fasern und elektrische Eigenschaften der Komponentenmaterialien entsprechend jedem Experiment geändert werden können, indem die globalen Definitionen in den Schritten 1.2 und 1.3 geändert werden. Daher können kundenspezifische 3D-Ortsauflöserladungs- und Stromdichtevorhersagen sowohl für statische als auch für dynamische ES-Regime erstellt werden.

Die Optimierung des Gerüstdesigns kann durch die RNC- und RNCd-Modelle mit weiten Parameterbereichsuntersuchungen angestrebt werden, wobei die vorgeschlagenen Morphologien oder Teile davon skaliert werden. Alternativ können andere Gerüstkonfigurationen mit dem vorgeschlagenen Protokoll untersucht werden, indem die Array-Typen in Abschnitt 1.6.5 von linear auf dreidimensional geändert und in Abschnitt 1.6.2 die Gerüstgeometrie angepasst wird. Die Gerüstoptimierung kann jedoch nicht ohne ein Ziel durchgeführt werden. Während für Tissue Engineering-Zwecke das Zellschicksal im Vordergrund steht, ist ein klareres Bild darüber, welche Reize seine Hauptdeterminanten sind, unerlässlich, wenn eine zuverlässige Kontrolle gewünscht wird. Ladungs- und Stromdichte sind gute Deskriptoren zellulärer elektrischer Mikroumgebungen, da sie das Zusammenspiel zwischen dem EF und den elektrischen Eigenschaften der verschiedenen Komponentenmaterialien komplexer Gerüste wie ECM zeigen. Das Protokoll zeigt, wie Vorhersagen für diese Metriken bei einer nanofibrous Gerüstgeometrie berechnet werden können, und hebt die Bedeutung des Ausrichtungswinkels der Fasern mit dem EF hervor. Vorhersagen von Ladung und Stromdichte könnten dann mit der Zellentwicklung verknüpft und so Gerüst- und ES-Regime für bestimmte Aufgaben optimiert werden.

Interessanterweise zeigt eine Studie, dass die EF-Exposition bei Verbundfolien mit Nanofasern senkrecht zum externen EF im Vergleich zu Filmen mit paralleler Ausrichtung 60 eine mechanische Spannung erzeugte, die mehr als doppelt so stark war wie^{die Festigkeit.} Die berichtete mechanische Spannung könnte ein Ergebnis von Coulomb-Kräften sein, die zwischen geladenen Fasern wirken, vorhergesagt durch die groben Modellsimulationen (RC, RNC, RNCd) (Abbildung 6). Während diese Simulationen bei der Untersuchung dieser Hypothese nützlich sein könnten, muss beachtet werden, dass die berichteten experimentellen Ergebnisse in einem System mit kapazitiver Kopplung erhalten wurden und die Simulation eine direkte Kopplung darstellt.

Ein limitierender Faktor für zukünftige mögliche Verwendungen des Protokolls zur Schätzung eines zellulären Eingangssignals ist die Parameterunsicherheit. Geometrisch unsichere Parameter sind die Schichtdicke und der Abstand zwischen den Faserkernen. Die erste könnte abgeleitet werden, indem der Wert gefunden wird, der zu einer Massenimpedanz führt, die experimentell validiert werden kann. Der zweite kann aus hochauflösenden Materialscans extrahiert werden. Parameter, die die physikalischen Eigenschaften der Materialien beschreiben, werden ebenfalls von Unsicherheiten beeinflusst. Die elektrische Leitfähigkeit und Dielektrizitätskonstante von beispielhaften Materialien unterscheiden sich jedoch weit mehr als die experimentelle Messgenauigkeit (Tabelle 2). Daher würden die berichteten Effekte trotz moderater Messfehler beibehalten.

Die Ergebnisse zeigen, wie bei zu wenig Modellkomplexität relevante Informationen versteckt werden können. Es ist wichtig anzuerkennen, dass das Protokoll eine vereinfachte Version des physikalischen Phänomens simuliert, da es die unterschiedliche Art der am Prozess beteiligten Materialien - Leiter (Elektroden), Halbleiter (Beschichtung), Dielektrikum (Faserkerne) und Elektrolyt (umgebende Substanz) - nicht berücksichtigt, die den Ladungstransport beeinflussen können. Dieses Problem kann in zukünftigen Modellerweiterungen berücksichtigt werden, indem Energieübertragungsverzögerungen an den Grenzflächen (d. H. Faradische Reaktionen) und Ionentransportverzögerungen innerhalb des Elektrolyten hinzugefügt werden. Das Hinzufügen von Komplexität sollte jedoch durch experimentelle Validierung geleitet werden, da ein einfaches Modell, das das meiste von dem, was beobachtet wird, reproduziert, nützlicher ist als ein bemerkenswert genaues Modell, das wenig mehr Informationen hinzufügt, aber sehr empfindlich auf die Unsicherheit vieler konstituierender Parameter reagiert.

Da das Endziel des Tissue Engineering darin besteht, Bioreaktoren zu entwickeln, die nicht nur einen oder zwei Aspekte von In-vivo-Umgebungen nachahmen, sondern alle zellulären Entwicklungshinweise replizieren und kontrollieren^61,müssen elektromagnetische und mechanische In-silico-Modelle sowie Modelle der Wärmeübertragung zwischen Bioreaktorkomponenten kombiniert werden. In einer anschließenden Modellierungsphase können auch Kopplungsphänomene zwischen diesen Wechselwirkungen wie ohmsche Erwärmung, elektrolytische Flüssigkeitsströmung, morphologische Gerüstverformungen als Reaktion auf elektrische Stimulation⁶⁰ und Piezoelektrizität⁶² hinzugefügt werden. Modelle sollten jedoch erst zusammengeführt werden, nachdem jedes Modell experimentell validiert wurde. Auf diese Weise können wir den Einfluss jeder Komponente in der zellulären Mikroumgebung besser verstehen und wie Reize optimiert werden können.

Wenn das vorgeschlagene Modell experimentell validiert ist, kann es mit Modellen biologischer Zellen kombiniert werden - Abbildung 1. Ladungsdichtemuster und Modulationen könnten die Aktivität bestimmter Ionenpumpen asymmetrisch beeinflussen, die Bindung an die Faser von Proteinen beeinflussen, die die Membranadhäsion⁶³ antreiben und somit Migration, Proliferationsmuster und Morphogenese steuern⁶⁴. Die Erforschung dieser Hypothesen ist der Weg nach vorn, um die Mechanismen zu verstehen, die den Reaktionen von Gewebe und Zellen auf ES zugrunde liegen.

Materialien

Name	Company	Catalog Number	Comments
Comsol multiphysics 5.2 AC/DC module	COMSOL	-	FEM modelling software