Modélisation par éléments finis d’un microenvironnement électrique cellulaire

Résumé

Cet article présente une stratégie pour construire des modèles par éléments finis de matériaux conducteurs fibreux exposés à un champ électrique (FE). Les modèles peuvent être utilisés pour estimer l’apport électrique que reçoivent les cellules ensemencées dans ces matériaux et évaluer l’impact de la modification des propriétés, de la structure ou de l’orientation des matériaux constitutifs de l’échafaudage.

Résumé

Des études cliniques montrent que la stimulation électrique (SE) est une thérapie potentielle pour la guérison et la régénération de divers tissus. Comprendre les mécanismes de réponse cellulaire lorsqu’ils sont exposés à des champs électriques peut donc guider l’optimisation des applications cliniques. Les expériences in vitro visent à aider à les découvrir, offrant l’avantage de plages d’entrées et de sorties plus larges qui peuvent être évaluées de manière éthique et efficace. Cependant, les progrès des expériences in vitro sont difficiles à reproduire directement en milieu clinique. Principalement, c’est parce que les dispositifs ES utilisés in vitro diffèrent considérablement de ceux adaptés à une utilisation par le patient, et le chemin des électrodes aux cellules ciblées est différent. Traduire les résultats in vitro en procédures in vivo n’est donc pas simple. Nous soulignons que la structure et les propriétés physiques du microenvironnement cellulaire jouent un rôle déterminant dans les conditions réelles des essais expérimentaux et suggérons que les mesures de la distribution de charge peuvent être utilisées pour combler le fossé entre in vitro et in vivo. Compte tenu de cela, nous montrons comment la modélisation in silico par éléments finis (FEM) peut être utilisée pour décrire le microenvironnement cellulaire et les changements générés par l’exposition au champ électrique (FE). Nous soulignons comment l’EF se couple avec une structure géométrique pour déterminer la distribution de charge. Nous montrons ensuite l’impact des entrées dépendantes du temps sur le mouvement de la charge. Enfin, nous démontrons la pertinence de notre nouvelle méthodologie de modèle in silico à l’aide de deux études de cas : (i) des échafaudages fibreux in vitro de Poly(3,4-éthylènedioxythiophène) poly(styrènesulfonate) (PEDOT-PSS) et (ii) du collagène in vivo dans la matrice extracellulaire (ECM).

Introduction

ES est l’utilisation des CE dans le but de contrôler les cellules et les tissus biologiques. Son mécanisme est basé sur le stimulus physique transduit à la cellule lorsque les biomolécules à l’intérieur et autour d’elle sont exposées à un gradient de tension généré de l’extérieur. Les particules chargées sont engagées dans un mouvement organisé régi par la loi de Coulomb, générant des forces de traînée sur les particules non chargées. L’écoulement du fluide et la distribution de charge qui en résultent modifient les activités et les fonctions cellulaires telles que l’adhésion, la contraction, la migration, l’orientation, la différenciation et la prolifération¹ alors que la cellule tente de s’adapter au changement des conditions microenvironnementales.

Comme les FE sont contrôlables, non invasifs, non pharmacologiques et qu’il a été démontré qu’ils ont un impact efficace sur le comportement cellulaire essentiel, l’ES est un outil précieux pour l’ingénierie tissulaire et la médecine régénérative. Il a été utilisé avec succès pour guider le développement neuronal^2,squelettique^3,musculaire cardiaque^4,os⁵ et peau^6. De plus, comme il améliore l’ionophorèse^7,il est utilisé comme traitement alternatif ou complémentaire aux traitements pharmacologiques conventionnels. Son efficacité dans la gestion de la douleur est encore débattue car des essais cliniques de meilleure qualité sont attendus^8,9,10. Néanmoins, aucun effet indésirable n’a été rapporté et il a le potentiel d’améliorer le bien-être des patients^11,12^,13,14,15.

Alors que seuls les essais cliniques peuvent donner un verdict définitif sur l’efficacité d’une procédure, des modèles in vitro et in silico sont nécessaires pour éclairer la conception d’un traitement prévisible contre les SE, car ils offrent un contrôle plus fort sur un plus large éventail de conditions expérimentales. Les utilisations cliniques étudiées de l’ES sont la régénération osseuse^16,17, la récupération des muscles dénervés^18,19, la régénération axonale après la chirurgie^20,21, le soulagement de la douleur²², la cicatrisation des^{plaies 23,24,25} et l’administration de médicaments iontophorétiques²⁶. Pour que les dispositifs ES soient largement introduits sur toutes les applications cibles possibles, les essais cliniques n’ont pas encore établi de preuves plus solides pour un traitement efficace. Même dans les domaines où les études in vivo sur les animaux et les humains rapportent systématiquement des résultats positifs, le grand nombre de méthodes rapportées, associé à trop peu de conseils sur la façon de choisir entre elles et à un prix d’acquisition élevé, dissuade les cliniciens d’investir dans des dispositifs ES²⁷. Pour pallier cela, le tissu cible ne peut plus être traité comme une boîte noire (limite d’expériences in vivo) mais doit être vu comme une synergie complexe de plusieurs sous-systèmes(Figure 1).

De multiples expériences ES ont été réalisées in vitro au cours des années^{28,29,30,31,32,33,34}. La plupart d’entre eux ne caractérisent l’ES que par la chute de tension entre les électrodes divisée par la distance entre elles - une approximation approximative de l’amplitude du champ électrique. Cependant, le champ électrique lui-même n’influence que les particules chargées, pas directement les cellules. En outre, lorsque plusieurs matériaux sont interposés entre le dispositif et les cellules, l’approximation approximative peut ne pas tenir.

Une meilleure caractérisation du signal d’entrée nécessite une vision claire de la façon dont le stimulus est transduit à la cellule. Les principales méthodes d’octroi d’ES sont le couplage direct, capacitif et inductif^35,36. Les dispositifs pour chaque méthode diffèrent par le type d’électrode (tige, planaire ou enroulement) et le placement par rapport au tissu cible (en contact ou isolé)³⁵. Les dispositifs utilisés in vivo pour des traitements plus longs doivent être portables, de sorte que les électrodes et la plupart du temps la source d’énergie sont implantées ou attachées à la peau sous forme de pansements ou de patchs électroactifs. Le gradient de tension généré déplace les particules chargées dans la zone de traitement.

Comme elle a un impact sur le flux de particules chargées qui en résulte à proximité des cellules, la structure de l’échafaudage est de la plus haute importance dans la conception des protocoles ES. Différentes configurations de transport de charge se produisent si le matériau de la plate-forme, la technique de synthèse, la structure ou l’orientation par rapport au gradient de tension changent. In vivo, la disponibilité et le mouvement des particules chargées sont influencés non seulement par les cellules, mais aussi par le réseau de collagène et le liquide interstitiel composant l’ECM de soutien. Les échafaudages d’ingénierie sont de plus en plus utilisés pour mieux recréer les microenvironnements cellulaires naturels in vitro^1,35. Parallèlement, l’ECM est un échafaudage naturel complexe.

Les échafaudages artificiels sont à base de métaux, de polymères conducteurs et de carbone, conçus en mettant l’accent sur l’équilibrage de la biocompatibilité avec les performances électrochimiques et la stabilité à long terme³⁶. Un type d’échafaudage polyvalent est le tapis fibreux électrofilé qui offre une topographie contrôlable à l’échelle nanométrique. Cela peut être conçu pour ressembler à l’ECM, fournissant ainsi des signaux mécaniques similaires qui aident à la régénération d’un large éventail de tissus³⁷. Pour avoir un impact significatif sur les SE, les tapis doivent être conducteurs dans une certaine mesure. Cependant, les polymères conducteurs sont difficiles à électrospiner et le mélange avec des supports isolants limite la conductivité des fibres résultantes³⁸. Une solution consiste à polymériser un monomère conducteur à la surface d’une fibre diélectrique, ce qui donne une bonne résistance mécanique et des propriétés électriques du produit final³⁸. Un exemple est le revêtement de fibres électro filées de soie avec le PEDOT-PSS³⁹semi-conducteur . La combinaison de signaux mécaniques et électromagnétiques accélère considérablement la croissance des neurites^40,41,42. Les neurites suivent l’alignement des fibres des échafaudages, et s’allongent plus après exposition à un EF parallèle aux fibres qu’à un EF vertical⁴³. De même, l’alignement des échafaudages fibreux sur l’EF favorise également la maturation myogénique³³.

L’ECM est principalement composé de protéines fibreuses^{formant 44,}dont le collagène de type I étant le constituant majeur dans tous les tissus animaux à l’exception du cartilage (riche en collagène de type II)^44. Le tropocologène (TC), triple conformation hélicoïdale des brins polypeptidiques, est le motif structurel des fibrilles de collagène⁴⁵. Les images de microscopie électronique à transmission et de microscopie à force atomique de fibrilles de collagène montrent un motif à bandes D-périodique⁴⁶ expliqué par le modèle Hodge & Petruska⁴⁷ comme des réseaux réguliers de lacunes et de chevauchements TC⁴⁵. Les tendons sont composés d’une matrice fiillaire collagène alignée protégée par une matrice protéoglycane hautement hydrophile non collagène^48,49. La décorine est un petit protéoglycane riche en leucine (SLRP) capable de lier les régions d’espace des fibrilles de collagène et de se connecter à d’autres SLRP par leurs chaînes latérales de glycosaminoglycanes (GAG)⁴⁹. Les études réalisées sur les tendons montrent que leurs propriétés électriques changent de manière significative lorsqu’ils sont hydratés^50,51,mécanisme de transport de charge passant de protonique à ionique à mesure que le niveau d’hydratation augmente^51. Cela suggère que la conduction électrique le long d’une fibrilles de collagène de type I pourrait être rendue possible par une couche décorine-eau, avec des régions d’espace et de chevauchement ayant des conductivités électriques et des constantes diélectriques différentes.

Comme la reconstitution identique de l’ECM par des échafaudages artificiels est improbable, les connaissances produisant une synergie entre in vivo et in vitro rendue possible par des résultats traduisibles semblent être dans une impasse. La modélisation in silico permet non seulement la traduction entre les deux, mais ajoute également des avantages importants dans la caractérisation des processus inconnus impliqués dans ES. La comparaison des observations in vivo avec les observations in vitro peut apporter des informations sur la force de couplage entre le tissu cible et le reste de l’organisme, mais ne révèle pas les limites actuelles des connaissances. L’inconnu peut être exposé en observant la différence entre ce qui devrait se produire en fonction des connaissances actuelles et ce qui se passe. Les expériences in silico basées sur la modélisation mathématique permettent de diviser le processus en sous-processus connus et inconnus. De cette façon, des phénomènes non pris en compte dans le modèle sont révélés lorsque les prédictions in silico sont comparées à des expériences in vitro et in vivo.

La formation et la mise à l’essai d’hypothèses concernant le ou les mécanismes sous-jacents de la façon dont les cellules et les tissus sont affectés par les champs électriques sont entravées par le grand nombre de paramètres⁵² qui doivent être testés séparément. Pour définir des conditions expérimentales représentatives, le processus ES doit être divisé en sous-processus(Figure 1)et les signaux d’entrée dominants affectant le comportement des cellules doivent être identifiés. Les modèles représentant les effets physiques fondamentaux de l’ES sur les cellules décrivent le domaine qui couple l’EF avec la cellule - celui des particules chargées⁵³. Le comportement des particules à l’extérieur de la cellule dépend du microenvironnement et peut être étudié séparément de la cellule. Le signal d’entrée dominant pour la cellule est le sous-ensemble de sorties de dispositif ES qui provoque le plus grand degré de variabilité dans la réponse de la cellule. Le plus petit sous-ensemble des paramètres expérimentaux complets qui peuvent générer des variations dans tous les signaux d’entrée de cellule dominante peut être utilisé pour diminuer la dimension de l’espace des paramètres et le nombre de cas de test.

L’entrée du modèle cible biologique ES doit être un sous-ensemble des signaux de sortie produits par le dispositif ES qui sont utiles pour décrire les effets physiques des ES sur les cellules. Un bioréacteur simple avec couplage direct a la même structure que les cellules électrochimiques électrolytiques. Les modèles de ceux-ci montrent la distribution de densité de courant primaire (tenant compte de la résistance à la solution), secondaire (tenant également compte des réactions faradiques) ou tertiaire (tenant également compte de la diffusion ionique). Comme la complexité se traduit par un coût de calcul, le modèle le plus simple convient le mieux aux explorations spatiales de paramètres. Les simulations de composites fibreux motivées par les propriétés des matériaux⁵⁴ se concentrent sur les propriétés des matériaux en vrac résultant d’une micro-architecture complexe, et ne peuvent donc pas décrire les effets locaux de l’exposition à l’EF. Les modèles in silico existants, motivés par l’ES, se concentrent sur l’échantillon biologique, qu’il s’agisse d’une seule cellule immergée dans un milieu homogène^55,56,57,ou de tissus complexes à espace extracellulaire homogène^58. La densité de charge et de courant(Figure 2)peut servir de signaux d’interface entre les modèles du dispositif ES et l’échantillon biologique, ou entre différents composants du dispositif ES. Le protocole FEM proposé utilise les équations décrites à la figure 2 et a été utilisé pour étudier comment les paramètres dépendants de l’échafaudage peuvent être utilisés pour moduler ces deux signaux, indépendamment de l’EF généré par une configuration de couplage direct. Les résultats soulignent qu’il est nécessaire de tenir compte des propriétés électriques de l’échafaudage ou de l’ECM lors de l’étude de l’impact de l’ES sur les cellules cibles.

Protocole

1. Construire le modèle dans COMSOL

1. Ouvrez COMSOL et sélectionnez Modèle vide.
2. Paramètres : Dans Model Builder, cliquez avec le bouton droit sur Définitions globales, sélectionnez Paramètreset ajoutez des paramètres conformément au Tableau 1.
3. Matériaux : Ajoutez des matériaux ayant des propriétés conformément au tableau 2.
   1. Dans le Générateur de modèles, sous Définitions globales, cliquez avec le bouton droit sur Matériau et sélectionnez Matériau vierge.
   2. Ajouter des propriétés de matériau : dans les paramètres du matériau nouvellement ajouté, développez Propriétés du matériau > Propriétés de base, sélectionnez Permittivité relative et appuyez sur le symbole '+' pour ajouter une propriété. Répétez l’étape pour Conductivité électrique.
   3. Dans le contenu du matériau, remplissez les propriétés actuelles du matériau conformément au tableau 2.
4. Définition du composant : dans l’onglet Accueil du ruban supérieur, cliquez avec le bouton gauche sur Ajouter un composant et sélectionnez 3D. Un nouveau nœud de composant apparaîtra dans le Générateur de modèles.
5. Géométrie : Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, cliquez avec le bouton gauche sur Insérer, double-cliquez sur le modèle complet et sélectionnez la séquence appropriée (SC/SNC/RC/RNC/RNCd).
6. Vous pouvez également créer la géométrie à partir de zéro en suivant les étapes subordonnées.
   1. Dans le Générateur de modèles, cliquez avec le bouton gauche sur Géométrie sous le nœud de composant actuel. Le même nœud Géométrie sera référencé dans les étapes subordonnées suivantes. Dans la fenêtre Paramètres, remplacez l’unité Longueur par nm et assurez-vous que l’option « Mettre à l’échelle les valeurs lors du changement d’unité » n’est pas cochée.
   2. Géométrie de l’échafaudage
      1. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie et sélectionnez Bloc.
      2. Dans l’onglet Paramètres, remplissez l’étiquette « Étendues d’échafaudage ».
      3. Développez Taille et forme et remplissez « Ws », « Ls », « Hs » pour Largeur, Profondeur et Hauteur.
      4. Développez Position et remplacez la base par Centre.
      5. Développez Sélections d’entités résultantes, sélectionnez Nouveau et ajoutez « Sélection d’échafaudage ».
   3. Étendues de la substance environnante : dans le Générateur de modèles, sous Géométrie, cliquez avec le bouton droit sur Étendues de l’échafaudage et sélectionnez Dupliquer, puis modifiez l’onglet Paramètres.
      1. Remplacez l’étiquette par « Étendues de média ».
      2. À chaque case de la section Taille et Shape, ajoutez « med_ratio * » avant le paramètre existant.
      3. Dans les sélections d’entités résultantes, ajoutez une nouvelle sélection en tant que « Sélection de média ».
   4. Géométrie d’une fibre (SC passer à 1.6.6)
      1. Noyau (RC passer à 1.6.4.2)
         1. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, sélectionnez Cylindreet modifiez l’onglet Paramètres comme suit.
         2. Remplacez l’étiquette par « Core ».
         3. Développez Taille et forme et remplissez « Rc » et « Lf » pour Rayon et Hauteur.
         4. Développez Position et remplissez « -excess*Ws/2 » et « -Lf/2 » pour x et y.
         5. Développez Axe et remplacez le type d’axe par axe des y.
         6. Développez Sélections d’entités résultantes et ajoutez « Sélection principale ».
      2. Manteau (SNC passer à 1.6.5)
         1. Dalle (RC ou RNC passer à 1.6.4.2.2; RNCd passer à 1.6.4.2.3)
            1. Dans le Générateur de modèles, sous Géométrie, cliquez avec le bouton droit sur Étendues de l’échafaudage et sélectionnez Dupliquer. Assurez-vous que le duplicata (extensions d’échafaudage 1) vient juste après Core dans la séquence géométrique.
            2. Dans l’onglet Paramètres, remplacez l’étiquette par « Manteau ».
            3. Dans l’onglet Paramètres, développez Sélections des entités résultantes et créez « Sélection de fibre ».
            4. Passez à la section 1.6.5.
         2. Homogène
            1. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, sélectionnez Cylindre et modifiez son onglet Paramètres comme suit.
            2. Remplacez l’étiquette par « Manteau ».
            3. Développez Taille et forme et remplissez « Rf » et « Lf » pour Rayon et Hauteur.
            4. Développez Position et remplissez « -excess*Ws/2 » et « -Lf/2 » pour x et y.
            5. Développez Axe et remplacez le type d’axe par l’axe y (passage RC à 1.6.4.2.2.7).
            6. Développez Calques, remplissez « Rf-Rc » pour Épaisseur et ne laissez que « Calques sur le côté » coché.
            7. Développez Sélections d’entités résultantes et ajoutez " Sélection de couche " ou, pour RC, « Sélection de fibre » (RC passer à 1.6.5).
            8. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie et sélectionnez Supprimer les entités.
            9. Dans l’onglet Paramètres, remplacez Le niveau d’entrée géométrique par Domaine et choisissez Sélection de couche pour la sélection.
            10. Supprimez tous les domaines sauf le domaine 3 de la zone de sélection (le cœur du cylindre en couches).
            11. Développez Sélections d’entités résultantes et sélectionnez Sélection de couche.
            12. Passez à la section 1.6.5.
         3. Tableau périodique de deux types
            1. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie et sélectionnez Cylindre. Cliquez avec le bouton droit sur l’élément nouvellement créé et sélectionnez Dupliquer. Modifiez leur onglet Paramètres comme suit.
               1. Réglez l’étiquette sur « Manteau 1 » / « Manteau 2 ».
               2. Définissez le rayon sur Rf.
               3. Réglez la hauteur sur « D*prop"/"D*(1-prop) ».
               4. Développez la position et remplissez « -excess*Ws/2 » pour x et « -Lf/2"/ »-Lf/2+D*prop » sur y.
               5. Développez Axe et remplacez le type d’axe par axe y.
               6. Développez la section Calques et remplissez « Rf-Rc »; Assurez-vous que seule la case « Calques sur le côté » est cochée.
               7. Développez Sélections des entités résultantes et créez « Sélection de couche 1"/ « Sélection de couche 2 ».
            2. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie et sélectionnez Supprimer les entités.
               1. Dans l’onglet Paramètres, remplacez Niveau d’entrée géométrique par Domaine et sélectionnez cylindre 2 (cyl2) et cylindre 3 (cyl3) dans la fenêtre graphique.
               2. Supprimez tous les domaines sauf le domaine 3 de la zone de sélection (le cœur des cylindres en couches).
               3. Développez Sélections d’entités résultantes et créez Sélection de couche.
            3. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, développez Transformations et sélectionnez Tableau. Modifier l’onglet Paramètres comme suit.
               1. Sélectionnez « Coat Selection » pour les objets d’entrée.
               2. Définissez Type de tableau sur Linéaire.
               3. Réglez Taille sur « Lf/D ».
               4. Réglez Déplacement sur l’axe y sur « D ».
   5. Géométrie d’un réseau de fibres orientées
      1. Core Array (RC passer à la version 1.6.5.2)
         1. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, développez Transformations et sélectionnez Faire pivoter.
            1. Dans l’onglet Paramètres, activez le commutateur Objets d’entrée et sélectionnez Sélection du noyau dans la liste déroulante. Assurez-vous que la case Conserver les objets d’entrée n’est pas cochée.
            2. Développez Angle de rotation et remplissez « thêta » pour Rotation.
            3. Développez Sélections d’entités résultantes et créez " Sélection de fibre « Sélection de fibre ».
         2. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, développez Transformations et sélectionnez Tableau.
            1. Changez l’étiquette en « Core Array ».
            2. Sélectionnez Sélection principale dans la liste déroulante des objets Input.
            3. Développez Taille, remplacez le type de tableau par Linéaire et remplissez « n_1*(thêta<=45) +n_2*(thêta>45) » pour Taille.
            4. Développez Déplacement et remplissez « 2*tes*Rc*cos(theta) », « 2*tes*Rc*sin(theta) » pour x et y.
            5. Développez Sélections d’entités résultantes et sélectionnez « Sélection de fibre ».
      2. Coat Array (SNC passe à la 1.6.5.3)
         1. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, développez Transformations et sélectionnez Faire pivoter.
            1. Dans l’onglet Paramètres, activez le commutateur Objets d’entrée et sélectionnez Sélection de couche dans la liste déroulante. Assurez-vous que l’case « Conserver les objets d’entrée » n’est pas cochée.
            2. Développez Angle de rotation et remplissez « thêta » pour Rotation.
            3. Développez Sélections d’entités résultantes et sélectionnez « Sélection de fibre ».
         2. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, développez Transformations et sélectionnez Tableau.
            1. Remplacez l’étiquette par « Coat Array ».
            2. Sélectionnez Sélection de couche dans la liste déroulante des objets d’entrée.
            3. Développez Taille, remplacez le type de tableau par Linéaire et remplissez « n_1*(thêta<=45) +n_2*(thêta>45) » pour Taille.
            4. Développez Déplacement et remplissez « 2*tes*Rc*cos(theta) », « 2*tes*Rc*sin(theta) » pour x et y.
            5. Développez Sélections d’entités résultantes et sélectionnez « Sélection de fibre ».
      3. Échafaudage coupé
         1. Unir les fibres : dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, développez Booléens et partitions et sélectionnez Union.
            1. Changez l’étiquette en « Fibres ».
            2. Activez le commutateur Objets d’entrée et sélectionnez Sélection de fibre dans la liste déroulante.
            3. Assurez-vous que la case « Conserver les objets d’entrée » n’est pas cochée.
            4. Assurez-vous que l’option « Conserver les limites intérieures » est cochée.
            5. Développez Sélections d’entités résultantes et sélectionnez Sélection de l’échafaudage dans la liste déroulante.
         2. Effectuer une coupe : dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, développez Booléens et partitions et sélectionnez Intersection.
            1. Changez l’étiquette en « Échafaudage ».
            2. Activez le commutateur Objets d’entrée et sélectionnez Sélection de l’échafaudage dans la liste déroulante.
            3. Assurez-vous que la case « Conserver les objets d’entrée » n’est pas cochée.
            4. Assurez-vous que l’option « Conserver les limites intérieures » est cochée.
   6. Géométrie d’ensemble
      1. Définissez la géométrie de la substance environnante.
         1. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie, développez Booléens et partitions et sélectionnez Différence. Passez à l’onglet Paramètres.
         2. Dans la liste déroulante Objets à ajouter, sélectionnez Sélection du média.
         3. Dans la liste déroulante Objets à soustraire, sélectionnez Sélection de l’échafaudage.
         4. Assurez-vous que les cases « Conserver les objets d’entrée » et « Conserver les limites intérieures » sont toutes deux cochées.
      2. Supprimer la zone Extensions de média.
         1. Dans le Générateur de modèles, cliquez avec le bouton droit sur Géométrie et sélectionnez Supprimer les entités. Passez à l’onglet Paramètres.
         2. Sélectionnez Domaine dans la liste déroulante Niveau d’entrée géométrique.
         3. Sélectionnez Sélection de média dans la liste déroulante Sélection.
         4. Supprimez « dif1 » de la zone de sélection.
   7. Construire la géométrie
      1. Sous le nœud Géométrie, assurez-vous que le dernier élément avant le nœud Sélections cumulatives est Union de formulaire et non Assemblage de formulaire. Si nécessaire, cliquez avec le bouton droit sur Assemblage de formulaire et remplacez Action par « Former une union » dans l’onglet Paramètres.
      2. Dans le Générateur de modèles, cliquez avec le bouton gauche sur Géométrie et sélectionnez Tout générer.
7. Matériaux
   1. Dans le Générateur de modèles, sous le nœud Composant actuel, cliquez avec le bouton droit sur Matériaux et sélectionnez Lien de matériau.
   2. Répétez la section cinq fois pour autant de fois que de matériaux sont considérés en fonction du niveau de complexité.
   3. Associez les matériaux pour chaque composant dans l’ordre suivant : substance environnante, couches, noyaux.
   4. Dans l’onglet Paramètres, choisissez Media/Scaffold (pour SC, SNC, RC)/Coat/Core Selection dans la liste déroulante Sélection.
   5. Développez les paramètres de lien et choisissez le matériau approprié dans la liste déroulante.
8. Maillage
   1. Dans le Générateur de modèles, cliquez avec le bouton gauche sur le nœud Maillage sous le composant actif.
   2. Dans l’onglet Paramètres, sélectionnez Normal dans la liste déroulante Taille de l’élément et cliquez avec le bouton gauche sur Tout générer.
9. Physique : dans le Générateur de modèles, cliquez avec le bouton gauche sur le composant actuel, sélectionnez Ajouter une physique, développez le module AC/DC dans l’onglet Ajouter une physique, sélectionnez le module Courants électriques (ec) et cliquez sur Ajouter au composant.
   1. Conditions aux limites : dans l’onglet Graphiques, sélectionnez la vue xy.
      1. Sol : Dans le Model Builder,faites un clic droit sur le nœud Courants électriques et sélectionnez Sol.
      2. Assurez-vous que le commutateur de sélection de la sélection de frontière est actif et cliquez avec le bouton gauche de la souris sur la face de substance environnante la plus haute parallèle au plan xz pour ajouter la limite 5 dans la zone de sélection de frontière.
      3. Terminal : Dans le Model Builder,faites un clic droit sur le nœud Courants électriques et sélectionnez Terminal.
      4. Assurez-vous que le commutateur de sélection de la sélection de frontière est actif et cliquez avec le bouton gauche de la souris sur la face de substance environnante la plus basse parallèle au plan xz pour ajouter la frontière 2 dans la zone de sélection de frontière.
      5. Développez la section Terminal et sélectionnez Tension dans la liste déroulante Type de terminal ; remplissez V0 pour Tension.
   2. Ajoutez de la complexité si nécessaire : Enregistrez le composant actuel et revenez à l’étape 1.4 pour suivre un autre chemin de complexité (SC/SNC/RC/RNC/RNCd).

2. Effectuer une simulation

1. Raffinement adaptatif du maillage
   1. Dans Model Builder, cliquez avec le bouton gauche sur le nœud racine du modèle et sélectionnez Ajouter une étude pour ouvrir l’onglet Ajouter une étude, sélectionnez Étude stationnaire et cliquez avec le bouton droit sur le bouton Ajouter une étude.
   2. Créez une étape d’étude pour chaque composant créé : sous le nœud Étude, cliquez avec le bouton droit sur Étape 1 : Étude stationnaire et sélectionnez Dupliquer.
   3. Pour chaque étape de l’étude, modifiez l’onglet paramètres avec les détails du composant correspondant.
      1. Développer la sélection de la physique et des variables; dans la colonne Résoudre pour, ne laissez que le composant actif coché.
      2. Développez Extensions d’étude et cochez la case Affinement du maillage adaptatif.
      3. Sélectionnez la géométrie du composant actuel dans la liste déroulante en regard de Adaptation en géométrie.
   4. Dans Model Builder, cliquez avec le bouton droit sur Étude 1 et sélectionnez Calculer. Cela générera des maillages adaptés pour toutes les géométries des composants avec leur angle d’orientation actuel.
2. Définissez l’angle d’orientation et effectuez une étude stationnaire.
   1. Dans Model Builder, sous Définitions globales, cliquez avec le bouton gauche sur Paramètres et remplacez le paramètre thêta par l’angle d’orientation de la fibre souhaité pour la simulation.
   2. Pour chaque composant, dans le Générateur de modèles, développez le nœud du composant, cliquez avec le bouton droit sur Géométrie et sélectionnez Tout générer.
   3. Dans Model Builder, cliquez avec le bouton droit sur l’étude d’affinement du maillage adaptatif et sélectionnez calculer.
   4. Dans Model Builder, cliquez avec le bouton gauche sur le nœud racine du modèle et sélectionnez Ajouter une étude pour ouvrir l’onglet Ajouter une étude, sélectionnez Étude stationnaire et cliquez avec le bouton droit sur le bouton Ajouter une étude.
   5. Dans Model Builder, sous l’étude nouvellement ajoutée, cliquez avec le bouton gauche sur Étape 1, développez la sélection du maillage et, pour chaque composant, sélectionnez les maillages générés dans l’étude d’affinement du maillage adaptatif.
   6. Cliquez avec le bouton droit sur le bouton Calculer.
3. Définissez l’angle d’orientation, le signal d’entrée et effectuez une étude en fonction du temps.
   1. Dans Model Builder, sous Définitions globales, cliquez avec le bouton gauche sur Paramètres et remplacez le paramètre thêta par l’angle d’orientation de la fibre souhaité pour la simulation.
   2. Dans le Générateur de modèles, cliquez avec le bouton gauche sur le nœud racine du modèle et sélectionnez Ajouter une étude pour ouvrir l’onglet Ajouter une étude. Sélectionnez Étude dépendante du temps, cliquez avec le bouton gauche sur le bouton Ajouter une étude et modifiez l’onglet Paramètres comme suit.
      1. Réglez les heures sur « plage(0, (2 * pi / oméga) / 39,2 * pi / oméga) ».
      2. Développer la sélection de la physique et des variables; ne laissez que la case à cocher « Résoudre pour » du composant de simulation.
      3. Développez Sélection de maillage et sélectionnez un maillage pour le composant de simulation. Remplacez les maillages des autres composants par Aucun maillage.
      4. Développez Extensions d’étude et cochez la case affinement du maillage adaptatif ; sélectionnez la géométrie du composant de simulation dans la liste déroulante.
   3. Définissez une condition aux limites dépendante du temps.
      1. Sous le nœud de composant actuel, cliquez avec le bouton droit sur Définitions et, sous Fonctions, sélectionnez Forme d’onde.
      2. Dans l’onglet Paramètres, changez le nom de la fonction en « Entrée ».
      3. Développez Paramètres, définissez Typesur Sinus , Fréquence angulaire sur « oméga », Amplitude sur V0.
      4. Pour le composant de simulation, sous son nœud Courants électriques, sélectionnez Terminal et remplacez Tension par « Entrée(t[1/s]) ».
   4. Cliquez avec le bouton droit sur le bouton Calculer.

3. Analyse

1. Densité de charge
   1. Dans le nœud Résultats du Générateur de modèles, cliquez avec le bouton droit de la souris, sélectionnez Groupe de tracés 3D et modifiez Paramètres.
      1. Remplacez l’étiquette par « Densité de charge ».
      2. Développez Données et sélectionnez le jeu de données d’étude paramétrique dans la liste déroulante Ensemble de données.
      3. Développez Légende des couleurs et cochez « Afficher les légendes » et « Afficher les valeurs maximales et minimales ».
   2. Cliquez avec le bouton droit sur Densité de charge sous le nœud Résultats dans le Générateur de modèles et sélectionnez Volume; passez à l’onglet Paramètres.
      1. Développez Données et sélectionnez « À partir du parent » dans la liste déroulante Ensemble de données.
      2. Développez Expression et remplissez « ec.rhoq » dans la zone Expression.
      3. Développez Plage et cochez la case Plage de couleurs manuelle.
         1. Définissez le minimum sur « -0,03 » et le maximum sur « 0,03 ».
      4. Développez Coloration et style, définissez Coloriage sur Table de couleurs, Table de couleurs sur Vague, cochez la case Légende de couleur, cochez Symmetriser la plage de couleurs.
      5. Cliquez avec le bouton droit sur Volume dans Model Builder et sélectionnez Filtrer.
         1. Dans l’onglet Paramètres, remplissez « abs(ec.rhoq)>0.012 » dans l’expression logique à inclure.
   3. Cliquez avec le bouton gauche sur le bouton Tracer pour visualiser les résultats dans la fenêtre graphique.
2. Densité de courant
   1. Dans le Générateur de modèles, cliquez avec le bouton droit sur le nœud Résultats, sélectionnez Groupe de tracés 3D et modifiez l’onglet Paramètres.
      1. Remplacez l’étiquette par « Densité de courant ».
      2. Développez Données et sélectionnez le jeu de données d’étude paramétrique dans la liste déroulante Ensemble de données.
      3. Développez Légende descouleurs , cochez « Afficher les légendes » et « Afficher les valeurs maximales et minimales ».
   2. Cliquez avec le bouton droit sur Densité actuelle sous le nœud Résultats dans model Builder et sélectionnez Volume fléché; passez à l’onglet Paramètres.
      1. Développez Données et sélectionnez « À partir du parent » dans la liste déroulante Ensemble de données.
      2. Développez Expression et remplissez « ec. Jx », « ec. Jy », « ec. Jz » dans les zones Expression pour les composants x, y et z respectivement.
      3. Développez Positionnement de la flèche et remplissez 20 pour tous les nombres de coordonnées de points.
      4. Développez Coloration et style, définissez longueur de la flèche sur Normalisé, Base de flèche sur Centre, vérifiez facteur d’échelle et définissez-le sur 85.
      5. Cliquez avec le bouton droit sur Volume fléché dans Model Builder et sélectionnez Expression de couleur.
         1. Dans l’onglet Paramètres, remplissez « ec.normJ » dans la zone Expression.
         2. Développez Coloration et style, définissez la table des couleurs sur Trafic, cochez légende des couleurs et Inverser la table des couleurs.
   3. Cliquez sur le bouton Tracer pour visualiser les résultats dans la fenêtre graphique.

Résultats

Le modèle proposé décrit les caractéristiques d’un tapis composite avec des fibres parallèles, immergé dans une substance conductrice et exposé à un gradient de potentiel électrique généré de l’extérieur. Les simulations montrent que la prise en compte des différents composants d’un échafaudage est importante à l’échelle microscopique et explorent comment le changement d’angle d’alignement (signal d’entrée) des fibres par rapport à l’EF peut générer une variabilité de la densité de courant et de charge (signaux de sortie) à proximité des fibres.

Cinq étapes de complexité géométrique différentes sont présentées, chacune ayant un effet sur le résultat de la simulation : dalle conductrice lisse (SC), dalle lisse avec fibres incorporées non conductrices (SNC), composite conducteur brut (RC), composite brut avec fibres incorporées non conductrices (RNC), composite brut avec fibres incorporées non conductrices et deux types de revêtement périodique (RNCd)(Figure 3). La section 1.5 du protocole présente les étapes d’importation des géométries dans un projet et la section 1.6 montre comment les créer étape par étape. Les deux premiers modèles ne tient pas compte de la morphologie de surface. SC et RC ne sont pas responsables des propriétés diélectriques du noyau de la fibre. Le RNC est le modèle proposé pour les échafaudages artificiels nanofibreux, tandis que le RNCd est le modèle proposé pour un segment ECM.

La minimisation des coûts de calcul a été réalisée en réduisant la géométrie du dispositif ES à un volume unitaire modèle représentant le microenvironnement. Alors que la largeur et la longueur d’un appareil ES et d’un échafaudage peuvent facilement être de l’ordre de quelques centimètres, le diamètre des fibres contenant est généralement inférieur à un micron. Ici, nous utilisons une coupe d’échafaudage comparable au diamètre de la fibre pour réduire le coût de calcul induit par le rapport d’aspect et mettre en évidence l’effet de la nature fibreuse de l’échafaudage sur le microenvironnement électrique. Le reste du dispositif ES est remplacé par des conditions aux limites de potentiel électrique choisies de sorte qu’une approximation approximative de l’amplitude du champ électrique soit de 100 V / m, un paramètre de stimulation fréquemment rapporté. De plus, un volume unitaire avec cinq fibres parallèles - comme celui utilisé dans les simulations, présenté à la figure 3 - est supposé être représentatif d’un tapis fibreux planaire entier. Trois types de fibres peuvent être distingués dans un réseau 1D: intérieur central (avec le plan de symétrie longitudinal de l’échafaudage les divisant en deux), transitoire intérieur (avec une surface latérale entourée d’autres fibres mais avec des côtés asymétriques) et extérieur (au bord de l’échafaudage). Cinq est le nombre minimum de fibres requis pour inclure les trois types définis.

La taille de l’élément de maillage du modèle nécessite une attention particulière car elle peut avoir un impact sur les résultats de simulation et ne pas exposer les effets importants (Figure 4). Ceci est une règle générale de la méthode des éléments finis et une implication du théorème d’échantillonnage de Nyquist-Shannon. Plus les signaux de simulation essentiels fluctuent rapidement dans l’espace, plus les éléments maillés doivent être petits pour produire une représentation fidèle du phénomène. D’autre part, plus l’élément est petit, plus le nombre total de blocs de construction du modèle et le coût de calcul sont élevés. Le raffinement adaptatif du maillage mis en place à la section 2.1 est une méthode bonne et facile pour équilibrer ces objectifs opposés en diminuant la taille de l’élément uniquement lorsque et aussi longtemps que cette opération produit un changement significatif.

Un modèle trop simpliste peut échouer en présentant des effets importants(Figure 5,6). Les simulations montrent que la prise en compte de la morphologie de surface et des propriétés électriques des composants de l’échafaudage n’est pas redondante dans la prédiction des microenvironnements électriques. Alors que la morphologie de surface a un impact direct sur l’EF stationnaire (comparer SC et SNC avec RC, RNC et RNCd), une comparaison entre les prédictions RC et RNC montre que les noyaux de fibres non conductrices amplifient cet effet. Du point de vue de la modélisation des microenvironnements électriques cellulaires sur des échafaudages nanofibreux, les modèles SC, SNC et RC sont donc sous-optimaux. Cependant, il est de bonne pratique d’ajouter progressivement de la complexité, car les comparaisons entre les différentes étapes aident à indiquer quelles caractéristiques donnent lieu à des effets spécifiques.

La complexité du modèle a un impact sur le changement de densité de courant et de charge avec l’alignement de la fibre sur l’EF. Le protocole proposé permet de mettre en évidence l’effet (Figure 5,6). Alors que le modèle SC ne montre aucune variation dans les mesures proposées lorsque son alignement sur le gradient de potentiel électrique est modifié, les simulations du modèle RNC prédisent un contraste puissant entre l’unité de tapis avec des fibres alignées sur l’EF et celle avec des fibres perpendiculaires(Figure 7). Lorsque les noyaux non conducteurs se trouvent sur le chemin de l’écoulement du courant, ils forment des barrages périodiques qui conduisent à des régions alternées de densité de charge élevée et faible.

Les régimes ES dynamiques peuvent être simulés avec des études dépendantes du temps. Des vidéos dans des fichiers supplémentaires montrent des prédictions faites pour une tension d’entrée sinusoïdale sur un modèle d’échafaudage artificiel complet (RNC), avec des fibres parallèles ou perpendiculaires au gradient de potentiel électrique. De petits courants le long des fibres perpendiculaires à l’EF apparaissent lorsque la charge est libérée de l’échafaudage à mesure que la magnitude de l’EF diminue. Cela montre que la stimulation peut se produire non seulement lorsque l’EF externe est présent, mais aussi juste après sa déconnexion - Voir les fichiers supplémentaires pour les vidéos.

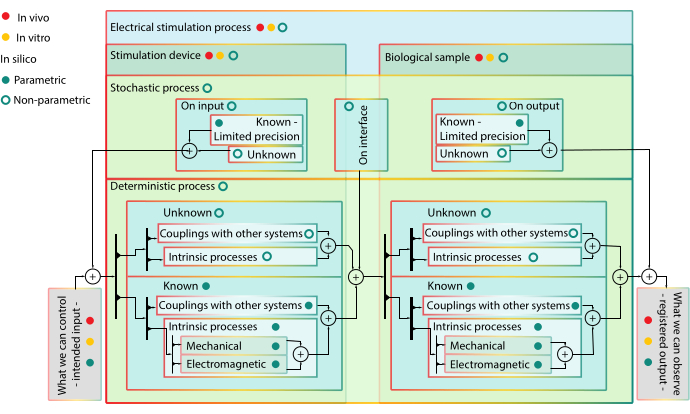
Figure 1: Schéma fonctionnel hiérarchique de la modélisation - avantages et limites de la modélisation avec des modèles in vivo et in silico. La couleur des blocs marque les blocs au même niveau hiérarchique. Les blocs de rang inférieur sont inclus dans ceux de rang supérieur. Les marques de couleur de trait de bloc peuvent inclure le bloc dans un certain type de modèle - le couplage avec d’autres blocs système n’a pas de jaune dans leur course, car ils ne sont pas des composants pour les modèles in vitro. Les balles agissent comme des vannes et signifient la contrôlabilité du bloc. Lorsqu’une vanne est activée, le signal peut traverser tous les chemins de flèche dans les sous-systèmes subordonnés qui ont la couleur de la vanne dans leur course. Interprétation du diagramme: le processus ES est composé du dispositif de stimulation et de la cible biologique, chacun avec plusieurs sous-processus déterministes ou stochastiques interconnectés qui ne peuvent pas être séparés in vivo ou in vitro, ils n’ont donc pas de valve rouge ou jaune. Les processus stochastiques interviennent également sur l’interface entre le dispositif de simulation et l’échantillon biologique lorsqu’ils sont tous deux stimulés. Un modèle in vitro découple le système d’intérêt (c.-à-d. le segment de peau) du reste de l’organisme. Ainsi, seuls des processus intrinsèques du système d’intérêt surmontés de processus stochastiques de nature différente peuvent être observés. Cependant, les différents processus intrinsèques impliqués ne peuvent pas être stimulés et identifiés séparément. Les modèles in silico sont paramétriques pour les composants connus - leur comportement devrait être d’une certaine forme - et non paramétriques pour l’inconnu - car il n’y a pas de raison mécaniste de donner du crédit à une certaine extrapolation. Tous les composants in silico peuvent être simulés séparément ou dans différentes combinaisons, ce qui permet de dépeindre différentes hypothèses. Veuillez cliquer ici pour voir une version agrandie de cette figure.

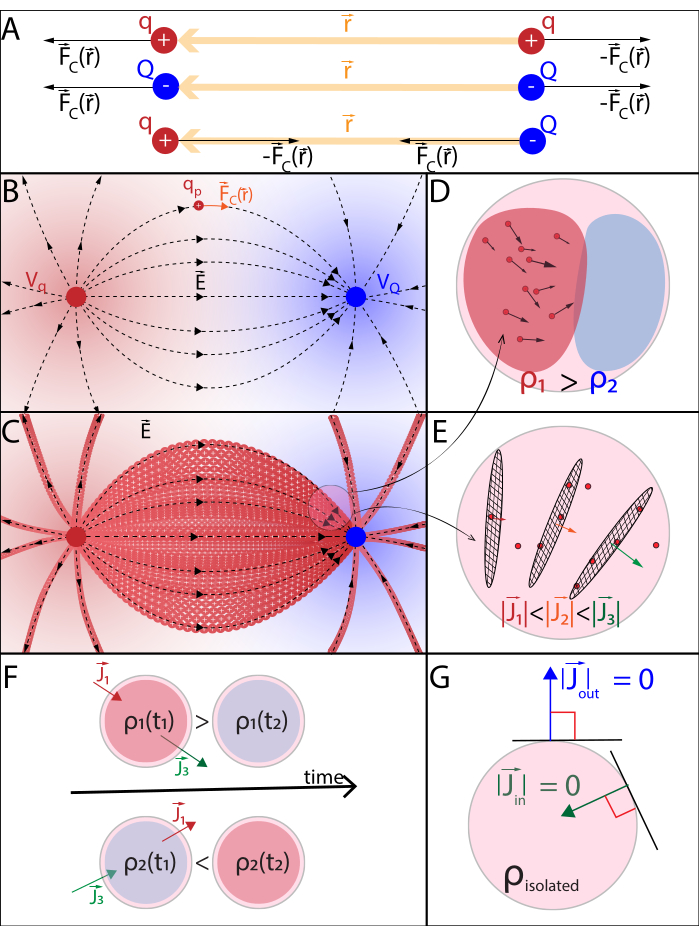
Figure 2: (A) Loi de Coulomb (B) Champ de potentiel électrique et charge de sonde mobile (C) Courant électrique (D) Densité de charge (E) Densité de courant (F) Équation de continuité (G) Loi de conservation de charge. (A) Les particules stationnaires chargées électriquement q et Q interagissent électrostatiquement par la force de 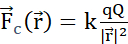Coulomb. (B1) Chaque particule chargée Q génère un champ scalaire appelé potentiel électrique à toutes les positions 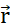dans l’espace : 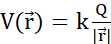. Le travail maximum requis pour déplacer une autre particule chargée q de sa position 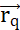est le produit entre la charge q et le potentiel électrique généré par Q à la position 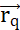. Le champ de potentiel électrique généré par plusieurs particules est la somme des champs générés par chaque particule individuelle. (B2) Un champ stationnaire avec des particules génératrices fixes q et Q, agit avec a 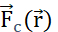sur une particule de sonde à charge positive q_p. En réponse, q_p se déplace pour minimiser le potentiel électrique de sa position. Pour décrire le mouvement de q_p, on peut dériver 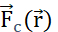et le champ électrique du champ de potentiel électrique 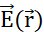: 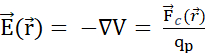. (C) Plusieurs particules mobiles chargées positivement sont libérées uniformément dans un champ électrique stationnaire suivent un mouvement organisé. Pour suivre la configuration de la charge sans suivre chaque particule, on peut spécifier à chaque instant: (D) comment l’espace est occupé par les particules, en attribuant une densité de charge 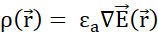à chaque volume infinitésimal, selon la loi de Gauss, et (E) comment les particules traversent les surfaces limites entre les volumes infinitésimaux voisins, attribuant une densité de courant 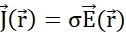à chaque frontière selon la loi d’Ohm. (F) La charge et la densité de courant évoluent de manière co-dépendante selon l’équation de continuité, car le déplacement non uniforme des particules entraîne une accumulation ou une perte de particules dans un certain volume. (G) Dans un système isolé, la loi de conservation de la charge prévaut et il n’y a pas d’entrée ou de sortie de particules chargées. Notations utilisées:- q,Q,q_p charge et nom de la particule chargée; 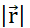- norme euclidienne du vecteur position ; k - constante de Coulomb ; 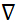- opérateur de gradient, ε_a - permittivité absolue du milieu; σ - conductivité du milieu. Veuillez cliquer ici pour voir une version agrandie de cette figure.

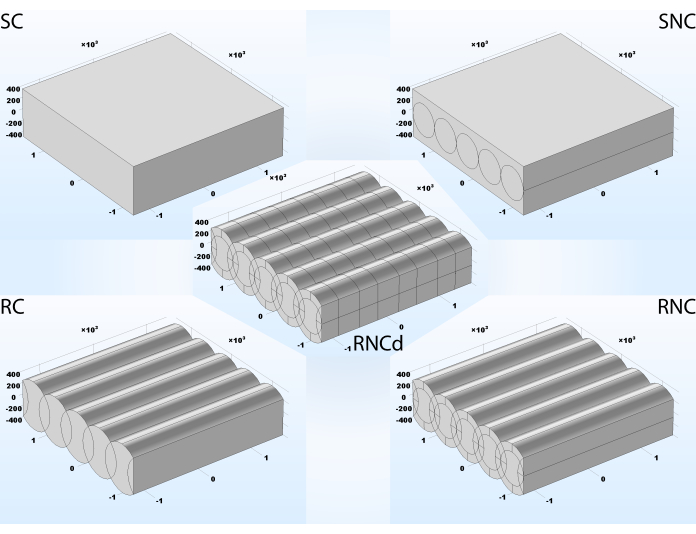
Figure 3: Cinq niveaux de complexité différents pour un tapis fibreux. SC- lisse avec des fibres conductrices incorporées, le modèle le plus simple, ne tenant pas compte de la morphologie de surface ou des propriétés différentes des composants constitutifs; SNC- lisse avec des fibres intégrées non conductrices; RC- rugueux avec des fibres conductrices incorporées, tenant compte de la morphologie de surface, mais pas des propriétés différentes des composants; RNC- rugueux avec des fibres incorporées non conductrices, modèle complet proposé d’échafaudages artificiels nanofibreux; RNCd- rugueux avec des fibres incorporées non conductrices recouvertes de deux matériaux différents, modèle complet proposé pour une feuille de fibres de collagène. Unité de longueur utilisée: nanomètres. Veuillez cliquer ici pour voir une version agrandie de cette figure.

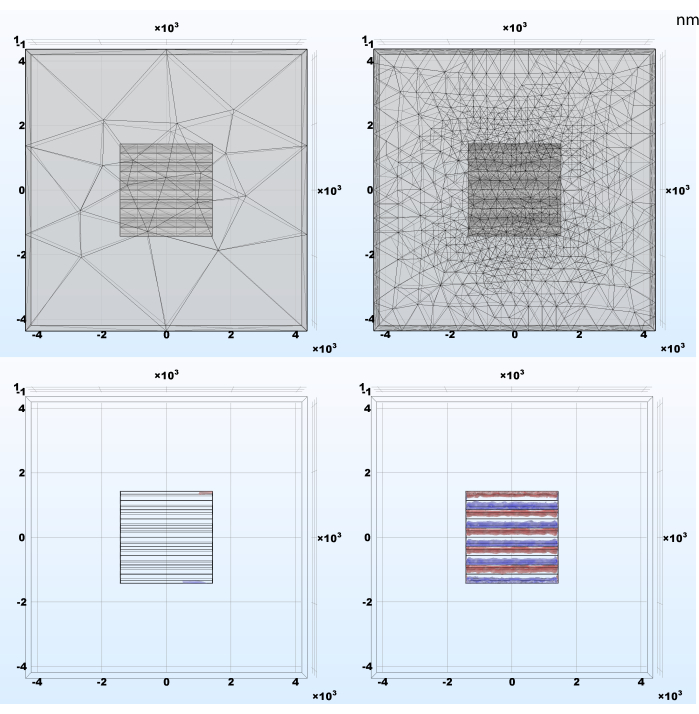
Figure 4: Exemples de résultats de l’affinement adaptatif du maillage et de la densité de charge résultante à la suite de la simulation. (À gauche) Maillage généré automatiquement avec des éléments tétraédriques extra grossiers; (À droite) Maillage initial affiné de manière adaptative pendant l’étude stationnaire; des éléments plus petits sont nécessaires pour obtenir un résultat précis dans les zones où les signaux simulés ont des changements spatiaux brusques. Veuillez cliquer ici pour voir une version agrandie de cette figure.

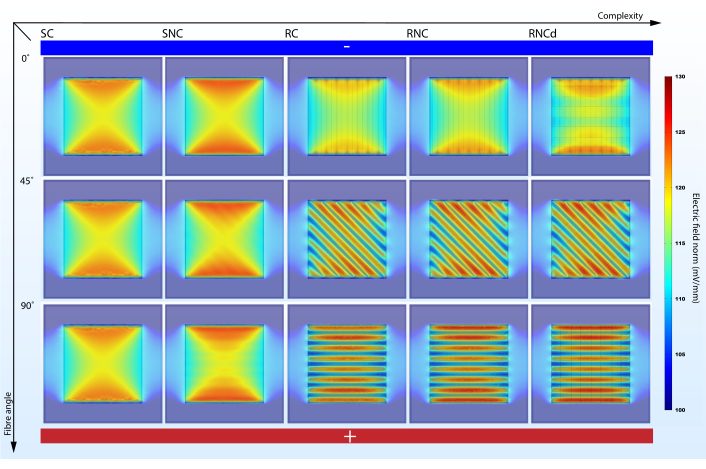
Figure 5: L’angle d’alignement de la fibre par rapport au gradient de potentiel électrique a un impact sur la force de l’EF dans les milieux de culture cellulaire environnants lorsque la complexité est suffisante. SC, SNC, RC, RNC et RNCd sont les différents niveaux de complexité pour le modèle de tapis fibreux présenté à la figure 3. L’axe vertical marque l’angle d’alignement des fibres par rapport au gradient de potentiel électrique. Électrodes abstraites présentées - côté inférieur à fort potentiel électrique et côté supérieur à faible potentiel électrique. Veuillez cliquer ici pour voir une version agrandie de cette figure.

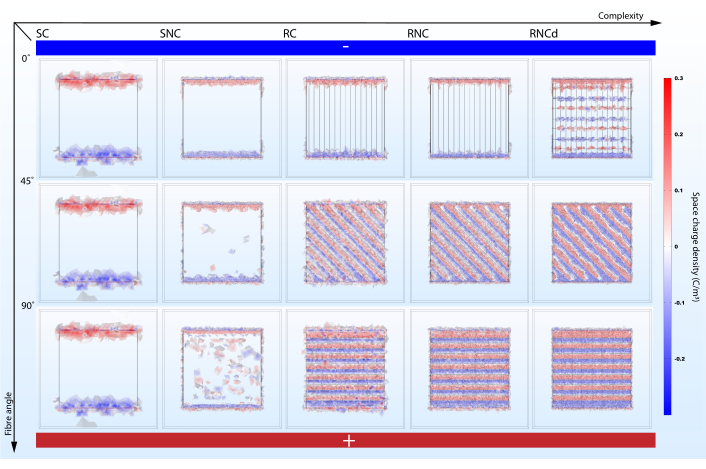
Figure 6: L’angle d’alignement de la fibre par rapport au gradient de potentiel électrique a un impact sur la densité de charge de l’espace dans les milieux de culture cellulaire environnants lorsque la complexité est suffisante. SC, SNC, RC, RNC et RNCd sont les différents niveaux de complexité pour le modèle de tapis fibreux présenté à la figure 3. L’axe vertical marque l’angle d’alignement des fibres par rapport au gradient de potentiel électrique. Électrodes abstraites présentées-côté inférieur à fort potentiel électrique et côté supérieur à faible potentiel électrique. Veuillez cliquer ici pour voir une version agrandie de cette figure.

Figure 7: Le mouvement de charge est influencé par l’alignement de la fibre de l’échafaudage par rapport à l’EF. Les deux panneaux illustrent les prédictions du modèle RNC à l’état d’équilibre. Sur le côté gauche, les fibres sont parallèles à l’EF, tandis que sur le côté droit, elles sont perpendiculaires. Le volume de couleur rouge clair à bleu marque la densité de charge, tandis que le volume de la flèche marque l’orientation de la densité actuelle. La couleur des flèches correspond à la norme de densité actuelle. Veuillez cliquer ici pour afficher une version agrandie de cette figure.

Nom	Expression	Description
Ws	10 * Rc * med_ratio	Largeur de l’échafa
Ls	10 * Rc * med_ratio	Longueur de l’échafa
Hs	2 * Rf	Hauteur de l’échafa
med_ratio	1.5	Rapport entre milieu de culture cellulaire et échafaudage
Rc	278,5[nm]	Rayon du noyau de la fibre
r	1.5	Rapport noyau de fibre / couche
Rf	Rc*r	Fibre avec rayon de couche
thêta	90[deg]	Angle d’orientation de la fibre
Si	1.3*(Ls*cos(thêta)+Ws*sin(thêta))	Longueur de la fibre
tes	1	Rapport entre le rayon du noyau de la fibre et la distance entre les fibres
n_1	2*(fix((Ws/(2*cos(thêta))-Rf)/(2*tes*Rc))+3)*(cos(thêta)!=0)+1*(cos(thêta)==0)	Nombre maximal de fibres si thêta< = 45
n_2	2*(fix((Ls/(2*sin(theta))-Rf)/(2*tes*Rc))+3)*(sin(theta)!=0)+1*(sin(theta)==0)	Nombre maximum de fibres si thêta>45
excès	1.2+0.3*abs(sin(2*thêta))	Premier décalage relatif de la fibre par rapport à l’échafaudage
D	Lf/5	Périodicité du manteau
appui	0.46	Longueur de la première couche par rapport à la périodicité D
E	100[mV/mm]	Magnitude du champ électrique
V0	E*Ls*med_ratio	Tension terminale
oméga	500[Hz]	Étude dépendante du temps Fréquence de tension
p_sigma	0.5	Conductivité relative du deuxième revêtement
p_eps	1.5	Deuxième constante diélectrique relative de revêtement

Tableau 1 : Paramètres utilisés pour la simulation

	Médias culturels	PEDOT:PSS 1	PEDOT:PSS 2	Collagène hydraté 1	Collagène hydraté 2	Fibroïne de soie	Collagène sec
Conductivité électrique (S/m)	1.7014	1.00E-01	p_sigma * 0,1	2.00E-05	p_sigma * 2e-5	1.00E-08	2.50E-08
Permittivité relative	80.1	2.2	p_eps * 2,2	9.89	p_eps * 9,89	7,81E+00	4.97

Tableau 2 : Propriétés des matériaux utilisées en simulation

Fichiers supplémentaires. Veuillez cliquer ici pour télécharger ce fichier.

Discussion

Le protocole proposé suggère une solution de modélisation uniforme pour les échafaudages naturels et artificiels et souligne la nécessité de prendre en compte la nanostructure des échafaudages fibreux lors de l’inspection des effets de l’EF sur les cellules ensemencées sur ces matériaux. Bien qu’une approximation grossière de l’intensité EF (différence de potentiel d’électrode divisée par la distance entre les électrodes) nous amène à nous attendre à une intensité de champ de 100 mV/mm, les simulations prédisent des intensités de champ stationnaires jusqu’à 30% plus élevées dans différentes zones du tapis(Figure 5). Ce résultat devrait être intéressant dans la conception des expériences ES et l’interprétation des données, car la mort cellulaire peut être causée par des FE trop forts. L’exposition du microenvironnement électrique permettrait une corrélation directe entre l’ES et le développement cellulaire. Bien que plusieurs études présentent une analyse morphologique détaillée des échafaudages utilisés^33,43,59, elles n’étudient pas l’interaction entre la structure, les propriétés électriques des matériaux et l’EF. Ce protocole peut permettre ce lien, car des paramètres tels que le rayon de la fibre, l’épaisseur de la couche de revêtement, la distance entre les fibres et les propriétés électriques des matériaux composants peuvent être modifiés en fonction de chaque expérience en modifiant les définitions globales aux étapes 1.2 et 1.3. Par conséquent, des prévisions de charge et de densité de courant personnalisées résolues spatialement en 3D peuvent être effectuées pour les régimes ES statiques et dynamiques.

L’optimisation de la conception des échafaudages peut être ciblée à travers les modèles RNC et RNCd avec de larges explorations de plage de paramètres, en mettant à l’échelle les morphologies proposées ou des parties de celles-ci. Alternativement, d’autres configurations d’échafaudage peuvent être étudiées avec le protocole proposé en changeant les types de réseau de linéaire à tridimensionnel dans la section 1.6.5 et en adaptant la géométrie de l’échafaudage dans la section 1.6.2. Cependant, l’optimisation de l’échafaudage ne peut se faire sans objectif. Alors qu’à des fins d’ingénierie tissulaire, l’accent est mis sur le devenir cellulaire, une image plus claire des stimuli qui sont ses principaux déterminants est essentielle si son contrôle fiable est souhaité. La charge et la densité de courant sont de bons descripteurs des microenvironnements électriques cellulaires car ils montrent l’interaction entre l’EF et les propriétés électriques des différents matériaux constitutifs d’échafaudages complexes tels que l’ECM. Le protocole montre comment calculer les prédictions pour ces métriques compte tenu d’une géométrie d’échafaudage nanofibreux et souligne l’importance de l’angle d’alignement des fibres avec l’EF. Les prédictions de la charge et de la densité de courant pourraient alors être liées au développement cellulaire et ainsi les régimes d’échafaudage et d’ES pourraient alors être optimisés pour des tâches spécifiques.

Fait intéressant, une étude montre que l’exposition à l’EF a généré une contrainte mécanique plus du double de résistance dans les films composites avec des nanofibres perpendiculaires à l’EF externe par rapport aux films à alignement parallèle⁶⁰. La contrainte mécanique rapportée pourrait être le résultat des forces de Coulomb agissant entre les fibres chargées, prédites par les simulations de modèles approximatifs (RC, RNC, RNCd)(Figure 6). Bien que ces simulations puissent être utiles pour étudier cette hypothèse, il convient de noter que les résultats expérimentaux rapportés ont été obtenus dans un système avec couplage capacitif, et la simulation présente un couplage direct.

Un facteur limitant les utilisations futures possibles du protocole pour estimer un signal d’entrée cellulaire est l’incertitude des paramètres. Les paramètres géométriques incertains sont l’épaisseur de la couche de revêtement et la distance entre les noyaux de fibres. La première pourrait être déduite en trouvant la valeur qui conduit à une impédance en vrac qui peut être validée expérimentalement. Le second peut être extrait à partir de scans de matériaux haute résolution. Les paramètres décrivant les propriétés physiques des matériaux sont également affectés par l’incertitude. Cependant, la conductivité électrique et la constante diélectrique des matériaux illustrés diffèrent beaucoup plus que la précision de mesure expérimentale(tableau 2). Par conséquent, les effets déclarés seraient maintenus malgré des erreurs de mesure modérées.

Les résultats montrent qu’une complexité de modèle pas suffisante peut masquer des informations pertinentes. Il est important de reconnaître que le protocole simule une version simplifiée du phénomène physique en cours car il ne tient pas compte de la nature différente des matériaux impliqués dans le processus - conducteur (électrodes), semi-conducteur (revêtement), diélectrique (noyaux de fibres) et électrolytique (substance environnante) - qui sont capables d’influencer le transport de charge. Ce problème peut être pris en compte dans les futures expansions de modèles en ajoutant des retards de transfert d’énergie aux interfaces (c’est-à-dire des réactions faradiques) et des retards de transport d’ions dans l’électrolyte. L’ajout de complexité devrait cependant être guidé par une validation expérimentale, car un modèle simple qui reproduit la plupart de ce qui est observé est plus utile qu’un modèle remarquablement précis qui ajoute un peu plus d’informations mais qui est profondément sensible à l’incertitude de nombreux paramètres constitutifs.

Comme l’objectif final de l’ingénierie tissulaire est de créer des bioréacteurs qui non seulement imitent un ou deux aspects des environnements in vivo, mais reproduisent et contrôlent tous les indices de développement cellulaire^61,les modèles électromagnétiques et mécaniques in silico ainsi que les modèles de transfert de chaleur entre les composants du bioréacteur devront être combinés. Dans une phase de modélisation ultérieure, des phénomènes de couplage entre ces interactions tels que le chauffage ohmique, l’écoulement de fluide électrolytique, les déformations morphologiques de l’échafaudage en réponse à la stimulation électrique⁶⁰ et la piézoélectricité⁶² peuvent également être ajoutés. Cependant, les modèles ne doivent être fusionnés qu’après que chacun d’eux a été validé expérimentalement. De cette façon, nous pouvons mieux comprendre l’influence de chaque composant dans le microenvironnement cellulaire et comment les stimuli peuvent être optimisés.

Si le modèle proposé est validé expérimentalement, il peut être combiné avec des modèles de cellules biologiques - Figure 1. Les modèles de densité de charge et les modulations pourraient influencer de manière asymétrique l’activité de pompes ioniques spécifiques, impacter l’attachement à la fibre des protéines entraînant l’adhésion de la membrane⁶³ et donc guider la migration, les modèles de prolifération et la morphogenèse^64. L’exploration de ces hypothèses est la voie à suivre pour comprendre les mécanismes qui sous-tendent les réponses des tissus et des cellules aux SE.

matériels

Name	Company	Catalog Number	Comments
Comsol multiphysics 5.2 AC/DC module	COMSOL	-	FEM modelling software