JoVE Logo
АВТОРЫ
СВЯЖИТЕСЬ С НАМИ

Войдите в систему

В этой статье

  • Резюме
  • Аннотация
  • Введение
  • протокол
  • Результаты
  • Обсуждение
  • Раскрытие информации
  • Благодарности
  • Материалы
  • Ссылки
  • Перепечатки и разрешения

Резюме

В данной работе представлена стратегия построения конечно-элементных моделей волокнистых проводящих материалов, подвергающихся воздействию электрического поля (EF). Модели могут быть использованы для оценки электрического входа, который получают клетки, засеянные в таких материалах, и оценки влияния изменения свойств, структуры или ориентации составляющего материала каркаса.

Аннотация

Клинические исследования показывают, что электрическая стимуляция (ЭС) является потенциальной терапией для заживления и регенерации различных тканей. Таким образом, понимание механизмов клеточного ответа при воздействии электрических полей может направлять оптимизацию клинических применений. Эксперименты in vitro направлены на то, чтобы помочь выявить их, предлагая преимущество более широких диапазонов ввода и вывода, которые могут быть этически и эффективно оценены. Тем не менее, достижения в экспериментах in vitro трудно воспроизвести непосредственно в клинических условиях. Главным образом, это связано с тем, что устройства ES, используемые in vitro, значительно отличаются от тех, которые подходят для использования пациентами, а путь от электродов к целевым клеткам отличается. Поэтому перевод результатов in vitro в процедуры in vivo не является простым. Мы подчеркиваем, что структура и физические свойства клеточной микросреды играют определяющей роль в реальных условиях экспериментального тестирования, и предполагаем, что меры распределения заряда могут быть использованы для преодоления разрыва между in vitro и in vivo. Рассматривая это, мы показываем, как в силико-конечно-элементное моделирование (МКЭ) может быть использовано для описания клеточной микросреды и изменений, генерируемых воздействием электрического поля (EF). Мы расскаем, как EF связывается с геометрической структурой для определения распределения заряда. Затем мы показываем влияние зависящих от времени входов на движение заряда. Наконец, мы демонстрируем актуальность нашей новой методологии модели in silico с использованием двух тематических исследований: (i) in vitro волокнистый поли(3,4-этилендиокситиофен) поли(стиронесульфонат) (PEDOT-PSS) каркасы и (ii) коллаген in vivo во внеклеточном матриксе (ECM).

Введение

ES - это использование ЭФ с целью контроля биологических клеток и тканей. Его механизм основан на физическом стимуле, трансдуцированном в клетку, когда биомолекулы внутри и вокруг нее подвергаются воздействию внешне генерируемого градиента напряжения. Заряженные частицы участвуют в организованном движении, управляемом законом Кулона, создавая силы сопротивления на незаряженных частицах. Результирующий поток жидкости и распределение заряда изменяют активность и функции клеток, такие как адгезия, сокращение, миграция, ориентация, дифференцировка и пролиферация1, поскольку клетка пытается адаптироваться к изменениям условий микросреды.

Поскольку ЭФ являются контролируемыми, неинвазивными, нефармакологическими и, как показано, оказывают эффективное влияние на поведение основных клеток, ЭС является ценным инструментом для тканевой инженерии и регенеративной медицины. Он был успешно использован для руководства развитием нервной2,скелетной3,сердечной мышцы4,кости5 и кожи6. Более того, поскольку он усиливает ионофорез7,он используется в качестве альтернативного или дополнительного лечения к обычным фармакологическим. Его эффективность в лечении боли все еще обсуждается, поскольку ожидается более высокое качество клинических испытаний8,9,10. Тем не менее, не было зарегистрировано никаких побочных эффектов, и это может улучшить благосостояние пациентов11,12,13,14,15.

В то время как только клинические испытания могут дать окончательный вердикт об эффективности процедуры, модели in vitro и in silico необходимы для информирования о разработке предсказуемого лечения ЭС, поскольку они предлагают более сильный контроль над более широким спектром экспериментальных условий. Исследуемыми клиническими применениями ЭС являются регенерация костей16,17,восстановление денервированных мышц18,19,аксональная регенерация после операции20,21,обезболивание22,заживление ран23,24,25 и доставка ионофоретического препарата26. Для того, чтобы устройства ES были широко внедрены во всех возможных целевых приложениях, клинические испытания еще не установили более убедительных доказательств эффективности лечения. Даже в областях, где исследования in vivo на животных и людях постоянно сообщают о положительных результатах, большое количество зарегистрированных методов в сочетании со слишком малым количеством указаний о том, как выбирать между ними, и высокой ценой приобретения удерживает клиницистов от инвестирования в устройства ES27. Чтобы преодолеть это, ткань-мишень больше не может рассматриваться как черный ящик (предел экспериментов in vivo), а должна рассматриваться как сложная синергия нескольких подсистем(рисунок 1).

Многочисленные эксперименты с ЭС были проведены in vitro в течение28,29,30,31,32,33,34лет. Большинство из них характеризуют ЭС только через падение напряжения между электродами, деленное на расстояние между ними - грубое приближение величины электрического поля. Однако само электрическое поле воздействовало только на заряженные частицы, а не на клетки напрямую. Кроме того, когда между устройством и ячейками вставляются несколько материалов, грубое приближение может не удерживаться.

Лучшая характеристика входного сигнала требует четкого представления о том, как стимул трансдуцируется в клетку. Основными способами доставки ЭС являются прямая, емкостная и индуктивнаясвязь 35,36. Устройства для каждого способа различают по типу электрода (стержень, планар или обмотка) и размещению относительно ткани-мишени (контактной или изолированной)35. Устройства, используемые in vivo для более длительных процедур, должны быть носимыми, поэтому электроды и в большинстве случаев источник энергии либо имплантируются, либо прикрепляются к коже в виде раневых повязок или электроактивных пластырей. Генерируемый градиент напряжения вытесняет заряженные частицы в зоне обработки.

Поскольку структура каркаса влияет на результирующий поток заряженных частиц в непосредственной близости от ячеек, она имеет первостепенное значение при разработке протоколов ES. Различные конфигурации переноса заряда возникают при изменении материала платформы, метода синтеза, структуры или ориентации относительно градиента напряжения. In vivo на доступность и движение заряженных частиц влияют не только клетки, но и коллагеновая сеть и интерстициальная жидкость, составляющая поддерживающий ECM. Инженерные каркасы все чаще используются для лучшего воссоздания естественных клеточных микросред in vitro1,35. В то же время ECM представляет собой сложный естественный каркас.

Искусственные леса основаны на металлах, проводящих полимерах и углероде, спроектированы с акцентом на балансировку биосовместимости с электрохимическими характеристиками и долгосрочной стабильностью36. Одним из универсальных типов каркасов является электрорасплесковый волокнистый мат, который предлагает контролируемую наноразмерную топографию. Это может быть спроектировано так, чтобы напоминать ECM, таким образом, доставлять аналогичные механические сигналы, которые помогают регенерации широкого спектра тканей37. Чтобы значительно повлиять на ES, коврики должны быть в некоторой степени проводящими. Однако проводящие полимеры трудно электроспинировать и смешивание с изолирующими носителями ограничивает проводимость полученных волокон38. Одним из решений является полимеризация проводящего мономера на поверхности диэлектрического волокна, что приводит к хорошей механической прочности и электрическим свойствам конечного продукта38. Примером может быть покрытие шелковых электропрядных волокон полупроводящим PEDOT-PSS39. Сочетание механических и электромагнитных сигналов значительно ускоряет рост нейритов40,41,42. Нейриты следуют за выравниванием волокон каркасов и удлиняются больше после воздействия EF параллельно волокнам, чем вертикального43. Аналогичным образом, выравнивание волокнистых каркасов к EF также способствует миогенному созреванию33.

ECM в основном состоит из волокнистых белков44,из которых коллаген типа I является основным компонентом во всех тканях животных, кроме хряща (богатого коллагеном типа II)44. Тропоколлаген (TC), тройная спиральная конформация полипептидных нитей, является структурным мотивом коллагеновых фибрилл45. Просвечивающая электронная микроскопия и атомно-силовая микроскопия изображений коллагеновых фибрилл показывают D-периодический полосатый паттерн46, объясненный моделью Ходжа и Петруски47 как регулярные массивы TC зазоров и перекрытий45. Сухожилия состоят из выровненной коллагеновой фибриллярной матрицы, экранированной неколлагеновой высокогидрофильной протеогликановой матрицей48,49. Декорин представляет собой небольшой богатый лейцином протеогликан (SLRP), способный связывать области разрыва коллагеновых фибрилл и соединяться с другими SLRP через их боковые цепи гликозаминогликана (GAG)49. Исследования, проведенные на сухожилиях, показывают, что их электрические свойства значительно изменяются при гидратации50,51,механизм переноса заряда изменяется от протонического к ионическому по мере повышения уровня гидратациина 51. Это говорит о том, что электрическая проводимость вдоль фибриля коллагенового типа I может быть включена с помощью слоя Декорин-вода, с зазорами и перекрывающимися областями, имеющими различную электрическую проводимость и диэлектрические постоянные.

Поскольку идентичное воссоздание ECM искусственными каркасами невероятно, знания, создающие синергию между in vivo и in vitro, обеспечиваемые переводимыми результатами, похоже, зайдут в тупик. Моделирование in silico не только позволяет повторно транслировать между ними, но и добавляет важные преимущества в характеристике неизвестных процессов, связанных с ES. Сравнение наблюдений in vivo с наблюдениями in vitro может принести информацию о силе связи между тканью-мишенью и остальной частью организма, но не раскрывает текущих пределов знаний. Неизвестное можно разоблачить, наблюдая разницу между тем, что ожидается на основе текущих знаний, и тем, что происходит. Эксперименты in silico, основанные на математическом моделировании, позволяют разделить процесс на известные и неизвестные подпроцессы. Таким образом, явления, не учтенные в модели, выявляются, когда прогнозы in silico сравниваются с экспериментами in vitro и in vivo.

Формированию и проверке гипотез относительно основного механизма (механизмов) того, как клетки и ткани подвергаются воздействию электрических полей, препятствует большое количество параметров52, которые необходимо проверить отдельно. Чтобы определить репрезентативные экспериментальные условия, процесс ES должен быть разделен на подпроцессы(рисунок 1)и должны быть идентифицированы доминирующие входные сигналы, влияющие на поведение клеток. Модели, представляющие фундаментальные физические эффекты ЭС на клетки, описывают область, которая связывает EF с клеткой - область заряженных частиц53. Поведение частиц по отношению к клетке зависит от микросреды и может быть исследовано отдельно от клетки. Доминирующим входным сигналом для ячейки является подмножество выходов устройства ES, которое вызывает наибольшую степень изменчивости в реакции клетки. Наименьшее подмножество полных экспериментальных параметров, которое может генерировать вариации во всех доминирующих входных сигналах ячейки, может быть использовано для уменьшения размерности пространства параметров и количества тестовых случаев.

Входные данные биологической целевой модели ES должны представлять собой подмножество выходных сигналов, производимых устройством ES, которые полезны для описания физического воздействия ES на клетки. Простой биореактор с прямой связью имеет ту же структуру, что и электролитические электрохимические элементы. Модели из них показывают первичное (с учетом сопротивления раствора), вторичное (также учитывая фарадические реакции) или третичное (также учитывая диффузию ионов) распределение плотности тока. Поскольку сложность приводит к вычислительной стоимости, простейшая модель наиболее подходит для исследования параметров космоса. Моделирование волокнистых композитов, мотивированных свойствами материала54, фокусируется на свойствах сыпучих материалов в результате сложной микроамхитектерии, следовательно, не может описывать локальные эффекты воздействия EF. Существующие в силико модели, мотивированные ES, фокусируются на биологическом образце, будь то одна клетка, погруженная в однороднуюсреду 55,56,57,или сложные ткани с однородным внеклеточным пространством58. Плотность заряда и тока(рисунок 2)могут выступать в качестве интерфейсных сигналов между моделями устройства ES и биологическим образцом или между различными компонентами устройства ES. Предлагаемый протокол на основе МКЭ использует уравнения, описанные на рисунке 2, и был использован для изучения того, как зависящие от каркаса параметры могут быть использованы для модуляции этих двух сигналов, независимо от EF, генерируемого установкой прямой связи. Результаты подчеркивают, что необходимо учитывать электрические свойства каркаса или ECM при исследовании того, как ES влияет на клетки-мишени.

протокол

1. Построение модели в COMSOL

  1. Откройте COMSOL и выберите Пустая модель.
  2. Параметры: В Model Builderщелкните правой кнопкой мыши глобальные определения,выберите Параметрыи добавьте параметры в соответствии с таблицей 1.
  3. Материалы: Добавьте материалы со свойствами согласно таблице 2.
    1. В построителе моделей в разделе Глобальные определениящелкните правой кнопкой мыши Материал и выберите Пустой материал.
    2. Добавить свойства материала: в настройках вновь добавленного материала разверните узел Свойства материала > Основные свойства,выберите Относительная проницаемость и нажмите символ '+', чтобы добавить свойство. Повторите шаг для Параметра Электропроводность.
    3. В разделе Содержание материалазаполните текущие свойства материала в соответствии с таблицей 2.
  4. Определение компонента: на вкладке Главная верхней ленты щелкните левой кнопкой мыши Добавить компонент и выберите 3D. Новый узел компонента появится в построителе моделей.
  5. Геометрия: В конструкторе моделейщелкните правой кнопкой мыши Геометрия,щелкните левой кнопкой мыши вставить,дважды щелкните полную модель и выберите соответствующую последовательность (SC / SNC / RC / RNC / RNCd).
  6. Кроме того, можно построить геометрию с нуля, следуя подчиненным шагам.
    1. В построителе моделейщелкните левой кнопкой мыши Пункт Геометрия под текущим узлом компонента. Тот же узел Geometry будет указан в следующих подчиненных шагах. В окне Настройка измените единицу измерения Длина на нм и убедитесь, что флажок "Масштабировать значения при смене единиц измерения" не установлен.
    2. Геометрия строительных лесов
      1. В конструкторе моделейщелкните правой кнопкой мыши геометрию и выберите Блок.
      2. На вкладке Настройки заполните метку "Экстенты скаффота".
      3. Разверните узел Размер и форма и заполните "Ws", "Ls", "Hs" для ширины, глубины и высоты.
      4. Разверните положение и измените базу на центральную.
      5. Разверните узел Выбор результирующих сущностей,выберите Создать и добавьте "Выбор скафафота".
    3. Экстента окружающего вещества: в конструкторе моделейв разделе Геометриящелкните правой кнопкой мыши Экстенты scaffold и выберите Дублироватьи редактировать вкладку Настройки.
      1. Измените метку на "Медиа экстенты".
      2. К каждому блоку в разделе Размер и Shape добавьте "med_ratio *" перед существующим параметром.
      3. В области Выбор результирующих сущностейдобавьте Новый выбор как "Выбор мультимедиа".
    4. Геометрия волокна (SC пропустить до 1.6.6)
      1. Ядро (RC пропустить до 1.6.4.2)
        1. В построителе моделейщелкните правой кнопкой мыши Геометрия,выберите Цилиндри отредактируйте вкладку Параметры следующим образом.
        2. Измените метку на "Ядро".
        3. Разверните узел Размер и Форма и заполните "Rc" и "Lf" для радиуса и высоты.
        4. Разверните положение Положение и заполните "-избыток*Ws/2" и "-Lf/2" для x и y.
        5. Разверните ось и измените тип оси на ось Y.
        6. Разверните раздел Выбор результирующих сущностей и добавьте "Основной выбор".
      2. Пальто (SNC пропустить до 1.6.5)
        1. Плита (RC или RNC пропустить до 1.6.4.2.2; RNCd пропустить к 1.6.4.2.3)
          1. В построителе моделей в разделе Геометриящелкните правой кнопкой мыши экстентные области scaffold и выберите Дублировать. Убедитесь, что дубликат (экстенты Scaffold 1) находится сразу после Core в последовательности геометрии.
          2. На вкладке Настройки измените метку на "Пальто".
          3. На вкладке «Настройки» разверните узел «Выбор результирующих сущностей» и создайте «Выбор волокна».
          4. Перейти к 1.6.5.
        2. Однородный
          1. В конструкторе моделей щелкните правой кнопкой мыши Геометрия,выберите Цилиндр и отредактируйте вкладку Настройки следующим образом.
          2. Измените метку на "Пальто".
          3. Разверните узел Размер и Форма и заполните поля "Rf" и "Lf" для параметров Радиус и Высота.
          4. Разверните положение Положение и заполните "-избыток*Ws/2" и "-Lf/2" для x и y.
          5. Разверните ось и измените тип оси на ось Y (RC пропустить до 1.6.4.2.2.7).
          6. Разверните слои,заполните "Rf-Rc" для параметра Толщина и оставьте флажок "Слои сбоку".
          7. Разверните выделение результирующих сущностей и добавьте «Выбор слоя» или, для RC, «Выбор волокна» (RC пропустить до 1.6.5).
          8. В построителе моделейщелкните правой кнопкой мыши Геометрия и выберите Удалить сущности.
          9. На вкладке Настройки измените Геометрический начальный уровень на Домен и выберите Выбор пальто для Выбора.
          10. Удалите все домены, кроме домена 3, из поля выбора (ядро слоистого цилиндра).
          11. Разверните узел Выделения результирующих сущностей и выберите Выделение слоя.
          12. Перейти к 1.6.5.
        3. Периодический массив двух типов
          1. В конструкторе моделейщелкните правой кнопкой мыши Геометрия и выберите Цилиндр. Щелкните правой кнопкой мыши созданный элемент и выберите Дублировать. Отредактируйте вкладку Настройки следующим образом.
            1. Установите метку на "Пальто 1" / "Пальто 2".
            2. Установите радиус в Rf.
            3. Установите высоту "D*prop"/"D*(1-prop)".
            4. Разверните позицию и заполните "-excess*Ws/2" как для x, так и для "-Lf/2"/"-Lf/2+D*prop" для y.
            5. Разверните ось и измените тип оси на ось Y.
            6. Разверните раздел Слои и заполните "Rf-Rc"; Убедитесь, что установлен флажок "Слои сбоку".
            7. Разверните выделенные объекты и создайте «Выбор пальто 1» / «Выбор пальто 2».
          2. В построителе моделейщелкните правой кнопкой мыши Геометрия и выберите Удалить сущности.
            1. На вкладке Настройки измените Геометрический начальный уровень на Домен и выберите цилиндр 2 (cyl2) и цилиндр 3 (cyl3) в графическом окне.
            2. Удалите из поля выбора все домены, кроме домена 3 (ядро слоистых цилиндров).
            3. Разверните выделенные элементы результирующих сущностей и создайте параметр «Выделение слоя».
          3. В построителе моделейщелкните правой кнопкой мыши Геометрия, разверните узел Преобразования и выберите Массив. Вкладка "Изменить настройки" выглядит следующим образом.
            1. Выберите «Выбор слоя» для входных объектов.
            2. Задайте для типа Массив значение Линейный.
            3. Установите для параметра Размер значение "Lf/D".
            4. Установите для установки для установки для оси y значение "D".
    5. Геометрия ориентированного волоконного массива
      1. Массив ядра (RC пропустить до 1.6.5.2)
        1. В построителе моделейщелкните правой кнопкой мыши Геометрия, разверните преобразования и выберите Повернуть.
          1. На вкладке Параметры включите переключатель Входные объекты и выберите Выбор ядра из раскрывающегося списка. Убедитесь, что флажок Хранить входные объекты не установлен.
          2. Разверните угол поворота и заполните "тета" для параметра "Поворот".
          3. Разверните выделенные элементы результирующих сущностей и создайте «Выбор волокон».
        2. В построителе моделей щелкните правой кнопкой мыши Геометрия, разверните преобразования и выберите Массив.
          1. Измените метку на "Core Array".
          2. Выберите Основной выбор в раскрывающемся списке для входных объектов.
          3. Разверните узел Размер, измените тип массива на Линейный и заполните "n_1*(theta<=45) +n_2*(theta>45)" в параметре Размер.
          4. Разверните смещение и заполните "2*tes*Rc*cos(theta)", "2*tes*Rc*sin(theta)" для x и y.
          5. Разверните выделенные элементы результирующих сущностей и выберите «Выбор волокна».
      2. Coat Array (SNC пропустить до 1.6.5.3)
        1. В построителе моделейщелкните правой кнопкой мыши Геометрия, разверните преобразования и выберите Повернуть.
          1. На вкладке Настройки включите переключатель Входные объекты и выберите в раскрывающемся списке Пункт Выбор пальто. Убедитесь, что флажок "Хранить входные объекты" не установлен.
          2. Разверните угол поворота и заполните "тета" для параметра "Поворот".
          3. Разверните выделенные элементы результирующих сущностей и выберите «Выбор волокна».
        2. В построителе моделейщелкните правой кнопкой мыши Геометрия, разверните преобразования и выберите Массив.
          1. Измените метку на "Coat Array".
          2. Выберите «Выделение слоя» в раскрывающемся списке для входных объектов.
          3. Разверните узел Размер, измените тип массива на Линейный и заполните "n_1*(theta<=45) +n_2*(theta>45)" в параметре Размер.
          4. Разверните смещение и заполните "2*tes*Rc*cos(theta)", "2*tes*Rc*sin(theta)" для x и y.
          5. Разверните выделенные элементы результирующих сущностей и выберите «Выбор волокна».
      3. Вырезанные леса
        1. Объединение волокон: в конструкторе моделей щелкните правой кнопкой мыши Геометрия, разверните логические значения и разделы и выберите Объединить.
          1. Измените метку на "Волокна".
          2. Включите переключатель Входные объекты и выберите Выбор оптоволокна из раскрывающегося списка.
          3. Убедитесь, что флажок "Хранить входные объекты" не установлен.
          4. Убедитесь, что установлен флажок «Сохранять внутренние границы».
          5. Разверните узел Выбор результирующих сущностей и выберите Выбор скаффолдов в раскрывающемся списке.
        2. Выполнить вырезание: в конструкторе моделей щелкните правой кнопкой мыши Геометрия, разверните логические значения и секции и выберите Пересечение.
          1. Измените метку на "Строительные леса".
          2. Включите переключатель Входные объекты и выберите Выбор скафафлей из раскрывающегося списка.
          3. Убедитесь, что флажок "Хранить входные объекты" не установлен.
          4. Убедитесь, что установлен флажок «Сохранять внутренние границы».
    6. Геометрия ансамбля
      1. Определите геометрию окружающего вещества.
        1. В построителе моделейщелкните правой кнопкой мыши Геометрия,разверните логические значения и секции и выберите Разница. Перейдите на вкладку Настройки.
        2. В раскрывающемся списке Объекты для добавления выберите Выбор мультимедиа.
        3. В раскрывающемся списке Объекты для вычитания выберите Выбор скафафота.
        4. Убедитесь, что установлены флажки «Сохранять входные объекты» и «Сохранять внутренние границы».
      2. Поле Удалить экстент мультимедиа.
        1. В построителе моделейщелкните правой кнопкой мыши Геометрия и выберите Удалить сущности. Перейдите на вкладку Настройки.
        2. Выберите Домен в раскрывающемся списке Геометрический начальный уровень.
        3. Выберите Выбор мультимедиа в раскрывающемся списке Выбор.
        4. Удалите "dif1" из поля выбора.
    7. Геометрия сборки
      1. В узле Геометрия убедитесь, что последним элементом перед узлом Кумулятивный выбор является Объединение форм, а не Сборка формы. При необходимости щелкните правой кнопкой мыши Сборка формы и измените действие на "Сформировать объединение" на вкладке Настройки.
      2. В построителе моделейщелкните левой кнопкой мыши Геометрия и выберите Построить все.
  7. Материалы
    1. В построителе моделей в узле Текущий компонент щелкните правой кнопкой мыши Материалы и выберите Ссылка на материал.
    2. Повторите раздел пять раз, столько же материалов рассматривается в соответствии с уровнем сложности.
    3. Ассоциируемые материалы для каждого компонента в следующем порядке: окружающее вещество, слои, сердечник.
    4. На вкладке Параметры выберите Медиа/Скаффолд (для SC, SNC, RC)/Покрытие/Выбор ядра из раскрывающегося списка Выбор.
    5. Разверните настройки ссылок и выберите соответствующий материал из раскрывающегося списка.
  8. Объединение
    1. В построителе моделейщелкните левой кнопкой мыши узел Mesh под текущим компонентом.
    2. На вкладке Параметры выберите Обычный в раскрывающемся списке Размер элемента и щелкните левой кнопкой мыши Построить все.
  9. Физика: В model Builderщелкните левой кнопкой мыши текущий компонент, выберите Добавить физику,разверните модуль AC/DC на вкладке Добавить физику, выберите модуль Электрические токи (ec) и нажмите кнопку Добавить в компонент.
    1. Граничные условия: на вкладке Графика выберите представление xy.
      1. Земля: в конструкторе моделейщелкните правой кнопкой мыши узел Электрические токи и выберите Земля.
      2. Убедитесь, что переключатель выделения для выбора границ активен, и щелкните левой кнопкой мыши на самой высокой окружающей стороне вещества, параллельной плоскости xz, чтобы добавить границу 5 в поле выбора границы.
      3. Терминал: В конструкторе моделейщелкните правой кнопкой мыши узел Электрические токи и выберите Терминал.
      4. Убедитесь, что переключатель выделения для выбора границ активен, и щелкните левой кнопкой мыши на самой нижней окружающей стороне вещества, параллельно плоскости xz, чтобы добавить границу 2 в поле выбора границы.
      5. Разверните раздел Терминал и выберите Напряжение в выпадающем списке Тип терминала; заполните V0 для Voltage.
    2. При необходимости добавьте сложность: Сохраните текущий компонент и вернитесь к шагу 1.4, чтобы следовать другому пути сложности (SC/SNC/RC/RNC/RNCd).

2. Выполните моделирование

  1. Адаптивное уточнение сетки
    1. В Model Builderщелкните левой кнопкой мыши корневой узел модели и выберите Добавить исследование, чтобы открыть вкладку Добавить исследование, выберите Стационарное исследование и щелкните правой кнопкой мыши кнопку Добавить исследование.
    2. Создайте шаг исследования для каждого созданного компонента: в узле Исследование щелкните правой кнопкой мыши Шаг 1: Стационарное исследование и выберите Дублировать.
    3. Для каждого шага исследования измените вкладку настроек с деталями соответствующего компонента.
      1. Развернуть выбор физики и переменных; в столбце Решить для оставьте флажок только текущий компонент.
      2. Разверните узел Расширения исследования и установите флажок Адаптивное уточнение сетки.
      3. Выберите геометрию текущего компонента из раскрывающегося списка рядом с пунктом Адаптация в геометрии.
    4. В построителе моделей щелкните правой кнопкой мыши Исследование 1 и выберите Вычисления. Это позволит создать адаптированные сетки для геометрии всех компонентов с их текущим углом ориентации.
  2. Установите угол ориентации и выполните стационарное исследование.
    1. В конструкторе моделейв разделе Глобальные определениящелкните левой кнопкой мыши Параметры и измените параметр тета на угол ориентации волокна, необходимый для моделирования.
    2. Для каждого компонента в построителе моделей разверните узел компонента, щелкните правой кнопкой мыши Геометрия и выберите Построить все.
    3. В построителе моделейщелкните правой кнопкой мыши адаптивное исследование уточнения сетки и выберите вычисления.
    4. В Model Builder щелкните левой кнопкой мыши корневой узел модели и выберите Добавить исследование, чтобы открыть вкладку Добавить исследование, выберите Стационарное исследование и щелкните правой кнопкой мыши кнопку Добавить исследование.
    5. В Model Builderпод недавно добавленным исследованием щелкните левой кнопкой мыши Шаг 1,разверните выделение сетки и для каждого компонента выберите сетки, созданные в исследовании адаптивного уточнения сетки.
    6. Щелкните правой кнопкой мыши кнопку Вычисления.
  3. Установите угол ориентации, входной сигнал и выполните зависящий от времени исследование.
    1. В конструкторе моделейв разделе Глобальные определениящелкните левой кнопкой мыши Параметры и измените параметр тета на угол ориентации волокна, необходимый для моделирования.
    2. В построителе моделейщелкните левой кнопкой мыши корневой узел модели и выберите Добавить исследование, чтобы открыть вкладку Добавить исследование. Выберите «Исследование, зависящей от времени»,нажмите левой кнопкой мыши кнопку «Добавить исследование» и отредактируйте вкладку «Настройки» следующим образом.
      1. Установите время на "диапазон(0, (2*пи/омега)/39,2*пи/омега)".
      2. Развернуть выбор физики и переменных; оставьте флажок "Решить для" только компонент моделирования.
      3. Разверните узел Выделение сетки и выберите сетку для компонента моделирования. Измените сетки других компонентов на No mesh.
      4. Разверните узел Расширения исследования и установите флажок Адаптивное уточнение сетки; выберите геометрию компонента моделирования из выпадающего списка.
    3. Определите зависящие от времени граничное условие.
      1. В узле текущего компонента щелкните правой кнопкой мыши Определения и в разделе Функции выберите Форма сигнала.
      2. На вкладке Настройки измените название функции на "Ввод".
      3. Разверните параметры , установите для параметра Тип значение Синус,для параметра Угловая частота — значение "омега", для параметра Амплитуда — значение V0.
      4. Для компонента моделирования под его узлом «Электрические токи» выберите «Клемма» и измените напряжение на «Вход(t[1/s])».
    4. Щелкните правой кнопкой мыши кнопку Вычисления.

3. Анализ

  1. Плотность заряда
    1. В узле Результаты щелкните правой кнопкой мыши построитель моделей выберите Группа 3D-графиков и измените параметры.
      1. Измените метку на "Плотность заряда".
      2. Разверните узел Данные и выберите набор данных параметрического исследования в раскрывающемся списке Набор данных.
      3. Разверните цветовую легенду и установите флажки «Показать легенды» и «Показать максимальные и минимальные значения».
    2. Щелкните правой кнопкой мыши Плотность заряда в узле Результаты в построителе моделей и выберите Том; перейдите на вкладку Редактирование настроек.
      1. Разверните узел Данные и выберите "От родительского" в раскрывающемся списке Набор данных.
      2. Разверните узел Выражение и заполните поле "ec.rhoq" в поле Выражение.
      3. Разверните узел Диапазон и установите флажок Ручной цветовой диапазон.
        1. Установите минимум на "-0,03", а максимум на "0,03".
      4. Разверните узел Раскраска и стиль,установите для параметра Coloring значение Color table, для Color table ( Волна , установите флажок Легенда цвета, установите флажок Симметризировать цветовой диапазон.
      5. Щелкните правой кнопкой мыши Том в построителе моделей и выберите Фильтр.
        1. На вкладке Настройки введите "abs(ec.rhoq)>0.012" в логическом выражении для включения.
    3. Щелкните левой кнопкой мыши кнопку «График», чтобы визуализировать результаты в графическом окне.
  2. Плотность тока
    1. В построителе моделей щелкните правой кнопкой мыши узел Результаты, выберите Группа 3D-графиков и отредактируйте вкладку Параметры.
      1. Измените метку на "Плотность тока".
      2. Разверните узел Данные и выберите набор данных параметрического исследования в раскрывающемся списке Набор данных.
      3. Разверните цветовую легенду,установите флажки «Показать легенды» и «Показать максимальные и минимальные значения».
    2. Щелкните правой кнопкой мыши Плотность тока в узле Результаты в построителе моделей и выберите Громкость стрелки; перейдите на вкладку Редактирование настроек.
      1. Разверните узел Данные и выберите "От родительского" в раскрывающемся списке Набор данных.
      2. Разверните выражение и заполните "ec. Jx", "эк. Jy", "ec. Jz" в полях Выражение для компонентов x, y и z соответственно.
      3. Разверните узел Расположение стрелки и заполните 20 для всех координат количество точек.
      4. Разверните узел Раскраска и стиль,установите для параметра Длина стрелки значение Нормализовано, для основания стрелки — значение По центру, установите флажок Коэффициент масштабирования и установите значение 85.
      5. Щелкните правой кнопкой мыши Громкость стрелки в построителе моделей и выберите Цветовое выражение.
        1. На вкладке Настройки введите "ec.normJ" в поле Выражение.
        2. Разверните узел Раскраска и стиль,установите для таблицы цветов значение Трафик, установите флажки Легенда цвета и Обратная таблица цветов.
    3. Нажмите на кнопку «График», чтобы визуализировать результаты в графическом окне.

Результаты

Предложенная модель описывает особенности композитного мата с параллельными волокнами, погруженного в проводящее вещество и подвергающегося воздействию внешне генерируемого градиента электрического потенциала. Моделирование показывает, что учет различных компонентов каркаса важен в микромасштабе, и исследует, как изменение угла выравнивания (входного сигнала) волокон к EF может генерировать изменчивость тока и плотности заряда (выходные сигналы) в непосредственной близости от волокон.

Представлены пять различных стадий геометрической сложности, каждая из которых влияет на результат моделирования: гладкая проводячая плита (SC), гладкая плита с непроводящими встроенными волокнами (SNC), грубый проводящий композит (RC), грубый композит с непроводящими встроенными волокнами (RNC), грубый композит с непроводящими встроенными волокнами и два типа периодического покрытия (RNCd)(рисунок 3). В разделе 1.5 протокола представлены шаги по импорту геометрий в проекте, а в разделе 1.6 показано, как их пошагово построить. Первые две модели не учитывают морфологию поверхности. SC и RC не учитывают диэлектрические свойства волоконной сердечника. RNC является предлагаемой моделью для нановолокнистых искусственных лесов, в то время как RNCd является предлагаемой моделью для сегмента ECM.

Минимизация вычислительных затрат была достигнута за счет сведения геометрии устройства ES к объему единицы модели, представляющей микросреду. В то время как ширина и длина устройства ES и каркаса могут легко составлять порядка нескольких сантиметров, диаметр содержащих волокон обычно ниже микрона. Здесь мы используем разрез каркаса, сопоставимый с диаметром волокна, чтобы снизить вычислительные затраты, вызванные соотношением сторон, и подчеркнуть влияние волокнистой природы каркаса на электрическую микросреду. Остальная часть устройства ES заменяется граничными условиями электрического потенциала, выбранными таким образом, что грубое приближение величины электрического поля составляет 100 В/м, часто сообщаемый параметр стимуляции. Более того, единичный объем с пятью параллельными волокнами, как тот, который используется в моделировании, представленном на рисунке 3, предполагается репрезентативным для целого планарного волокнистого мата. В массиве 1D можно выделить три типа волокон: внутренние центральные (с продольной плоскостью симметрии каркаса, разделяющей их пополам), внутренние переходные (с боковой поверхностью, окруженной другими волокнами, но с асимметричными сторонами) и внешняя (на краю каркаса). Пять - это минимальное количество волокон, необходимое для того, чтобы включить все три определенных типа.

Размер элемента сетки модели требует особого внимания, так как он может повлиять на результаты моделирования и, следовательно, не выявить важные эффекты (рисунок 4). Это общее правило метода конечных элементов и следствие теоремы Найквиста-Шеннона о выборке. Чем быстрее основные сигналы моделирования колеблются в пространстве, тем меньше должны быть элементы сетки, чтобы создать лояльное представление явления. С другой стороны, чем меньше элемент, тем больше общее количество строительных блоков модели и вычислительные затраты. Адаптивная очистка сетки, установленная в разделе 2.1, является хорошим и легким методом для уравновешивания этих противоположных целей путем уменьшения размера элемента только там, где и до тех пор, пока эта операция приводит к значительным изменениям.

Слишком упрощенная модель может потерпеть неудачу, представляя важные эффекты(рисунок5,6). Моделирование показывает, что учет морфологии поверхности и электрических свойств компонентов каркаса не является избыточным при прогнозировании электрических микросред. В то время как морфология поверхности оказывает непосредственное влияние на стационарный EF (сравните SC и SNC с RC, RNC и RNCd), сравнение между предсказаниями RC и RNC показывает, что непроводящие волоконные сердечники усиливают этот эффект. С точки зрения моделирования клеточных электрических микросред на нановолокнистых каркасах, модели SC, SNC и RC являются, таким образом, неоптимальными. Тем не менее, хорошей практикой является постепенное добавление сложности, поскольку сравнения между различными этапами помогают указать, какие особенности приводят к конкретным эффектам.

Сложность модели влияет на изменение тока и плотности заряда при выравнивании волокон по EF. Предлагаемый протокол помогает выделить эффект(рисунок 5,6). В то время как модель SC не показывает никаких изменений в предлагаемых метриках при изменении ее выравнивания с градиентом электрического потенциала, моделирование модели RNC предсказывает мощный контраст между матовым блоком с волокнами, выровненными к EF, и блоком с перпендикулярными волокнами(рисунок 7). Когда непроводящие керны ступают на пути течения тока, они образуют периодические плотины, которые приводят к чередованию областей с высокой и низкой плотностью заряда.

Динамические режимы ЭС могут быть смоделированы с помощью зависимых от времени исследований. Видео в дополнительных файлах показывают прогнозы, сделанные для синусоидального входного напряжения на полной модели искусственного каркаса (RNC), с волокнами, параллельными или перпендикулярными градиенту электрического потенциала. Небольшие токи вдоль волокон, перпендикулярных EF, появляются, когда заряд высвобождается из каркаса по мере уменьшения величины EF. Это показывает, что стимуляция может происходить не только при наличии внешнего EF, но и сразу после его отключения - см. дополнительные файлы для видео.

figure-results-6070
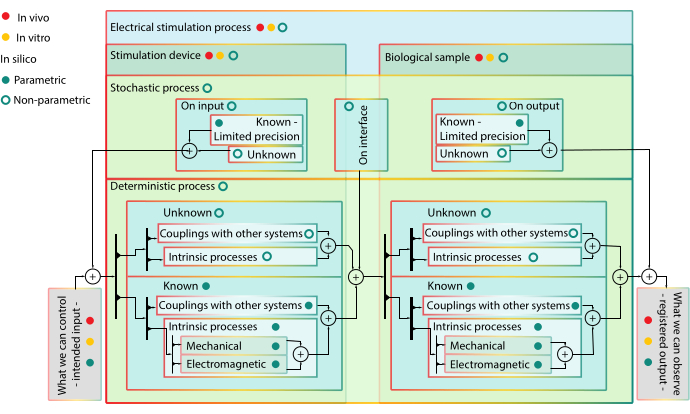
Рисунок 1:Иерархическая блок-схема моделирования - преимущества и ограничения моделирования с моделями in vivo и in silico. Цветом блока помечают блоки на одном иерархическом уровне. Блоки более низкого ранга включаются в блоки более высокого ранга. Цветовые метки обводки блока могут включать блок в определенный тип модели - связь с другими системными блоками не имеет желтого цвета в их обводке, так как они не являются компонентами для моделей in vitro. Пули действуют как клапаны и означают управляемость блока. Когда клапан включен, сигнал может проходить через все стрелковые пути в подчиненных подсистемах, которые имеют цвет клапана в их ходу. Интерпретация диаграммы: процесс ES состоит из стимулирующего устройства и биологической мишени, каждая из которых имеет несколько взаимосвязанных детерминированных или стохастических подпроцессов, которые не могут быть разделены in vivo или in vitro, поэтому они не имеют красного или желтого клапана. Стохастические процессы также вмешиваются на границе между устройством моделирования и биологическим образцом, когда они оба стимулируются. Модель in vitro отделяет интересуящей систему (т.е. сегмент кожи) от остальной части организма. Таким образом, можно наблюдать только внутренние процессы интересующих систем, увенчанные стохастическими процессами различной природы. Однако различные внутренние процессы, связанные с этим, не могут быть стимулированы и идентифицированы отдельно. Модели in silico являются параметрическими для известных компонентов - их поведение, как ожидается, будет определенной формы - и непараметрическим для неизвестного - поскольку нет механистических оснований доверять определенной экстраполяции. Все компоненты in silico могут быть смоделированы отдельно или в разных комбинациях, что позволяет изобразить различные гипотезы. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.

figure-results-8260
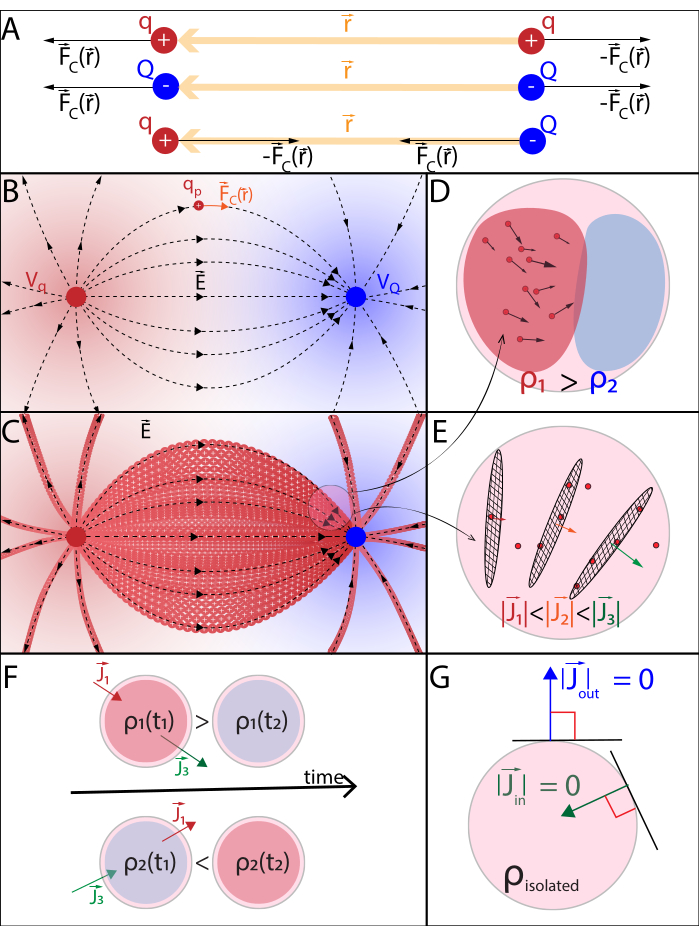
Рисунок 2:(A) Закон Кулона (B) Поле электрического потенциала и заряд подвижного зонда (C) Электрический ток (D) Плотность заряда (E) Плотность тока (F) Уравнение непрерывности (G) Закон сохранения заряда. (A) Электрически заряженные стационарные частицы q и Q взаимодействуют электростатически через силу 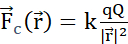figure-results-8728 Кулона. (В1) Каждая заряженная частица Q генерирует скалярное поле, называемое электрическим потенциалом во всех положениях 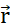figure-results-8966 в пространстве: 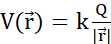figure-results-9078 . Максимальная работа, необходимая для перемещения другой заряженной частицы q из ее 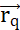figure-results-9260 положения, представляется произведением между зарядом q и электрическим потенциалом, генерируемым Q в 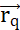figure-results-9458 положении. Электрическое потенциальное поле, генерируемое несколькими частицами, является суммой полей, генерируемых каждой отдельной частицей. (В2) Стационарное поле с неподвижными частицами генератора q и Q, действует с 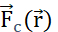figure-results-9793 частицей на зонд с положительным зарядом qp. В ответ qp движется, чтобы минимизировать электрический потенциал своего положения. Чтобы описать движение qp,можно вывести 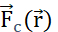figure-results-10092 и электрическое поле 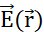figure-results-10210 из электрического потенциального поля: 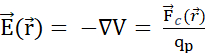figure-results-10346 . (C) Множественные подвижные положительно заряженные частицы зонда, равномерно высвобождаемые в неподвижном электрическом поле, следуют за организованным движением. Чтобы отслеживать конфигурацию заряда, не отслеживая каждую частицу, можно в каждый момент времени указать: (D) как пространство занято частицами, присваивая плотность 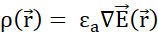figure-results-10811 заряда каждому бесконечно малому объему, согласно закону Гаусса, и (E) как частицы проходят через граничные поверхности между соседними бесконечно малыми объемами, присваивая плотность тока 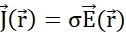figure-results-11115 каждой границе в соответствии с законом Ома. (F) Плотность заряда и тока развиваются в зависимости от уравнения непрерывности, поскольку неравномерное смещение частиц приводит либо к накоплению, либо к потере частиц в определенном объеме. (G) В изолированной системе преобладает закон сохранения заряда, и нет притока или оттока заряженных частиц. Используемые обозначения:- q,Q,qp заряд и название заряженной частицы; 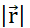figure-results-11693 - евклидова норма вектора положения; k - постоянная Кулона; 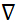figure-results-11851 - оператор градиента, εа - абсолютная диэлектрическая проницаемость среды; σ - проводимость среды. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.

figure-results-12302
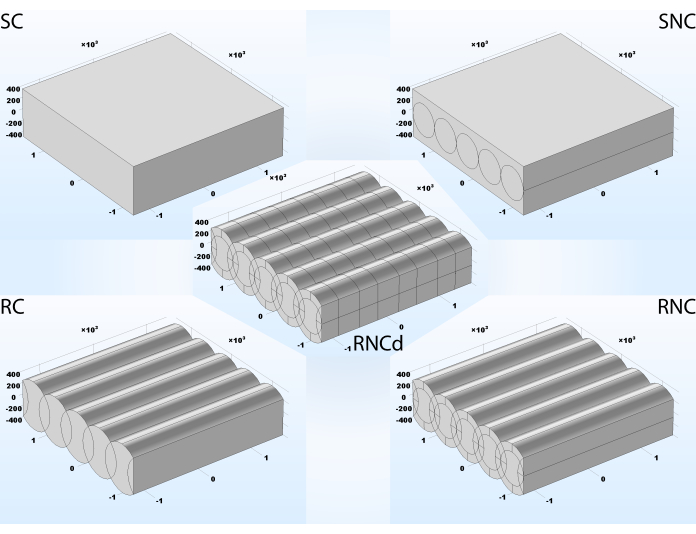
Рисунок 3:Пять различных уровней сложности для волокнистого мата. SC- гладкая с проводящими встроенными волокнами, простейшая модель, не учитывающая морфологию поверхности или различные свойства составляющих компонентов; SNC- гладкие с непроводящими встроенными волокнами; RC- шероховатая с проводящими встроенными волокнами, учитывающая морфологию поверхности, но не различные свойства компонентов; RNC- шероховатая с непроводящими встроенными волокнами, полностью предложенная модель нановолокнистых искусственных лесов; RNCd- грубые с непроводящими встроенными волокнами, покрытыми двумя различными материалами, полностью предлагаемая модель для листа коллагеновых волокон. Используемая единица измерения длины: нанометры. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.

figure-results-13472
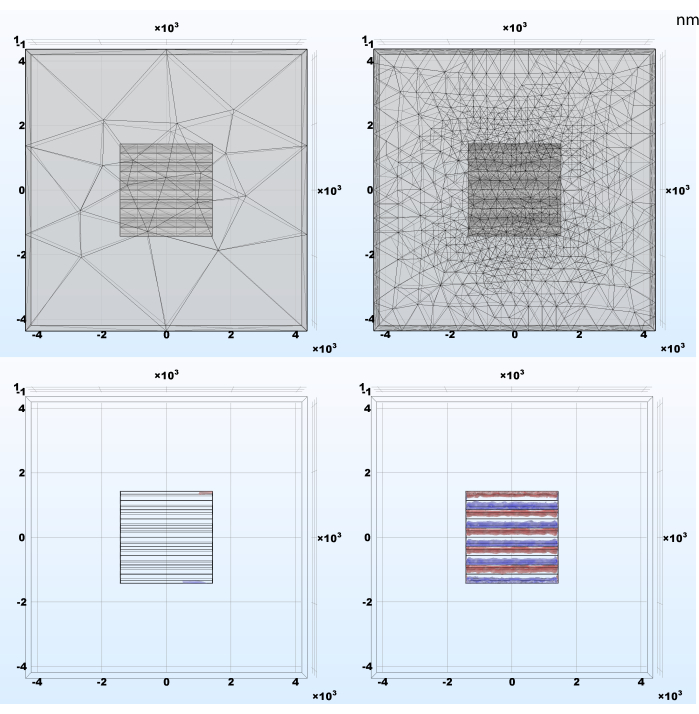
Рисунок 4:Пример результатов адаптивной уточнения сетки и результирующей плотности заряда после моделирования. (Слева) Автоматически генерируемая сетка с экстрагрубыми тетраэдрическими элементами; (Справа) Начальная сетка адаптивно отладелывался при стационарном исследовании; меньшие элементы требуются для точного результата в областях, где моделируемые сигналы имеют резкие пространственные изменения. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.

figure-results-14253
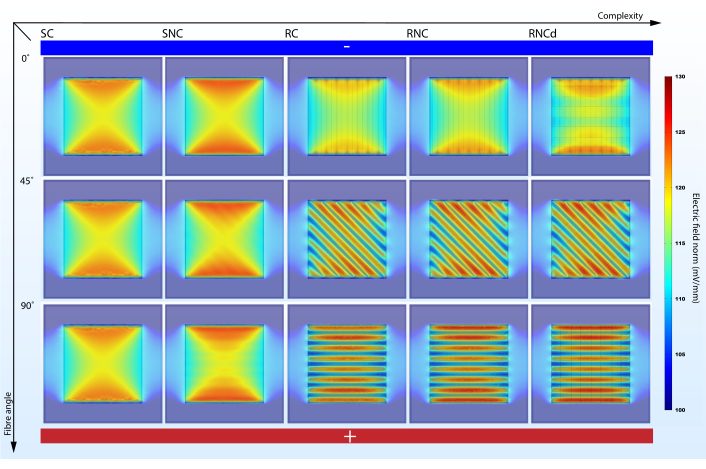
Рисунок 5:Угол выравнивания волокна к электрическому градиенту потенциала влияет на прочность EF в окружающих средах клеточных культур, когда учитывается достаточная сложность. SC, SNC, RC, RNC и RNCd - это различные уровни сложности для модели волокнистого мата, представленной на рисунке 3. Вертикальная ось отмечает угол выравнивания волокон до градиента электрического потенциала. Абстрактные электроды - нижняя сторона с высоким электрическим потенциалом и верхняя сторона с низким электрическим потенциалом. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.

figure-results-15173
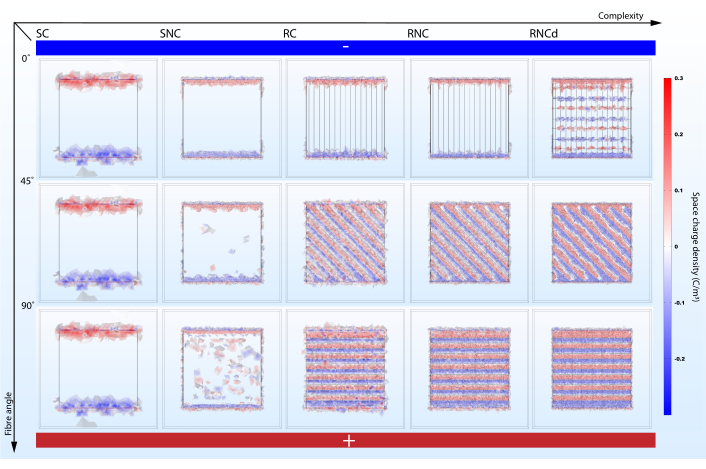
Рисунок 6:Угол выравнивания волокна к электрическому градиенту потенциала влияет на плотность заряда пространства в окружающих средах клеточных культур, когда учитывается достаточная сложность. SC, SNC, RC, RNC и RNCd - это различные уровни сложности для модели волокнистого мата, представленной на рисунке 3. Вертикальная ось отмечает угол выравнивания волокон до градиента электрического потенциала. Абстрактные электроды -нижняя сторона с высоким электрическим потенциалом и верхняя сторона с низким электрическим потенциалом. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.

figure-results-16154
Рисунок 7:На движение заряда влияет выравнивание волокна каркаса относительно EF. Обе панели иллюстрируют прогнозы модели RNC в устойчивом состоянии. С левой стороны волокна параллельны EF, в то время как с правой стороны они перпендикулярны. Объем от светло-красного до синего цвета отмечает плотность заряда, а объем стрелки отмечает ориентацию плотности тока. Цвет стрелок соответствует текущей норме плотности. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.

ИмяВыражениеОписание
Ws10 * Rc * med_ratioШирина строительных лесов
Лс10 * Rc * med_ratioДлина строительных лесов
Хс2 * RfВысота строительных лесов
med_ratio1.5Соотношение среды клеточного культивирования к каркасу
РК278.5[нм]Радиус сердцевины волокна
r1.5Отношение сердечника волокна к покрытию
РфРк*рВолокно с радиусом покрытия
Тета90[ог]Угол ориентации волокна
Если1.3*(Ls*cos(тета)+Ws*sin(тета))Длина волокна
тес1Отношение радиуса сердцевины волокна к расстоянию между волокнами
n_12*(fix((Ws/(2*cos(theta))-Rf)/(2*tes*Rc))+3)*(cos(theta)!=0)+1*(cos(theta)==0)Максимальное количество волокон, если тета<=45
n_22*(fix((Ls/(2*sin(theta))-Rf)/(2*tes*Rc))+3)*(sin(theta)!=0)+1*(sin(theta)==0)Максимальное количество волокон, если тета>45
избыток1,2 + 0,3 * абс (грех (2 * тета))Первое относительное смещение волокна от каркаса
DЛф/5Периодичность шерсти
подпорка0.46Длина первого слоя относительно периодичности D
E100[мВ/мм]Величина электрического поля
В0Е*ЛС*med_ratioНапряжение клеммы
омега500[Гц]Зависящий от времени исследование Частота напряжения
p_sigma0.5Относительная проводимость второго покрытия
p_eps1.5Второе покрытие относительной диэлектрической проницаемоем

Таблица 1: Параметры, используемые для моделирования

Культура МедиаПЕДОТ:ПСС 1ПЕДОТ:ПСС 2Коллаген Гидратированный 1Коллаген Гидратированный 2Фиброин шелкаКоллаген сухой
Электропроводность (С/м)1.70141.00Е-01p_sigma * 0.12.00Е-05p_sigma * 2e-51.00Е-082.50Е-08
Относительная диэлектриктность80.12.2p_eps * 2.29.89p_eps * 9.897.81E+004.97

Таблица 2: Свойства материала, используемые при моделировании

Дополнительные файлы. Пожалуйста, нажмите здесь, чтобы загрузить этот файл.

Обсуждение

Предлагаемый протокол предлагает единообразное решение для моделирования естественных и искусственных каркасов и подчеркивает необходимость учитывать наноструктуру волокнистых каркасов при проверке воздействия EF на клетки, засеянные на такие материалы. Хотя грубое приближение к напряженности EF (разность потенциалов электродов, деленная на расстояние между электродами) привело бы нас к ожиданию напряженности поля 100 мВ/ мм, моделирование предсказывает напряженность стационарного поля до 30% выше в различных областяхмата (рисунок 5). Этот результат должен представлять интерес при разработке эксперимента ЭС и интерпретации данных, так как гибель клеток может быть вызвана слишком сильными ЭФ. Воздействие электрической микросреды позволит напрямую корреляцию между ЭС и клеточным развитием. Хотя в нескольких исследованиях представлен подробный морфологический анализ используемых каркасов33,43,59,они не исследуют взаимодействие между структурой, электрическими свойствами материалов и EF. Этот протокол может включать эту связь, поскольку такие параметры, как радиус волокна, толщина слоя покрытия, расстояние между волокнами и электрические свойства компонентных материалов, могут быть изменены в соответствии с каждым экспериментом путем изменения глобальных определений на этапах 1.2 и 1.3. Следовательно, настраиваемые 3D-прогнозы пространственного разрешения заряда и плотности тока могут быть сделаны как для статических, так и для динамических режимов ES.

Оптимизация конструкции каркаса может быть нацелена на модели RNC и RNCd с широким диапазоном параметров, масштабированием предлагаемых морфологий или их частей. Альтернативно, другие конфигурации каркасов могут быть исследованы с помощью предлагаемого протокола путем изменения типов массивов с линейных на трехмерные в разделе 1.6.5 и адаптации геометрии строительных лесов в разделе 1.6.2. Однако оптимизация строительных лесов не может быть выполнена без цели. В то время как для целей тканевой инженерии основное внимание уделяется судьбе клеток, более четкая картина того, какие стимулы являются ее основными детерминантами, необходима, если желательен ее надежный контроль. Плотность заряда и тока являются хорошими дескрипторами клеточных электрических микросред, поскольку они показывают взаимодействие между EF и электрическими свойствами различных компонентных материалов сложных каркасов, таких как ECM. Протокол показывает, как вычислять прогнозы для этих метрик с учетом геометрии нановолокнистого каркаса, и подчеркивает важность угла выравнивания волокон с EF. Затем предсказания заряда и плотности тока могут быть связаны с клеточным развитием и, таким образом, каркасные и ES-режимы могут быть оптимизированы для конкретных задач.

Интересно, что исследование показывает, что воздействие EF генерировало механическое напряжение более чем в два раза по прочности в композитных пленках с нановолокнами, перпендикулярными внешнему EF, по сравнению с пленками с параллельным выравниванием60. Зарегистрированное механическое напряжение может быть результатом кулоновых сил, действующих между заряженными волокнами, предсказанных грубыми моделями моделирования (RC, RNC, RNCd)(рисунок 6). Хотя эти симуляции могут быть полезны при исследовании этой гипотезы, следует отметить, что сообщенные экспериментальные результаты были получены в системе с емкостной связью, и моделирование представляет собой прямую связь.

Ограничивающим фактором для будущего возможного использования протокола для оценки входного сигнала сотовой связи является неопределенность параметров. Геометрическими неопределенными параметрами являются толщина слоя покрытия и расстояние между сердечниками волокна. Первый можно вывести, найдя значение, которое приводит к объему импеданса, которое может быть экспериментально проверено. Второй может быть извлечен из сканирования материалов высокого разрешения. Параметры, описывающие физические свойства материалов, также подвержены влиянию неопределенности. Однако электропроводность и диэлектрическая проницаемость образцовых материалов отличаются гораздо больше, чем экспериментальная точность измерения(таблица 2). Таким образом, сообщаемые эффекты будут сохранены, несмотря на умеренные погрешности измерений.

Результаты показывают, как недостаток сложности модели может скрывать соответствующую информацию. Важно признать, что протокол имитирует упрощенную версию происходящего физического явления, поскольку он не учитывает различную природу материалов, участвующих в процессе - проводник (электроды), полупроводник (покрытие), диэлектрик (волоконные сердечники) и электролитический (окружающее вещество) - которые способны влиять на перенос заряда. Эта проблема может быть учтена в будущих расширениях модели путем добавления задержек передачи энергии на границах раздела (т.е. реакций Фарада) и задержек переноса ионов внутри электролита. Однако добавление сложности должно основываться на экспериментальной проверке, поскольку простая модель, которая воспроизводит большую часть наблюдаемого, более полезна, чем удивительно точная, которая добавляет немного больше информации, но глубоко чувствительна к неопределенности многих составляющих параметров.

Поскольку конечной целью тканевой инженерии является создание биореакторов, которые не только имитируют один или два аспекта сред in vivo, но и реплицируют и контролируют все клеточные сигналы развития61,электромагнитные и механические модели in silico, а также модели теплопередачи между компонентами биореактора должны быть объединены. На последующей фазе моделирования также могут быть добавлены явления связи между этими взаимодействиями, такие как омический нагрев, поток электролитической жидкости, морфологические деформации каркаса в ответ на электрическую стимуляцию60 и пьезоэлектричество62. Однако модели следует объединять только после того, как каждая из них была экспериментально проверена. Таким образом, мы можем лучше понять влияние каждого компонента в клеточной микросреде и то, как стимулы могут быть оптимизированы.

Если предложенная модель экспериментально валидирована, ее можно комбинировать с моделями биологических клеток - рисунок 1. Паттерны плотности заряда и модуляции могут асимметрично влиять на активность специфических ионных насосов, влиять на присоединение к волокну белков, управляя адгезией мембраны63 и, следовательно, направлять миграцию, паттерны пролиферации и морфогенез64. Изучение этих гипотез является путем вперед в понимании механизмов, лежащих в основе тканевых и клеточных реакций на ЭС.

Раскрытие информации

Авторам нечего раскрывать.

Благодарности

Эта работа была поддержана 4-летней программой Wellcome Trust PhD в области количественной и биофизической биологии.

Материалы

NameCompanyCatalog NumberComments
Comsol multiphysics 5.2 AC/DC moduleCOMSOL-FEM modelling software

Ссылки

  1. Zhao, S., Mehta, A. S., Zhao, M. Biomedical applications of electrical stimulation. Cellular and Molecular Life Sciences. 77 (14), 2681-2699 (2020).
  2. Gordon, T. Electrical Stimulation to Enhance Axon Regeneration After Peripheral Nerve Injuries in Animal Models and Humans. Neurotherapeutics. 13 (2), 295-310 (2016).
  3. Pedrotty, D. M., et al. Engineering skeletal myoblasts: Roles of three-dimensional culture and electrical stimulation. American Journal of Physiology - Heart and Circulatory Physiology. 288, 1620-1626 (2005).
  4. Stoppel, W. L., Kaplan, D. L., Black, L. D. Electrical and mechanical stimulation of cardiac cells and tissue constructs. Advanced Drug Delivery Reviews. 96, 135-155 (2016).
  5. Leppik, L., et al. Combining electrical stimulation and tissue engineering to treat large bone defects in a rat model. Scientific Reports. 8 (1), (2018).
  6. Du, S., et al. Bioinspired hybrid patches with self-adhesive hydrogel and piezoelectric nanogenerator for promoting skin wound healing. Nano Research. 13 (9), 2525-2533 (2020).
  7. Gratieri, T., Santer, V., Kalia, Y. N. Basic principles and current status of transcorneal and transscleral iontophoresis. Expert Opinion on Drug Delivery. 14 (9), 1091-1102 (2017).
  8. Kroeling, P., Gross, A., et al. Electrotherapy for neck pain. Cochrane Database of Systematic Reviews. 2013 (8), (2013).
  9. Hurlow, A., et al. Transcutaneous electric nerve stimulation (TENS) for cancer pain in adults. Cochrane Database of Systematic Reviews. 2012 (3), (2012).
  10. Claydon, L. S., Chesterton, L. S., Barlas, P., Sim, J. Dose-specific effects of transcutaneous electrical nerve stimulation (TENS) on experimental pain: A systematic review. Clinical Journal of Pain. 27 (7), 635-647 (2011).
  11. Sbruzzi, G., Silveira, S. A., Silva, D. V., Coronel, C. C., Plentz, R. D. M. Estimulação elétrica nervosa transcutânea no pós-operatório de cirurgia torácica: Revisão sistemática e metanálise de estudos randomizados. Brazilian Journal of Cardiovascular Surgery. 27 (1), 75-87 (2012).
  12. Jin, D. M., Xu, Y., Geng, D. F., Yan, T. b. Effect of transcutaneous electrical nerve stimulation on symptomatic diabetic peripheral neuropathy: A meta-analysis of randomized controlled trials. Diabetes Research and Clinical Practice. 89 (1), 10-15 (2010).
  13. Bjordal, J. M., et al. Short-term efficacy of physical interventions in osteoarthritic knee pain. A systematic review and meta-analysis of randomised placebo-controlled trials. BMC Musculoskeletal Disorders. 8 (1), 51 (2007).
  14. Johnson, M., Martinson, M. Efficacy of electrical nerve stimulation for chronic musculoskeletal pain: A meta-analysis of randomized controlled trials. Pain. 130 (1-2), 157-165 (2007).
  15. Johnson, M. I. Transcutaneous Electrical Nerve Stimulation (TENS). eLS. , 1-13 (2012).
  16. Griffin, M., Bayat, A. Electrical stimulation in bone healing: critical analysis by evaluating levels of evidence. Eplasty. 11, (2011).
  17. Mollon, B., Da Silva, V., Busse, J. W., Einhorn, T. A., Bhandari, M. Electrical stimulation for long-bone fracture-healing: A meta-analysis of randomized controlled trials. Journal of Bone and Joint Surgery - Series A. 90 (11), 2322-2330 (2008).
  18. Eberstein, A., Eberstein, S. Electrical stimulation of denervated muscle: Is it worthwhile. Medicine and Science in Sports and Exercise. 28 (12), 1463-1469 (1996).
  19. Mödlin, M., et al. Electrical stimulation of denervated muscles: First results of a clinical study. Artificial Organs. 29 (3), 203-206 (2005).
  20. Gordon, T., Amirjani, N., Edwards, D. C., Chan, K. M. Brief post-surgical electrical stimulation accelerates axon regeneration and muscle reinnervation without affecting the functional measures in carpal tunnel syndrome patients. Experimental Neurology. 223 (1), 192-202 (2010).
  21. Chan, K. M., Curran, M. W. T., Gordon, T. The use of brief post-surgical low frequency electrical stimulation to enhance nerve regeneration in clinical practice. Journal of Physiology. 594 (13), 3553-3559 (2016).
  22. Vance, C. G. T., Dailey, D. L., Rakel, B. A., Sluka, K. A. Using TENS for pain control: the state of the evidence. Pain management. 4 (3), 197-209 (2014).
  23. Peters, E. J., Lavery, L. A., Armstrong, D. G., Fleischli, J. G. Electric stimulation as an adjunct to heal diabetic foot ulcers: A randomized clinical trial. Archives of Physical Medicine and Rehabilitation. 82 (6), 721-725 (2001).
  24. Lundeberg, T. C. M., Eriksson, S. V., Malm, M. Electrical nerve stimulation improves healing of diabetic ulcers. Annals of Plastic Surgery. 29 (4), 328-331 (1992).
  25. Houghton, P. E., et al. Electrical Stimulation Therapy Increases Rate of Healing of Pressure Ulcers in Community-Dwelling People With Spinal Cord Injury. Archives of Physical Medicine and Rehabilitation. 91 (5), 669-678 (2010).
  26. Bikbova, G., Bikbov, M. Standard corneal collagen crosslinking versus transepithelial iontophoresis-assisted corneal crosslinking, 24 months follow-up: randomized control trial. Acta Ophthalmologica. 94 (7), 600-606 (2016).
  27. Bhavsar, M. B., et al. Electrical stimulation-based bone fracture treatment, if it works so well why do not more surgeons use it. European Journal of Trauma and Emergency Surgery. 46 (2), 245-264 (2020).
  28. Erickson, C. A., Nuccitelli, R. Embryonic fibroblast motility and orientation can be influenced by physiological electric fields. Journal of Cell Biology. 98 (1), (1984).
  29. Hammerick, K. E., Longaker, M. T., Prinz, F. B. In vitro effects of direct current electric fields on adipose-derived stromal cells. Biochemical and Biophysical Research Communications. 397 (1), 12-17 (2010).
  30. Shao, S., et al. Osteoblast function on electrically conductive electrospun PLA/MWCNTs nanofibers. Biomaterials. 32 (11), 2821-2833 (2011).
  31. Forciniti, L., Ybarra Iii, J., Zaman, M. H., Schmidt, C. E. Schwann cell response on polypyrrole substrates upon electrical stimulation. Acta Biomaterialia. , (2014).
  32. Kumar, A., Nune, K. C., Misra, R. D. K. Electric field-mediated growth of osteoblasts-the significant impact of dynamic flow of medium. Biomaterials Science. 4 (1), 136-144 (2016).
  33. Hyun Ko, U., et al. Promotion of Myogenic Maturation by Timely Application of Electric Field Along the Topographical Alignment. Tissue Engineering Part A. 24 (10), 752-760 (2018).
  34. Lynch, K., Skalli, O., Sabri, F. Growing Neural PC-12 Cell on Crosslinked Silica Aerogels Increases Neurite Extension in the Presence of an Electric Field. Journal of Functional Biomaterials. 9 (2), 30 (2018).
  35. Balint, R., Cassidy, N. J., Cartmell, S. H. Electrical stimulation: A novel tool for tissue engineering. Tissue Engineering - Part B: Reviews. 19 (1), 48-57 (2013).
  36. Chen, C., Bai, X., Ding, Y., Lee, I. S. Electrical stimulation as a novel tool for regulating cell behavior in tissue engineering. Biomaterials Research. 23 (1), (2019).
  37. Purushothaman, A. E., Thakur, K., Kandasubramanian, B. Development of highly porous, Electrostatic force assisted nanofiber fabrication for biological applications. International Journal of Polymeric Materials and Polymeric Biomaterials. 69 (8), 477-504 (2020).
  38. Yanılmaz, M., Sarac, A. S. A review: Effect of conductive polymers on the conductivities of electrospun mats. Textile Research Journal. 84 (12), 1325-1342 (2014).
  39. Tsukada, S., Nakashima, H., Torimitsu, K. Conductive polymer combined silk fiber bundle for bioelectrical signal recording. PLoS ONE. 7 (4), 33689 (2012).
  40. Nguyen, H. T., et al. Electric field stimulation through a biodegradable polypyrrole-co- polycaprolactone substrate enhances neural cell growth. Journal of Biomedical Materials Research - Part A. 102 (8), 2554-2564 (2014).
  41. Song, J., et al. Polymerizing pyrrole coated poly (l-lactic acid-co-ε-caprolactone) (PLCL) conductive nanofibrous conduit combined with electric stimulation for long-range peripheral nerve regeneration. Frontiers in Molecular Neuroscience. 9, (2016).
  42. Lee, J. Y., Bashur, C. A., Goldstein, A. S., Schmidt, C. E. Polypyrrole-coated electrospun PLGA nanofibers for neural tissue applications. Biomaterials. 30 (26), 4325-4335 (2009).
  43. Du, L., et al. Combined effects of electrospun nanofibrous scaffold and electrical field on the neuronal outgrowth. Materials Letters. 256, (2019).
  44. Theocharis, A. D., Skandalis, S. S., Gialeli, C., Karamanos, N. K. Extracellular matrix structure. Advanced Drug Delivery Reviews. 97, 4-27 (2016).
  45. Shoulders, M. D., Raines, R. T. Collagen structure and stability. Annual Review of Biochemistry. 78, 929-958 (2009).
  46. Fang, M., et al. Type i collagen D-spacing in fibril bundles of dermis, tendon, and bone: Bridging between nano- and micro-level tissue hierarchy. ACS Nano. 6 (11), 9503-9514 (2012).
  47. PETRUSKA, J. A., HODGE, A. J. a Subunit Model for the Tropocollagen Macromolecule. Proceedings of the National Academy of Sciences of the United States ofAmerica. 51 (5), 871-876 (1964).
  48. Kastelic, J., Galeski, A., Baer, E. The multicomposite structure of tendon. Connective Tissue Research. 6 (1), 11-23 (1978).
  49. Thorpe, C. T., Birch, H. L., Clegg, P. D., Screen, H. R. C. The role of the non-collagenous matrix in tendon function. International Journal of Experimental Pathology. 94 (4), 248-259 (2013).
  50. Chapman, G. E., McLauchlan, K. A. The hydration structure of collagen. Proceedings of the Royal Society of London. Series B. Biological Sciences. 173 (31), 223-234 (1969).
  51. Bardelmeyer, G. H. Electrical conduction in hydrated collagen. I. Conductivity mechanisms. Biopolymers. 12 (10), 2289-2302 (1973).
  52. Budde, K., et al. Requirements for Documenting Electrical Cell Stimulation Experiments for Replicability and Numerical Modeling. Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society. , 1082-1088 (2019).
  53. Zhao, S., Mehta, A. S., Zhao, M. Biomedical applications of electrical stimulation. Cellular and Molecular Life Sciences. 77 (14), 2681-2699 (2020).
  54. Zhang, T., Yi, Y. B. Monte Carlo simulations of effective electrical conductivity in short-fiber composites. Journal of Applied Physics. 103 (1), 14910 (2008).
  55. Meny, I., Burais, N., Buret, F., Nicolas, L. Finite element modeling of cell exposed to harmonic and transient electric fields. 12th Biennial IEEE Conference on Electromagnetic Field Computation, CEFC 2006. 43 (4), 310 (2006).
  56. Schoenbach, K. H., et al. Ultrashort electrical pulses open a new gateway into biological cells. Proceedings of the IEEE. 92 (7), 1122-1136 (2004).
  57. Gowrishankar, T. R., Smith, K. C., Weaver, J. C. Transport-based biophysical system models of cells for quantitatively describing responses to electric fields. Proceedings of the IEEE. 101 (2), 505-517 (2013).
  58. Pietak, A., Levin, M. Exploring instructive physiological signaling with the bioelectric tissue simulation engine. Frontiers in Bioengineering and Biotechnology. 4, (2016).
  59. Babaie, A., et al. Synergistic effects of conductive PVA/PEDOT electrospun scaffolds and electrical stimulation for more effective neural tissue engineering. European Polymer Journal. 140, 110051 (2020).
  60. Zhou, J., Fukawa, T., Kimura, M. Directional electromechanical properties of PEDOT/PSS films containing aligned electrospun nanofibers. Polymer Journal. 43 (10), 849-854 (2011).
  61. Castro, N., et al. Physically Active Bioreactors for Tissue Engineering Applications. Advanced Biosystems. 4 (10), 1-29 (2020).
  62. Ribeiro, S., Gomes, A. C., Etxebarria, I., Lanceros-Méndez, S., Ribeiro, C. Electroactive biomaterial surface engineering effects on muscle cells differentiation. Materials Science and Engineering. , (2018).
  63. Marzocchi, M., et al. Physical and Electrochemical Properties of PEDOT:PSS as a Tool for Controlling Cell Growth. ACS Applied Materials and Interfaces. 7 (32), 17993-18003 (2015).
  64. Leronni, A., Bardella, L., Dorfmann, L., Pietak, A., Levin, M. On the coupling of mechanics with bioelectricity and its role in morphogenesis. Journal of the Royal Society Interface. 17 (167), 20200177 (2020).

Перепечатки и разрешения

Запросить разрешение на использование текста или рисунков этого JoVE статьи

Запросить разрешение

Смотреть дополнительные статьи

171

This article has been published

Video Coming Soon

JoVE Logo

Конфиденциальность

Условия эксплуатации

Политика

СВЯЖИТЕСЬ С НАМИ

РЕКОМЕНДОВАТЬ БИБЛИОТЕКЕ

НОВОСТИ JoVE

Исследования

Образование

АВТОРЫ

Библиотекарь

О JoVE

Авторские права © 2025 MyJoVE Corporation. Все права защищены