ARL Spectral Fitting als Anwendung zur Erweiterung von Spektraldaten mittels Franck-Condon-Linienformanalyse und Farbanalyse

Zusammenfassung

Dieses Protokoll führt Franck-Condon Lineshape Analyses (FCLSA) von Emissionsspektren ein und dient als Tutorial für die Verwendung der ARL Spectral Fitting Software. Die Open-Source-Software bietet eine einfache und intuitive Möglichkeit, erweiterte Analysen von Emissionsspektren durchzuführen, einschließlich Energieberechnungen im angeregten Zustand, CIE-Farbkoordinatenbestimmung und FCLSA.

Zusammenfassung

Die Anwendung ARL Spectral Fitting bietet eine kostenlose, öffentlich zugängliche und vollständig transparente Methode zur Durchführung der Franck-Condon-Linienformanalyse (FCLSA) für Spektraldaten, zusätzlich zur CIE-Farbkoordinatenbestimmung und grundlegenden spektralen Verarbeitung. Während einige der Funktionen in kommerzieller Software oder in Programmen akademischer Forschungsgruppen zu finden sind, glauben wir, dass ARL Spectral Fitting die einzige Anwendung ist, die alle drei oben genannten Attribute besitzt.

Dieses Programm ist als eigenständige, GUI-basierte Anwendung für einen durchschnittlichen Laborforscher gedacht, ohne dass Programmierkenntnisse oder proprietäre Software erforderlich sind. Zusätzlich zu der eigenständigen ausführbaren Datei, die auf ARL GitHub gehostet wird, stehen die zugehörigen MATLAB-Dateien zur Verwendung und Weiterentwicklung zur Verfügung.

FCLSA erweitert die in Lumineszenzspektren gefundenen Informationen und liefert aussagekräftige Einblicke in die Beziehung zwischen dem Boden und angeregten Zuständen einer photolumineszierenden Spezies. Diese Erkenntnis wird erreicht, indem Spektren mit zwei Versionen (Moden) einer Gleichung modelliert werden, die entweder durch vier oder sechs Parameter gekennzeichnet sind, je nachdem, welcher Modus verwendet wird. Nach der Optimierung kann der Wert jedes dieser Parameter verwendet werden, um Einblicke in das Molekül zu gewinnen und weitere Analysen durchzuführen (z. B. den freien Energiegehalt des Moleküls im angeregten Zustand). Diese Anwendung bietet Werkzeuge für die einfache manuelle Anpassung importierter Daten sowie zwei Methoden zur Optimierung dieser passgenauen Anpassung der kleinsten Quadrate, die auf dem Levenberg-Marquardt-Algorithmus basiert, und die ableitungsfreie Anpassung unter Verwendung des Nelder-Mead-Simplex-Algorithmus. Darüber hinaus können Schätzungen der Probenfarbe durchgeführt und in CIE- und RGB-Koordinaten gemeldet werden.

Einleitung

Photolumineszenzmessungen, die sowohl Fluoreszenz- als auch Phosphoreszenzspektren umfassen, sind in verschiedenen akademischen Bereichen und industriellen Anwendungen weit verbreitet¹. Photokatalysatoren werden zunehmend in der organischen Synthese zur Herstellung komplexer und wertvoller Zielmoleküle ^2,3,4 eingesetzt. Um die Energetik von Photokatalysatoren zu bestimmen, wird die Energie des angeregten Zustands routinemäßig anhand von Emissionsspektren geschätzt. Die Entwicklung neuartiger Beleuchtungsmaterialien, wie z.B. organische Leuchtdioden (OLED) Luminophore, erfordert, dass die beobachtete Farbausgabe charakterisiert und berichtet wird ^5,6. Zu diesem Zweck werden routinemäßig Farbkoordinaten der Commission international de l'éclairage (CIE) verwendet⁷.

Der Zweck der ARL Spectral Fitting-Anwendung besteht darin, eine schnelle und einfache Methode zur Anreicherung von Spektraldaten durch aussagekräftige Analysen bereitzustellen, die sowohl in Bezug auf Benutzerfreundlichkeit als auch auf Verfügbarkeit (https://github.com/USArmyResearchLab/ARL_Spectral_Fitting) allgemein zugänglich sind. Diese Software führt mehrere routinemäßige spektrale Verarbeitungsfunktionen automatisch für den Benutzer aus, einschließlich Datennormalisierung und -konvertierung zwischen Wellenlänge, λ und Wellenzahl, Einheiten mit entsprechender Intensitätsskalierung, 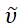wie in der Gleichung unter¹ gezeigt. Die Software ist in der Lage, eine Vielzahl von Eingabe- und Ausgabedateiformaten zu verarbeiten. Mehrere erweiterte Analysen werden einfach mit der Software durchgeführt, wie die Berechnung von CIE- und Chromatizitätskoordinaten, Farbvorhersage, Bestimmung der angeregten freien Energie (ΔG_ES) in verschiedenen Einheiten und FCLSA zur Bestimmung der FCLSA-Parameter⁸.

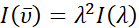
Eine auf grafischer Benutzeroberfläche (GUI) basierende Anwendung wurde verfolgt, da sie es jedem Forscher ermöglicht, diese Analyse durchzuführen und keine Hintergrundkenntnisse der Informatik erfordert. Diese Anwendung wurde in MATLAB mit dem App Designer-Tool geschrieben. Außerhalb von ARL Spectral Fitting ist es praktisch unmöglich, eine öffentlich zugängliche Implementierung einer Anwendung zur Durchführung der Franck-Condon-Linienformanalyse zu finden. Dies liegt daran, dass Forschungsgruppen ihre Implementierungen nicht öffentlich veröffentlichen, sondern es vorziehen, sie proprietär zu halten.

Die Franck-Condon-Linienformanalyse (FCLSA) wird häufig bei der photophysikalischen Charakterisierung neuartiger Verbindungen verwendet, da sie reichhaltige Informationen über das Molekül 9,10,11,12,13,14 vermittelt. Jeder der vier Parameter (sechs im Doppelmodus) gibt Auskunft über den angeregten Zustand des Moleküls. Die Energiegröße oder 0-0 Energielücke (_E0) ist die Differenz zwischen nullten Energieniveaus des Bodens und angeregten Zuständen des Moleküls. Die volle Breite bei halbem Maximum (Δv_1/2)  informiert über die Breiten einzelner vibronischer Linien. Die Elektron-Schwingungs-Kopplungskonstante oder Huang-Rhys-Faktor (S) ist eine dimensionslose Berechnung, die auf der Gleichgewichtsverschiebung zwischen Grund- und angeregten Zuständen des Moleküls¹⁵ basiert. Schließlich ist der Quantenabstandsparameter (ħω) der Abstand zwischen Schwingungsmoden, die den nichtstrahlenden Zerfall eines Moleküls steuern.

Die Gleichungen für Single- und Doublemode-FCLSA lauten wie folgt:

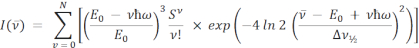
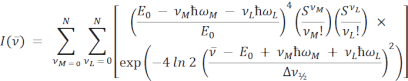
wobei die Parameter wie zuvor definiert sind. In der Doppelmodusgleichung werden S und ħω in mittlere (_M) und niedrige (_L) Energieterme getrennt. 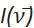ist die Intensität bei der Wellenzahl v^10,16,17,18. In beiden Gleichungen wird die Summierung über N Quantenebenen mit einem Standardwert von N = 5 durchgeführt, wie es in der Literatur¹¹ üblich ist, aber jede ganze Zahl kann in der ARL Spectral Fitting Software unter Settings | Passend.

Protokoll

1. Datenimport

1. Um Daten zu importieren, klicken Sie auf die Schaltfläche Daten importieren . Wählen Sie den Typ des zu importierenden Spektrums aus - entweder Anregung oder Emission.
   1. Sobald ein Spektrumtyp ausgewählt wurde, stellen Sie sicher, dass der MATLAB-Datei-Explorer angezeigt wird. Wählen Sie in diesem Fenster die gewünschte Datei aus und klicken Sie auf Öffnen. Zu den unterstützten Dateitypen gehören .TXT, . CSV, .XLS und . .XLSX.
      HINWEIS: Ein Teil der Datenverarbeitung wird automatisch durchgeführt, bevor die importierten Daten gezeichnet werden. Dazu gehören: Detektion von x-Achseneinheiten (Wellenzahl oder Wellenlänge) und gegebenenfalls Umwandlung in Wellenzahl; Intensitätsnormalisierung des höchsten Peaks auf 1; Berechnung der Energiemenge, falls zutreffend; und Abschätzung des Quantenabstands. Diese Werte werden basierend auf detektierten Datenpeaks berechnet, wobei die Energiemenge dem Wellenzahlwert des höchsten Energiepeaks zugeordnet ist, und der Quantenabstand basierend auf dem gemittelten Abstand zwischen den vicinalen Peaks, was die Detektion von mindestens zwei Peaks erfordert.
2. Um eines der vorgefertigten Probenspektren zu laden, drücken Sie die Taste, die dem gewünschten Spektrum entspricht, das Sie unter Info | Beispielspektren. Neun Probenspektren werden mit der Anwendung vorverpackt.
3. Um mehr als ein Spektrum gleichzeitig zu laden und zu plotten, aktivieren Sie das Kontrollkästchen Mehrere Datenspektren auf Achsen zulassen unter Einstellungen | Allgemeine | Abbildungseinstellungen.
4. Um ein anderes geladenes Spektrum als derzeit aktiv auszuwählen, drücken Sie die Taste " Zu passendes Spektrum auswählen" und wählen Sie dann das gewünschte Spektrum aus der Liste aus, die im neu sichtbaren Bedienfeld " Spektrum auswählen" angezeigt wird.

2. Datenverarbeitung

HINWEIS: Der Benutzer möchte möglicherweise die Datenverarbeitung vor dem Anpassungsprozess durchführen. Zu den verfügbaren Prozessen gehören:

1. Auswahl eines Peaks als Grundlage für die Normalisierung: Um einen Peak auszuwählen, der als Grundlage für die Intensitätsnormalisierung dienen soll, klicken Sie auf die Schaltfläche Select peak for normalization (Spitzenwert für Normalisierung auswählen ) unter Einstellungen | Allgemein. Folgen Sie den Anweisungen auf dem Bildschirm. Der Standardpeak für die Intensitätsnormalisierung ist der höchste Intensitätspeak, der während des Imports gefunden wird.
2. Umrechnung zwischen x-Achseneinheiten: Um die Einheiten der x-Achse zwischen Wellenzahl (^cm-1) und Wellenlänge (nm) umzurechnen, schalten Sie den Schieberegler unter Einstellungen | X-Achse zum gewünschten Modus (entweder Wellenzahl oder Wellenlänge). Sowohl die Intensität als auch die x-Achsen-Einheiten werden für alle belasteten Spektren unter Verwendung der oben angegebenen Gleichung angepasst.
3. Einschränkung des X-Achsenbereichs: Um den X-Achsenbereich manuell einzuschränken, wählen Sie unter Einstellungen |die Option X-Achse manuell anpassen und Grenzwerte anpassen aus. X-Achse. Verwenden Sie dann die angezeigten Steuerelemente, um den x-Achsenbereich anzugeben. Standardmäßig erweitert und verkleinert die Anwendung automatisch den x-Achsenbereich, um alle geladenen Datenpunkte unterzubringen.
4. Alternative E₀ Berechnungsmethoden: Um eine alternative Berechnungsmethode für die Energiemenge auszuwählen, wählen Sie die gewünschte Methode unter Einstellungen | Passend. Die Standardmethode ist Vollständige FCLSA-Anpassung. Um zu einer anderen Methode zu wechseln, wählen Sie die entsprechende radiale Taste und folgen Sie den Anweisungen auf dem Bildschirm¹⁹.

3. Manuelle Montage

HINWEIS: Basierend auf der Menge der im Spektrum sichtbaren Struktur kann es sehr vorteilhaft sein, die Anpassungsparameter vor der Optimierung mit geeigneten Schätzungen zu initialisieren. Diese Initialisierung kann die für die Optimierung erforderliche Zeit verringern und dazu beitragen, dass die von der Optimierung zurückgegebenen Werte für das Spektrum realistisch sind.

1. Zeichnen Sie die Fit-Funktion mit ihren aktuellen Parameterwerten, indem Sie die Schaltfläche Plot-Fit-Funktion drücken.
2. Verwenden Sie eine Kombination aus den Schaltflächen für die Grob- und Feineinstellung, den Schiebereglern und den Bearbeitungsfeldern, um die Parameterwerte anzupassen, um die Anpassungsgüte für geladene Daten zu erhöhen. Standardmäßig wird der Bestimmtheitskoeffizient (R²) in der oberen linken Ecke des Diagramms angezeigt. Verwenden Sie dies als quantitatives Maß für die Anpassungsgüte, um die Auswahl der Parameterwerte zu leiten.
   HINWEIS: Da die Energiegröße (E₀) und der Quantenabstand (ħω) beim Datenimport von der Anwendung berechnet werden, wird empfohlen, diese Werte bei der manuellen Anpassung konstant zu halten oder minimal zu variieren.
3. Standardmäßig verwendet diese Anwendung die Singlemode-Franck-Condon-Linienformanalyseformel, da sie für Raumtemperaturspektren am relevantesten ist. Falls gewünscht, z. B. bei der Anpassung von 77-K-Spektren, wechseln Sie zwischen dem Einzel- und Doppelmodus in den Einstellungen | Passend.
   HINWEIS: Die Überparametrierung wird aufgrund der erhöhten Anzahl von frei schwebenden Parameterwerten zu einem größeren Problem, wenn sie im Doppelmodus im Gegensatz zum Einzelmodus angepasst wird. Breite, strukturlose Emissionsspektren stellen das größte Problem für die Anpassungsalgorithmen dar und können zu einer Kreuzkorrelation zwischen FCLSA-Parametern führen, insbesondere zwischen Δv_1/2 und S. Bei der Anpassung von Spektren ist es unerlässlich, dass die erhaltenen FCLSA-Parameter anhand der Literaturrangfolge als Leitfaden physikalisch realistisch verifiziert werden.

4. Optimierung

1. Nachdem zufriedenstellende Ausgangsparameter gefunden wurden, können weitere Optimierungen durchgeführt werden. Drücken Sie dazu die blaue Taste Optimize Fit . Die Optimierung wird ausgeführt und die Anpassungsfunktion mit neu optimierten Parameterwerten neu dargestellt.
2. Es stehen zwei Optimierungsoptionen zur Verfügung: die Methode der kleinsten Quadrate und die Simplex-Methode. Um zwischen diesen beiden Methoden zu wechseln, wechseln Sie unter Einstellungen | Optimierung zur gewünschten Methode.
3. Passen Sie die Optimierungsmethode bei Bedarf mithilfe der Einstellungen unter Einstellungen | Optimierung an.
   HINWEIS: Um dem Benutzer die Kontrolle über die Optimierungsroutinen zu geben, sind für beide Optimierungsmethoden folgende Anpassungsoptionen möglich:
   1. Werte eines Parameters korrigieren: Um den Wert eines Parameters während der Optimierung zu korrigieren, aktivieren Sie das Kontrollkästchen im Eingabefeld, das dem gewünschten Parameter entspricht.
   2. Benutzerdefinierte Begrenzung eines Parameters während der Optimierung: Um die benutzerdefinierten Begrenzungsoptionen anzuzeigen, aktivieren Sie das Kontrollkästchen Benutzerdefinierte Parameterbegrenzung während der Optimierung zulassen in Einstellungen | Optimierung. Um benutzerdefinierte Grenzen für den Wert eines Parameters während der Optimierung anzugeben, verwenden Sie die Steuerelemente, die durch Klicken auf die Schaltfläche Benutzerdefinierte Grenzen unter dem Bearbeitungsfeld angezeigt werden, das dem gewünschten Parameter entspricht.
   3. Benutzerdefinierte Endtrigger für die Optimierung: Um die maximale Anzahl von Iterationen, die Terminierungstoleranz für den Modellwert oder die Abschlusstoleranz für Koeffizientenwerte anzupassen, aktivieren Sie das entsprechende Kontrollkästchen unter Einstellungen | Optimierung und geben Sie den gewünschten Wert in das entsprechende Eingabefeld ein.
      HINWEIS: Die folgenden Anpassungen sind nur für die Least-Squares-Optimierung verfügbar:
   4. Gütestatistik: Aktivieren Sie das Kontrollkästchen unter Einstellungen | Optimierung anzeigen, um Statistiken zur Anpassungsgüte anzuzeigen (angepasster Bestimmtheitskoeffizient des Freiheitsgrades, Summe der Quadrate aufgrund von Fehlern, Freiheitsgrade im Fehler und quadratischer Fehlermittelwert).
   5. Optionen für robuste Passform: Um die Optionen für die robuste Passform zu aktivieren, wählen Sie das gewünschte Menü aus der Dropdown-Liste unter Einstellungen | Optimierung aus. Standardmäßig ist diese Option deaktiviert. Aktivieren Sie bei Bedarf die Anpassung "Least Absolute Residual Weights" oder "Bisquare Weights", wodurch Ausreißerdatenpunkte weniger Gewicht erhalten.
   6. Gewichtung der Schwellenwertdaten: Um Datenpunkte vorzugsweise über einer Schwellenwertintensität zu gewichten, wählen Sie eine Intensität, die als Schwellenwert fungiert, und einen Gewichtungsmultiplikator, der auf alle Punkte oberhalb dieses Schwellenwerts angewendet wird. Standardmäßig ist diese Option auf on gesetzt, und Schwellenwert und Gewichtungsmultiplikator sind auf 0,1 bzw. 1,2 festgelegt. Diese Optionen sind unter Einstellungen | Datengewichtung verfügbar.
   7. Extrema-Datengewichtung: Um Datenpunkte um lokale Extrema (Spitzen und Täler) bevorzugt zu gewichten, wählen Sie die Anzahl der Datenpunkte aus, die jedes Extremum umgeben, auf das die bevorzugten Gewichtungen angewendet werden sollen, sowie den Gewichtungsmultiplikator für diese Punkte. Diese Punkte sind funktionsreicher, da sie direkt mit den angepassten Parametern verbunden sind. Suchen Sie nach Extrema-Datengewichtungseinstellungen unter Einstellungen | Datengewichtung , die als Standardeinstellung auf Ein eingestellt ist, und die Anzahl der Punkte und der Gewichtungsmultiplikator sind auf 5 bzw. 5 eingestellt. Um visuell zu identifizieren, welche Datenpunkte in der bevorzugten Gewichtung verwendet werden, wählen Sie Markante Datenpunkte ausfüllen aus.

5. Chromatizitäts- und Freie-Energie-Berechnungen

1. Stellen Sie sicher, dass die optimierte Anpassung der Daten und der zugehörigen Parameterwerte zufriedenstellend ist, bevor Sie mit zusätzlichen Berechnungen fortfahren. Klicken Sie zum Ausführen dieser Berechnungen auf die Schaltfläche Berechnen am unteren Rand des Bereichs Berechnungen .
   HINWEIS: Der erste zurückgegebene Wert, der als ΔG_ES (^cm-1) bezeichnet wird, ist die freie Energie des angeregten Zustands, der anhand der unten gezeigten Gleichung berechnet wird. Die Standardeinheit für diesen Wert ist inverse Zentimeter (^cm-1), aber es sind auch Einheiten für Elektronenvolt (eV) und Joule (J) verfügbar. Die Berechnung der freien Energie des angeregten Zustands ergibt sich aus der Gleichung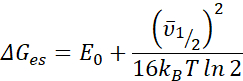
   
   1. Um die Einheit zu ändern, wählen Sie die gewünschte Option aus dem Dropdown-Listenfeld unter Einstellungen | Berechnungen aus. Dieser Wert wird basierend auf der Energiemenge (E₀), der vollen Breite bei halbem Maximum (Δv_1/2), der Boltzmann-Konstante (k_B) und der Umgebungstemperatur des Experiments (T) bestimmt. Der Wert für die experimentelle Temperatur wird mit 298 K angenommen, kann aber als 77 K oder eine andere Temperatur²⁰ angegeben werden.
      1. Um die Versuchstemperatur zu ändern, wählen Sie unter Einstellungen | Berechnungen | Versuchstemperatur die gewünschte Option.
         HINWEIS: Der zweite zurückgegebene Wert ist die CIE-Farbortkoordinate, berechnet aus dem aktuell ausgewählten Spektrum. Wenn dieser Wert in einem Farbortdiagramm dargestellt wird, zeigt er die vorhergesagte Farbe des aktiven Datenspektrums.
   2. Um das Farbwertdiagramm mit geplotteter Koordinate anzuzeigen, drücken Sie die Popup-Schaltfläche (dargestellt durch ein Quadrat mit einem Pfeil, der auf die obere rechte Ecke zeigt) neben dem Textfeld Farbwertkoordinate .
   3. Um die vorhergesagte Farbe der Probe zu überprüfen, verwenden Sie die dritte Berechnung, die als farbiges Rechteck dargestellt wird. Diese Schätzung basiert auf der gleichen Berechnung, die die Farbortkoordinate ergab. Standardmäßig wird CIE Standard Illuminant D65 verwendet, um diese Vorhersage zu treffen. Um das Leuchtmittel zu ändern, wählen Sie die gewünschte Option aus dem Dropdown-Menü Weißpunkt in Einstellungen | Berechnungen aus.
2. Um CIE-Farbwertkoordinaten und Farbwerte für mehrere geladene Spektren gleichzeitig zu berechnen, aktivieren Sie das entsprechende Kontrollkästchen unter Einstellungen | Berechnungen.
   HINWEIS: Diese Einstellung ist standardmäßig aktiviert. Sobald ein zweites Spektrum gezeichnet ist, ändert sich das Symbol auf der Popup-Schaltfläche neben der Beschriftung Chromatizitätskoordinate vom Quadrat mit einem Pfeil, der auf die obere rechte Ecke zeigt, zu drei Punkten (· · ·).
   1. Drücken Sie die Taste · · · , um ein Fenster mit der Bezeichnung Select Spectra (Spektren auswählen) anzuzeigen. Wählen Sie die gewünschten Spektren aus diesem Bereich aus und wählen Sie Werte als Tabelle und /oder Diagramm anzeigen , um das Farbwertdiagramm mit allen gezeichneten und beschrifteten Koordinaten anzuzeigen.

6. Datenexport

1. Stellen Sie erneut sicher, dass die Anpassung der geladenen Daten zufriedenstellend ist und dass alle gewünschten Berechnungen durchgeführt wurden. Um sowohl geladene als auch berechnete Daten zu exportieren, klicken Sie auf die Schaltfläche Daten exportieren. Es gibt sechs Datenexportoptionen: Abbildung, Parameterwerte, Spektrumdatenpunkte, Anpassungsdatenpunkte, Farbwerte und Farbwertdiagramm.
   1. Um das angezeigte Diagramm als für die Veröffentlichung oder Präsentation vorformatierte Abbildung zu exportieren, wählen Sie Abbildung. Diese Formatierung kann unter Einstellungen | Allgemein | Abbildungseinstellungen deaktiviert werden. Zu den unterstützten Dateitypen gehören . EPS (Vektorgrafikdatei), .JPG, .PNG und .PDF.
   2. Um alle Parameterwerte (mit oder ohne berechnete Werte) als Tabelle zu exportieren, wählen Sie Parameterwerte aus. Die Einbeziehung berechneter Werte kann unter Einstellungen | Berechnungen umgeschaltet werden und unterstützte Dateitypen sind . CSV, .TXT, . DAT, .XLS und . .XLSX.
   3. Um Daten des aktuell ausgewählten Spektrums als eine Reihe von x-y-Datenpunkten zu exportieren, wählen Sie Spektrumdatenpunkte. X-Werte verwenden entweder Wellenzahleinheiten (^cm-1) oder Wellenlängeneinheiten (nm), je nachdem, wie der Graph über die Einstellungen definiert ist. Die unterstützten Dateitypen sind die gleichen wie oben in 6.1.2.
   4. Um die Anpassung als eine Reihe von x-y-Datenpunkten zu exportieren, wiederum abhängig vom aktuellen Modus der Achsen, wählen Sie Datenpunkte anpassen. Die unterstützten Dateitypen sind die gleichen wie oben in 6.1.2.
   5. Um Farb- und CIE-Koordinaten sowie die vorhergesagte Farbe als RGB-Wert zu exportieren, wählen Sie Farbwerte, falls aktiviert. Die unterstützten Dateitypen sind die gleichen wie oben in 6.1.2.
   6. Um das Chromatizitätsdiagramm mit den darauf gezeichneten Farbortkoordinaten zu exportieren, die dem geladenen Spektrum zugeordnet sind, wählen Sie Chromatizitätsdiagramm. Unterstützte Dateitypen sind . EPS, .JPG, .PNG und .PDF.

Ergebnisse

Unter Verwendung der oben beschriebenen Anpassungsroutine wurde die Franck-Condon-Linienformanalyse an zwei Spektren durchgeführt, die mit der Anwendung vorverpackt sind: die Emissionsspektren Raumtemperatur (292 K) und niedrige Temperatur (77 K) für 9,10-Diphenylanthracen, gelöst in Toluol. Die Messungen wurden mit einem Spektrofluorometer mit flüssigen Lösungen in 1 cm Küvetten und einem Standard-Küvettenhalter für Raumtemperaturmessungen durchgeführt. Die Tieftemperaturmessungen wurden durch Eintauchen von NMR-Röhrchen in flüssigen Stickstoff in einem Dewar erhalten, um gefrorene Glasproben zu erzeugen. Alle Spektren wurden für die Detektorantwort korrigiert. Eine Singlemode-Anpassung war für das Raumtemperaturspektrum ausreichend, während der Doppelmodus zur Modellierung des Niedertemperaturspektrums verwendet wurde. Die Farbanalyse wurde für beide Spektren durchgeführt und ergab ähnliche Schätzungen.

Um dem Raumtemperaturspektrum gerecht zu werden, wurde die manuelle Anpassung nach der Optimierung der kleinsten Quadrate mit Standardanpassungen verwendet. Die endgültigen Parameterwerte waren wie folgt: E₀ = 24380 cm-1, Δv 1_/2 = 1200 cm-1, S = 1,25, ħω = 1280 ^cm-1. Der errechnete Bestimmtheitskoeffizient betrug 0,99947, wie in Abbildung 1 dargestellt. Die Berechnung der freien Energie des angeregten Zustands mit diesen Parameterwerten ergab einen Wert von 25.000 ^cm-1.

Simplex-Optimierung wurde verwendet, um das niedrige Temperaturspektrum anzupassen. Eine manuelle Anpassung war nach der Optimierung nicht notwendig. Die endgültigen Parameterwerte waren wie folgt: E 0 = 24764 cm-1, Δv 1/2 = 746 cm-1, S 1= 1,13, ħω 1 = ₁₃₈₂ cm-1, S₂ = _0,31, ħω₂= 651 ^cm-1. Der errechnete Bestimmtheitskoeffizient betrug 0,9991, wie in Abbildung 2 dargestellt. Die Berechnung der freien Energie des angeregten Zustands mit diesen Parameterwerten ergab einen Wert von 25.700 ^cm-1.

Die Farbanalyse des Tieftemperaturspektrums ergab folgende Ergebnisse: Farbortkoordinate = [0,15819, 0,03349], CIE-Koordinate = [0,19571, 0,041432, 1] und vorhergesagter RGB-Wert = [67, 0, 233]. Die für das Raumtemperaturspektrum erhaltenen Werte waren denen des Tieftemperaturspektrums mit nicht wahrnehmbaren Farbunterschieden sehr ähnlich.

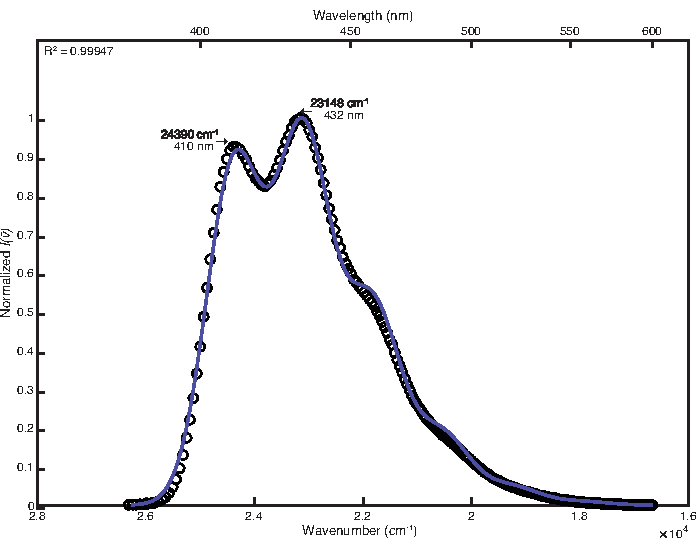
Abbildung 1: Singlemode-Fit von 9,10-Diphenylanthracen (292 K): Diese Abbildung zeigt das Raumtemperatur-Emissionsspektrum von 9,10-Diphenylanthracen und seine FCLSA-Fit-Funktion, erreicht durch Least-Squares-Optimierung gefolgt von Handeinstellung der Parameterwerte. Dies ist ein Beispiel für ein lose strukturiertes Spektrum. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.

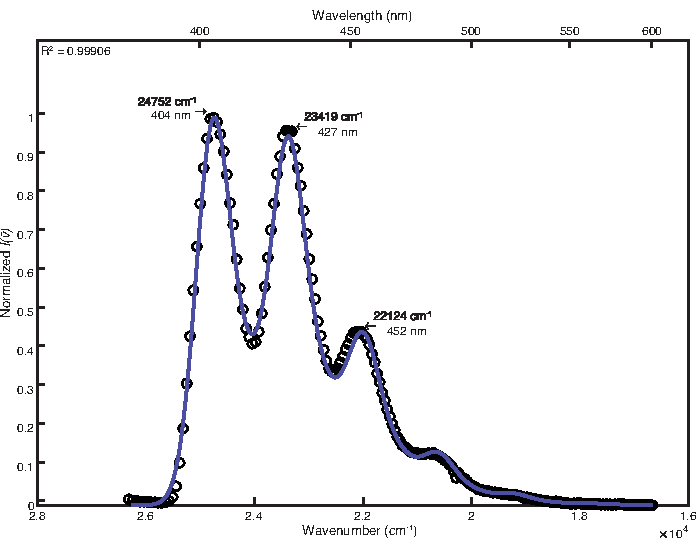
Abbildung 2: Doppelmodenanpassung von 9,10-Diphenylanthracen (77 K): Diese Abbildung zeigt das Niedertemperatur-Emissionsspektrum von 9,10-Diphenylanthracen und seine FCLSA-Fit-Funktion, die durch eine Simplex-Optimierung erreicht wird. Dies ist ein Beispiel für ein stark strukturiertes Spektrum. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.

Diskussion

Diese Anwendung bietet eine einfache und schnelle Analyse von Emissionsspektren durch zwei Hauptmethoden, die üblicherweise in der photophysikalischen Gemeinschaft verwendet werden. Die erste ist die Franck-Condon-Linienformanalyse (FCLSA), die einen Einblick in die Energetik und vibronische Kopplung gibt, die mit dem Zerfall angeregter Zustandsmoleküle in ihren Grundzustand verbunden sind. Dies wird durch die Optimierung von Parameterwerten erreicht, um die Anpassungsgüte eines Spektrums unter Verwendung einer von zwei möglichen FCLSA-Modellierungsgleichungen zu maximieren. Die zweite Analysemethode gibt Aufschluss über die beobachtete Farbe des vom Molekül emittierten Lichts. Durch die Kombination von Tristimulus-Farbkurven mit bereitgestellten Intensitätsdaten kann die CIE-Koordinate berechnet werden. Diese Bestimmung ermöglicht die hochgenaue Farbvorhersage von Absorptions- und Emissionsspektren.

Experimentelle Photolumineszenzspektren werden üblicherweise mit einer Photomultiplierröhre (PMT) oder einem ladungsgekoppelten Gerät (CCD) als Detektor gemessen und als Emissionsintensität versus Wellenlänge (nm) dargestellt. Viele photophysikalische Charakterisierungen, einschließlich FCLSA und Berechnung der freien Energie des angeregten Zustands, werden im Wellenzahlraum durchgeführt, wie die Verwendung von 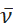(^cm-1) in den entsprechenden Gleichungen oben zeigt. Zusätzlich zur Umrechnung der x-Achse muss die als I(λ) bezeichnete Emissionsintensität gegenüber der Wellenlänge in 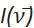umgerechnet werden. Diese Anwendung identifiziert automatisch die ursprünglichen x-Achsen-Einheiten importierter Spektraldaten als Wellenlänge (nm) oder Wellenzahl (^cm-1). Standardmäßig konvertiert die Anwendung dann die Spektraldaten, normalisiert das Spektrum bei maximaler Intensitätsspitze in Einheit und stellt das Spektrum als "Normalisierte 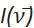vs. Wellenzahl (^cm-1)" dar, um anzuzeigen, dass die korrekte Intensitätskonvertierung angewendet wurde. Obwohl empfohlen wird, alle Anpassungen mit Wellenzahleinheiten durchzuführen, kann die Anwendung das Spektrum auch als "Normalized I(λ) vs. wavelength (nm)" darstellen, indem sie die Anweisungen in Abschnitt 2 oben befolgt.

Für die Verwendung in der Anwendung stehen zwei Optimierungsalgorithmen zur Verfügung. Die Standardoption ist gedämpfte kleinste Quadrate, die den Levenberg-Marquardt-Algorithmus²¹ verwendet. Durch die Kombination einer Version des Gradientenabstiegs und des Gauß-Newton-Algorithmus findet dieser Algorithmus lokale, nicht unbedingt globale Minima. Obwohl dies eine erhebliche Einschränkung ist, bietet der Algorithmus Vorteile in seiner Anpassbarkeit - diese Methode kann die bevorzugte Gewichtung von Datenpunkten berücksichtigen, eine robuste Anpassung durchführen und erweiterte Statistiken zur Güte der Anpassung anzeigen²². Die alternative Optimierungsmethode ist derivativfrei und basiert auf dem Nelder-Mead-Simplex-Algorithmus²³. Dieser Algorithmus verwendet eine heuristische Methode, um ein globales Minimum der angegebenen Kostenfunktion zurückzugeben (in diesem Fall eine Summe der quadrierten Differenzen zwischen vorhergesagten und beobachteten Intensitäten). Die Simplex-Methode wurde bereits für FCLSA verwendet, obwohl der Code, der sie implementiert, nie veröffentlicht wurde²⁴.

Sowohl die Least-Squares- als auch die Simplex-Optimierungsmethoden eignen sich am besten für strukturierte Spektren, die schmale, gut definierte und symmetrische Peaks aufweisen. Da Spektren weniger strukturiert werden, was bedeutet, dass sie an Symmetrie verlieren und sich die Peaks erweitern, führen diese Methoden zu weniger robusten Anpassungen, bei denen die Parameter stark korreliert werden können. Typischerweise sind Spektren, die bei niedrigen Temperaturen oder in starren Medien aufgezeichnet wurden, strukturierter als diejenigen, die bei Raumtemperatur oder in flüssiger Lösung 12,25,26 erhalten wurden. Die robusten Passformoptionen, die in der Methode der kleinsten Quadrate enthalten sind, können dazu beitragen, dieses Problem zu lindern. Dieses Problem kann erheblich verringert werden, wenn einer oder mehrere der Parameter während der Optimierung auf einen konstanten Wert festgelegt werden. Zum Beispiel können IR-Spektroskopie-Experimente verwendet werden, um relevante Quantenabstandswerte (ħω) zu bestimmen. Alternativ können relevante Literaturwerte verwendet werden, um benutzerdefinierte Grenzen für die Parameter festzulegen.

In einigen Fällen stellen die FCLSA-Anpassung und die aus den Optimierungsroutinen erhaltenen Parameter die Daten nicht angemessen dar, selbst wenn robuste Anpassungsoptionen oder feste Parameter verwendet werden. Dies ist ein Fehler der Anpassungsalgorithmen und kann mit den mehreren FCLSA-Anpassungsparametern (potenzielle Überparametrierung) oder der spektralen Form der Daten (merkmallose Spektren) zusammenhängen. In diesen Fällen kann eine weitere Verbesserung der Passungen durch eine "manuelle Anpassung" der Daten unter Manipulation der FCLSA-Parameter erreicht werden. Die Angemessenheit solcher Anpassungen kann visuell beurteilt und quantifiziert werden, indem Statistiken zur Güte der Anpassung verglichen werden, die automatisch in das Diagramm aufgenommen werden.

Eine allgemeine Routine für eine genaue Anpassung von Hand besteht aus den folgenden fünf Schritten: Ermitteln Sie zunächst manuell oder automatisch eine erste Schätzung für E₀ mit einer der drei bereitgestellten Methoden. Standardmäßig wird der Wert des Parameters der Wellenzahl zugewiesen, die der höchsten beim Datenimport erkannten Intensitätsspitze zugeordnet ist. Alternativ kann der Benutzer E₀ als die Wellenzahl definieren, bei der das Emissionsspektrum sein entsprechendes Anregungsspektrum schneidet. Die letzte Methode zur Bestimmung von E₀ verwendet die sogenannte X%-Regel, wobei X = 1 oder 10 ist. Bei dieser Methode wird E₀ einer Wellenzahl X% der vollen Breite bei halbmaximaler (FWHM) Intensität des prominentesten Datenpeaks unter Annahme einer Gaußschen Bandform zugewiesen. Der zweite Schritt im manuellen Anpassungsprotokoll besteht darin, ħω basierend auf Quantenabständen zu berechnen, die in der Struktur des Emissionsspektrums beobachtet wurden. Wenn möglich, beziehen Sie sich auf das IR-Spektrum des Moleküls und versuchen Sie, den Photolumineszenz-basierten Wert mit einer starken Bande im IR-Spektrum zu korrelieren. Drittens bestimmen Sie S basierend auf den relativen Intensitäten der spektralen Peaks. Viertens, bestimmen Sie ein grobes Δv_1/2 basierend auf der Bandbreite. Fünftens: S und Δv_1/2 bei Bedarf iterativ nachjustieren.

Die Schwierigkeit, FCLSA mit breiten, relativ merkmallosen Spektren durchzuführen, wurde durch das Anpassungsverfahren für 9,10-Diphenylanthracen in flüssiger Lösung bei 292 K im Vergleich zu dem Verfahren für das strukturiertere Spektrum in gefrorenem Glas bei 77 K demonstriert. Bei der Anpassung des Raumtemperaturspektrums ergab die Optimierung einen anfänglichen Bestimmtheitskoeffizienten von 0,9971, der durch manuelle Abstimmung der Parameter und visuelle Inspektion der Ergebnisse auf 0,9994 verbessert wurde. Im Gegensatz dazu war eine manuelle Anpassung der Niedertemperaturvariante aufgrund der Feinstruktur des Spektrums nicht erforderlich, was nach der Simplexoptimierung zu einem Bestimmtheitskoeffizienten von 0,9991 führte.

In vielen Fällen liefern beide Optimierungsroutinen (kleinste Quadrate und Simplex) sehr ähnliche Ergebnisse. Dies deutet darauf hin, dass sie ein globales Minimum für die FCLSA-Parameter gefunden haben. Im Allgemeinen ist die Methode der kleinsten Quadrate tendenziell besser für Daten geeignet, die verrauscht sind, nicht gut strukturiert sind oder viele Datenpunkte nahe Null am Ende des Spektrums enthalten. Umgekehrt gibt die Simplex-Methode tendenziell bessere Anpassungen zurück als die Methode der kleinsten Quadrate für Daten, die gut strukturiert sind und nur wenige Ausreißerpunkte aufweisen. In diesen Fällen erfordert die Simplex-Methode typischerweise wenig manuelle Voroptimierung der Parameterwerte und keine Anpassung nach der Optimierung. Für die Fälle, in denen das Rauschen der Daten oder der allgemeine Mangel an Struktur eine qualitativ hochwertige Anpassung mit einer der bereitgestellten Optimierungsmethoden verhindert, wird empfohlen, die manuelle Anpassungsmethode (siehe oben) ohne nachträgliche Optimierung anzuwenden.

Diese Anwendung bietet mehrere Vorteile gegenüber früheren Implementierungen der Franck-Condon-Linienformanalyse. Der erste und wichtigste Vorteil ist, dass es kostenlos, öffentlich zugänglich und vollständig transparent ist. Dies wird erreicht, indem der Code auf GitHub veröffentlicht wird, wodurch jeder mit einem Computer und einer Internetverbindung (https://github.com/USArmyResearchLab/ARL_Spectral_Fitting) Zugriff erhält. Jeder kann nicht nur auf diese Anwendung zugreifen, sondern auch den zugrunde liegenden Code anzeigen. Dies bietet die Möglichkeit für Feedback und Entwicklung aus der Community. Ein weiterer Vorteil liegt in der Benutzerfreundlichkeit dieser Anwendung. Es sind keine Hintergrundkenntnisse in Informatik oder Befehlszeileninteraktion erforderlich. Vielmehr verwendet diese Software eine einfache grafische Benutzeroberfläche (GUI), die es Forschern aller Hintergründe ermöglicht, die oben beschriebenen Spektralanalysen durchzuführen. Darüber hinaus bietet diese Anwendung dem Benutzer mehrere Möglichkeiten zur Steuerung der Optimierungsmethoden und kann verwendet werden, um die freie Energie des angeregten Zustands zu bestimmen. Schließlich berechnet und meldet die Software mehrere nützliche Farbwerte, darunter Farbortkoordinaten, CIE-Koordinaten, RGB und hexadezimale Farbcodes. Alle diese Analysen können in Sekunden durchgeführt werden, wobei der Benutzer nur einen Knopfdruck erfordert.

Materialien

Name	Company	Catalog Number	Comments
ARL Spectral Fitting	Army Research Laboratory	v1.0	https://github.com/USArmyResearchLab/ARL_Spectral_Fitting/releases/tag/v1.0