ARL Spectral Fitting come applicazione per aumentare i dati spettrali tramite l'analisi lineshape di Franck-Condon e l'analisi del colore

Riepilogo

Questo protocollo introduce Franck-Condon Lineshape Analyses (FCLSA) degli spettri di emissione e funge da tutorial per l'uso del software ARL Spectral Fitting. Il software open source fornisce un modo semplice e intuitivo per eseguire analisi avanzate degli spettri di emissione, inclusi calcoli di energia allo stato eccitato, determinazione delle coordinate di colore CIE e FCLSA.

Abstract

L'applicazione ARL Spectral Fitting fornisce un metodo gratuito, accessibile al pubblico e completamente trasparente per eseguire l'analisi della forma della linea di Franck-Condon (FCLSA) sui dati spettrali, oltre alla determinazione delle coordinate di colore CIE e all'elaborazione spettrale di base. Mentre alcune delle caratteristiche possono essere trovate in software commerciali o in programmi realizzati da gruppi di ricerca accademici, riteniamo che ARL Spectral Fitting sia l'unica applicazione che possiede tutti e tre gli attributi di cui sopra.

Questo programma è inteso come un'applicazione autonoma basata su GUI per l'uso da parte di un ricercatore di laboratorio medio senza richiedere alcuna conoscenza di codifica o software proprietario. Oltre all'eseguibile autonomo ospitato su ARL GitHub, i file MATLAB associati sono disponibili per l'uso e l'ulteriore sviluppo.

FCLSA aumenta le informazioni trovate negli spettri di luminescenza, fornendo informazioni significative sulla relazione tra il terreno e gli stati eccitati di una specie fotoluminescente. Questa intuizione si ottiene modellando gli spettri con due versioni (modalità) di un'equazione caratterizzate da quattro o sei parametri, a seconda della modalità utilizzata. Una volta ottimizzato, il valore di ciascuno di questi parametri può essere utilizzato per ottenere informazioni sulla molecola, nonché per eseguire ulteriori analisi (ad esempio, il contenuto di energia libera della molecola allo stato eccitato). Questa applicazione fornisce strumenti per un facile adattamento manuale dei dati importati, nonché due metodi per ottimizzare questo adattamento ai minimi quadrati smorzato, alimentato dall'algoritmo di Levenberg-Marquardt e il fitting senza derivate che utilizza l'algoritmo simplesso di Nelder-Mead. Inoltre, le stime del colore del campione possono essere eseguite e riportate in coordinate CIE e RGB.

Introduzione

Le misure di fotoluminescenza, che comprendono sia spettri di fluorescenza che di fosforescenza, sono ampiamente utilizzate in vari campi accademici e applicazioni industriali¹. I fotocatalizzatori sono sempre più utilizzati nella sintesi organica per la produzione di molecole bersaglio complesse e preziose ^2,3,4. Al fine di determinare l'energetica dei fotocatalizzatori, l'energia dello stato eccitato viene regolarmente stimata utilizzando spettri di emissione. Lo sviluppo di nuovi materiali di illuminazione, come i luminofori OLED (organic light emitting diode), richiede che l'output cromatico osservato sia caratterizzato e riportato ^5,6. Le coordinate cromatiche della Commission international de l'éclairage (CIE) sono abitualmente utilizzate a tale scopo⁷.

Lo scopo dell'applicazione ARL Spectral Fitting è quello di fornire un metodo rapido e semplice per aumentare i dati spettrali attraverso un'analisi significativa che sia ampiamente accessibile sia in termini di facilità d'uso che di disponibilità (https://github.com/USArmyResearchLab/ARL_Spectral_Fitting). Questo software esegue automaticamente diverse funzioni di elaborazione spettrale di routine per l'utente, tra cui la normalizzazione dei dati e la conversione tra lunghezze d'onda, λ e numero d'onda, , 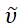unità con scala di intensità appropriata come mostrato nell'equazione sotto¹. Il software è in grado di gestire una varietà di formati di file di input e output. Diverse analisi avanzate sono facilmente eseguibili utilizzando il software come il calcolo delle coordinate CIE e cromatiche, la previsione del colore, la determinazione dell'energia libera dello stato eccitato (ΔG_ES) in varie unità e FCLSA per la determinazione dei parametri FCLSA⁸.

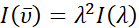
È stata perseguita un'applicazione basata su interfaccia utente grafica (GUI) perché consente a qualsiasi ricercatore di eseguire questa analisi e non richiede alcuna conoscenza di base dell'informatica. Questa applicazione è stata scritta in MATLAB, utilizzando il suo strumento App Designer. Al di fuori di ARL Spectral Fitting, trovare un'implementazione accessibile al pubblico di un'applicazione progettata per eseguire l'analisi lineshape di Franck-Condon è praticamente impossibile. Questo perché i gruppi di ricerca non rilasciano pubblicamente le loro implementazioni, preferendo invece mantenerle proprietarie.

L'analisi lineshape di Franck-Condon (FCLSA) è spesso utilizzata nella caratterizzazione fotofisica di nuovi composti a causa delle ricche informazioni che trasmette sulla molecola 9,10,11,12,13,14. Ciascuno dei quattro parametri (sei se in modalità doppia) fornisce informazioni sullo stato eccitato della molecola. La quantità di energia, o gap energetico 0-0, (E₀) è la differenza nei livelli di energia zero del terreno e degli stati eccitati della molecola. L'intera larghezza a metà massimo (Δv_1/2)  informa sulle larghezze delle singole linee vibroniche. La costante di accoppiamento elettrone-vibrazionale, o fattore di Huang-Rhys, (S) è un calcolo adimensionale basato sullo spostamento di equilibrio tra gli stati di terra ed eccitato della molecola¹⁵. Infine, il parametro di spaziatura quantistica (ħω) è la distanza tra i modi vibrazionali che governano il decadimento non radiativo di una molecola.

Le equazioni per FCLSA in modalità singola e doppia sono le seguenti:

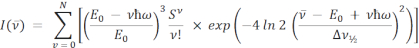
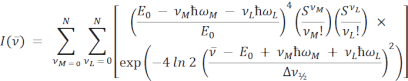
dove i parametri sono quelli definiti in precedenza. Nell'equazione a doppio modo, S e ħω sono separati in termini di energia media (_M) e bassa (_L). 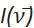è l'intensità al numero d'onda v^10,16,17,18. In entrambe le equazioni, la sommatoria viene eseguita su N livelli quantici con un valore predefinito di N = 5, come è comunemente usato nella letteratura¹¹, ma qualsiasi intero può essere specificato nel software ARL Spectral Fitting in Impostazioni | In forma.

Protocollo

1. Importazione dei dati

1. Per importare i dati, premere il pulsante Importa dati . Selezionare il tipo di spettro da importare: eccitazione o emissione.
   1. Una volta scelto un tipo di spettro, assicurati che venga visualizzato l'esploratore di file MATLAB. Da questa finestra, selezionare il file desiderato e premere Apri. I tipi di file supportati includono .TXT, . CSV, .XLS e . .XLSX.
      NOTA: alcune elaborazioni dei dati vengono eseguite automaticamente prima di tracciare i dati importati. Ciò include: rilevamento di unità dell'asse x (numero d'onda o lunghezza d'onda) e conversione in numero d'onda, se appropriato; normalizzazione dell'intensità del picco più alto a 1; calcolo della quantità di energia, se del caso; e stima della spaziatura quantistica. Questi valori sono calcolati in base ai picchi di dati rilevati con quantità di energia assegnata al valore del numero d'onda del picco di energia più alto e spaziatura quantistica basata sulla distanza media tra i picchi vicinali, che richiede il rilevamento di almeno due picchi.
2. Per caricare uno qualsiasi degli spettri campione preconfezionati, premere il pulsante corrispondente allo spettro desiderato, che si trova in Info | Spettri di esempio. Nove spettri campione vengono preconfezionati con l'applicazione.
3. Per caricare e tracciare più di uno spettro alla volta, attivare la casella di controllo Consenti spettri dati multipli sugli assi in Impostazioni | | generale Impostazioni figura.
4. Per selezionare uno spettro caricato diverso da quello attualmente attivo, premere il pulsante Seleziona spettro da adattare , quindi scegliere lo spettro desiderato dall'elenco visualizzato nel pannello Seleziona spettro appena visibile.

2. Trattamento dei dati

NOTA: L'utente potrebbe voler eseguire l'elaborazione dei dati prima del processo di adattamento. I processi disponibili includono:

1. Selezione di un picco che funga da base per la normalizzazione: per selezionare un picco che funga da base per la normalizzazione dell'intensità, premere il pulsante Seleziona picco per la normalizzazione che si trova in Impostazioni | Generale. Seguire le istruzioni visualizzate sullo schermo. Il picco predefinito per la normalizzazione dell'intensità è il picco di intensità più alto rilevato durante l'importazione.
2. Conversione tra unità dell'asse x: per convertire le unità dell'asse x tra numero d'onda (^cm-1) e lunghezza d'onda (nm), attivare o disattivare il dispositivo di scorrimento disponibile in Impostazioni | Asse X alla modalità desiderata ( Numero d'onda o Lunghezza d'onda). L'intensità e le unità dell'asse x saranno regolate per tutti gli spettri caricati, utilizzando l'equazione sopra indicata.
3. Vincolo dell'intervallo dell'asse x: per vincolare manualmente l'intervallo dell'asse x, selezionare Regola manualmente l'asse X e adatta limiti in Impostazioni | Asse X. Quindi, utilizzare i controlli rivelati per specificare l'intervallo dell'asse x. Per impostazione predefinita, l'applicazione espanderà e contrarrà automaticamente l'intervallo dell'asse x per adattarsi a tutti i punti dati caricati.
4. Metodi di calcolo alternativi E₀ : per selezionare un metodo di calcolo alternativo per la quantità di energia, selezionare il metodo desiderato che si trova in Impostazioni | In forma. Il metodo predefinito è Full FCLSA fit. Per passare a un altro metodo, selezionare il pulsante radiale corrispondente e seguire le istruzioni visualizzate sullo schermo¹⁹.

3. Montaggio manuale

NOTA: In base alla quantità di struttura visibile nello spettro, può essere molto vantaggioso inizializzare i parametri di adattamento con stime appropriate prima dell'ottimizzazione. Questa inizializzazione può ridurre il tempo necessario per l'ottimizzazione e garantisce che i valori restituiti dall'ottimizzazione siano realistici per lo spettro.

1. Tracciate la funzione di adattamento con i valori dei parametri correnti premendo il pulsante Funzione di adattamento (Plot Fit Function ).
2. Utilizzando una combinazione dei pulsanti di regolazione grossolani e fini, dei cursori e dei campi di modifica, regolare i valori dei parametri per aumentare la bontà di adattamento per i dati caricati. Per impostazione predefinita, il coefficiente di determinazione (R²) viene visualizzato nell'angolo superiore sinistro del grafico. Utilizzare questo come misura quantitativa della bontà dell'adattamento per guidare la scelta dei valori dei parametri.
   NOTA: poiché la quantità di energia (E₀) e la spaziatura quantistica (ħω) vengono calcolate dall'applicazione al momento dell'importazione dei dati, si consiglia di mantenere questi valori costanti o minimamente variati quando vengono adattati manualmente.
3. Per impostazione predefinita, questa applicazione utilizza la formula di analisi lineshape di Franck-Condon in modalità singola in quanto è più rilevante per gli spettri di temperatura ambiente. Se lo si desidera, ad esempio quando si adattano spettri a 77 K, passare dalla modalità singola a quella doppia in Impostazioni | In forma.
   NOTA: la sovraparametrizzazione diventa un problema maggiore quando si adatta in modalità doppia rispetto alla modalità singola a causa dell'aumento del numero di valori dei parametri fluttuanti. Spettri di emissione ampi e privi di struttura pongono il problema più grande agli algoritmi di adattamento e possono comportare una correlazione incrociata tra i parametri FCLSA, in particolare tra Δv_1/2 e S. Quando si adattano gli spettri, è imperativo che i parametri FCLSA ottenuti siano verificati per essere fisicamente realistici utilizzando la precedenza della letteratura come guida.

4. Ottimizzazione

1. Dopo aver trovato parametri iniziali soddisfacenti, è possibile eseguire un'ulteriore ottimizzazione. Per fare ciò, premere il pulsante blu Ottimizza adattamento . L'ottimizzazione eseguirà e ricomprimerà la funzione di adattamento con i valori dei parametri ottimizzati di recente.
2. Sono disponibili due opzioni di ottimizzazione: i metodi dei minimi quadrati e dei simplessi. Per passare da un metodo all'altro, passare al metodo desiderato in Impostazioni | ottimizzazione.
3. Se lo si desidera, personalizzare il metodo di ottimizzazione utilizzando le impostazioni disponibili in Impostazioni | Ottimizzazione.
   NOTA: per consentire all'utente di controllare le routine di ottimizzazione, sono possibili le seguenti opzioni di personalizzazione per entrambi i metodi di ottimizzazione:
   1. Correggere i valori di un parametro: per correggere il valore di un parametro durante l'ottimizzazione, premere la casella di controllo nel campo di modifica corrispondente al parametro desiderato.
   2. Delimitazione personalizzata di un parametro durante l'ottimizzazione: per visualizzare le opzioni di delimitazione personalizzate, attivare la casella di controllo Consenti delimitazione parametri personalizzati durante l'ottimizzazione in Impostazioni | ottimizzazione. Per specificare limiti personalizzati per il valore di un parametro durante l'ottimizzazione, utilizzare i controlli visualizzati premendo il pulsante Limiti personalizzati sotto il campo di modifica corrispondente al parametro desiderato.
   3. Trigger finali personalizzati per l'ottimizzazione: per regolare il numero massimo di iterazioni, la tolleranza di terminazione sul valore del modello o la tolleranza di terminazione sui valori del coefficiente, attivare la casella di controllo corrispondente in Impostazioni | ottimizzazione e immettere il valore desiderato nel campo di modifica corrispondente.
      NOTA: le seguenti personalizzazioni sono disponibili solo per l'ottimizzazione dei minimi quadrati :
   4. Statistiche sulla bontà dell'adattamento: per visualizzare le statistiche sulla bontà dell'adattamento (coefficiente di determinazione regolato del grado di libertà, somma dei quadrati dovuti all'errore, gradi di libertà nell'errore ed errore quadratico medio radice) al termine dell'ottimizzazione, attivare la casella di controllo disponibile in Impostazioni | ottimizzazione.
   5. Opzioni di adattamento robuste: per attivare opzioni di adattamento robuste, selezionare il menu desiderato dall'elenco a discesa in Impostazioni | ottimizzazione. Per impostazione predefinita, questa opzione è disattivata. Se lo si desidera, attivare il raccordo Least Absolute Residual o Bisquare Weights, che conferisce un peso inferiore ai punti dati anomali.
   6. Ponderazione dei dati di soglia: per pesare preferenzialmente i punti dati al di sopra di un'intensità di soglia, scegliere un'intensità che funga da soglia e un moltiplicatore di peso da applicare a tutti i punti al di sopra di tale soglia. Per impostazione predefinita, questa opzione è impostata su on e il moltiplicatore di soglia e peso è impostato rispettivamente su 0,1 e 1,2. Queste opzioni sono disponibili in Impostazioni | Ponderazione dati.
   7. Ponderazione dei dati Extrema: per ponderare preferenzialmente i punti dati relativi agli estremi locali (picchi e valli), selezionare il numero di punti dati che circondano ciascun estremo a cui applicare i pesi preferenziali, nonché quale dovrebbe essere il moltiplicatore di peso per tali punti. Questi punti sono più ricchi di funzionalità in quanto sono direttamente associati ai parametri adattati. Cerca le impostazioni di ponderazione dei dati extrema in Impostazioni | Ponderazione dati che è impostata su on come impostazione predefinita e il numero di punti e il moltiplicatore di peso sono impostati rispettivamente su 5 e 5. Per identificare visivamente quali punti dati vengono utilizzati nella ponderazione preferenziale, selezionare Riempi punti dati salienti.

5. Calcoli di cromaticità ed energia libera

1. Assicurarsi che l'adattamento ottimizzato dei dati e i valori dei parametri associati siano soddisfacenti prima di procedere a ulteriori calcoli. Per eseguire questi calcoli, premere il pulsante Calcola , situato nella parte inferiore del riquadro Calcoli .
   NOTA: Il primo valore restituito, etichettato ΔG_ES (^cm-1), è l'energia libera dello stato eccitato calcolata utilizzando l'equazione mostrata di seguito. L'unità predefinita per questo valore è centimetri inversi (^cm-1), ma sono disponibili anche unità di elettronvolt (eV) e joule (J). Il calcolo per l'energia libera dello stato eccitato è dato dall'equazione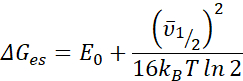
   
   1. Per cambiare l'unità, selezionare l'opzione desiderata dalla casella di riepilogo a discesa che si trova in Impostazioni | calcoli. Questo valore è determinato in base alla quantità di energia (E₀), alla larghezza completa a metà max (Δv_1/2), alla costante di Boltzmann (k_B) e alla temperatura ambientale dell'esperimento (T). Si presume che il valore per la temperatura sperimentale sia 298 K, ma può essere specificato come 77 K o qualsiasi altra temperatura²⁰.
      1. Per modificare la temperatura sperimentale, scegliere l'opzione desiderata in Impostazioni | calcoli | Temperatura sperimentale.
         NOTA: il secondo valore restituito è la coordinata di cromaticità CIE, calcolata dallo spettro attualmente selezionato. Quando viene tracciato su un diagramma di cromaticità, questo valore mostra il colore previsto dello spettro di dati attivi.
   2. Per visualizzare il diagramma di cromaticità con le coordinate tracciate, premere il pulsante pop-out (rappresentato da un quadrato con una freccia rivolta verso l'angolo superiore destro) accanto alla casella di testo Coordinate cromatiche .
   3. Per verificare il colore previsto del campione, utilizzare il terzo calcolo, visualizzato come rettangolo colorato. Questa stima si basa sullo stesso calcolo che ha prodotto la coordinata di cromaticità. Per impostazione predefinita, CIE Standard Illuminant D65 viene utilizzato per effettuare questa previsione. Per cambiare l'illuminante, selezionare l'opzione desiderata dal menu a discesa denominato Punto bianco in Impostazioni | calcoli.
2. Per calcolare le coordinate di cromaticità CIE e i valori di colore per più spettri caricati contemporaneamente, attivare la casella di controllo corrispondente che si trova in Impostazioni | calcoli.
   NOTA: questa impostazione è attiva per impostazione predefinita. Una volta tracciato un secondo spettro, l'icona sul pulsante pop-out accanto all'etichetta Coordinate di cromaticità cambierà dal quadrato con una freccia che punta all'angolo in alto a destra a tre punti (· · ·).
   1. Premete il pulsante · · · per visualizzare un pannello con l'etichetta Seleziona spettrale. Selezionare gli spettri desiderati da questo pannello e scegliere Esporta valori come tabella e/o diagramma di visualizzazione per visualizzare il diagramma di cromaticità con tutte le coordinate tracciate ed etichettate.

6. Esportazione dei dati

1. Ancora una volta, assicurarsi che l'adattamento dei dati caricati sia soddisfacente e che tutti i calcoli desiderati siano stati eseguiti. Per esportare sia i dati caricati che quelli calcolati, premere il pulsante Esporta dati . Sono disponibili sei opzioni di esportazione dei dati: Figura, Valori parametri, Punti dati spettro, Punti dati adatta, Valori colore e Diagramma cromaticità.
   1. Per esportare il grafico visualizzato come figura preformattata per la pubblicazione o la presentazione, selezionare Figura. Questa formattazione può essere disabilitata in Impostazioni | Impostazioni generali | Figure. I tipi di file supportati includono . EPS (file di grafica vettoriale), .JPG, .PNG e .PDF.
   2. Per esportare tutti i valori dei parametri, con o senza valori calcolati, come tabella, selezionare Valori parametro. L'inclusione dei valori calcolati è attivabile in Impostazioni | calcoli e i tipi di file supportati sono . CSV, .TXT, . DAT, .XLS e . .XLSX.
   3. Per esportare i dati dello spettro attualmente selezionato come serie di punti dati x-y, selezionare Punti dati spettro. I valori X utilizzeranno unità di numero d'onda (^cm-1) o lunghezza d'onda (nm), a seconda di come viene definito il grafico tramite le impostazioni. I tipi di file supportati sono gli stessi di cui sopra nella versione 6.1.2.
   4. Per esportare l'adattamento come una serie di punti dati x-y, sempre in base alla modalità corrente degli assi, selezionare Adatta punti dati. I tipi di file supportati sono gli stessi di cui sopra nella versione 6.1.2.
   5. Per esportare la cromaticità e le coordinate CIE, nonché il colore previsto come valore RGB, se abilitato, selezionare Valori colore. I tipi di file supportati sono gli stessi di cui sopra nella versione 6.1.2.
   6. Per esportare il diagramma di cromaticità con le coordinate di cromaticità tracciate su di esso associate allo spettro caricato, selezionare Diagramma di cromaticità. I tipi di file supportati sono . EPS, .JPG, .PNG e .PDF.

Risultati

Utilizzando la routine di adattamento sopra descritta, l'analisi della linea di Franck-Condon è stata eseguita su due spettri preconfezionati con l'applicazione: gli spettri di emissione a temperatura ambiente (292 K) e a bassa temperatura (77 K) per 9,10-difenilantracene disciolto in toluene. Le misurazioni sono state ottenute utilizzando uno spettrofluorometro con soluzioni fluide in cuvette da 1 cm e un supporto per cuvetta standard per misure a temperatura ambiente. Le misurazioni a bassa temperatura sono state ottenute immergendo tubi NMR in azoto liquido in un dewar per generare campioni di vetro congelato. Tutti gli spettri sono stati corretti per la risposta del rivelatore. Un adattamento a modalità singola era sufficiente per lo spettro della temperatura ambiente, mentre la modalità doppia è stata utilizzata per modellare lo spettro delle basse temperature. L'analisi del colore è stata eseguita su entrambi gli spettri e ha prodotto stime simili.

Per adattarsi allo spettro della temperatura ambiente, è stata utilizzata la regolazione manuale dopo l'ottimizzazione dei minimi quadrati con personalizzazioni predefinite. I valori finali dei parametri ottenuti sono stati i seguenti: E₀ = 24380 cm-1, Δv 1_/2 = 1200 cm-1, S = 1,25, ħω = 1280 ^cm-1. Il coefficiente di determinazione risultante calcolato è stato 0,99947, come mostrato nella figura 1. Il calcolo dell'energia libera dello stato eccitato utilizzando questi valori di parametro ha prodotto un valore di 25.000 ^cm-1.

L'ottimizzazione del simplesso è stata utilizzata per adattarsi allo spettro delle basse temperature. La regolazione manuale non è stata necessaria dopo l'ottimizzazione. I valori finali dei parametri ottenuti sono stati i seguenti: E 0 = 24764 cm-1, Δv 1/2 = 746 cm-1, S 1= 1,13, ħω 1 = ₁₃₈₂ cm-1, S₂ = _0,31, ħω₂= 651 ^cm-1. Il coefficiente di determinazione risultante calcolato è stato 0,9991, come mostrato nella figura 2. Il calcolo dell'energia libera dello stato eccitato utilizzando questi valori di parametro ha prodotto un valore di 25.700 ^cm-1.

L'analisi del colore dello spettro delle basse temperature ha prodotto i seguenti risultati: coordinate di cromaticità = [0.15819, 0.03349], coordinate CIE = [0.19571, 0.041432, 1] e valore RGB previsto = [67, 0, 233]. I valori ottenuti per lo spettro della temperatura ambiente erano molto simili a quelli dello spettro delle basse temperature con differenze di colore impercettibili.

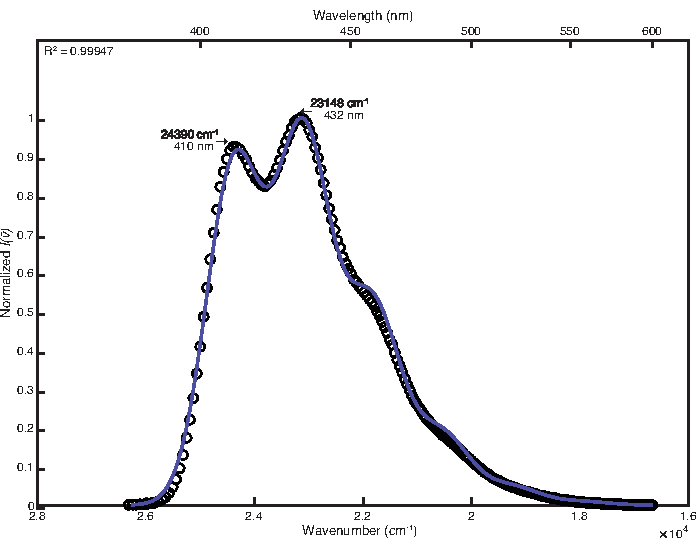
Figura 1: Adattamento monomodale del 9,10-difenilantracene (292 K): Questa figura mostra lo spettro di emissione a temperatura ambiente del 9,10-difenilantracene e la sua funzione di adattamento FCLSA, ottenuta attraverso l'ottimizzazione dei minimi quadrati seguita dalla regolazione manuale dei valori dei parametri. Questo è un esempio di uno spettro vagamente strutturato. Fare clic qui per visualizzare una versione ingrandita di questa figura.

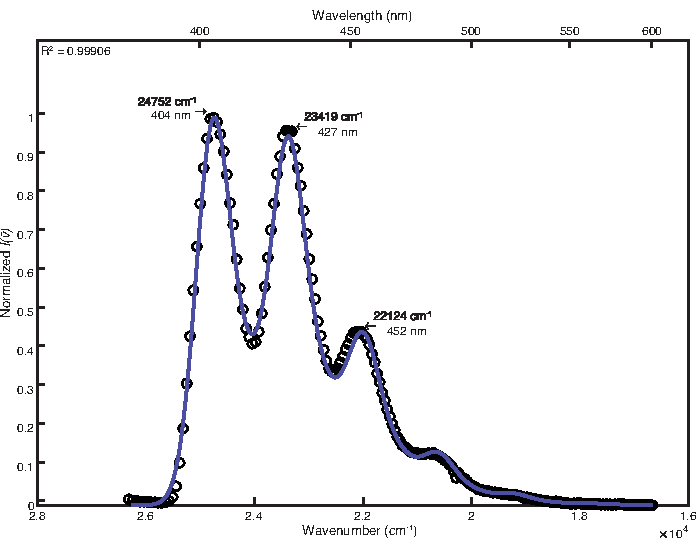
Figura 2: Doppia modalità di adattamento del 9,10-difenilantracene (77 K): Questa figura mostra lo spettro di emissione a bassa temperatura del 9,10-difenilantracene e la sua funzione di adattamento FCLSA, ottenuta attraverso un'ottimizzazione simplex. Questo è un esempio di spettro altamente strutturato. Fare clic qui per visualizzare una versione ingrandita di questa figura.

Discussione

Questa applicazione fornisce un'analisi facile e rapida degli spettri di emissione attraverso due metodi principali comunemente usati nella comunità fotofisica. Il primo è Franck-Condon Lineshape Analysis (FCLSA), che fornisce informazioni sull'energia e sull'accoppiamento vibronico associato al decadimento delle molecole di stato eccitato nei loro stati fondamentali. Ciò si ottiene ottimizzando i valori dei parametri per massimizzare la bontà di adattamento di uno spettro utilizzando una delle due possibili equazioni di modellazione FCLSA. Il secondo metodo di analisi fornisce informazioni sul colore osservato della luce emessa dalla molecola. Combinando le curve di colore tristimolo con i dati di intensità forniti, è possibile calcolare le coordinate CIE. Questa determinazione consente la previsione del colore estremamente accurata sia degli spettri di assorbimento che di emissione.

Gli spettri sperimentali di fotoluminescenza sono comunemente misurati utilizzando un tubo fotomoltiplicatore (PMT) o un dispositivo ad accoppiamento di carica (CCD) come rivelatore e tracciati come intensità di emissione rispetto alla lunghezza d'onda (nm). Molte caratterizzazioni fotofisiche, tra cui FCLSA e il calcolo dell'energia libera dello stato eccitato, sono eseguite nello spazio dei numeri d'onda, come dimostrato dall'uso di (^cm-1) nelle corrispondenti equazioni di 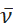cui sopra. Oltre alla conversione dell'asse x, l'intensità di emissione misurata rispetto alla lunghezza d'onda, indicata come I(λ) deve essere convertita in 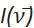. Questa applicazione identifica automaticamente le unità originali dell'asse x dei dati spettrali importati come lunghezza d'onda (nm) o numero d'onda (^cm-1). Per impostazione predefinita, l'applicazione converte quindi i dati spettrali, normalizza lo spettro in unità al picco di intensità massima e traccia lo spettro come "Normalizzato 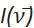vs. numero d'onda (^cm-1)" per indicare che è stata applicata la conversione di intensità corretta. Sebbene si raccomandi di eseguire tutti i raccordi utilizzando unità di numero d'onda, l'applicazione può anche tracciare lo spettro come "Normalizzato I(λ) vs. lunghezza d'onda (nm)" seguendo le istruzioni nella sezione 2 sopra.

Sono disponibili due algoritmi di ottimizzazione per l'utilizzo nell'applicazione. L'opzione predefinita è smorzato dei minimi quadrati, che utilizza l'algoritmo di Levenberg-Marquardt²¹. Combinando una versione della discesa del gradiente e l'algoritmo di Gauss-Newton, questo algoritmo trova minimi locali, non necessariamente globali. Sebbene questa sia una limitazione significativa, l'algoritmo offre vantaggi nella sua personalizzazione: questo metodo può tenere conto della ponderazione preferenziale dei punti dati, eseguire un adattamento robusto e visualizzare statistiche avanzate sulla bontà dell'adattamento²². Il metodo alternativo di ottimizzazione è privo di derivate, alimentato dall'algoritmo del simplesso di Nelder-Mead²³. Questo algoritmo utilizza un metodo euristico per restituire un minimo globale della funzione di costo data (in questo caso, una somma di differenze al quadrato tra le intensità previste e osservate). Il metodo simplex è stato utilizzato per FCLSA in precedenza, sebbene il codice che lo implementa non sia mai stato pubblicato²⁴.

Entrambi i metodi di ottimizzazione dei minimi quadrati e simplessi funzionano meglio per spettri strutturati che mostrano picchi stretti, ben definiti e simmetrici. Man mano che gli spettri diventano meno strutturati, il che significa che perdono simmetria e i picchi si allargano, questi metodi portano a adattamenti meno robusti in cui i parametri possono diventare altamente correlati. Tipicamente, gli spettri registrati a basse temperature o in mezzi rigidi sono più strutturati rispetto a quelli ottenuti vicino alla temperatura ambiente o in soluzione fluida 12,25,26. Le opzioni di adattamento robuste incluse nel metodo dei minimi quadrati possono aiutare ad alleviare questo problema. Questo problema può essere significativamente ridotto se uno o più parametri sono fissati su un valore costante durante l'ottimizzazione. Ad esempio, gli esperimenti di spettroscopia IR possono essere utilizzati per determinare i valori rilevanti di spaziatura quantistica (ħω). In alternativa, è possibile utilizzare i valori della letteratura pertinente per impostare limiti personalizzati per i parametri.

In alcuni casi, l'adattamento FCLSA e i parametri ottenuti dalle routine di ottimizzazione non rappresentano adeguatamente i dati anche quando vengono utilizzate opzioni di adattamento robuste o parametri fissi. Questo è un errore degli algoritmi di fitting e può essere associato ai parametri di adattamento FCLSA multipli (potenziale sovraparametrizzazione) o alla forma spettrale dei dati (spettri senza caratteristiche). In questi casi, un ulteriore miglioramento degli adattamenti può essere ottenuto utilizzando un "adattamento manuale" dei dati con manipolazione dei parametri FCLSA. L'adeguatezza di tali adattamenti può essere valutata visivamente e quantificata confrontando le statistiche sulla bontà dell'adattamento che vengono automaticamente incluse nel grafico.

Una routine generale da seguire per un adattamento accurato a mano consiste nei seguenti cinque passaggi: in primo luogo, determinare una stima iniziale per E₀ manualmente o automaticamente utilizzando uno dei tre metodi forniti. Per impostazione predefinita, il valore del parametro viene assegnato al numero d'onda associato al picco di intensità più elevato rilevato durante l'importazione dei dati. In alternativa, l'utente può definire E₀ come il numero d'onda al quale lo spettro di emissione interseca il suo corrispondente spettro di eccitazione. Il metodo finale per determinare E₀ utilizza la cosiddetta regola X%, dove X = 1 o 10. In questo metodo, E₀ è assegnato a un numero d'onda X% dell'intera larghezza a metà massima (FWHM) del picco di dati più prominente assumendo una forma a banda gaussiana. Il secondo passo nel protocollo di adattamento manuale è calcolare ħω in base alla spaziatura quantistica osservata nella struttura dello spettro di emissione. Se possibile, fare riferimento allo spettro IR della molecola e cercare di correlare il valore basato sulla fotoluminescenza a una banda forte nello spettro IR. In terzo luogo, determinare S in base alle intensità relative dei picchi spettrali. In quarto luogo, determinare un Δ v_1/2 approssimativo in base alla larghezza di banda. In quinto luogo, regolare iterativamente S e Δv_1/2 secondo necessità.

La difficoltà di eseguire FCLSA utilizzando spettri ampi e relativamente privi di caratteristiche è stata dimostrata attraverso la procedura di adattamento per 9,10-difenilantracene in soluzione fluida a 292 K rispetto a quella eseguita per lo spettro più strutturato ottenuto in vetro congelato a 77 K. Durante l'adattamento dello spettro della temperatura ambiente, l'ottimizzazione ha restituito un coefficiente iniziale di determinazione di 0,9971 che è stato migliorato a 0,9994 attraverso la regolazione manuale dei parametri e l'ispezione visiva dei risultati. Al contrario, il montaggio manuale della variante a bassa temperatura non era necessario a causa della struttura fine dello spettro che risultava in un coefficiente di determinazione pari a 0,9991 dopo l'ottimizzazione del simplesso.

In molti casi, entrambe le routine di ottimizzazione (minimi quadrati e simplex) restituiscono risultati molto simili. Ciò è indicativo del fatto che hanno trovato un minimo globale per i parametri FCLSA. In generale, il metodo dei minimi quadrati tende ad essere più adatto ai dati rumorosi, non ben strutturati o contenenti molti punti dati vicini allo zero nelle code dello spettro. Al contrario, il metodo simplex tende a restituire adattamenti migliori rispetto al metodo dei minimi quadrati per i dati che sono ben strutturati e possiedono pochi punti anomali. In questi casi, il metodo simplesso richiede in genere una piccola pre-ottimizzazione manuale dei valori dei parametri e nessuna regolazione dopo l'ottimizzazione. Per quei casi in cui il rumore dei dati o la mancanza generale di struttura impediscono un adattamento di alta qualità utilizzando uno dei metodi di ottimizzazione forniti, si raccomanda di utilizzare il metodo di adattamento manuale (vedi sopra) senza successiva ottimizzazione.

Questa applicazione offre diversi vantaggi rispetto alle precedenti implementazioni di Franck-Condon Lineshape Analysis. Il primo e più importante vantaggio è che è gratuito, accessibile al pubblico e completamente trasparente. Ciò si ottiene pubblicando il codice su GitHub, fornendo l'accesso a chiunque disponga di un computer e di una connessione Internet (https://github.com/USArmyResearchLab/ARL_Spectral_Fitting). Non solo chiunque può accedere a questa applicazione, ma può anche visualizzare il codice sottostante. Ciò offre un'opportunità per il feedback e lo sviluppo provenienti dalla comunità. Un ulteriore vantaggio risiede nella facilità d'uso di questa applicazione. Non è richiesta alcuna conoscenza di base dell'informatica o dell'interazione della riga di comando. Piuttosto, questo software utilizza una semplice interfaccia utente grafica (GUI) che consente ai ricercatori di ogni provenienza di eseguire le analisi spettrali sopra descritte. Inoltre, questa applicazione fornisce all'utente molteplici opzioni per il controllo sui metodi di ottimizzazione e può essere utilizzata per determinare l'energia libera dello stato eccitato. Infine, il software calcola e riporta diversi valori di colore utili tra cui coordinate di cromaticità, coordinate CIE, RGB e codici colore esadecimali. Tutte queste analisi possono essere eseguite in pochi secondi, richiedendo solo che l'utente prema un pulsante.

Materiali

Name	Company	Catalog Number	Comments
ARL Spectral Fitting	Army Research Laboratory	v1.0	https://github.com/USArmyResearchLab/ARL_Spectral_Fitting/releases/tag/v1.0