Ajustement spectral ARL en tant qu’application pour augmenter les données spectrales via l’analyse de la forme de ligne Franck-Condon et l’analyse des couleurs

Résumé

Ce protocole introduit les analyses de forme de ligne Franck-Condon (FCLSA) des spectres d’émission et sert de tutoriel pour l’utilisation du logiciel ARL Spectral Fitting. Le logiciel open source fournit un moyen simple et intuitif d’effectuer une analyse avancée des spectres d’émission, y compris les calculs d’énergie à l’état excité, la détermination des coordonnées de couleur CIE et FCLSA.

Résumé

L’application ARL Spectral Fitting fournit une méthode gratuite, accessible au public et entièrement transparente pour effectuer l’analyse de la forme de ligne Franck-Condon (FCLSA) sur des données spectrales, en plus de la détermination des coordonnées de couleur CIE et du traitement spectral de base. Bien que certaines des fonctionnalités puissent être trouvées dans des logiciels commerciaux ou dans des programmes créés par des groupes de recherche universitaires, nous pensons que ARL Spectral Fitting est la seule application qui possède les trois attributs susmentionnés.

Ce programme est conçu comme une application autonome, basée sur une interface graphique, pour une utilisation par un chercheur de laboratoire moyen sans nécessiter de connaissances en codage ou de logiciel propriétaire. En plus de l’exécutable autonome hébergé sur ARL GitHub, les fichiers MATLAB associés sont disponibles pour une utilisation et un développement ultérieur.

FCLSA augmente l’information trouvée dans les spectres de luminescence, fournissant un aperçu significatif de la relation entre le sol et les états excités d’une espèce photoluminescente. Cet aperçu est obtenu en modélisant des spectres avec deux versions (modes) d’une équation caractérisées par quatre ou six paramètres, selon le mode utilisé. Une fois optimisée, la valeur de chacun de ces paramètres peut être utilisée pour mieux comprendre la molécule, ainsi que pour effectuer une analyse plus approfondie (par exemple, le contenu énergétique libre de la molécule à l’état excité). Cette application fournit des outils pour un ajustement facile à la main des données importées, ainsi que deux méthodes pour optimiser cet ajustement des moindres carrés amortis, alimenté par l’algorithme de Levenberg-Marquardt, et un ajustement sans dérivée utilisant l’algorithme simplex de Nelder-Mead. De plus, des estimations de la couleur de l’échantillon peuvent être effectuées et rapportées en coordonnées CIE et RVB.

Introduction

Les mesures de photoluminescence, comprenant à la fois des spectres de fluorescence et de phosphorescence, sont largement utilisées dans divers domaines universitaires et applications industrielles¹. Les photocatalyseurs sont de plus en plus utilisés en synthèse organique pour la production de molécules cibles complexes et précieuses ^2,3,4. Afin de déterminer l’énergie des photocatalyseurs, l’énergie de l’état excité est régulièrement estimée à l’aide de spectres d’émission. Le développement de nouveaux matériaux d’éclairage, tels que les luminophores à diodes électroluminescentes organiques (OLED), nécessite que la sortie de couleur observée soit caractérisée et rapportée ^5,6. Les coordonnées colorimétriques de la Commission internationale de l’éclairage (CIE) sont couramment utilisées à cette fin⁷.

Le but de l’application ARL Spectral Fitting est de fournir une méthode rapide et facile pour augmenter les données spectrales grâce à une analyse significative qui est largement accessible à la fois en termes de facilité d’utilisation et de disponibilité (https://github.com/USArmyResearchLab/ARL_Spectral_Fitting). Ce logiciel exécute automatiquement plusieurs fonctions de traitement spectral de routine pour l’utilisateur, y compris la normalisation des données et la conversion entre la longueur d’onde, λ et le nombre d’onde, 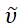, unités avec une échelle d’intensité appropriée comme indiqué dans l’équation ci-dessous¹. Le logiciel est capable de gérer une variété de formats de fichiers d’entrée et de sortie. Plusieurs analyses avancées sont facilement effectuées à l’aide du logiciel telles que le calcul des coordonnées CIE et chromatique, la prédiction des couleurs, la détermination de l’énergie libre à l’état excité (ΔG_ES) dans diverses unités, et FCLSA pour la détermination des paramètres FCLSA⁸.

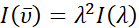
Une application basée sur une interface utilisateur graphique (GUI) a été recherchée parce qu’elle permet à tout chercheur d’effectuer cette analyse et ne nécessite aucune connaissance de base en informatique. Cette application a été écrite en MATLAB, à l’aide de son outil App Designer. En dehors d’ARL Spectral Fitting, il est pratiquement impossible de trouver une implémentation accessible au public d’une application conçue pour effectuer l’analyse de la forme de ligne Franck-Condon. En effet, les groupes de recherche ne publient pas leurs implémentations, préférant les garder propriétaires.

L’analyse de la forme de la ligne Franck-Condon (FCLSA) est souvent utilisée dans la caractérisation photophysique de nouveaux composés en raison de la richesse des informations qu’elle transmet sur la molécule 9,10,11,12,13,14. Chacun des quatre paramètres (six si en mode double) donne des informations sur l’état excité de la molécule. La quantité d’énergie, ou écart d’énergie 0-0, (E₀) est la différence entre les niveaux d’énergie zéro du sol et les états excités de la molécule. La largeur totale à la moitié du maximum (Δv_1/2)  renseigne sur les largeurs des lignes vibroniques individuelles. La constante de couplage électron-vibrationnel, ou facteur de Huang-Rhys, (S) est un calcul sans dimension basé sur le déplacement d’équilibre entre les états fondamental et excité de la molécule¹⁵. Enfin, le paramètre d’espacement quantique (ħω) est la distance entre les modes vibratoires qui régissent la désintégration non radiative d’une molécule.

Les équations pour le FCLSA en mode simple et double sont les suivantes :

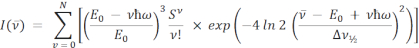
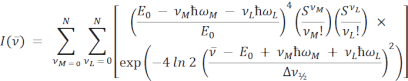
où les paramètres sont tels que définis précédemment. Dans l’équation du mode double, S et ħω sont séparés en termes d’énergie moyenne (_M) et faible (_L). 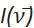est l’intensité au nombre d’onde V^10,16,17,18. Dans les deux équations, la sommation est effectuée sur N niveaux quantiques avec une valeur par défaut de N = 5, comme c’est couramment utilisé dans la littérature¹¹, mais n’importe quel entier peut être spécifié dans le logiciel d’ajustement spectral ARL sous Paramètres | En forme.

Protocole

1. Importation de données

1. Pour importer des données, appuyez sur le bouton Importer des données . Sélectionnez le type de spectre importé - excitation ou émission.
   1. Une fois le type de spectre choisi, assurez-vous que l’explorateur de fichiers MATLAB apparaîtra. Dans cette fenêtre, sélectionnez le fichier souhaité et appuyez sur Ouvrir. Les types de fichiers pris en charge incluent .TXT, . CSV, .XLS et . .XLSX.
      Remarque : Certains traitements de données sont effectués automatiquement avant de tracer les données importées. Cela comprend : la détection des unités de l’axe des x (nombre d’onde ou longueur d’onde) et la conversion en nombre d’onde, le cas échéant; normalisation de l’intensité du pic le plus élevé à 1; calcul de la quantité d’énergie, le cas échéant; et l’estimation de l’espacement quantique. Ces valeurs sont calculées en fonction des pics de données détectés avec la quantité d’énergie attribuée à la valeur du nombre d’onde du pic d’énergie le plus élevé et l’espacement quantique basé sur la distance moyenne entre les pics vicinaux, ce qui nécessite la détection d’au moins deux pics.
2. Pour charger l’un des spectres d’échantillons préemballés, appuyez sur le bouton correspondant au spectre souhaité, situé sous Info | Spectres d’échantillons. Neuf spectres d’échantillons sont livrés pré-emballés avec l’application.
3. Pour charger et tracer plusieurs spectres à la fois, activez la case à cocher Autoriser plusieurs spectres de données sur les axes sous Paramètres | | général Paramètres de la figure.
4. Pour sélectionner un spectre chargé différent de celui actuellement actif, appuyez sur le bouton Sélectionner le spectre à ajuster , puis choisissez le spectre souhaité dans la liste affichée dans le panneau Sélectionner un spectre nouvellement visible.

2. Traitement des données

REMARQUE: L’utilisateur peut souhaiter effectuer le traitement des données avant le processus d’ajustement. Les processus disponibles sont les suivants :

1. Sélection d’un pic devant servir de base à la normalisation : Pour sélectionner un pic qui servira de base à la normalisation de l’intensité, appuyez sur le bouton Sélectionner un pic pour la normalisation situé sous Paramètres | Généralités. Suivez les instructions affichées à l’écran. Le pic par défaut pour la normalisation de l’intensité est le pic d’intensité le plus élevé détecté lors de l’importation.
2. Conversion entre les unités de l’axe des x : pour convertir les unités de l’axe des x entre le nombre d’onde (^cm-1) et la longueur d’onde (nm), basculez le curseur situé sous Paramètres | Axe X vers le mode souhaité (nombre d’onde ou longueur d’onde). L’intensité ainsi que les unités de l’axe des x seront ajustées pour tous les spectres chargés, en utilisant l’équation donnée ci-dessus.
3. Limitation de la plage d’axes x : pour contraindre manuellement la plage d’axes x, sélectionnez Ajuster manuellement l’axe X et ajuster les limites sous Paramètres | Axe X. Ensuite, utilisez les contrôles révélés pour spécifier la plage d’axes x. Par défaut, l’application étend et contracte automatiquement la plage d’axes x pour s’adapter à tous les points de données chargés.
4. Méthodes de calcul de la variante E₀ : Pour sélectionner une autre méthode de calcul pour la quantité d’énergie, sélectionnez la méthode souhaitée sous Paramètres | En forme. La méthode par défaut est Full FCLSA fit. Pour passer à une autre méthode, sélectionnez le bouton radial correspondant et suivez les instructions à l’écran¹⁹.

3. Montage manuel

REMARQUE: En fonction de la quantité de structure visible dans le spectre, il peut être très avantageux d’initialiser les paramètres d’ajustement avec des estimations appropriées avant l’optimisation. Cette initialisation peut réduire le temps requis pour l’optimisation et permet de s’assurer que les valeurs retournées par l’optimisation sont réalistes pour le spectre.

1. Tracez la fonction d’ajustement avec ses valeurs de paramètre actuelles en appuyant sur le bouton Fonction d’ajustement du tracé .
2. À l’aide d’une combinaison de boutons de réglage grossiers et fins, de curseurs et de champs d’édition, ajustez les valeurs des paramètres pour augmenter la qualité de l’ajustement des données chargées. Par défaut, le coefficient de détermination (R²) est affiché dans le coin supérieur gauche du graphique. Utilisez-le comme mesure quantitative de la qualité de l’ajustement pour guider le choix des valeurs des paramètres.
   REMARQUE : Étant donné que la quantité d’énergie (E₀) et l’espacement quantique (ħω) sont calculés par l’application lors de l’importation des données, il est recommandé de maintenir ces valeurs constantes ou de varier le moins possible lors de l’ajustement manuel.
3. Par défaut, cette application utilise la formule d’analyse de ligne Franck-Condon monomode car elle est la plus pertinente pour les spectres de température ambiante. Si vous le souhaitez, par exemple lors de l’ajustement de spectres de 77 K, basculez entre le mode simple et le mode double dans Paramètres | En forme.
   Remarque : La surparamétrisation devient un problème plus important lors de l’ajustement en mode double par opposition au mode simple en raison du nombre accru de valeurs de paramètres flottant librement. Les spectres d’émission larges et sans structure posent le plus gros problème aux algorithmes d’ajustement et peuvent entraîner une corrélation croisée entre les paramètres FCLSA, en particulier entre Δv_1/2 et S. Lors de l’ajustement des spectres, il est impératif que les paramètres FCLSA obtenus soient vérifiés pour être physiquement réalistes en utilisant la priorité de la littérature comme guide.

4. Optimisation

1. Une fois que des paramètres initiaux satisfaisants ont été trouvés, une optimisation supplémentaire peut être effectuée. Pour ce faire, appuyez sur le bouton bleu Optimize Fit . L’optimisation exécutera et remplacera la fonction d’ajustement avec des valeurs de paramètres nouvellement optimisées.
2. Deux options d’optimisation sont proposées : les méthodes des moindres carrés et du simplexe. Pour basculer entre ces deux méthodes, basculez vers la méthode souhaitée dans Paramètres | Optimisation.
3. Si vous le souhaitez, personnalisez la méthode d’optimisation à l’aide des paramètres qui se trouvent sous Paramètres | Optimisation.
   Remarque : Afin de fournir à l’utilisateur le contrôle sur les routines d’optimisation, les options de personnalisation suivantes sont possibles pour les deux méthodes d’optimisation :
   1. Fixer les valeurs d’un paramètre : Pour fixer la valeur d’un paramètre lors de l’optimisation, appuyez sur la case à cocher dans le champ d’édition correspondant au paramètre souhaité.
   2. Délimitation personnalisée d’un paramètre pendant l’optimisation : pour afficher les options de délimitation personnalisée, activez la case à cocher Autoriser la délimitation des paramètres personnalisés pendant l’optimisation dans Paramètres | Optimisation. Pour spécifier des limites personnalisées pour la valeur d’un paramètre pendant l’optimisation, utilisez les contrôles révélés en appuyant sur le bouton Limites personnalisées sous le champ d’édition correspondant au paramètre souhaité.
   3. Déclencheurs de fin personnalisés pour l’optimisation : pour ajuster le nombre maximal d’itérations, la tolérance de terminaison sur la valeur du modèle ou la tolérance de terminaison sur les valeurs de coefficient, activez la case à cocher correspondante dans Paramètres | Optimisation et entrez la valeur souhaitée dans le champ d’édition correspondant.
      Remarque : les personnalisations suivantes sont disponibles uniquement pour l’optimisation des moindres carrés :
   4. Statistiques de qualité de l’ajustement : pour afficher les statistiques d’adéquation (coefficient de détermination ajusté du degré de liberté, somme des carrés dus à l’erreur, degrés de liberté de l’erreur et erreur quadratique moyenne) une fois l’optimisation terminée, activez la case à cocher située sous Paramètres | Optimisation.
   5. Options d’ajustement robuste : pour activer les options d’ajustement robuste, sélectionnez le menu souhaité dans la liste déroulante sous Paramètres | Optimisation. Par défaut, cette option est désactivée. Si vous le souhaitez, activez l’ajustement des moindres poids résiduels absolus ou des poids bicarrés, qui donnent moins de poids aux points de données aberrants.
   6. Pondération des données de seuil : Pour pondérer préférentiellement les points de données au-dessus d’une intensité seuil, choisissez une intensité qui servira de seuil et un multiplicateur de poids à appliquer à tous les points au-dessus de ce seuil. Par défaut, cette option est définie sur on, et le seuil et le multiplicateur de poids sont définis sur 0,1 et 1,2, respectivement. Ces options sont disponibles dans Paramètres | pondération des données.
   7. Pondération des données des extrèmes : Pour pondérer préférentiellement les points de données entourant les extrema locaux (pics et creux), sélectionnez le nombre de points de données entourant chaque extrémité à laquelle appliquer les pondérations préférentielles, ainsi que le multiplicateur de poids à appliquer pour ces points. Ces points sont plus riches en fonctionnalités car ils sont directement associés aux paramètres ajustés. Recherchez les paramètres de pondération des données extrema sous Paramètres | pondération des données qui est défini sur activé par défaut, et le nombre de points et le multiplicateur de poids sont définis sur 5 et 5, respectivement. Pour identifier visuellement les points de données utilisés dans la pondération préférentielle, sélectionnez Remplir les points de données saillants.

5. Calculs de chromaticité et d’énergie libre

1. Assurez-vous que l’ajustement optimisé des données et les valeurs de paramètres associées sont satisfaisants avant de procéder à des calculs supplémentaires. Pour effectuer ces calculs, appuyez sur le bouton Calculer , situé en bas du volet Calculs .
   REMARQUE: La première valeur renvoyée, étiquetée ΔG_ES (cm-1), est l’énergie libre de l’état excité calculée à l’aide de l’équation ^ci-dessous. L’unité par défaut pour cette valeur est l’inverse des centimètres (^cm-1), mais des unités d’électronvolt (eV) et de joule (J) sont également disponibles. Le calcul de l’énergie libre de l’état excité est donné par l’équation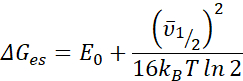
   
   1. Pour modifier l’unité, sélectionnez l’option souhaitée dans la zone de liste déroulante située sous Paramètres | Calculs. Cette valeur est déterminée en fonction de la quantité d’énergie (E₀), de la pleine largeur à demi-max (Δv_1/2), de la constante de Boltzmann (k_B) et de la température ambiante de l’expérience (T). La valeur de la température expérimentale est supposée être de 298 K mais peut être spécifiée comme 77 K ou toute autre température²⁰.
      1. Pour modifier la température expérimentale, choisissez l’option souhaitée sous Paramètres | Calculs | température expérimentale.
         REMARQUE : La deuxième valeur renvoyée est la coordonnée chromatique CIE, calculée à partir du spectre actuellement sélectionné. Lorsqu’elle est tracée sur un diagramme de chromaticité, cette valeur montre la couleur prédite du spectre de données actif.
   2. Pour afficher le diagramme de chromaticité avec les coordonnées tracées, appuyez sur le bouton contextuel (représenté par un carré avec une flèche pointant vers le coin supérieur droit) en regard de la zone de texte Coordonnées chromatiques .
   3. Pour vérifier la couleur prévue de l’échantillon, utilisez le troisième calcul, représenté par un rectangle coloré. Cette estimation est basée sur le même calcul qui a donné la coordonnée chromatique. Par défaut, l’illuminant standard CIE D65 est utilisé pour faire cette prédiction. Pour changer l’illuminant, sélectionnez l’option souhaitée dans le menu déroulant intitulée Point blanc dans Paramètres | Calculs.
2. Pour calculer les coordonnées chromatiques CIE et les valeurs de couleur pour plusieurs spectres chargés simultanément, activez la case à cocher correspondante située sous Paramètres | Calculs.
   Remarque : Ce paramètre est activé par défaut. Une fois qu’un deuxième spectre est tracé, l’icône sur le bouton contextuel à côté de l’étiquette de coordonnées chromatiques passera du carré avec une flèche pointant vers le coin supérieur droit à trois points (· · ·).
   1. Appuyez sur le bouton · · · pour afficher un panneau intitulé Sélectionner des spectres. Sélectionnez les spectres souhaités dans ce panneau et choisissez d’exporter les valeurs sous forme de tableau et/ou de diagramme d’affichage pour afficher le diagramme de chromaticité avec toutes les coordonnées tracées et étiquetées.

6. Exportation des données

1. Encore une fois, assurez-vous que l’ajustement des données chargées est satisfaisant et que tous les calculs souhaités ont été effectués. Pour exporter à la fois des données chargées et calculées, appuyez sur le bouton Exporter les données . Il existe six options d’exportation de données : Figure, Valeurs des paramètres, Points de données du spectre, Points de données d’ajustement, Valeurs de couleur et Diagramme de chromaticité.
   1. Pour exporter le tracé affiché en tant que figure préformatée pour la publication ou la présentation, sélectionnez Figure. Cette mise en forme peut être désactivée sous Paramètres | Paramètres généraux | Figure. Les types de fichiers pris en charge sont les suivants : . EPS (fichier vectoriel-graphic), .JPG, .PNG et .PDF.
   2. Pour exporter toutes les valeurs de paramètre, avec ou sans valeurs calculées, sous forme de table, sélectionnez Valeurs des paramètres. L’inclusion des valeurs calculées est basculable sous Paramètres | Calculs et les types de fichiers pris en charge sont . CSV, .TXT, . DAT, .XLS et . .XLSX.
   3. Pour exporter les données du spectre actuellement sélectionné sous la forme d’une série de points de données x-y, sélectionnez Points de données du spectre. Les valeurs X utiliseront des unités de nombre d’onde (^cm-1) ou de longueur d’onde (nm), selon la façon dont le graphique est défini via les paramètres. Les types de fichiers pris en charge sont les mêmes que ci-dessus dans la version 6.1.2.
   4. Pour exporter l’ajustement sous la forme d’une série de points de données x-y, toujours en fonction du mode actuel des axes, sélectionnez Ajuster les points de données. Les types de fichiers pris en charge sont les mêmes que ci-dessus dans la version 6.1.2.
   5. Pour exporter la chromaticité et les coordonnées CIE ainsi que la couleur prévue sous forme de valeur RVB, si cette option est activée, sélectionnez Valeurs de couleur. Les types de fichiers pris en charge sont les mêmes que ci-dessus dans la version 6.1.2.
   6. Pour exporter le diagramme de chromaticité avec les coordonnées chromatiques tracées associées au spectre chargé, sélectionnez Diagramme de chromaticité. Les types de fichiers pris en charge sont . EPS, .JPG, .PNG et .PDF.

Résultats

En utilisant la routine d’ajustement décrite ci-dessus, l’analyse Franck-Condon Lineshape a été réalisée sur deux spectres préemballés avec l’application: les spectres d’émission à température ambiante (292 K) et à basse température (77 K) pour le 9,10-diphénylanthracène dissous dans le toluène. Les mesures ont été obtenues à l’aide d’un spectrofluoromètre avec des solutions fluides dans des cuvettes de 1 cm et d’un porte-cuvette standard pour les mesures à température ambiante. Les mesures à basse température ont été obtenues en immergeant des tubes RMN dans de l’azote liquide dans un dewar pour générer des échantillons de verre congelé. Tous les spectres ont été corrigés en fonction de la réponse du détecteur. Un ajustement à un seul mode était suffisant pour le spectre de température ambiante, tandis qu’un mode double a été utilisé pour modéliser le spectre de basse température. L’analyse des couleurs a été effectuée sur les deux spectres et a donné des estimations similaires.

Pour s’adapter au spectre de température ambiante, le réglage manuel a été utilisé après l’optimisation des moindres carrés avec des personnalisations par défaut. Les valeurs finales des paramètres obtenues étaient les suivantes : E₀ = 24380 cm-1, Δv 1_/2 = 1200 cm-1, S = 1,25, ħω = 1280 ^cm-1. Le coefficient de détermination calculé était de 0,99947, comme le montre la figure 1. Le calcul de l’énergie libre de l’état excité à l’aide de ces valeurs de paramètres a donné une valeur de 25 000 ^cm-1.

L’optimisation simplex a été utilisée pour s’adapter au spectre des basses températures. L’ajustement manuel n’était pas nécessaire après l’optimisation. Les valeurs finales des paramètres obtenues étaient les suivantes : E 0 = 24764 cm-1, Δv 1/2 = 746 cm-1, S 1= 1,13, ħω 1 = ₁₃₈₂ cm-1, S₂ = _0,31, ħω₂= 651 ^cm-1. Le coefficient de détermination calculé était de 0,9991, comme le montre la figure 2. Le calcul de l’énergie libre de l’état excité à l’aide de ces valeurs de paramètres a donné une valeur de 25 700 ^cm-1.

L’analyse des couleurs du spectre des basses températures a donné les résultats suivants : coordonnée chromatique = [0,15819, 0,03349], coordonnée CIE = [0,19571, 0,041432, 1] et valeur RVB prévue = [67, 0, 233]. Les valeurs obtenues pour le spectre de température ambiante étaient très similaires à celles du spectre de basse température avec des différences de couleur imperceptibles.

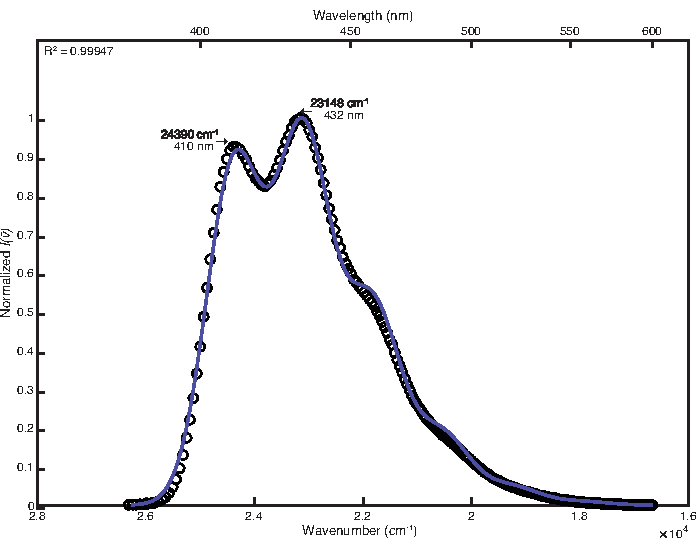
Figure 1 : Ajustement monomode du 9,10-diphénylanthracène (292 K) : Cette figure montre le spectre d’émission à température ambiante du 9,10-diphénylanthracène et sa fonction d’ajustement FCLSA, obtenue grâce à l’optimisation des moindres carrés suivie d’un ajustement manuel des valeurs des paramètres. C’est un exemple de spectre peu structuré. Veuillez cliquer ici pour voir une version agrandie de cette figure.

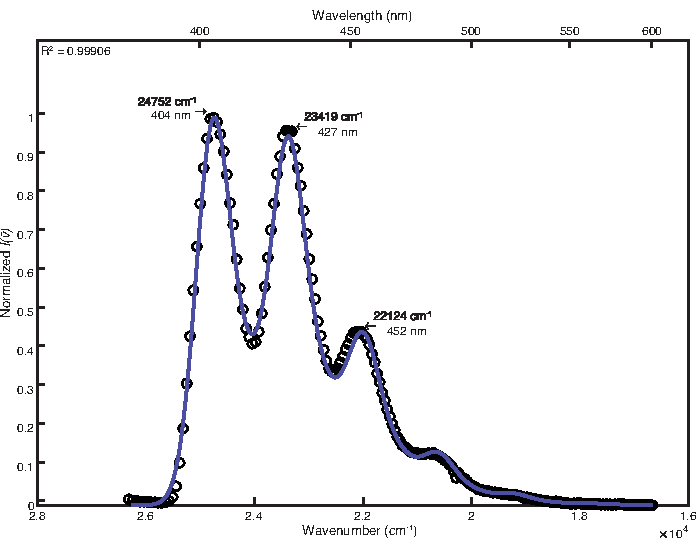
Figure 2 : Ajustement en mode double du 9,10-diphénylanthracène (77 K) : Cette figure montre le spectre d’émission à basse température du 9,10-diphénylanthracène et sa fonction d’ajustement FCLSA, obtenue grâce à une optimisation simplexe. C’est un exemple de spectre très structuré. Veuillez cliquer ici pour voir une version agrandie de cette figure.

Discussion

Cette application fournit une analyse facile et rapide des spectres d’émission grâce à deux méthodes principales couramment utilisées dans la communauté photophysique. Le premier est l’analyse de la forme de ligne Franck-Condon (FCLSA), qui donne un aperçu de l’énergie et du couplage vibronique associés à la désintégration des molécules excitées à leurs états fondamentaux. Ceci est réalisé en optimisant les valeurs des paramètres pour maximiser la qualité de l’ajustement d’un spectre à l’aide de l’une des deux équations de modélisation FCLSA possibles. La deuxième méthode d’analyse donne un aperçu de la couleur observée de la lumière émise par la molécule. En combinant des courbes de couleur tristimulus avec les données d’intensité fournies, la coordonnée CIE peut être calculée. Cette détermination permet une prédiction très précise des couleurs des spectres d’absorption et d’émission.

Les spectres de photoluminescence expérimentale sont généralement mesurés à l’aide d’un tube photomultiplicateur (PMT) ou d’un dispositif à couplage de charge (CCD) comme détecteur et tracés en fonction de l’intensité de l’émission en fonction de la longueur d’onde (nm). De nombreuses caractérisations photophysiques, y compris FCLSA et le calcul de l’énergie libre de l’état excité, sont effectuées dans l’espace des nombres d’onde, comme démontré par l’utilisation de 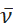(cm-1) dans les équations correspondantes ^ci-dessus. En plus de la conversion de l’axe des abscisses, l’intensité d’émission mesurée en fonction de la longueur d’onde, notée I(λ), doit être convertie en 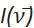. Cette application identifie automatiquement les unités originales de l’axe des x des données spectrales importées en tant que longueur d’onde (nm) ou nombre d’onde (^cm-1). Par défaut, l’application convertit ensuite les données spectrales, normalise le spectre en unité au pic d’intensité maximale et trace le spectre comme « Normalisé 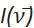vs nombre d’onde (^cm-1) » pour indiquer que la conversion d’intensité correcte a été appliquée. Bien qu’il soit recommandé que tous les ajustements soient effectués à l’aide d’unités de nombre d’onde, l’application peut également tracer le spectre comme « Normalisé I(λ ) vs longueur d’onde (nm) » en suivant les instructions de la section 2 ci-dessus.

Deux algorithmes d’optimisation peuvent être utilisés dans l’application. L’option par défaut est les moindres carrés amortis, qui utilisent l’algorithme de Levenberg-Marquardt²¹. En combinant une version de descente de gradient et l’algorithme de Gauss-Newton, cet algorithme trouve des minima locaux, pas nécessairement globaux. Bien qu’il s’agisse d’une limitation importante, l’algorithme offre des avantages dans sa personnalisation - cette méthode peut prendre en compte la pondération préférentielle des points de données, effectuer un ajustement robuste et afficher des statistiques avancées de qualité d’ajustement²². La méthode alternative d’optimisation est sans dérivée, alimentée par l’algorithme simplex de Nelder-Mead²³. Cet algorithme utilise une méthode heuristique pour renvoyer un minimum global de la fonction de coût donnée (dans ce cas, une somme de différences au carré entre les intensités prédites et observées). La méthode simplex a déjà été utilisée pour FCLSA, bien que le code l’implémentant n’ait jamais été publié²⁴.

Les méthodes d’optimisation des moindres carrés et du simplexe fonctionnent mieux pour les spectres structurés qui présentent des pics étroits, bien définis et symétriques. Au fur et à mesure que les spectres deviennent moins structurés, ce qui signifie qu’ils perdent leur symétrie et que les pics s’élargissent, ces méthodes conduisent à des ajustements moins robustes où les paramètres peuvent devenir fortement corrélés. Typiquement, les spectres enregistrés à basse température ou en milieu rigide sont plus structurés que ceux obtenus près de la température ambiante ou en solution fluide 12,25,26. Les options d’ajustement robustes incluses avec la méthode des moindres carrés peuvent aider à atténuer ce problème. Ce problème peut être considérablement diminué si un ou plusieurs des paramètres sont fixés à une valeur constante lors de l’optimisation. Par exemple, les expériences de spectroscopie IR peuvent être utilisées pour déterminer les valeurs pertinentes d’espacement quantique (ħω). Alternativement, les valeurs pertinentes de la littérature peuvent être utilisées pour définir des limites personnalisées pour les paramètres.

Dans certains cas, l’ajustement FCLSA et les paramètres obtenus à partir des routines d’optimisation ne représentent pas adéquatement les données, même lorsque des options d’ajustement robustes ou des paramètres fixes sont utilisés. Il s’agit d’un échec des algorithmes d’ajustement et peut être associé aux multiples paramètres d’ajustement FCLSA (surparamétrage potentiel) ou à la forme spectrale des données (spectres sans caractéristiques). Dans ces cas, une amélioration supplémentaire des ajustements peut être obtenue en utilisant un « ajustement manuel » des données avec manipulation des paramètres FCLSA. L’adéquation de ces ajustements peut être évaluée visuellement et quantifiée en comparant les statistiques de qualité de l’ajustement qui sont automatiquement incluses dans le graphique.

Une routine générale à suivre pour un ajustement manuel précis comprend les cinq étapes suivantes: Tout d’abord, déterminez une estimation initiale pour E₀ manuellement ou automatiquement en utilisant l’une des trois méthodes fournies. Par défaut, la valeur du paramètre est affectée au nombre d’onde associé au pic d’intensité le plus élevé détecté lors de l’importation des données. Alternativement, l’utilisateur peut définir E₀ comme le nombre d’onde auquel le spectre d’émission croise son spectre d’excitation correspondant. La méthode finale pour déterminer E₀ utilise la règle dite de X%, où X = 1 ou 10. Dans cette méthode, E₀ est affecté à un nombre d’onde X % de la largeur totale à l’intensité demi-maximale (FWHM) du pic de données le plus important en supposant une forme de bande gaussienne. La deuxième étape du protocole d’ajustement manuel consiste à calculer ħω en fonction de l’espacement quantique observé dans la structure du spectre d’émission. Si possible, référez-vous au spectre IR de la molécule et essayez de corréler la valeur basée sur la photoluminescence à une bande forte dans le spectre IR. Troisièmement, déterminez S en fonction des intensités relatives des pics spectraux. Quatrièmement, déterminez un Δv_1/2 approximatif en fonction de la bande passante. Cinquièmement, réajuster itérativement S et Δv_1/2 si nécessaire.

La difficulté d’effectuer des FCLSA à l’aide de spectres larges et relativement dépourvus de caractéristiques a été démontrée par la procédure d’ajustement du 9,10-diphénylanthracène en solution fluide à 292 K par rapport à celle effectuée pour le spectre plus structuré obtenu dans du verre congelé à 77 K. Lors de l’ajustement du spectre de température ambiante, l’optimisation a renvoyé un coefficient de détermination initial de 0,9971 qui a été amélioré à 0,9994 grâce au réglage manuel des paramètres et à l’inspection visuelle des résultats. En revanche, l’ajustement manuel de la variante basse température n’était pas nécessaire en raison de la structure fine du spectre qui a abouti à un coefficient de détermination égal à 0,9991 après optimisation simplexe.

Dans de nombreux cas, les deux routines d’optimisation (moindres carrés et simplex) renvoient des résultats très similaires. Cela indique qu’ils ont trouvé un minimum global pour les paramètres FCLSA. En général, la méthode des moindres carrés a tendance à être mieux adaptée aux données bruyantes, mal structurées ou contenant de nombreux points de données proches de zéro aux extrémités du spectre. Inversement, la méthode simplexe a tendance à renvoyer de meilleurs ajustements que la méthode des moindres carrés pour les données bien structurées et possédant peu de points aberrants. Dans ces cas, la méthode simplexe nécessite généralement peu de pré-optimisation manuelle des valeurs des paramètres et aucun ajustement après optimisation. Pour les cas où le bruit des données ou l’absence générale de structure empêche un ajustement de haute qualité en utilisant l’une ou l’autre des méthodes d’optimisation fournies, il est recommandé d’utiliser la méthode d’ajustement manuel (voir ci-dessus) sans optimisation ultérieure.

Cette application offre plusieurs avantages par rapport aux implémentations précédentes de Franck-Condon Lineshape Analysis. Le premier et le plus important avantage est qu’il est gratuit, accessible au public et totalement transparent. Ceci est accompli en publiant le code sur GitHub, fournissant un accès à toute personne disposant d’un ordinateur et d’une connexion Internet (https://github.com/USArmyResearchLab/ARL_Spectral_Fitting). Non seulement n’importe qui peut accéder à cette application, mais ils peuvent également afficher le code sous-jacent. Cela offre une occasion de rétroaction et de développement provenant de la communauté. Un avantage supplémentaire réside dans la facilité d’utilisation de cette application. Aucune connaissance de base de l’informatique ou de l’interaction en ligne de commande n’est requise. Ce logiciel utilise plutôt une interface utilisateur graphique (GUI) simple qui permet aux chercheurs de tous horizons d’effectuer les analyses spectrales décrites ci-dessus. En outre, cette application offre à l’utilisateur de multiples options pour le contrôle des méthodes d’optimisation et peut être utilisée pour déterminer l’énergie libre de l’état excité. Enfin, le logiciel calcule et rapporte plusieurs valeurs de couleur utiles, notamment les coordonnées chromatiques, les coordonnées CIE, RVB et les codes de couleur hexadécimaux. Toutes ces analyses peuvent être effectuées en quelques secondes, nécessitant seulement que l’utilisateur appuie sur un bouton.

matériels

Name	Company	Catalog Number	Comments
ARL Spectral Fitting	Army Research Laboratory	v1.0	https://github.com/USArmyResearchLab/ARL_Spectral_Fitting/releases/tag/v1.0