Elektrisches Potential
Quelle: Yong P. Chen, PhD, Department of Physics & Astronomie, College of Science, Purdue University, West Lafayette, IN
Elektrisches Potential, auch bekannt als "Spannung", misst die elektrische potentielle Energie pro Einheit berechnet. Elektrische Feld ist eine skalare Größe und ist für viele elektrische Effekte von grundlegender Bedeutung. Wie potentielle Energie ist was physikalisch sinnvolle der Unterschied des elektrischen Potenzials. Beispielsweise bezieht sich die räumliche Variation in das elektrische Potenzial auf das elektrische Feld, die Anlass für die elektrische Kraft auf eine Gebühr. Der Unterschied des elektrischen Potenzials zwischen zwei Punkten in einem Widerstand treibt den elektrischen Stromfluss.
Dieses Experiment wird ein Voltmeter und einer Leuchtstoffröhre verwenden, um das elektrische Potential (genauer gesagt, die Potentialdifferenz zwischen zwei Punkten im Raum) erzeugt durch eine geladene Kugel zu demonstrieren. Das Experiment zeigt das Konzept der Potentialausgleich Oberflächen, die senkrecht auf die elektrischen Felder sind.
Eine Punktladung Q befindet sich am Ursprung (R = 0) erzeugt eine elektrische Spannung:
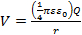 (Gleichung 1)
(Gleichung 1)
an jedem Punkt im Raum mit einem Abstand R von der Ladung (im Ursprung R = 0). Gleichung 1 beschreibt auch das elektrische Potential produziert durch eine gleichmäßig geladenen Kugel (zentriert auf R = 0) mit Gesamtladung Q in den Raum außerhalb der Sphäre (Abbildung 1). In beiden Fällen ist der "Bezugspunkt" (wobei das Potential Null ist) an den unendlich weit weg von der Ladung. Das elektrische Potenzial variiert entlang radialer Richtung, der die Richtung des elektrischen Feldes ist.
Für zwei Punkte P1 und P2 mit Abstand R1 und R2 vom Ursprung (Mitte der Ladung) bzw. ist die Potentialdifferenz zwischen diesen beiden Punkten:
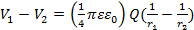 (Gleichung 2)
(Gleichung 2)
Punkt P2 im unendlichen (→∞) ist, reduziert diese Gleichung 2 nach Gleichung 1. Daher gibt es eine Potentialdifferenz zwischen zwei Punkten, wenn und nur wenn diese beiden Punkte einen unterschiedlichen Abstand vom Ursprung (Mitte der Ladung haben). Eine sphärische Fläche am Ursprung zentriert ist in diesem Fall eine "Potentialausgleich Oberfläche". Beachten Sie in diesem Fall das elektrische Feld (entlang der radialen Richtung) senkrecht zur Erdung Oberfläche (Sphäre). Dies erweist sich um in der Regel wahr zu sein: die Erdung Oberfläche ist senkrecht zur Richtung des elektrischen Feldes.

Abbildung 1: Schematische Darstellung einer geladenen Kugel mit einem elektrischen Generator verbunden. Ein Voltmeter wird verwendet, um das elektrische Potential an einem Punkt "A" (mit Abstand R vom Mittelpunkt der Kugel) zu messen.
1. elektrisches Potential aufgrund einer geladenen Kugel
- Erhalten Sie einen van der Graff-Generator, der kostenlos auf eine Metallkugel setzen kann. Der Mittelpunkt der Kugel ist definiert als der Ursprung für dieses Experiment.
- Erhalten Sie ein Voltmeter. Verbinden Sie (mit Durchführung von Kabeln) "−" terminal auf den Boden oder Referenz terminal am van der Graff Generator, oder eine Erdung (z. B. ein großes leitfähige Rohr) weit weg (mindestens ein paar Meter) vom Generator. Verbinden Sie die Klemme "+" mit einem Voltmeter Kabel mit einer Spannung Sondenspitze, die bewegt werden kann. Die schematische Verbindung ist in Abbildung 1dargestellt.
- Drehen Sie die Kurbel des Generators um mindestens 10 Umdrehungen, die Kugel zu berechnen.
- Mit dem Voltmeter eingeschaltet, setzen Sie die Spitze des Prüfpunkts Spannung (verbunden mit dem "+" Terminal das Voltmeter) ca. 0,5 m vom Ursprung. Verwenden Sie ein Lineal, Messen oder den Abstand vorher markieren, falls gewünscht. Notieren Sie die Spannung auf das Voltmeter lesen. Bewegen Sie die Spitze, aber halten Sie den Abstand vom Ursprung. Beobachten Sie das Voltmeter lesen.
- Wiederholen Sie den obigen Schritt mit der Spannung Sondenspitze bzw. ca. 1 m und 1,5 m platziert.
- Erhalten Sie ein Fluoreszenz-Rohr (Handheld). Bringen Sie das Rohr auf ca. 0,5 m Weg von der Mitte der geladenen Kugel ( Abb. 2a). Zunächst orientieren Sie das Rohr, so dass es in der radialen Richtung Weg von der Kugel. Beobachten Sie das Rohr (Schalten Sie die Lichter, die Beobachtung in relativer Dunkelheit zu erleichtern). Dann drehen Sie das Rohr um 90 Grad, so dass sie in radialer Richtung ( Abb. 2 b) senkrecht steht. Beobachten Sie das Rohr wieder.
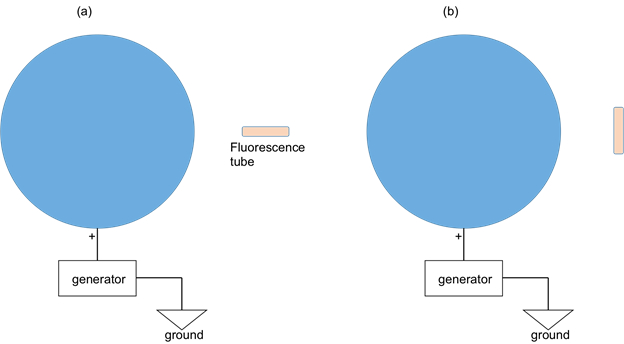
Abbildung 2: Schematische Darstellung einer geladenen Kugel mit einem elektrischen Generator verbunden. Eine Fluoreszenz-Röhre wird verwendet, um die Potentialdifferenz zwischen den beiden Enden des Rohres angeben. Im Falle von (a) das Rohr orientiert sich entlang der radialen Richtung; und (b) das Rohr wird orientierten senkrecht zur Radialrichtung.
In Schritten 1.4-1.5, das Voltmeter beobachtet werden, ähnlich wie Lesungen geben, wenn die Sondenspitze auf ähnliche Entfernungen vom Ursprung gehalten wird (d. h. auf eine Erdung Oberfläche). Allerdings sinkt die Spannung, wenn die Sonde weiter bewegt sich weg von der Herkunft. Die Spannung bei 1 m und 1,5 m Entfernung lesen werden ca. 1/2 und 1/3 der Lesung bei 0,5 m bzw.. Wenn die Spannung V gegen die inverse Distanz gemessen (1/R) aufgetragen, ergibt sich eine gerade Linie, erwartungsgemäß von Gleichung 1.
Elektrisches Potential (Spannung) ist allgegenwärtig und vielleicht die am häufigsten verwendeten Menge Strom. Es ist oft viel bequemer zu bedienen elektrisches Potential (das ist ein Skalar) als elektrisches Feld (das ist ein Vektor), obwohl die beiden miteinander verbunden werden können. Elektrische Potentialdifferenz wird Antriebs- und Steuerungstechnik kostenlos Bewegung (beschleunigen/verlangsamen/abzulenken-Gebühren), zum Beispiel in einem TV-Bildschirm oder Elektronenmikroskop. Elektrische Potentialdifferenz (was wir in der Regel Spannung nennen) treibt auch aktuelle Strömung in einem Leiter. Wann immer man eine Spannung misst, misst man die elektrische Potentialdifferenz zwischen zwei Punkten (von denen manchmal einen Bezugspunkt oder Boden definiert Nullpotential ist).
Der Autor des Experiments anerkennt die Unterstützung von Gary Hudson für die Vorbereitung des Materials und Chuanhsun Li für den Nachweis der Schritte in dem Video.
pringen zu...
Videos aus dieser Sammlung:

Now Playing
Elektrisches Potential
Physics II
104.3K Ansichten

Elektrische Felder
Physics II
77.4K Ansichten

Magnetische Felder
Physics II
33.3K Ansichten

Elektrische Ladung in einem Magnetfeld
Physics II
33.6K Ansichten

Ohmsches Gesetz
Physics II
26.2K Ansichten

Reihen- und Parallelwiderstände
Physics II
33.1K Ansichten

Kapazität
Physics II
43.7K Ansichten

Induktivität
Physics II
21.5K Ansichten

RC/RL/LC-Schaltungen
Physics II
142.7K Ansichten

Halbleiter
Physics II
29.6K Ansichten

Photoeffekt
Physics II
32.6K Ansichten

Reflexion und Brechung
Physics II
35.7K Ansichten

Interferenz und Beugung
Physics II
90.8K Ansichten

Stehende Wellen
Physics II
49.7K Ansichten

Schallwellen und Dopplereffekt
Physics II
23.4K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten